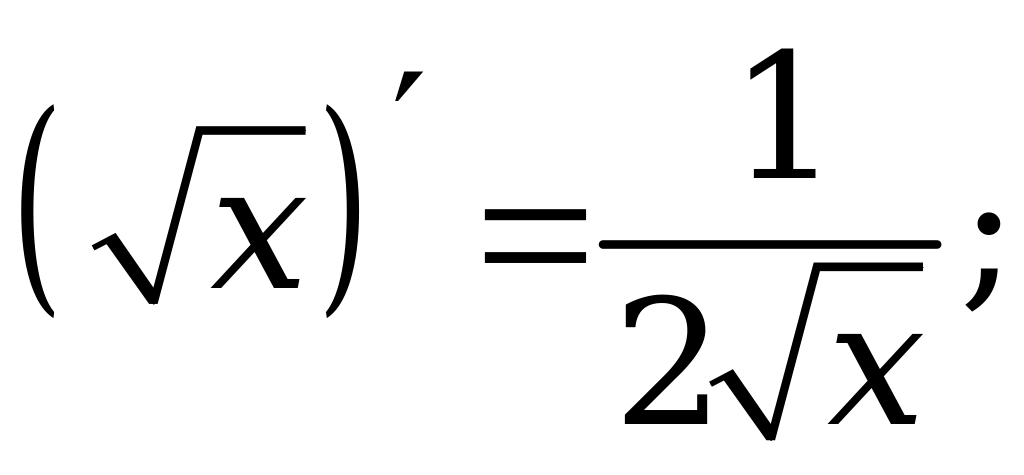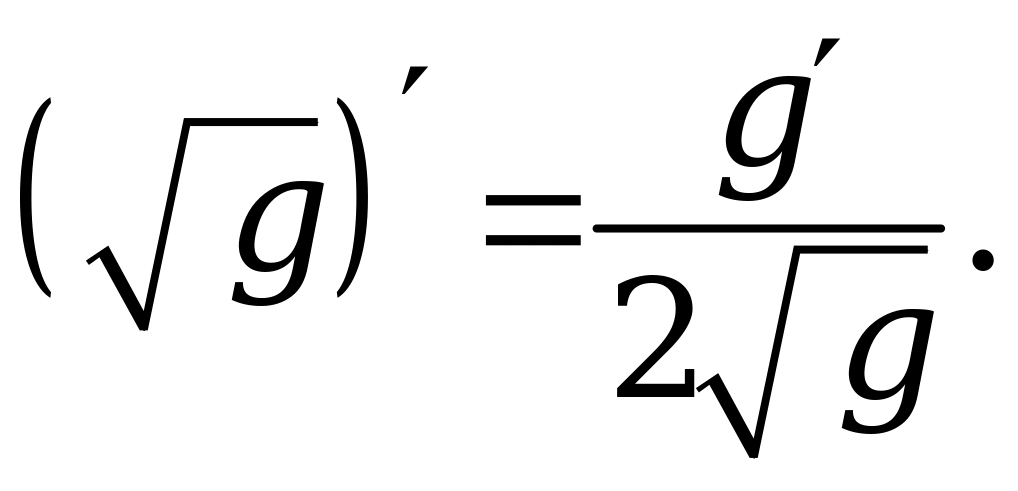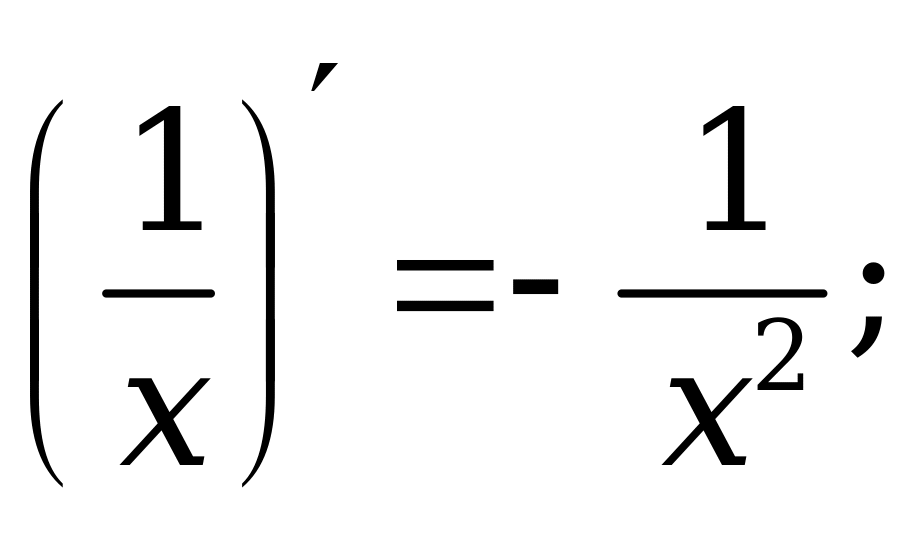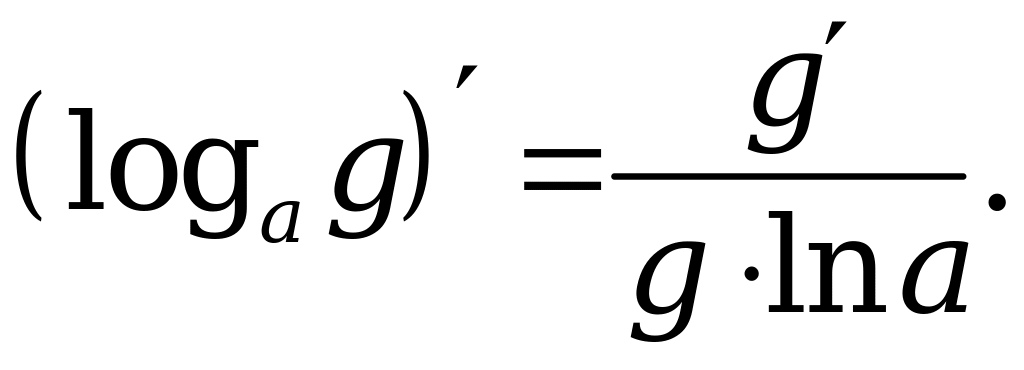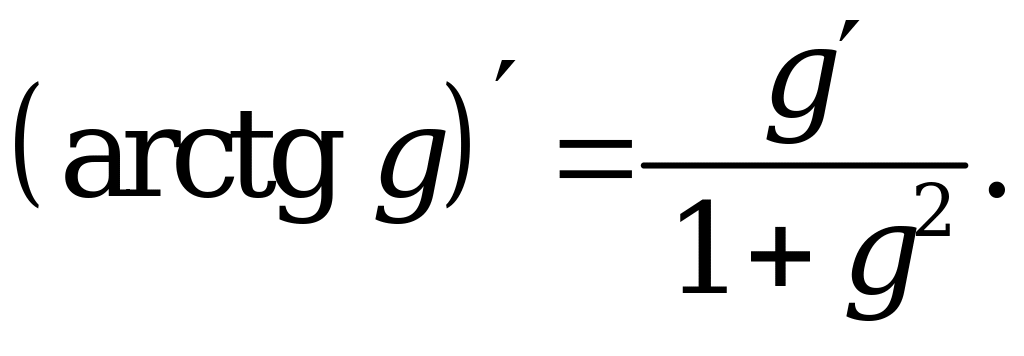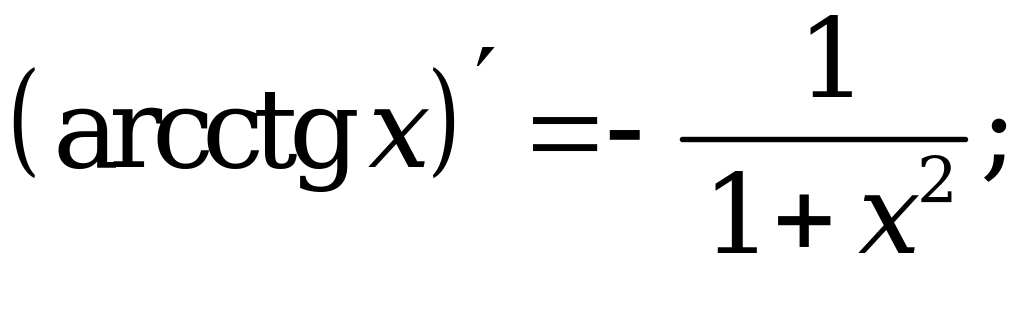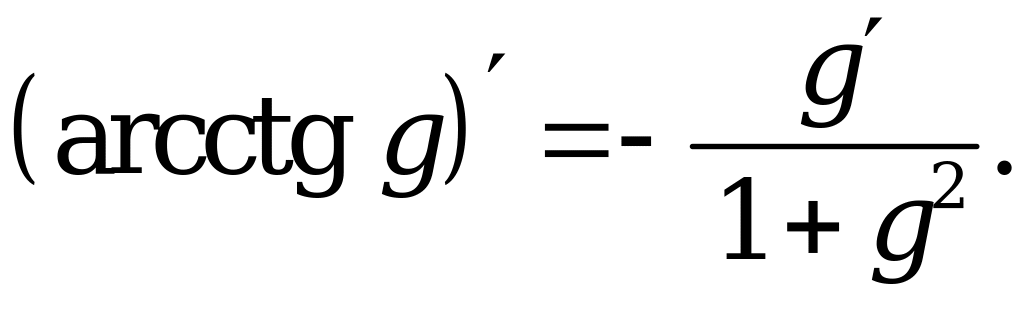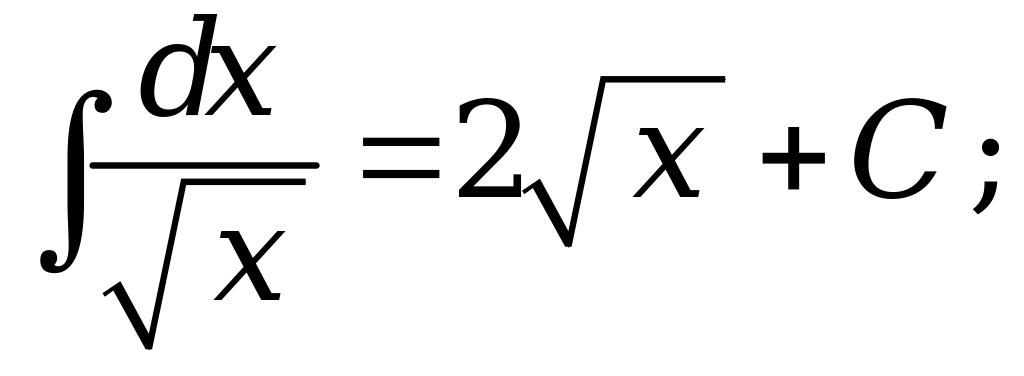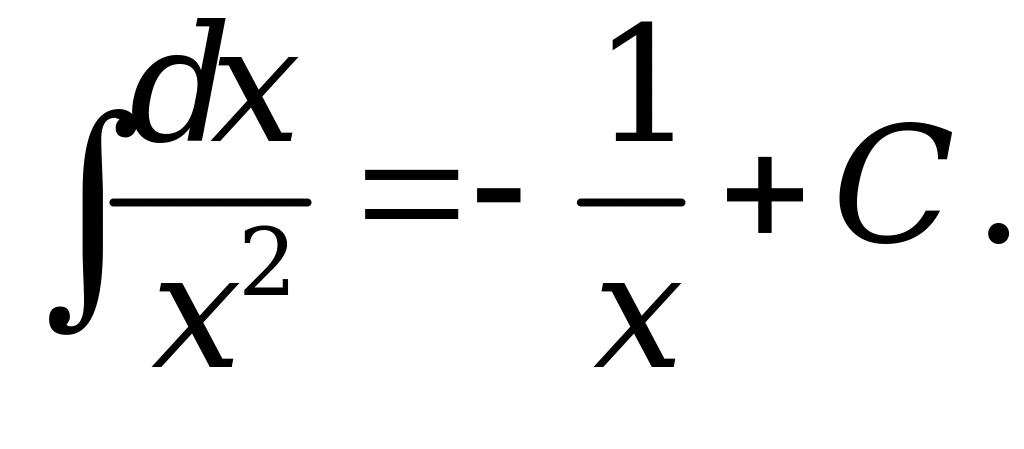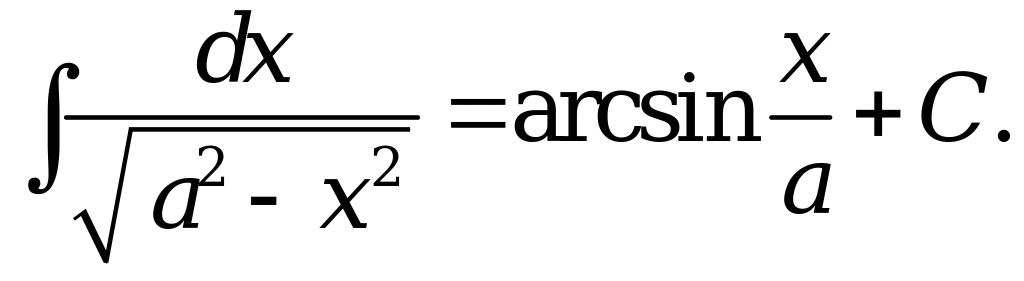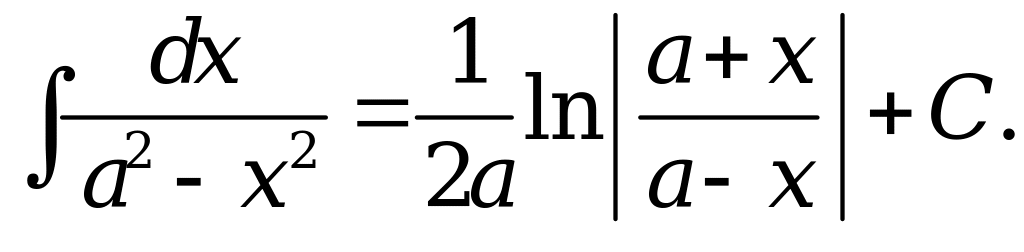m33751_10

Приложения

1. Используемые обозначения

– выражение А эквивалентно выражению B.

– из выражения А следует выражение B.

N – множество натуральных чисел .

R – множество действительных (вещественных) чисел.

e – основание натурального логарифма

– сумма .

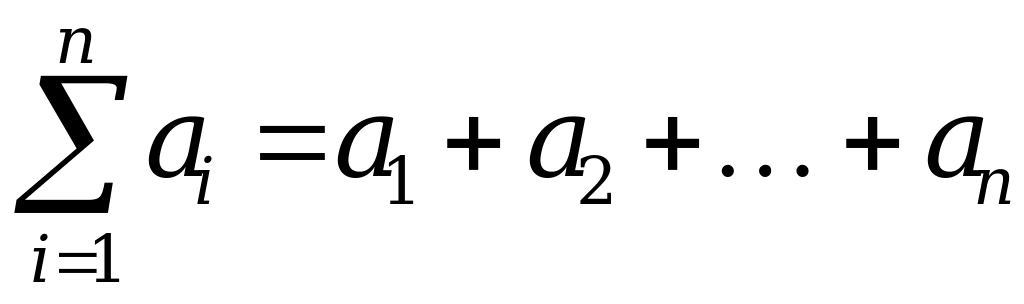2. Формулы сокращенного умножения

1. ;

2. ;

3. .

4. ;

5. ;

3. Дроби

1. ;	2. ;	3. ;
4. ;	5. ;	6. ;
7. ;	8. ;	9. .

4. Степени

Определение. Для , , ,

, , ,

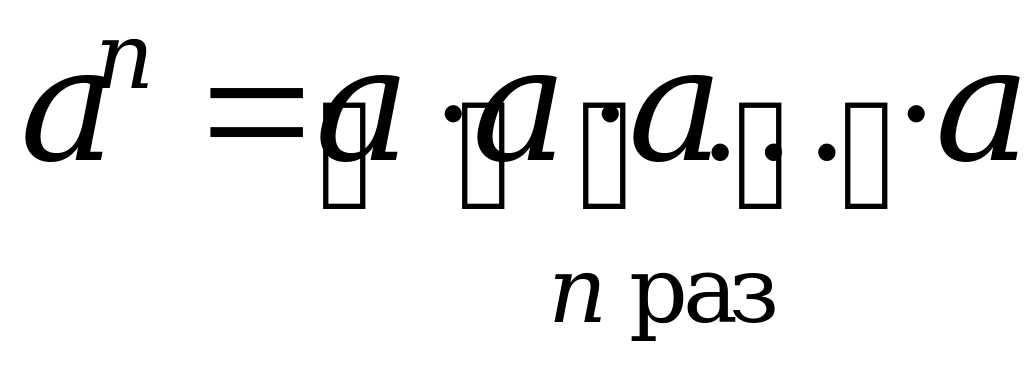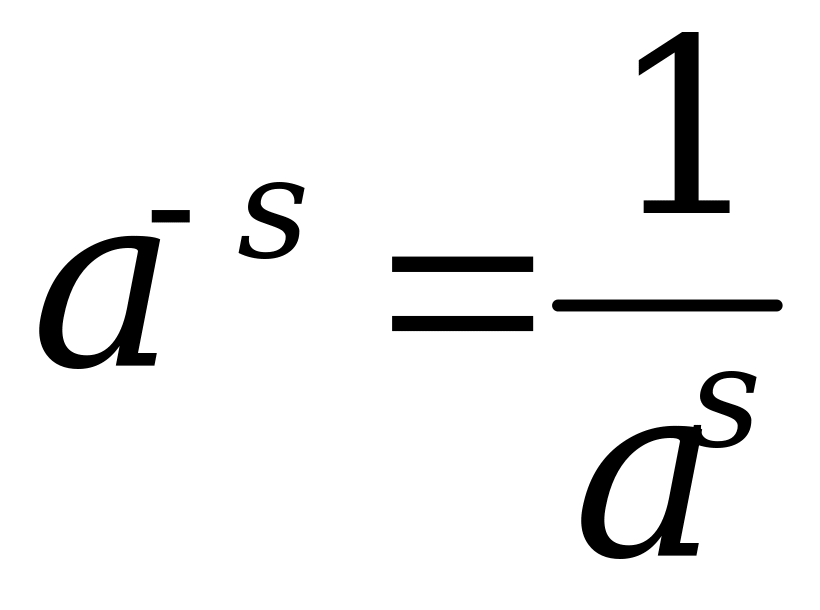где a – основание, n, s – показатель степени.

Свойства:

1. ;	2. ;	3. ;
4. ;	5. ;	6. ;
7. ;	8. ;	9. .

5. Формулы тригонометрии

1. ,	,	;
2. ,	,	;
3. ,	.

4. Некоторые значения тригонометрических функций

a			–1		0
					0
a		–1		0		1
				0

6. Решения простейших уравнений

1. Тригонометрические уравнения

Уравнение:	Решение:	Уравнение:	Решение:
,	;	,	;
,	;	,	.

2. Квадратное уравнение

Дискриминант:	,	,	,
;	;	;	.
Теорема Виета:	,	.

3. Показательное и логарифмическое уравнения (при , ).

Уравнение:	Решение:	Уравнение:	Решение:
	.

7. Основные правила
дифференцирования	и		интегрирования
1. .		6. .
2. .		7. .
3. .		8. .
4. .		9. .
5. .

8. Таблица производных основных
элементарных	и	сложных функций
1.
2.
3.
4.
5.
6.
7.
8.

9. Таблица основных неопределенных интегралов
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

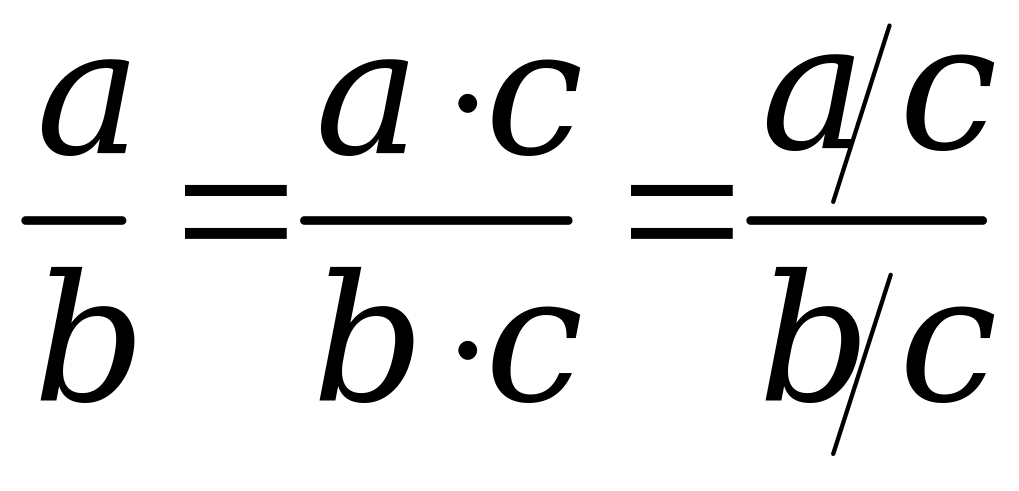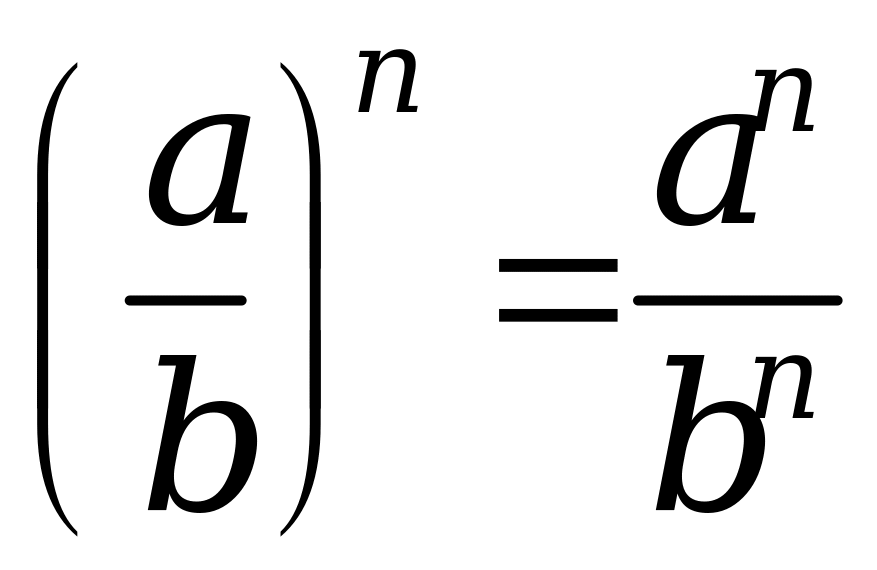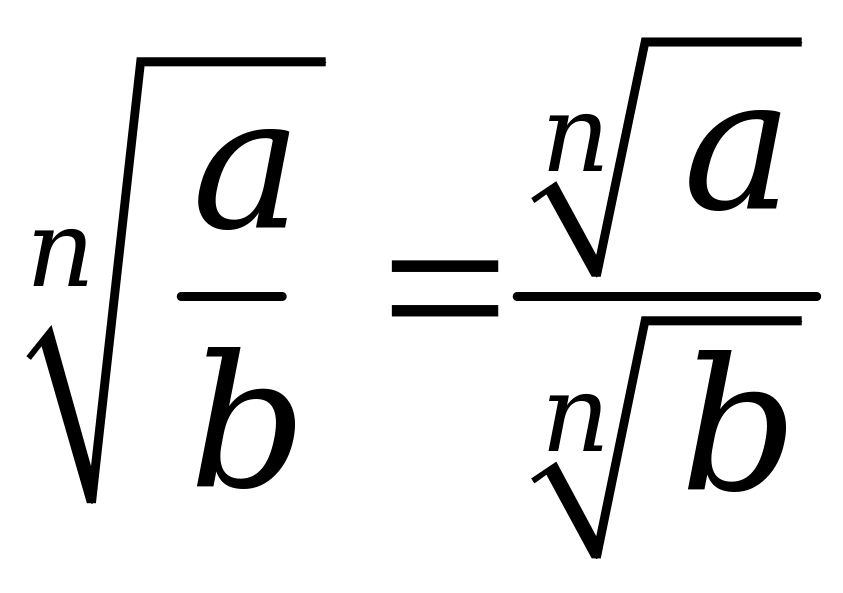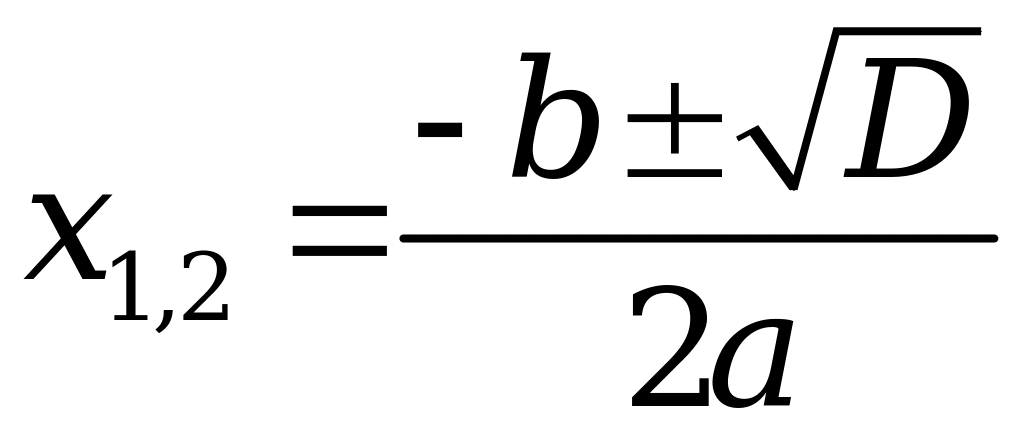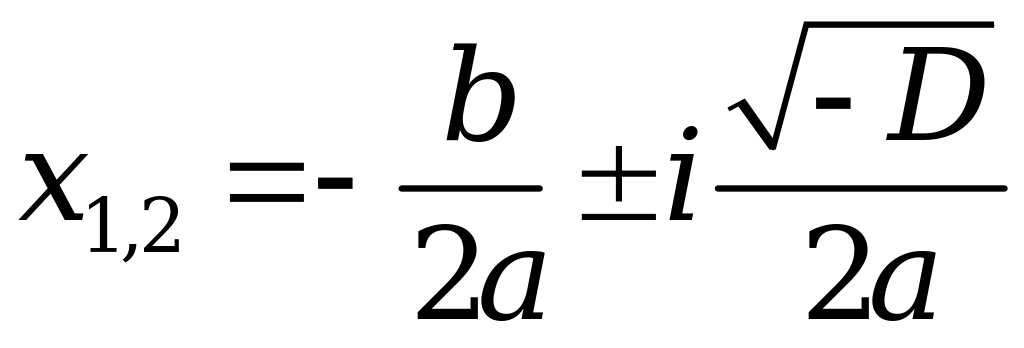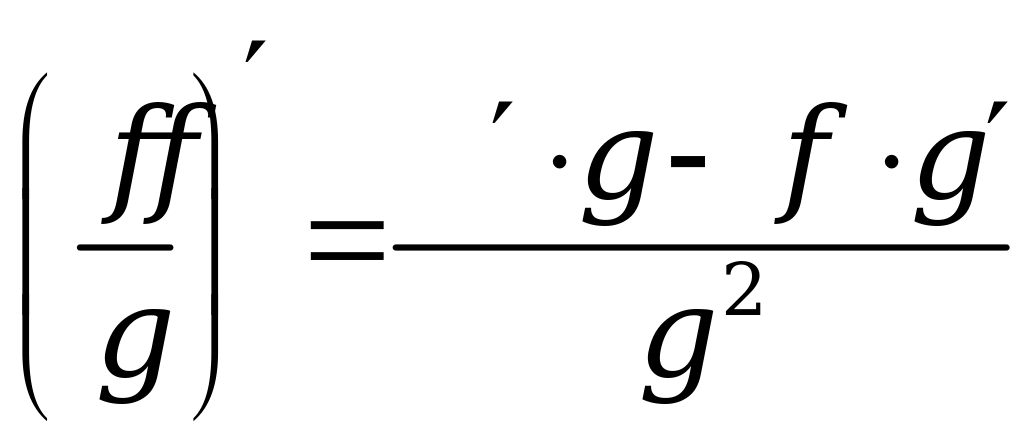43