m33751_4

.

Таким образом, общее решение линейного дифференциального уравнения первого порядка имеет вид

.

Частное решение получим из общего, используя для определения произвольной постоянной C заданное начальное условие: ,

.

После подстановки найденного значения постоянной C в общее решение линейного дифференциального уравнения, искомое частное решение приобретает вид

.

Линейные однородные дифференциальные уравнения второго порядка

Линейным однородным дифференциальным уравнением второго порядка называется уравнение вида

, (3.1)

где p и q – заданные действительные числа.

Заменим в этом дифференциальном уравнении производные неизвестной функции y соответствующими степенями неизвестного k ( заменим на , – на , а y – на ). В результате получим алгебраическое уравнение называемое характеристическим уравнением для данного дифференциального уравнения

. (3.2)

При решении дифференциального уравнения второго порядка с постоянными коэффициентами характеристическое уравнение представляет собой квадратный трехчлен, для корней которого, как известно, возможны три случая:

а) , – корни характеристического уравнения действительные, различные, если дискриминант уравнения положительный ;

б) – корни характеристического уравнения действительные, равные, если дискриминант уравнения равен нулю ;

в) действительные корни характеристического уравнения отсутствуют, если дискриминант уравнения отрицательный .

Общее решение линейного однородного дифференциального уравнения cтроится в полной зависимости от дискриминанта и корней характеристического уравнения (3.2)

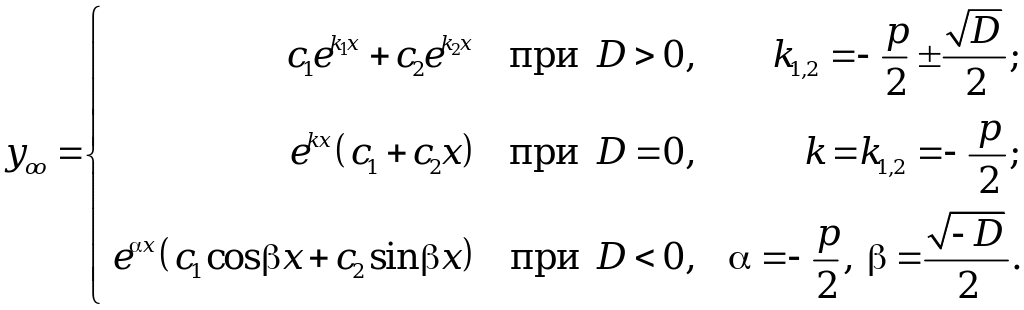(3.3)

Задание 5. Найти общие решения линейных однородных дифференциальных уравнений второго порядка.

Вариант 5.1	Вариант 5.2	Вариант 5.3
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.4	Вариант 5.5	Вариант 5.6
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.7	Вариант 5.8	Вариант 5.9
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.10	Вариант 5.11	Вариант 5.12
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.13	Вариант 5.14	Вариант 5.15
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.16	Вариант 5.17	Вариант 5.18
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.19	Вариант 5.20	Вариант 5.21
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.22	Вариант 5.23	Вариант 5.24
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.25	Вариант 5.26	Вариант 5.27
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Вариант 5.28	Вариант 5.29	Вариант 5.30
1. ;	1. ;	1. ;
2. ;	2. ;	2. ;
3. .	3. .	3. .

Решение типовых примеров

Пример 3.3. Найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами

.

Решение. Составим характеристическое уравнение

.

Дискриминант . Корни характеристического уравнения , – действительные и различные. Следовательно, строим общее решение по первой строке формулы (3.3)

.

Пример 3.4. Найти общее решение линейного однородного дифференциального уравнения

.

Решение. Составим характеристическое уравнение

.

Дискриминант . Корни характеристического уравнения действительные и равные . Следовательно, строим общее решение по второй строке формулы (3.3)

.

Пример 3.5. Найти общее решение линейного однородного дифференциального уравнения

.

Решение. Составим характеристическое уравнение

.

Дискриминант . Следовательно, строим общее решение по третьей строке формулы (3.3) для ,

.

Линейные неоднородные дифференциальные уравнения второго порядка

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид

. (3.4)

Оно отличается от однородного наличием в правой части некоторой функции .

Общее решение неоднородного линейного дифференциального уравнения (3.4) представляет собой сумму общего решения соответствующего однородного уравнения (3.1) и какого-либо частного решения неоднородного уравнения (3.4)

. (3.5)

Таким образом, чтобы найти общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами и правой частью специального вида необходимо следующее:

а) найти общее решение однородного дифференциального уравнения (3.1) (см. выше);

б) указать вид частного решения неоднородного дифференциального уравнения (3.4) (см. ниже);

в) найти числовые значения неопределенных коэффициентов частного решения (см. ниже);

г) выписать общее решение неоднородного дифференциального уравнения (3.4) в виде суммы (3.5).

Вид частного решения неоднородного дифференциального уравнения (3.4) зависит от вида функции . Рассмотрим один из наиболее простых случаев с правой частью вида

, (3.6)

где , , …, – заданные постоянные коэффициенты.

Для нахождения частного решения в этом случае необходимо:

30