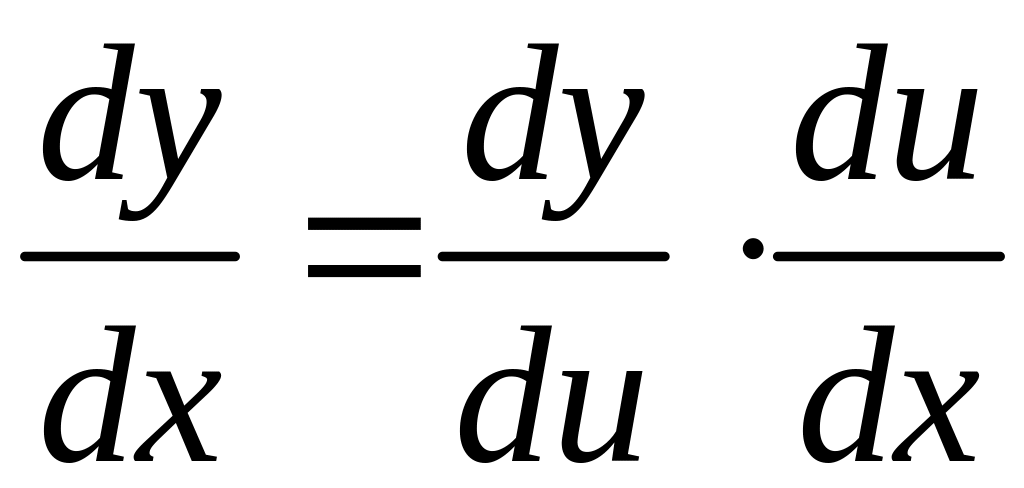Вариант 14.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 15.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 16.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3. |
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 17.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 18.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 19.
I. |
1.
|
2.
|
3.
|
4.
|
5. |
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 20.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 21.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7. |
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 22.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 23.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1. |
2. |
||
Вариант 24.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 25.
I. |
1.
|
2. |
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 26.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7. |
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 27.
I. |
1.
|
2.
|
3. |
4.
|
5.
|
6. |
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 28.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7. |
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Решение типовых заданий
ПРИМЕР 1. Исследовать на сходимость следующие числовые ряды:
1)
;
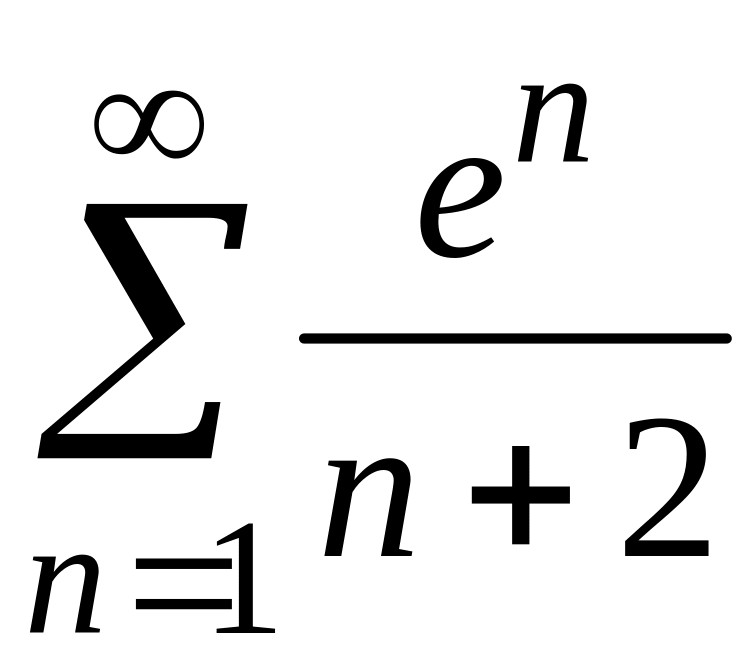2)
;
3)
;
4)
.
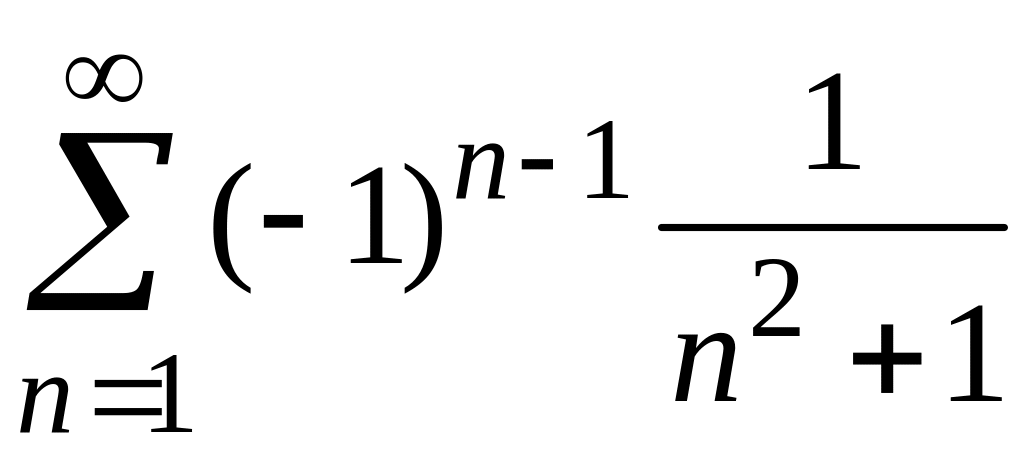Решение.
1) Для данного знакоположительного ряда не выполняется необходимый признак сходимости. Действительно,
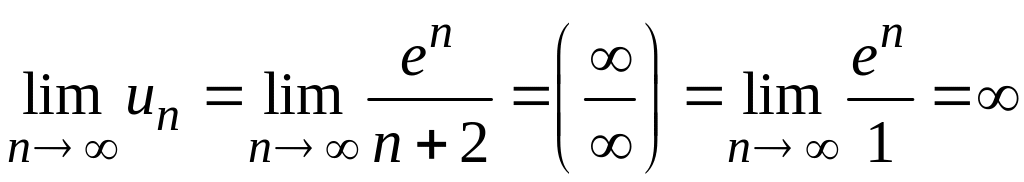
(при
вычислении предела воспользовались
правилом Лопиталя), то есть
.
Следовательно, ряд расходится.
2) В этом случае воспользуемся признаком сравнения:
.
Ряд
(гармонический), как известно, расходится,
поэтому расходится и заданный ряд.
3) При исследовании на сходимость данного знакоположительного ряда воспользуемся признаком Даламбера.
Общий
член этого ряда
.
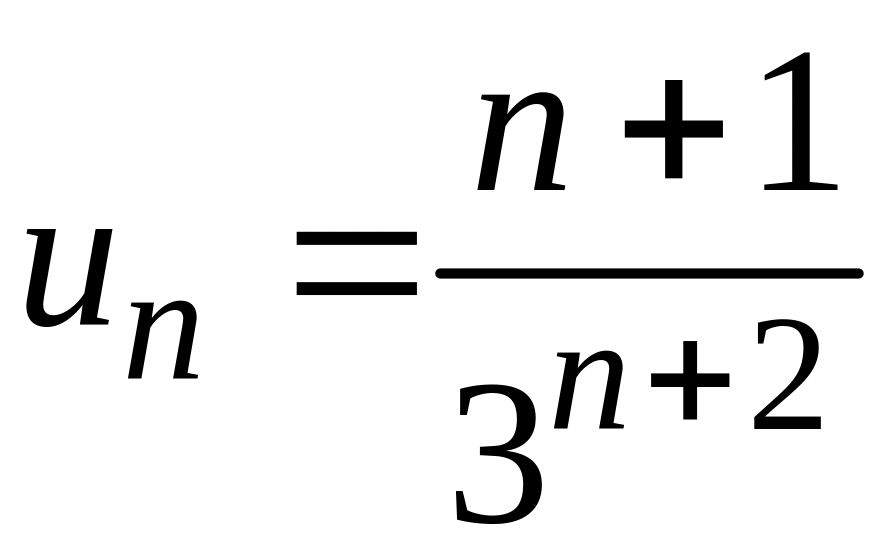Тогда
.
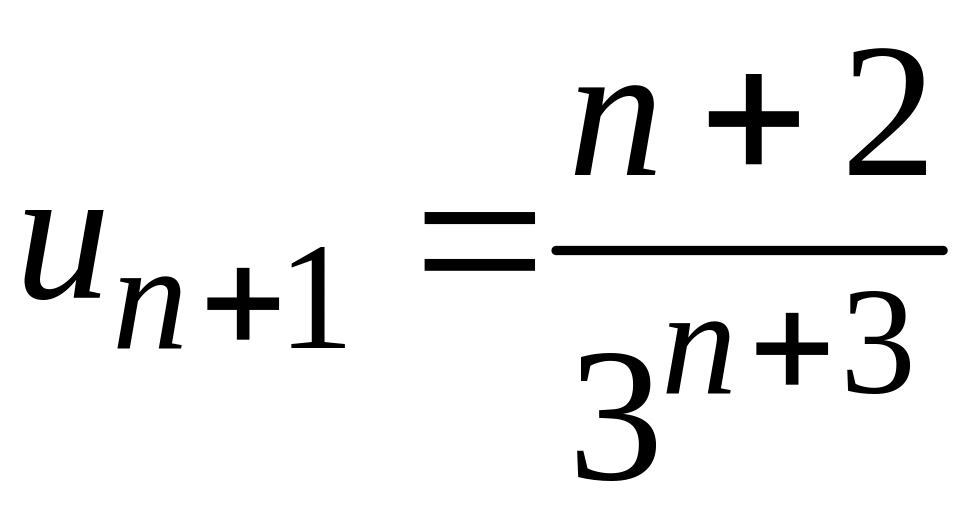В соответствии с признаком Даламбера вычисляем предел
.
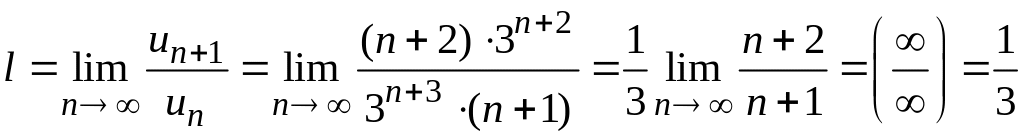Так
как
,
делаем вывод о сходимости исходного
ряда.
4) Заданный ряд знакочередующийся:
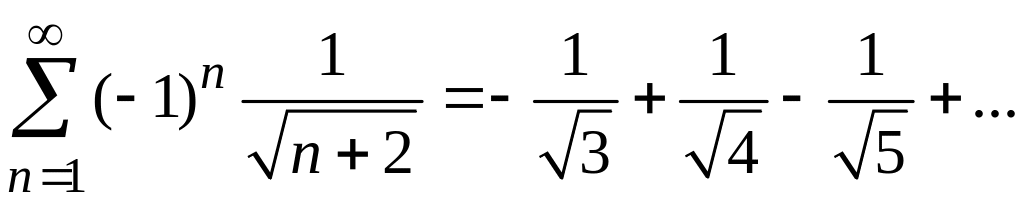
Рассмотрим
абсолютные величины членов исходного
ряда:
.
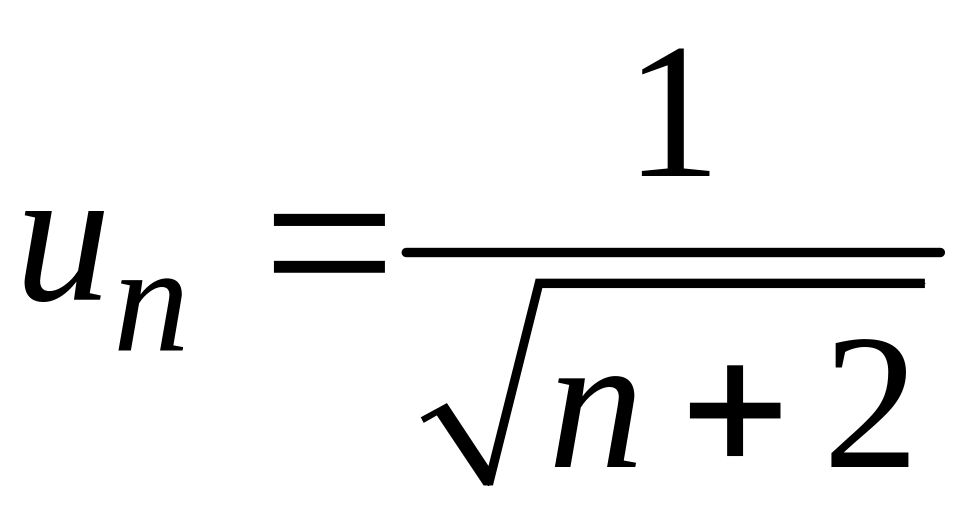При этом
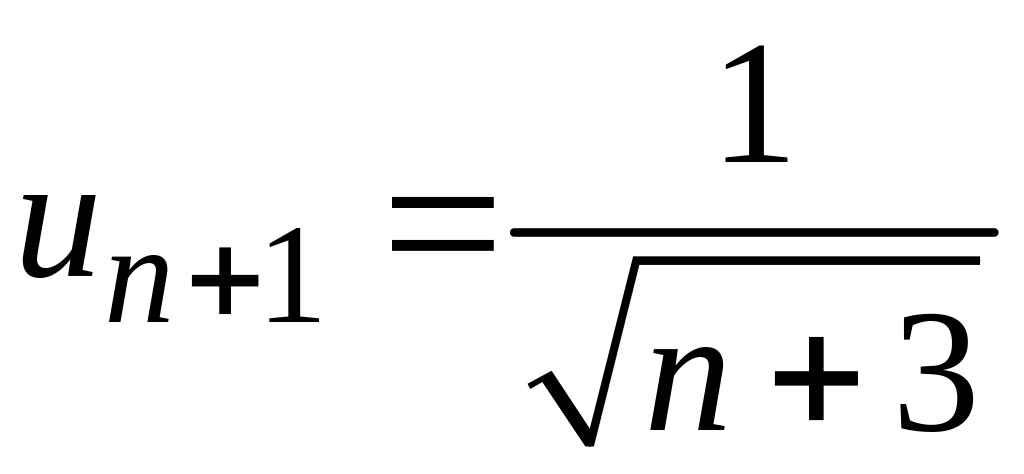и, очевидно,
,
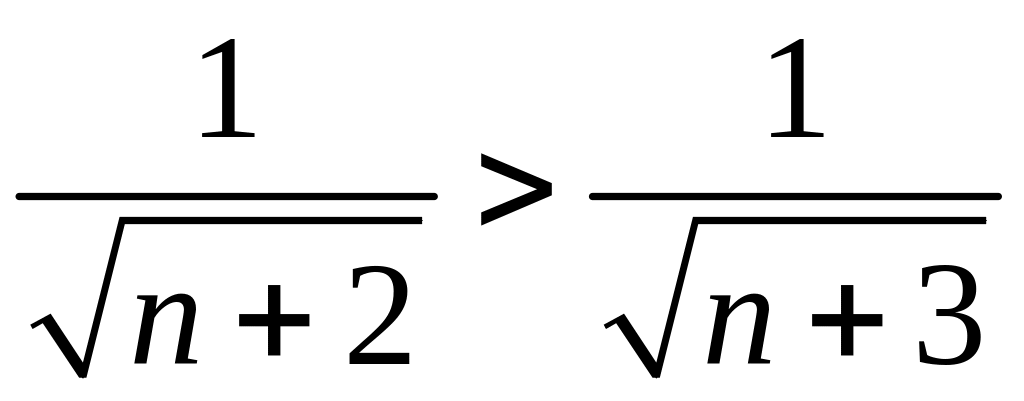то есть
для любого
Таким образом, члены заданного ряда
убывают по абсолютной величине. Кроме
того,
,
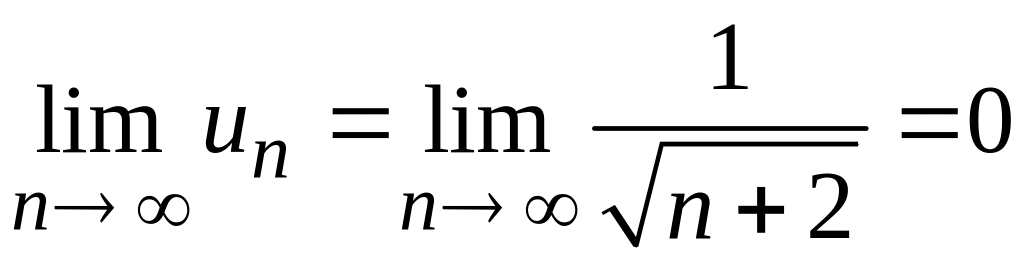поэтому выполнены условия признака Лейбница, т. е. ряд сходится.
ПРИМЕР
2.
Найти
радиус и интервал сходимости степенного
ряда
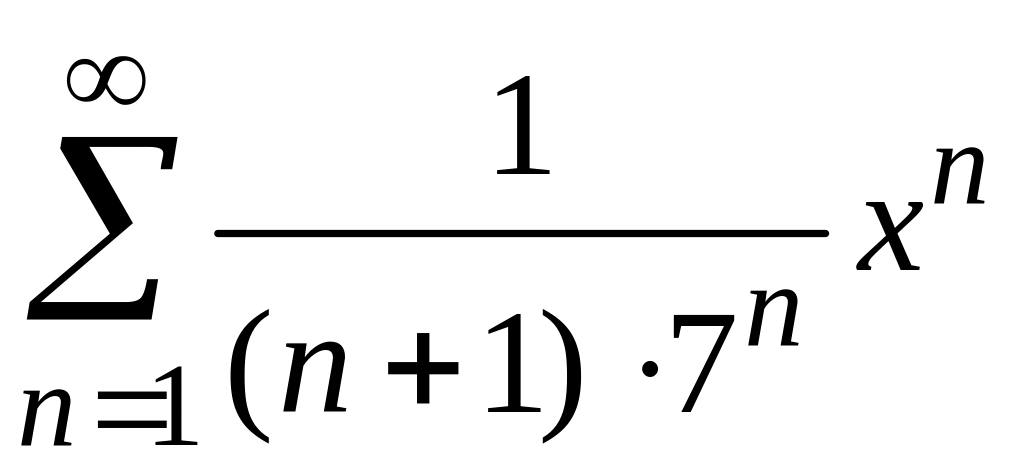и
определить поведение ряда на концах
интервала сходимости.
Решение.
Имеем
коэффициенты при членах ряда, занимающих
места n
и n
+ 1.
Ищем радиус сходимости ряда:
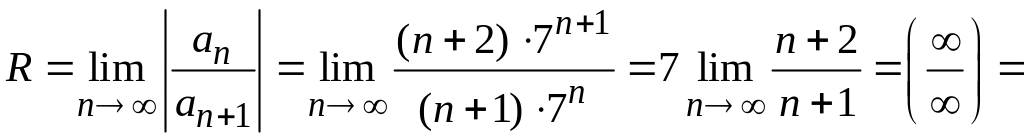7.
Интервал
сходимости ряда имеет вид
,
то есть в нашем примере это (7,
7).
ПРИМЕР 3. Вычислить с точностью до 0,001 интеграл
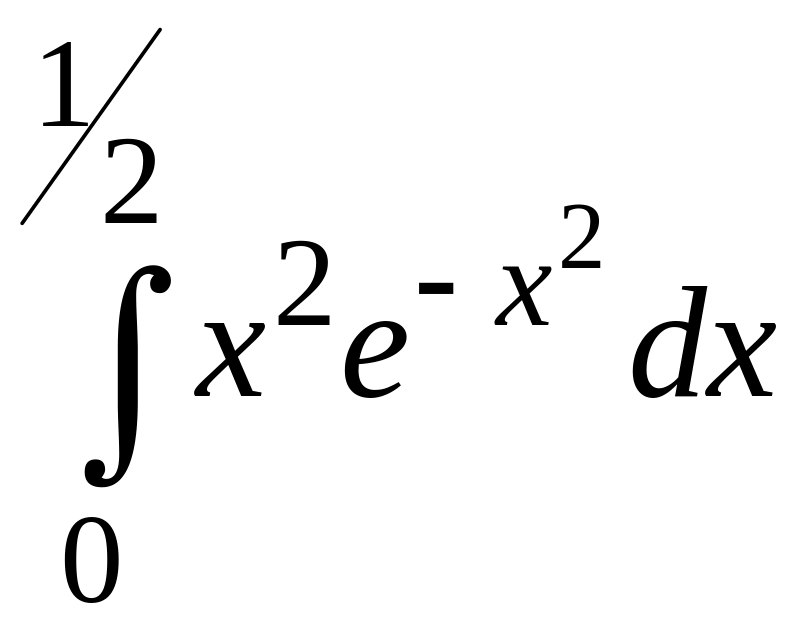
путем предварительного разложения подынтегральной функции в степенной ряд и почленного интегрирования этого ряда.
Решение.
Запишем
разложение функции
в степенной ряд
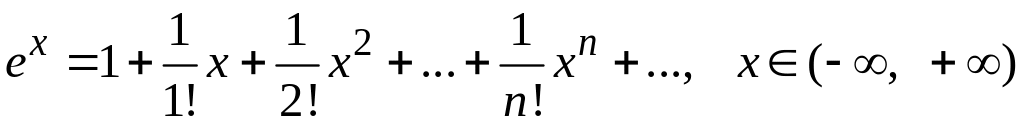
и
заменим x
на
.
Тогда получим
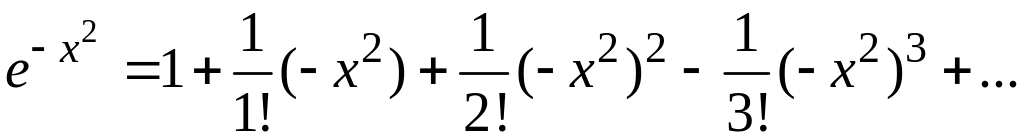
Умножая
этот ряд почленно на
,
будем иметь
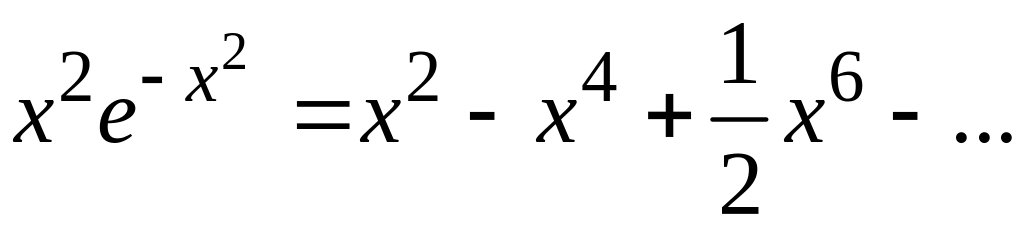
Следовательно,
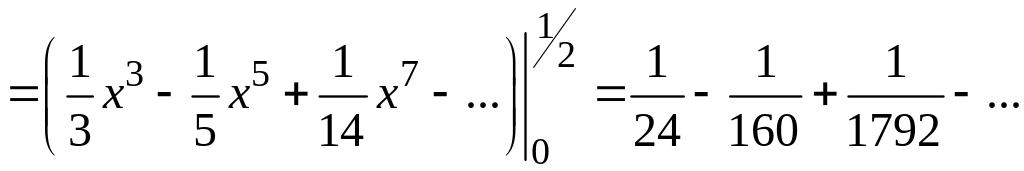
Полученный числовой знакочередующийся ряд удовлетворяет условиям признака Лейбница. Третий член этого ряда по абсолютной величине меньше 0,001, поэтому для обеспечения требуемой точности нужно просуммировать первые два члена ряда и результат округлить до 0,001. Итак,
ПРИМЕР 4. Найти три первые отличные от нуля члена разложения в степенной ряд решения задачи Коши
.
Решение.
Будем считать,
что решение задачи Коши
может
быть представлено рядом Маклорена
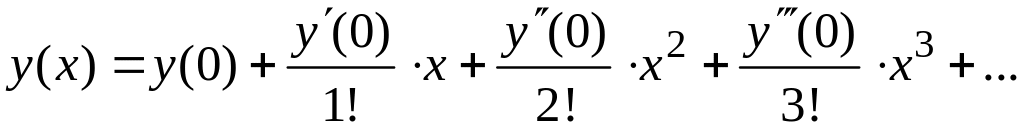
Вычисляем последовательно:
1;
1;
3.
Задача решена. Результат решения имеет вид
.
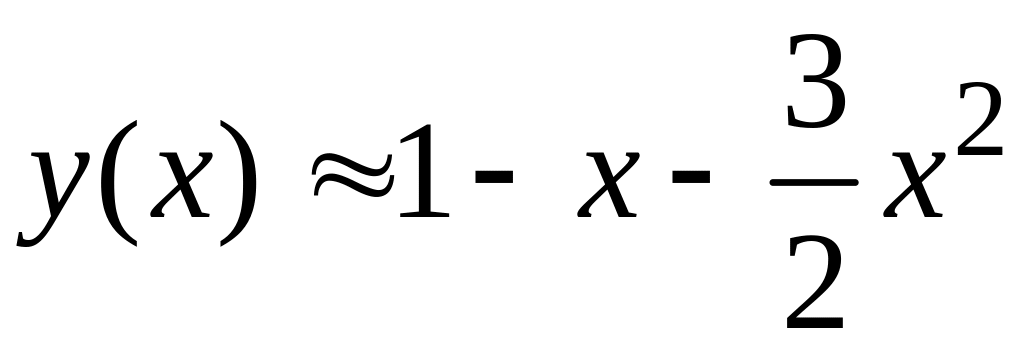Приложения Приложение 1
Таблица производных основных элементарных функций
и правил дифференцирования
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
|
|
|
5. |
|
|
|
|
|
6. |
а)
|
б)
|
|
в)
|
|
|
г)
д)
если задана сложная функция
|
|
.
.
;
;
;
;
;
;
;
;
;
,
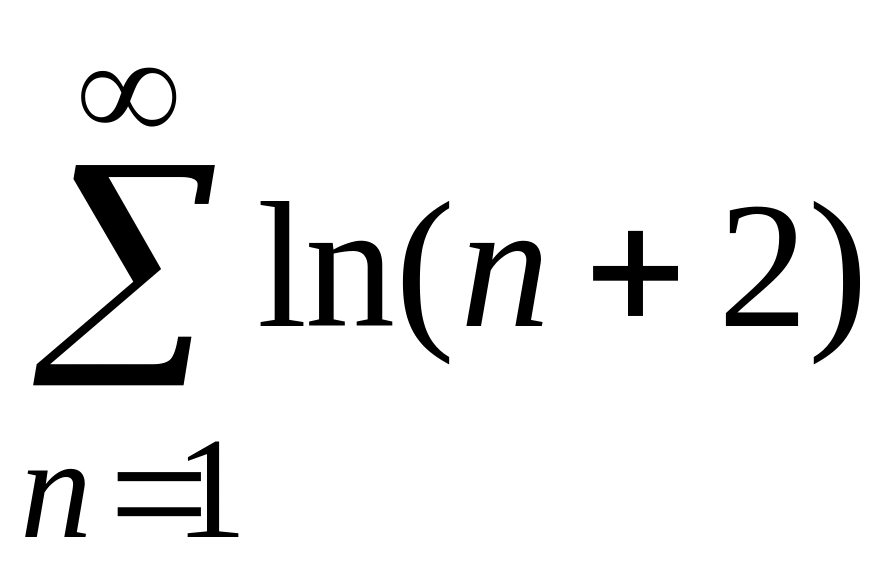
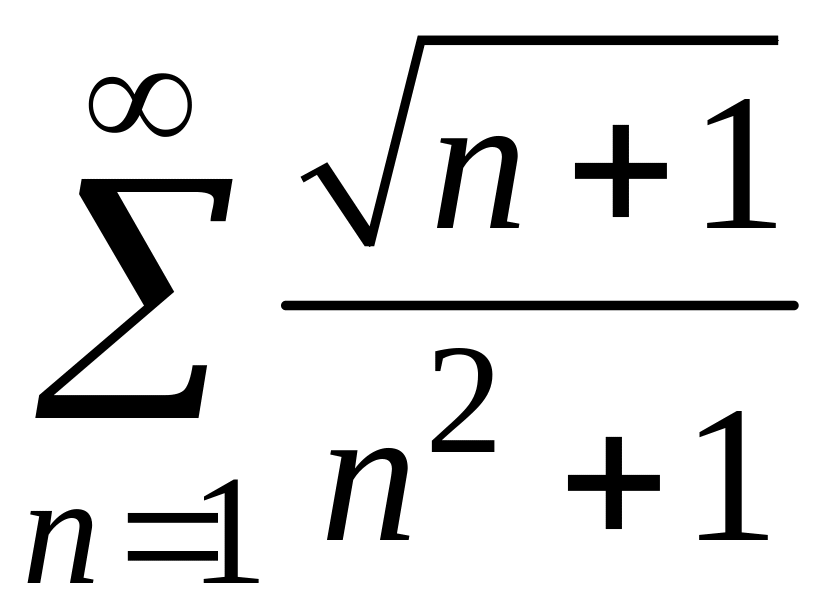
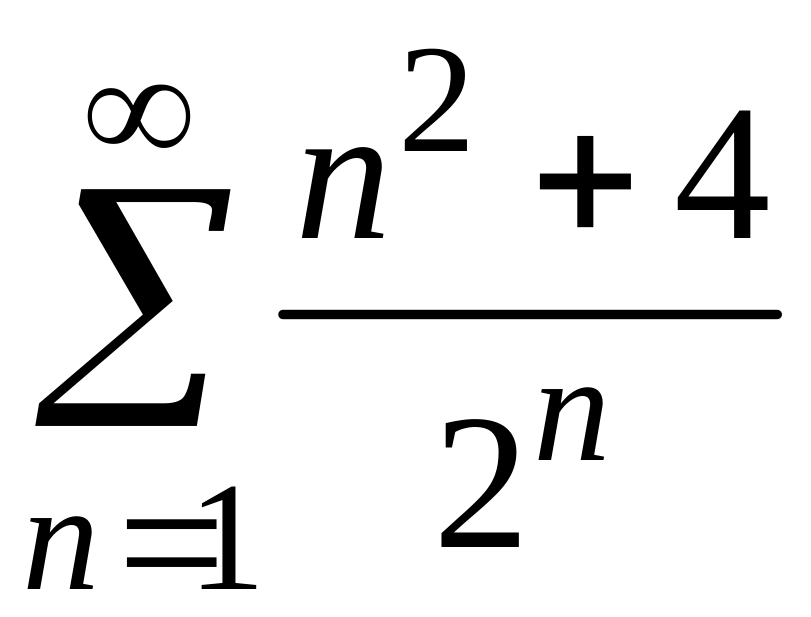
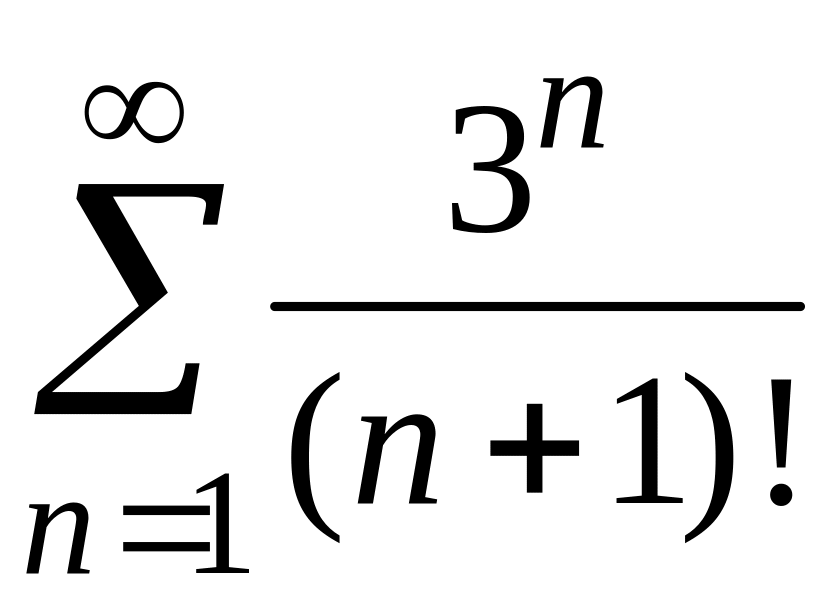
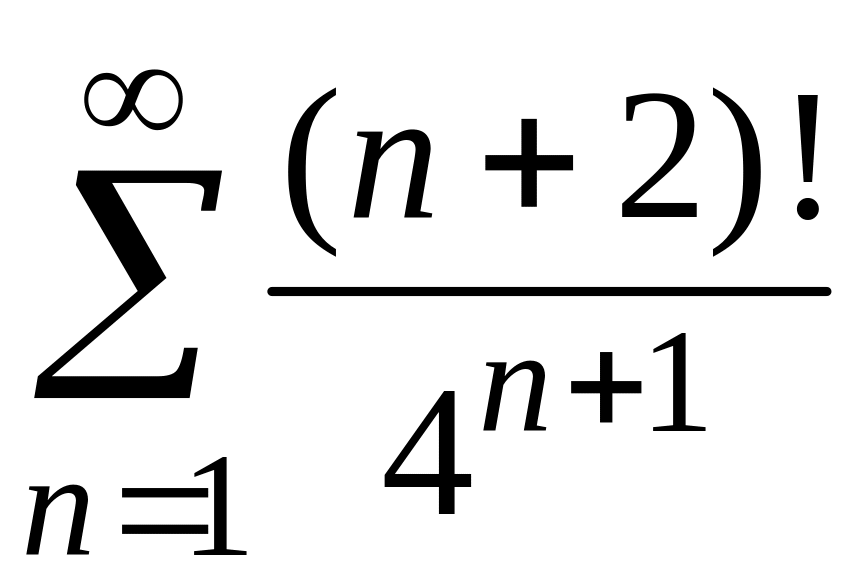
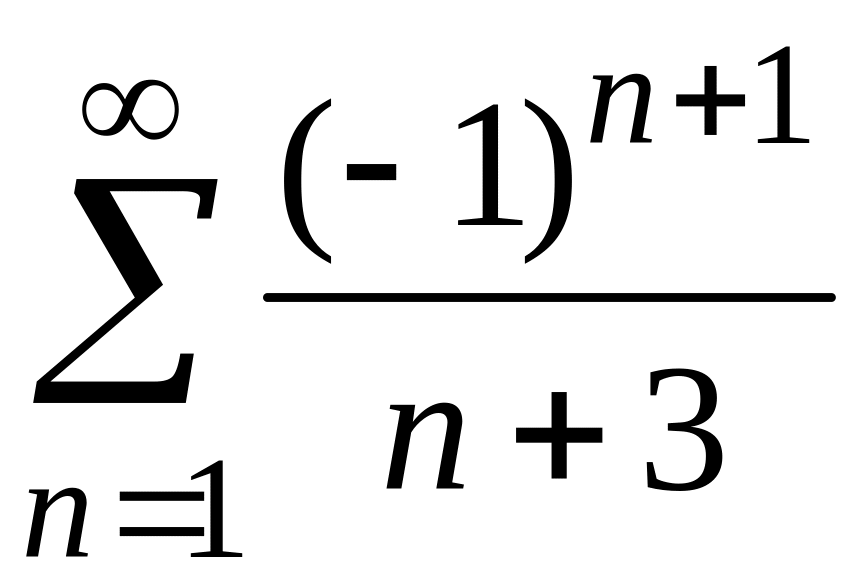
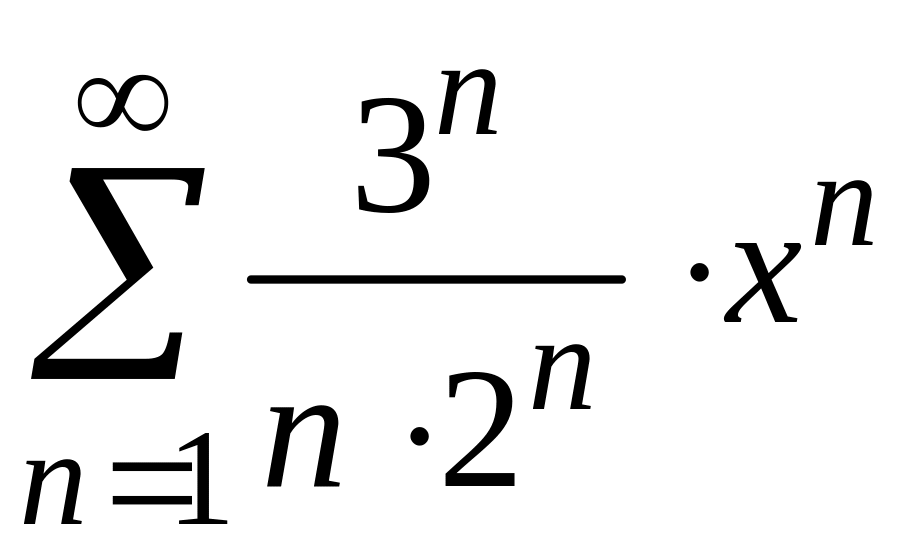
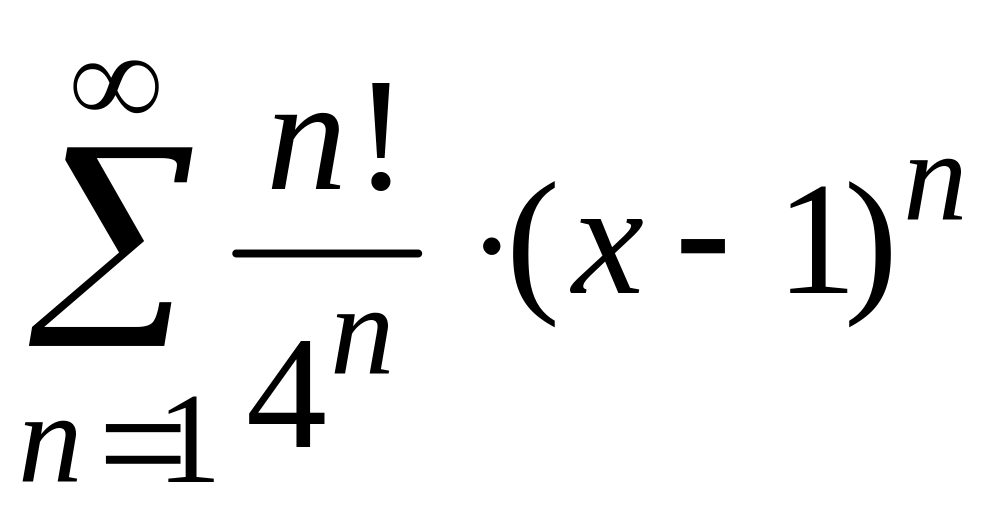
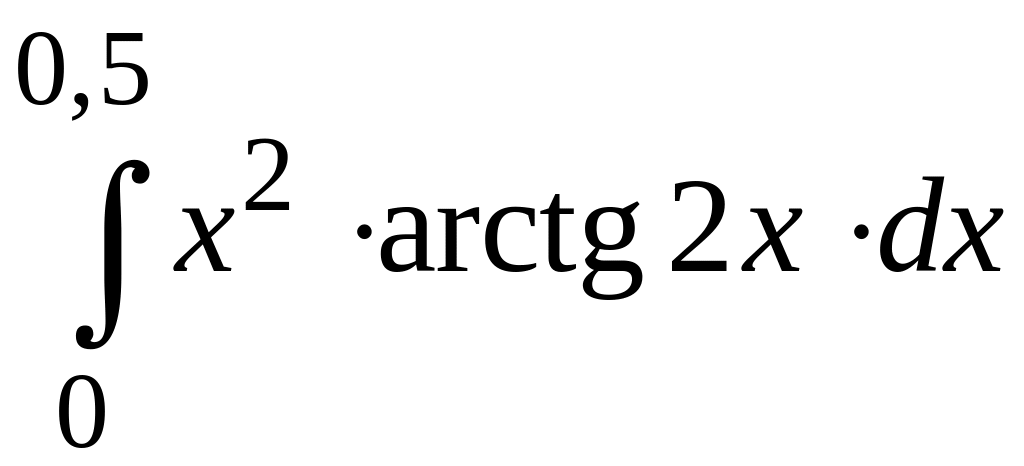
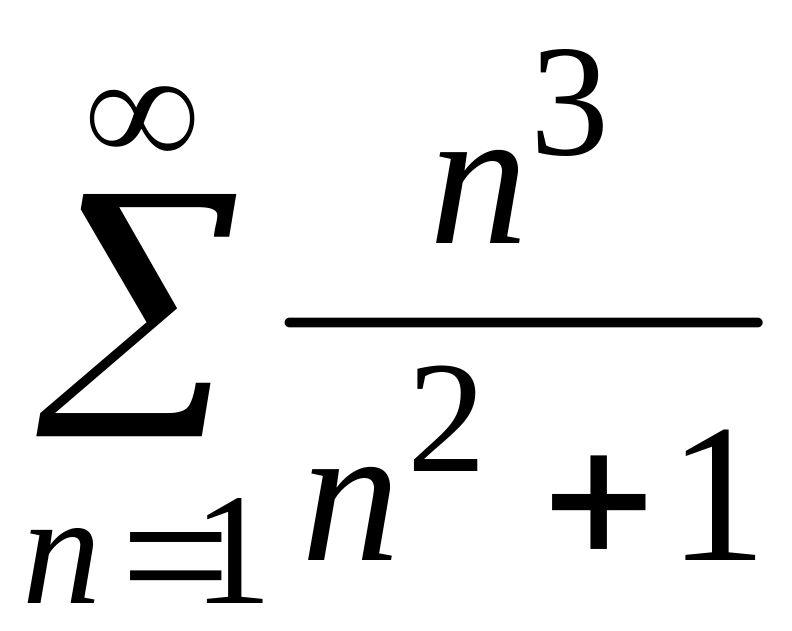
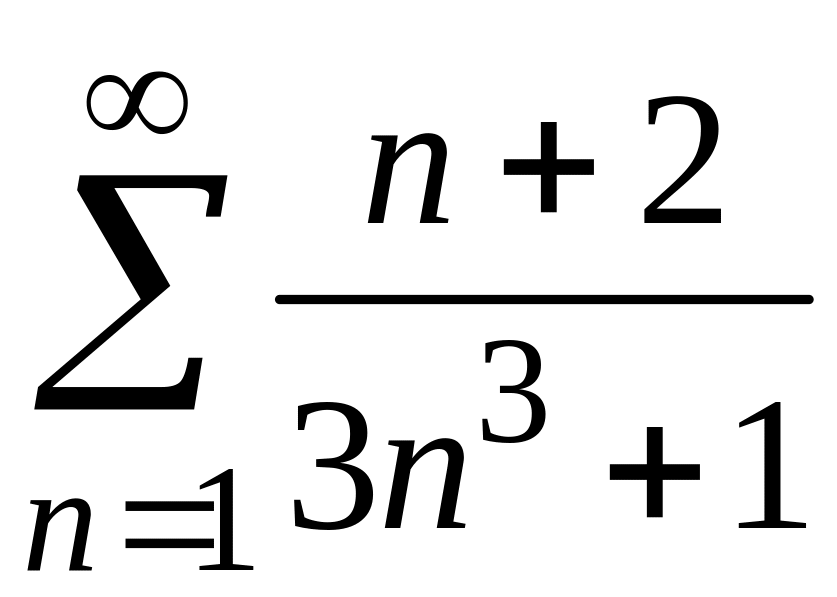
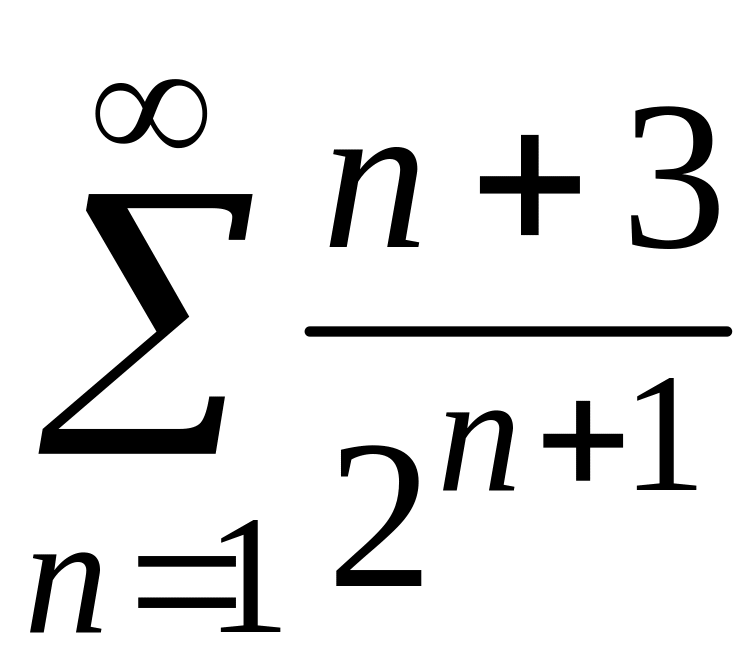
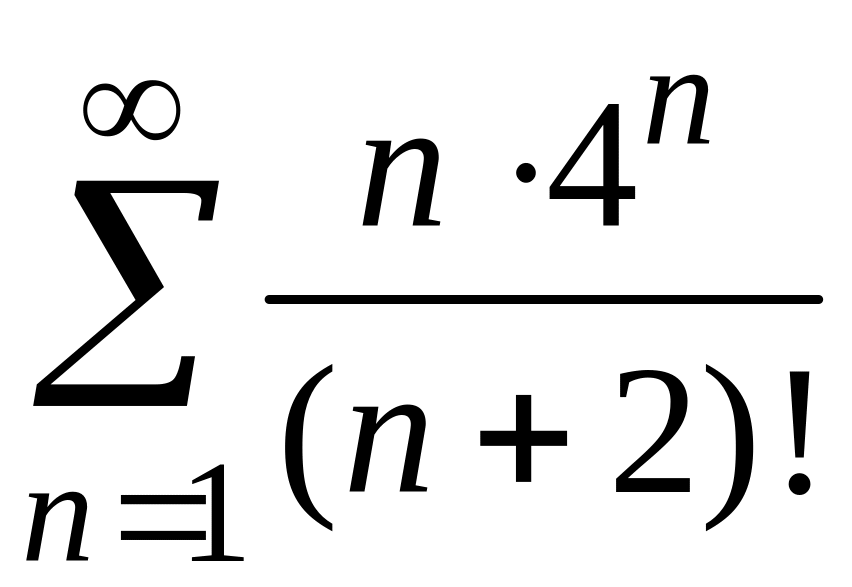
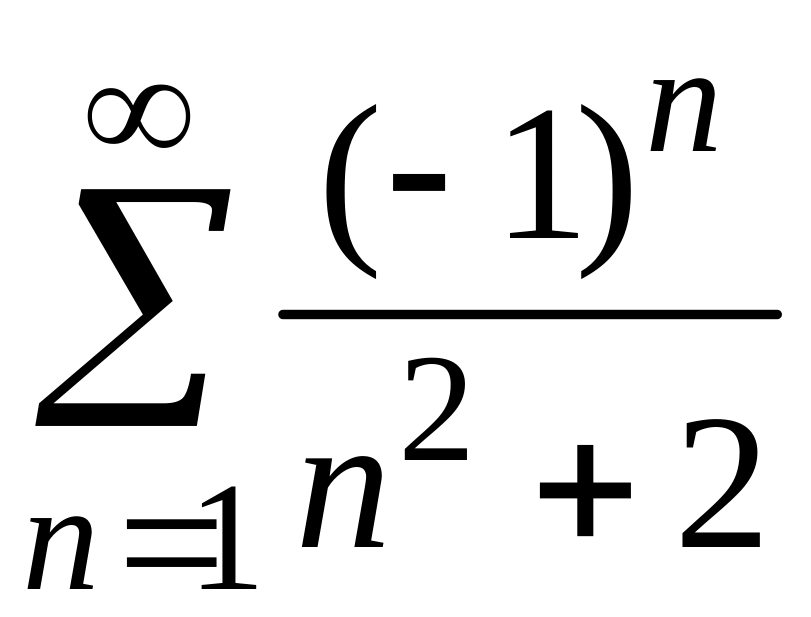
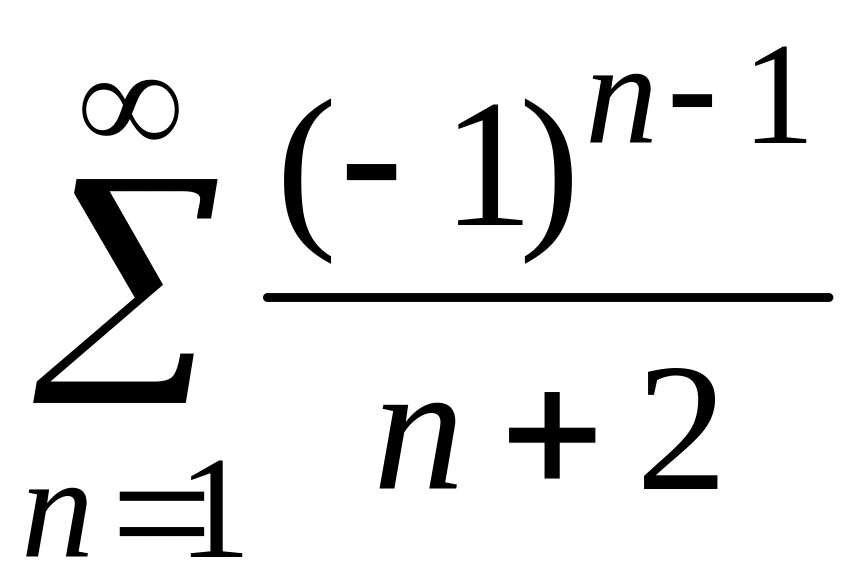
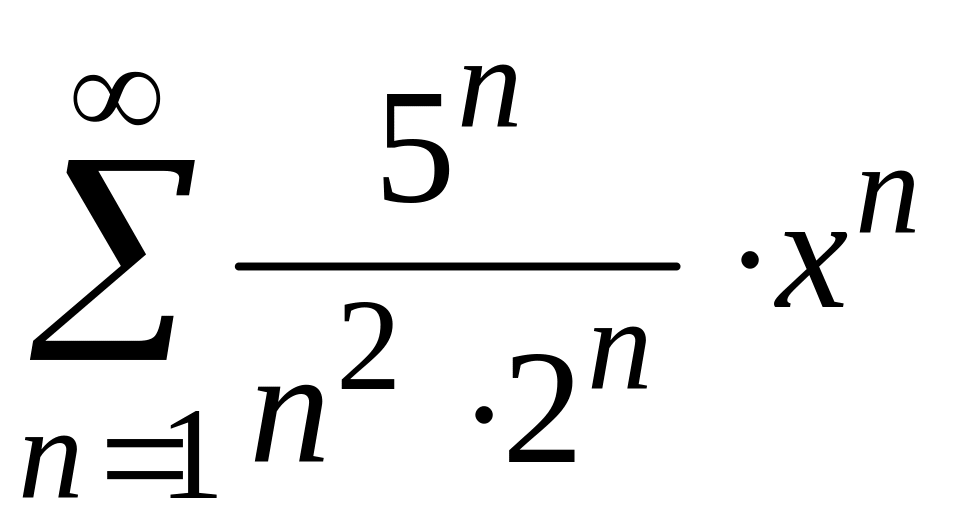
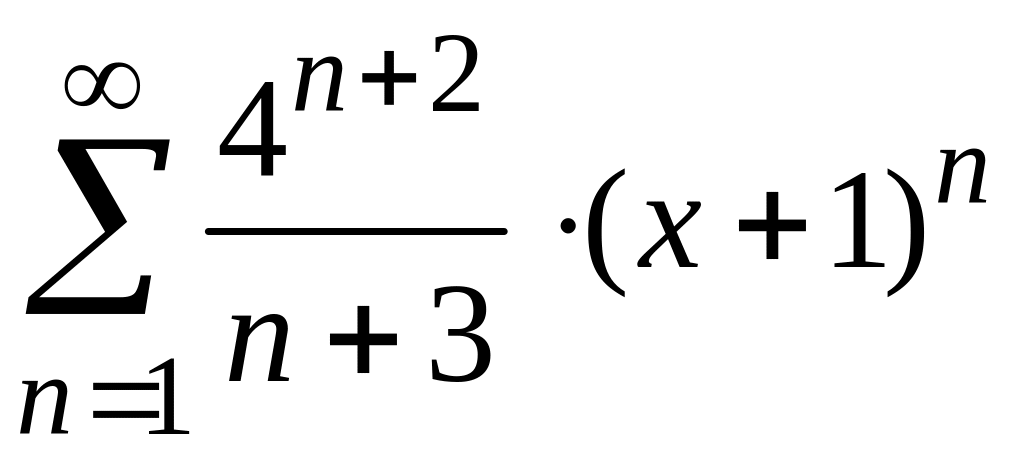
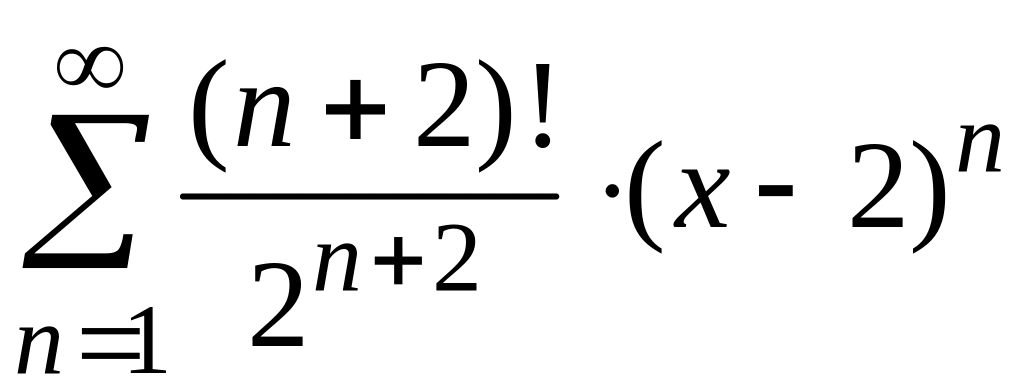
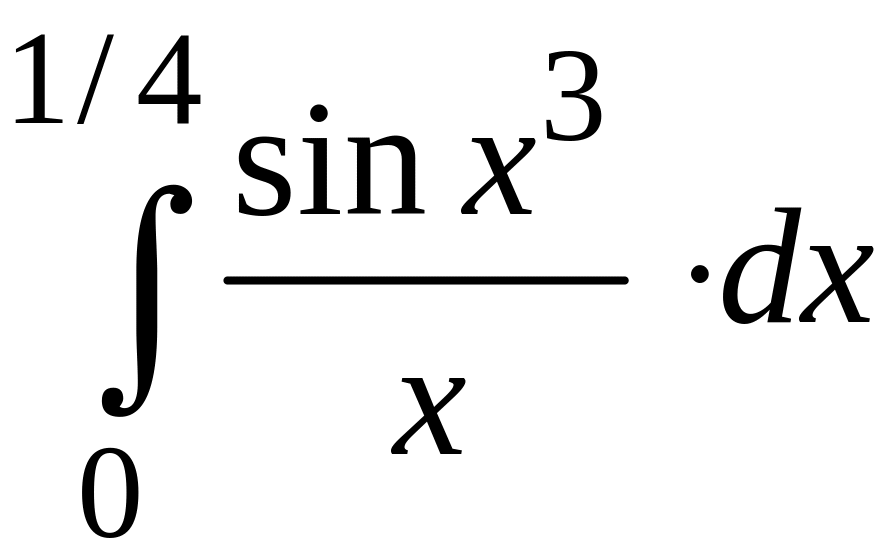
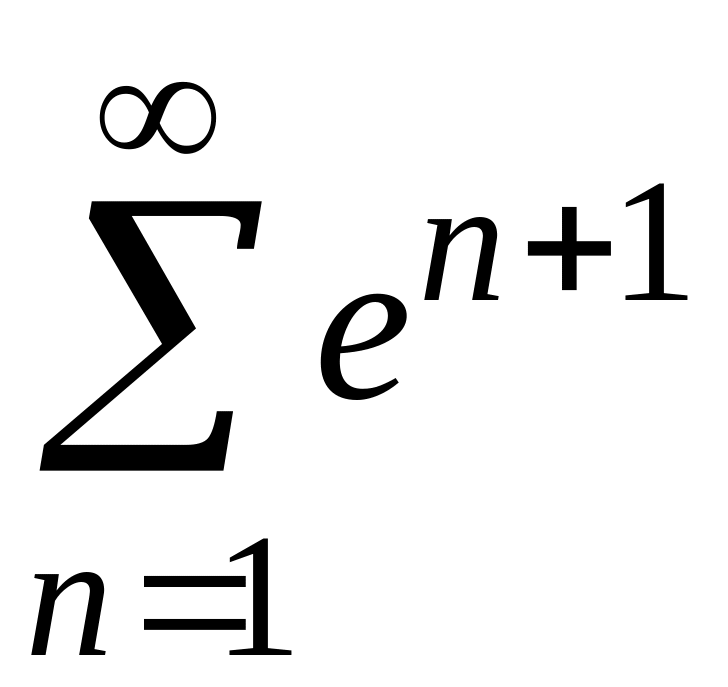
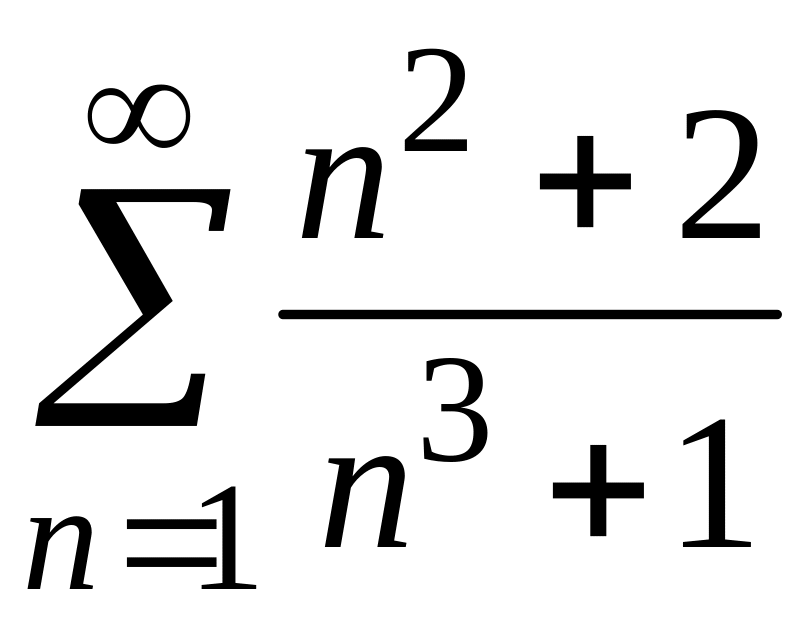
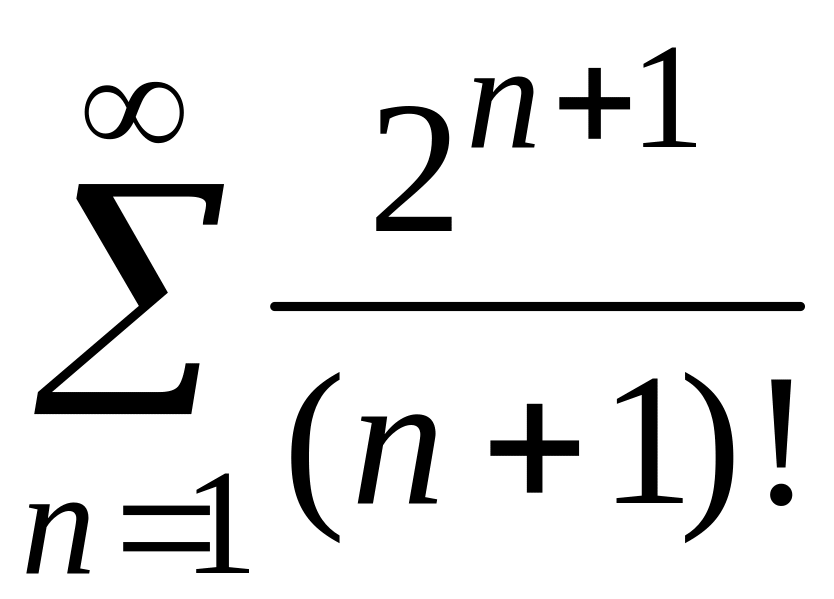
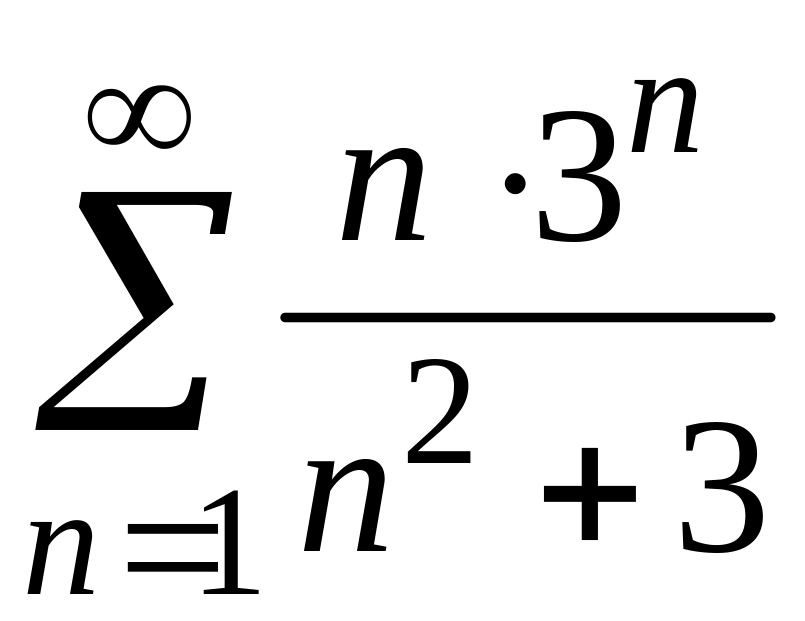
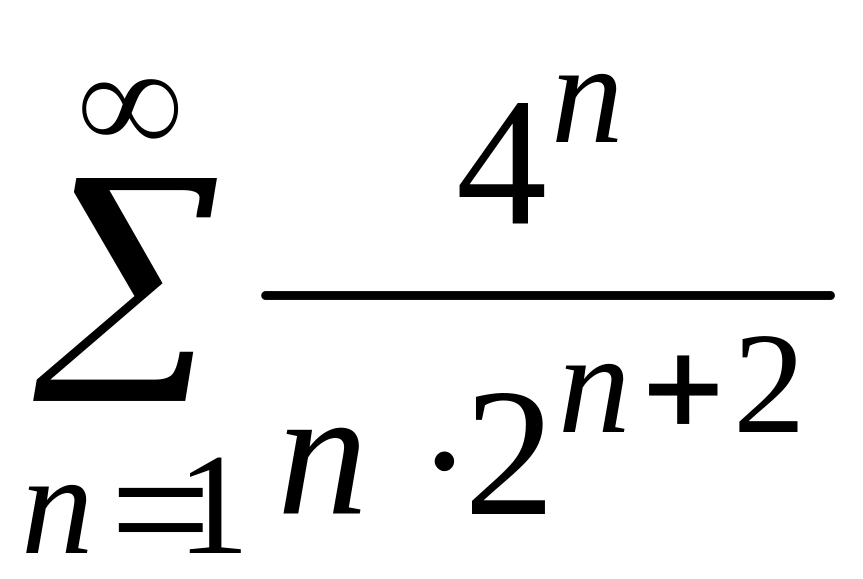
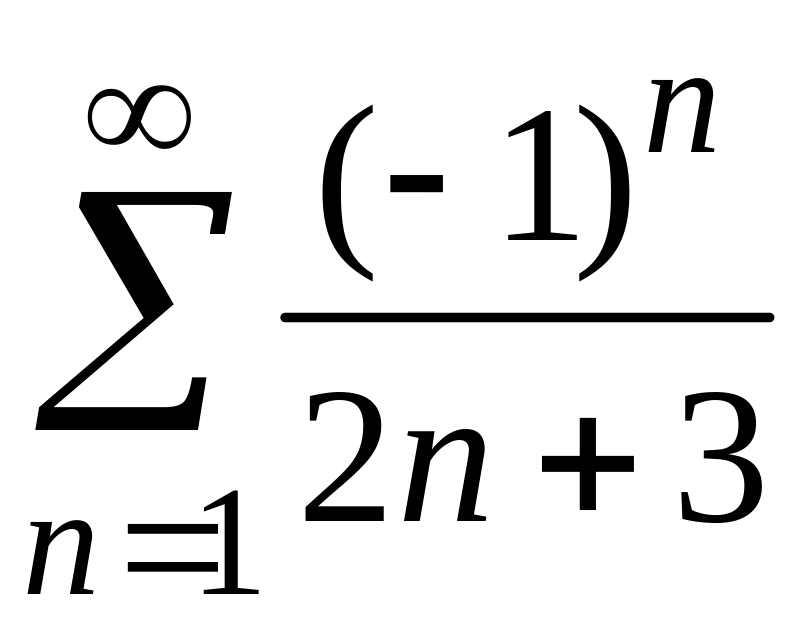
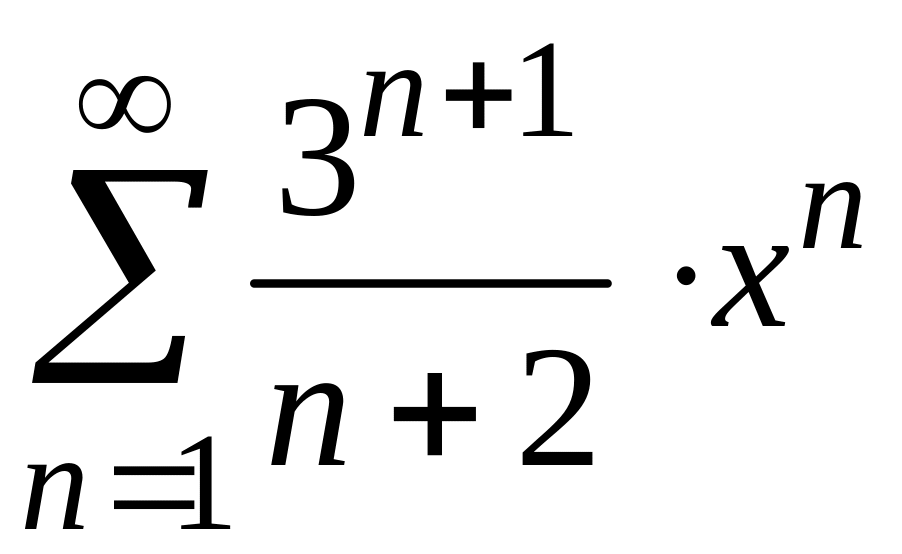
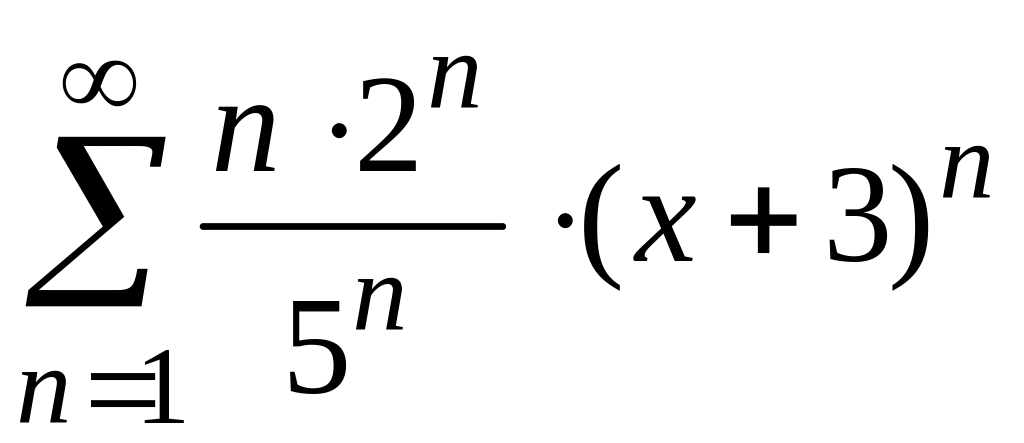
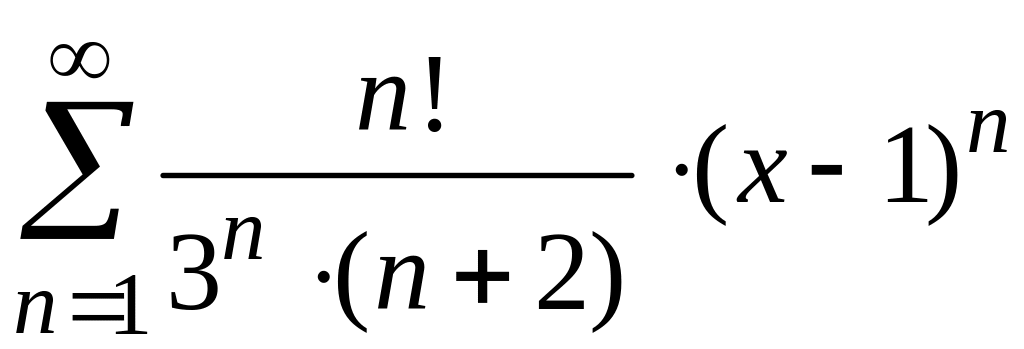
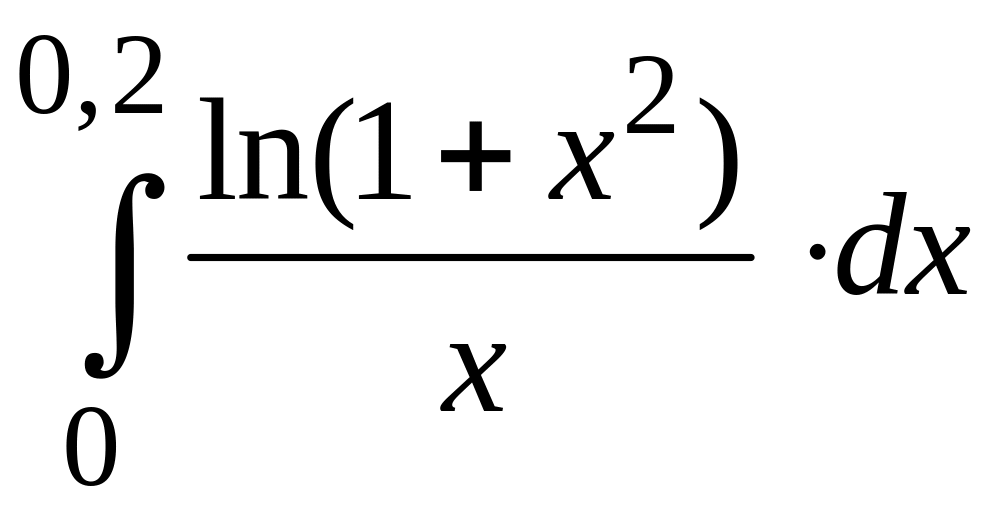
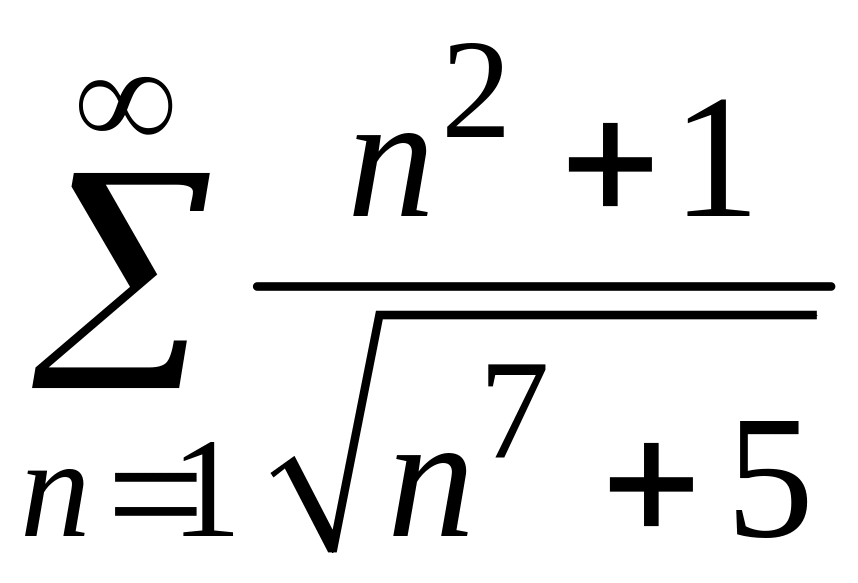
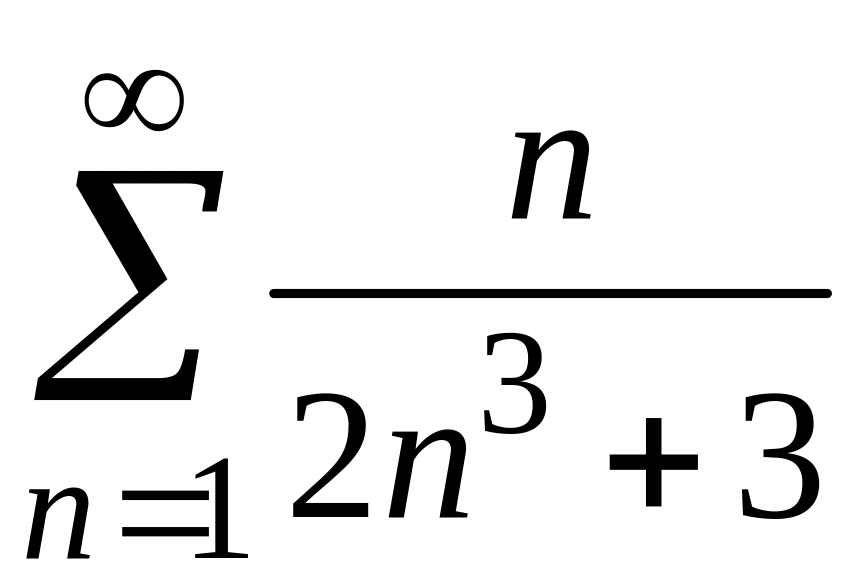
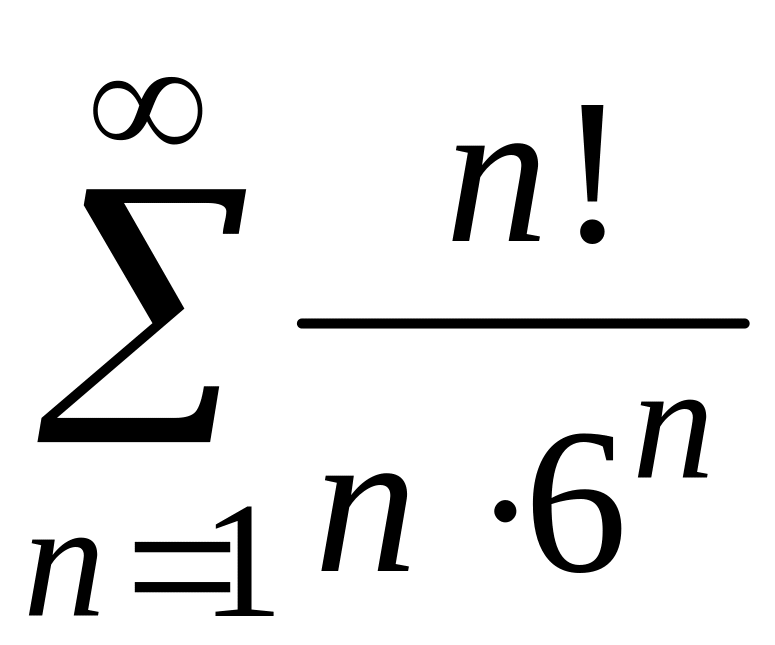
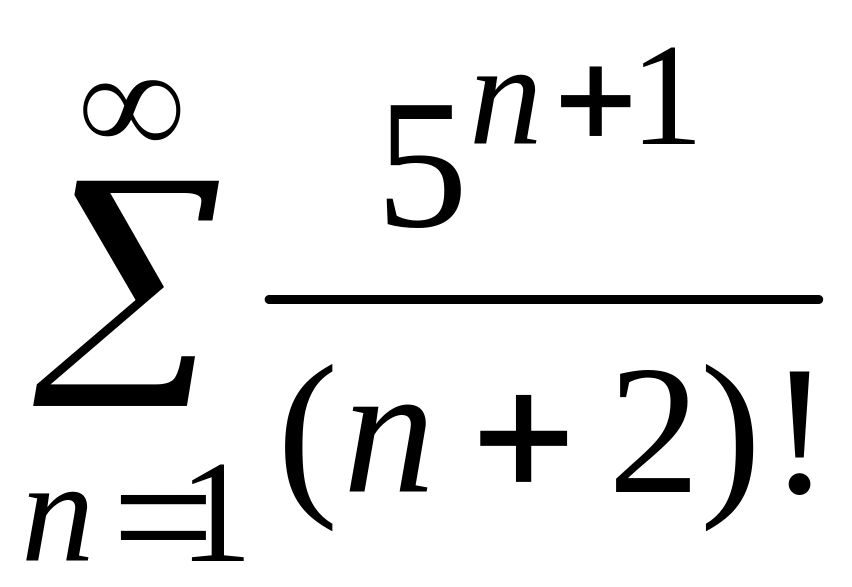
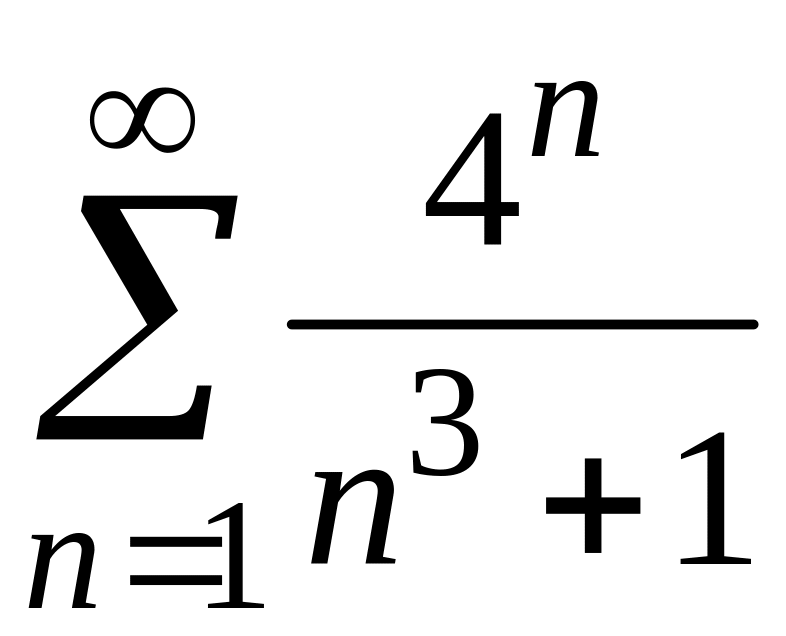
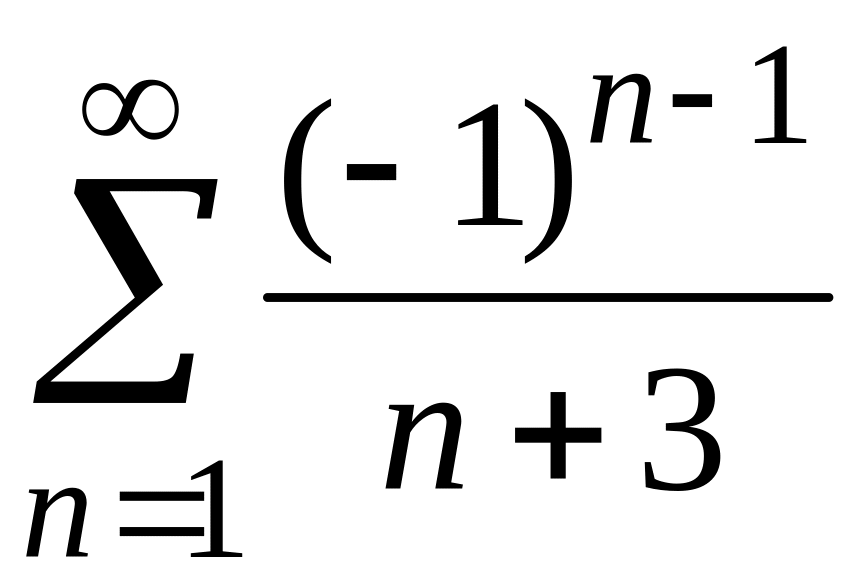
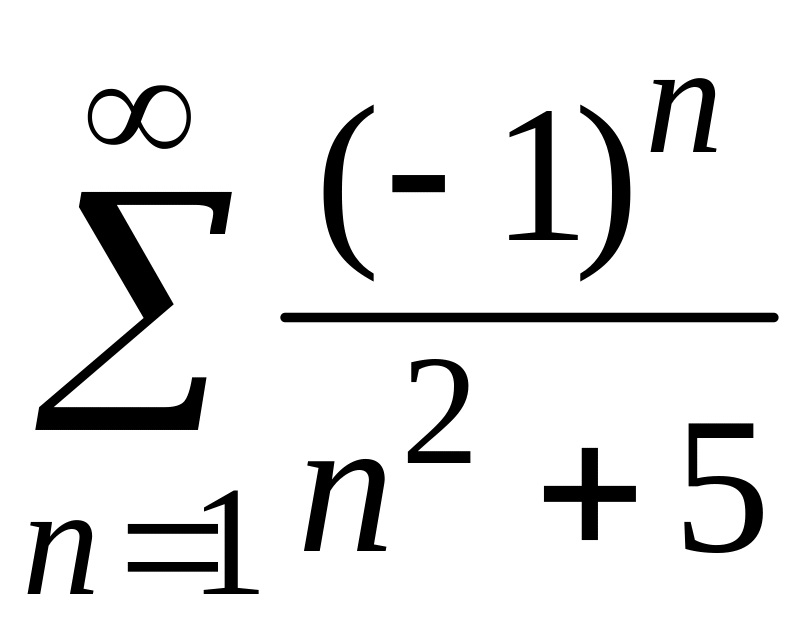
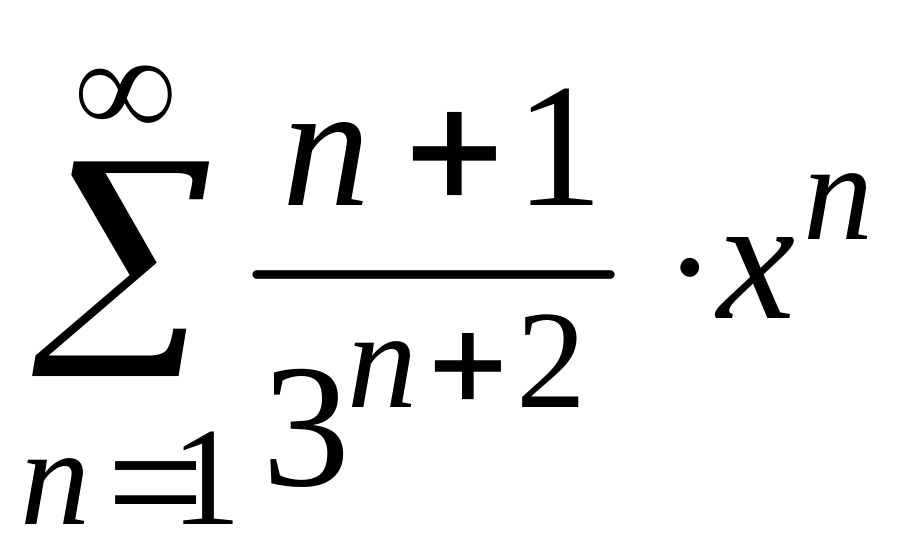
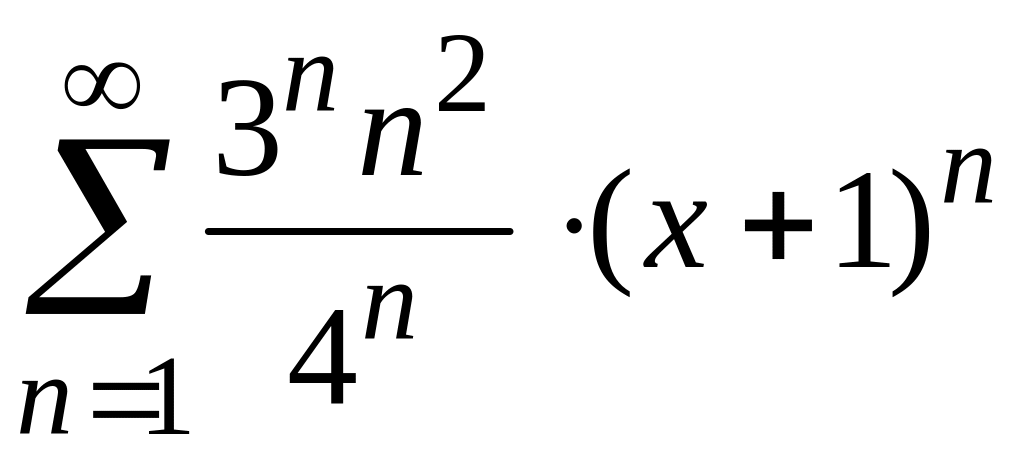
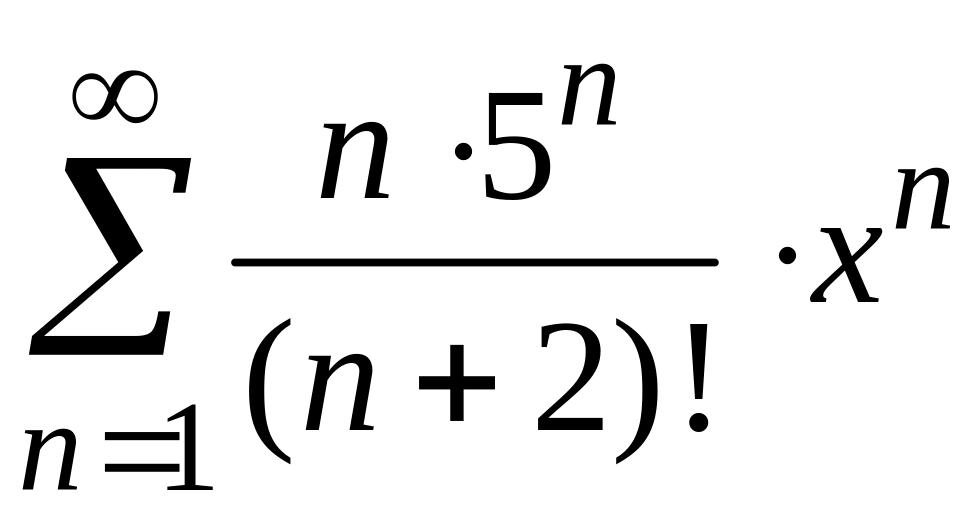
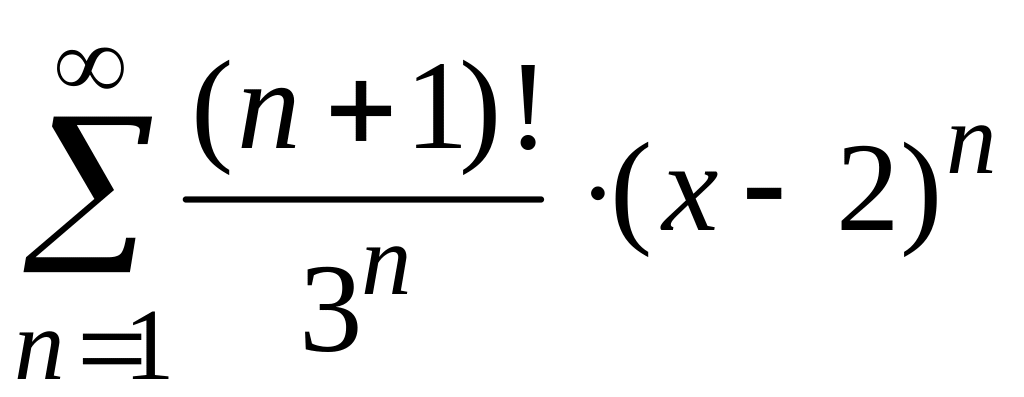
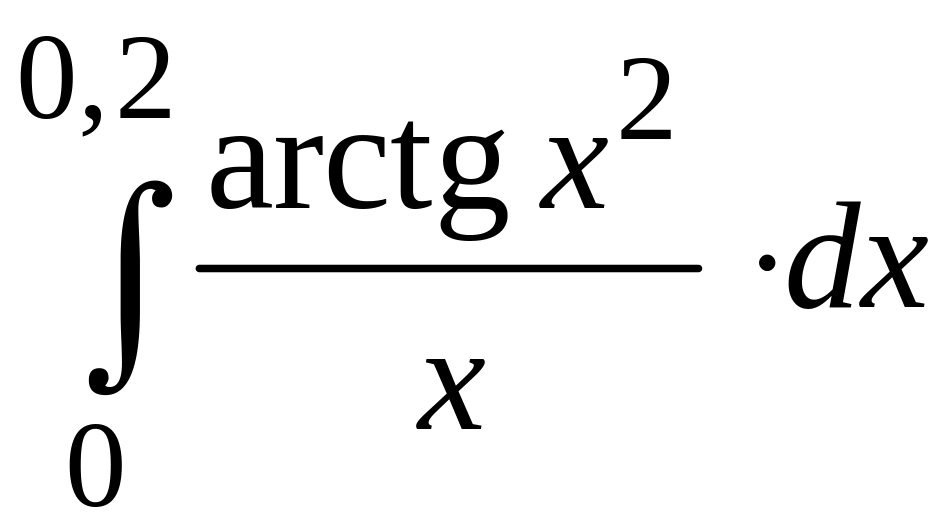
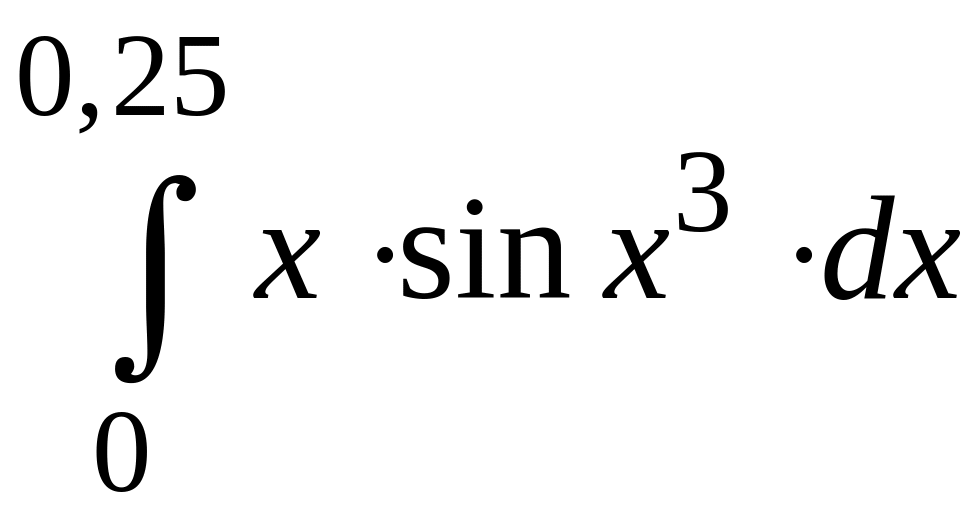
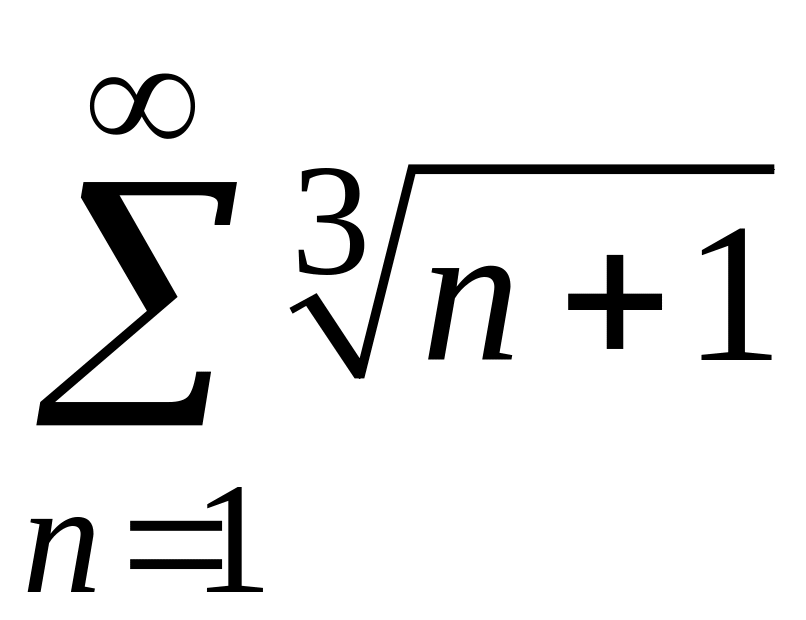
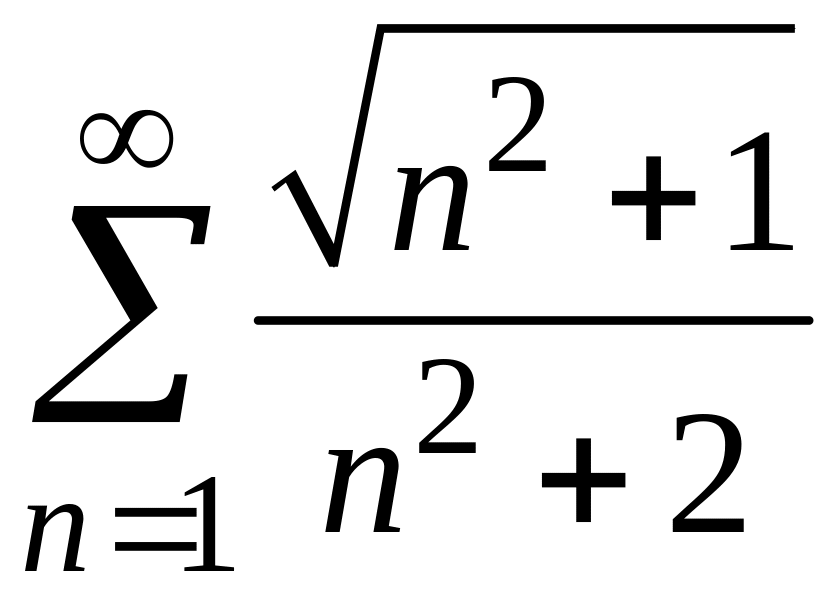
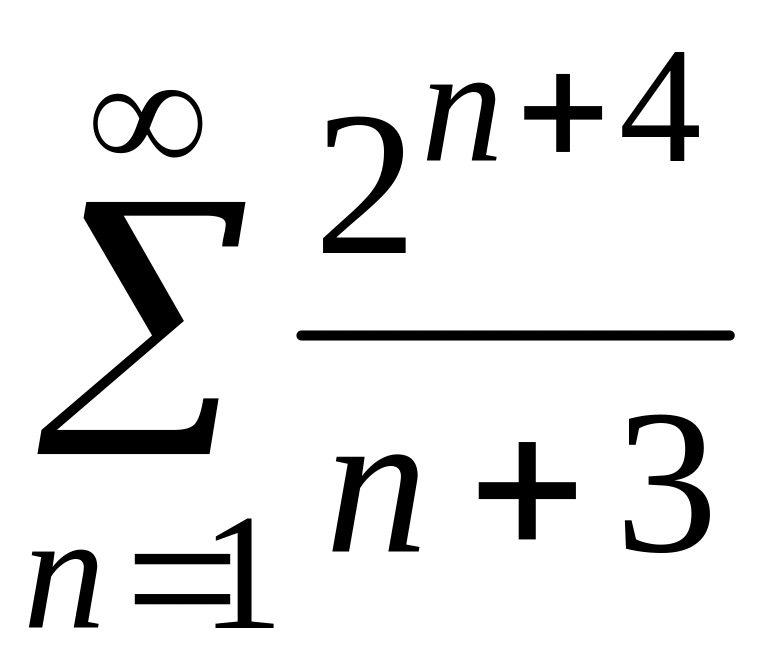
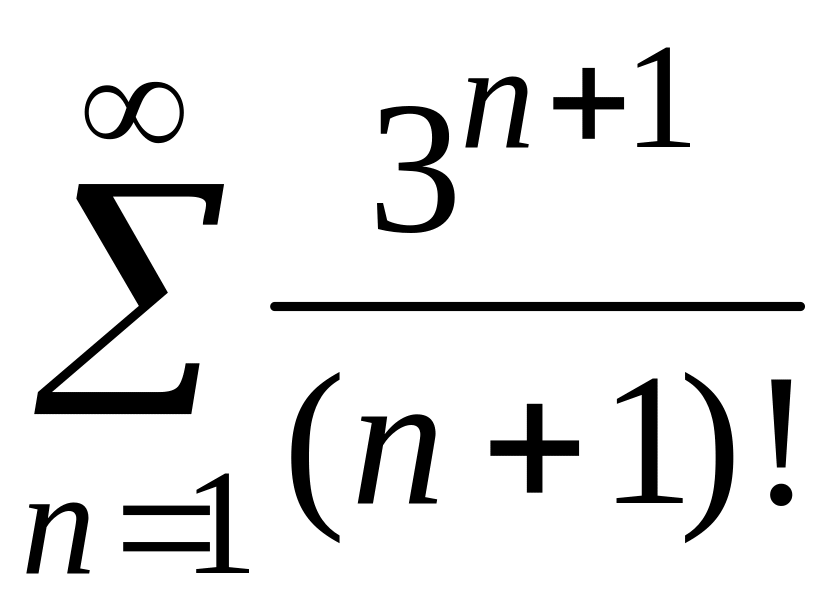
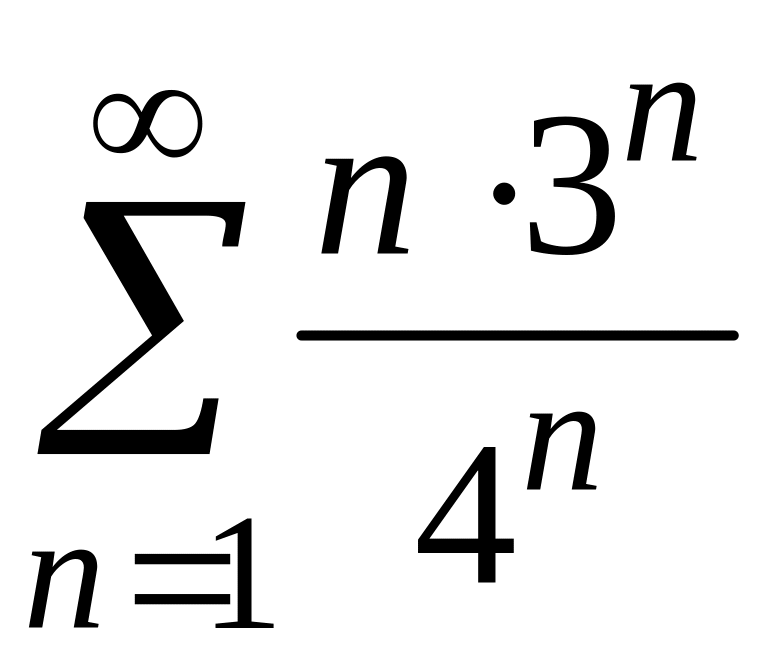
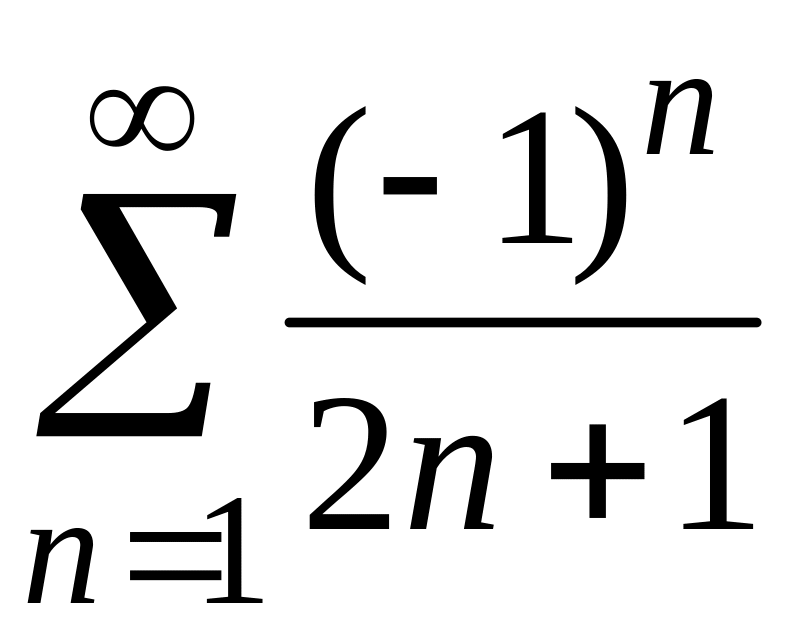
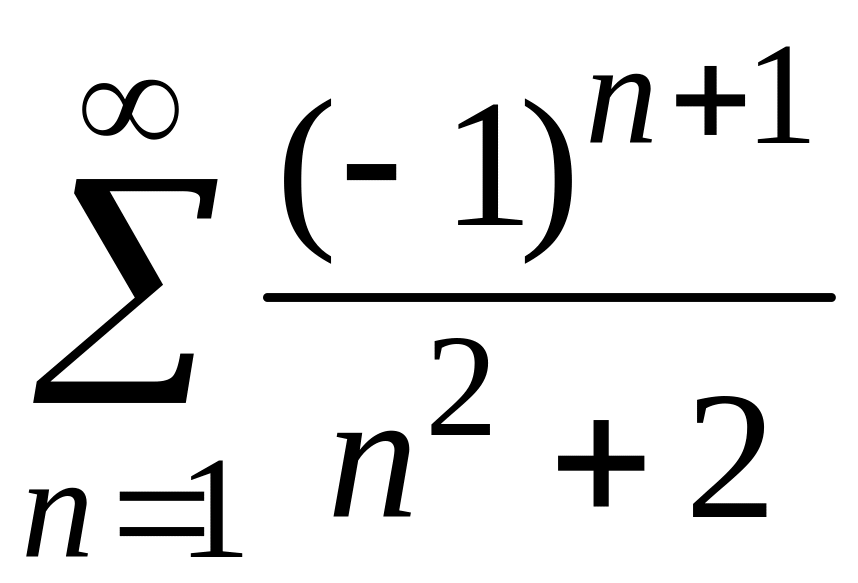
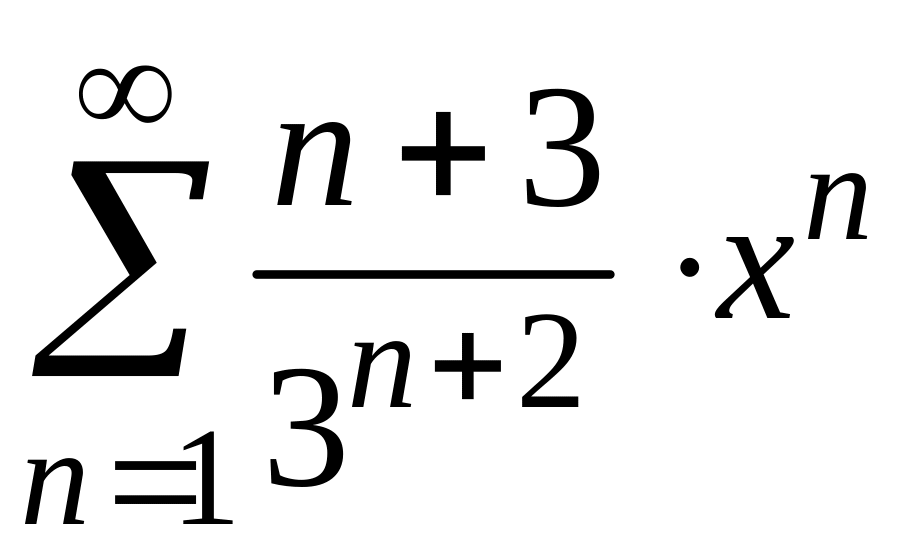
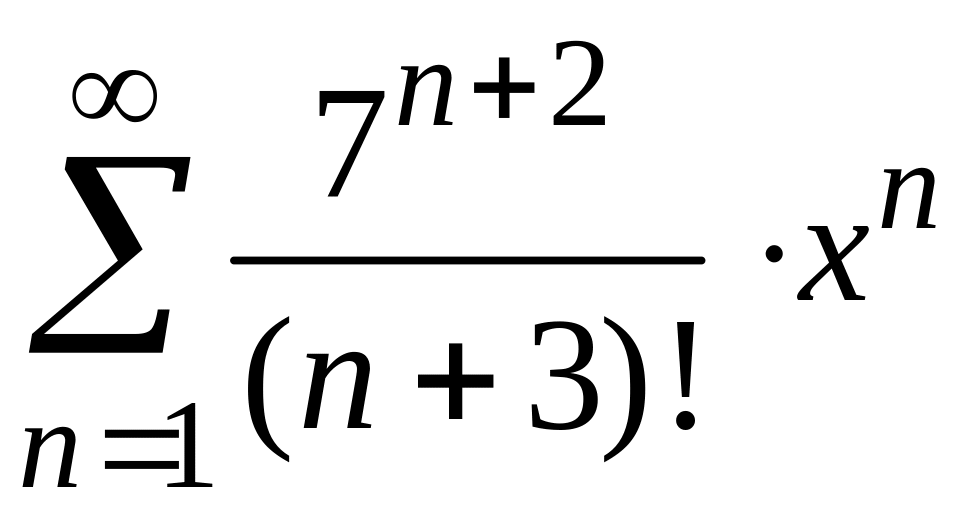
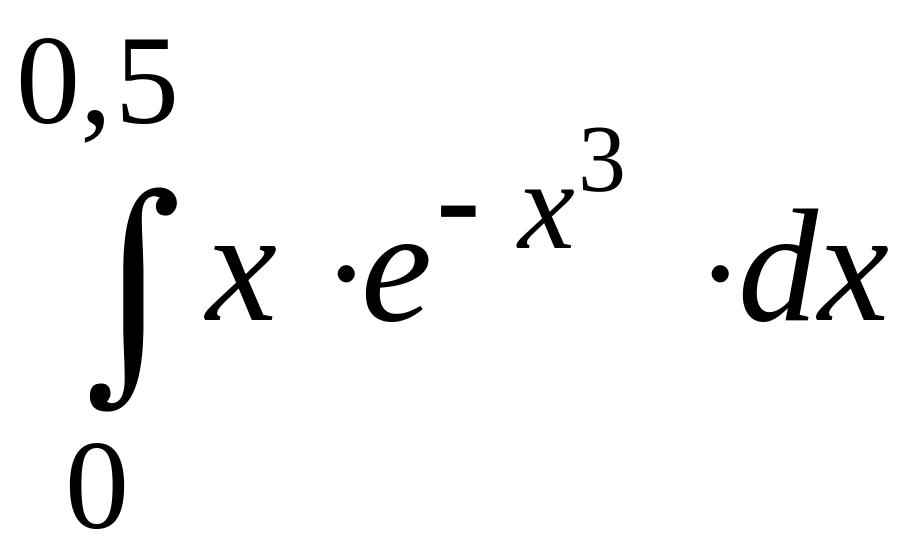
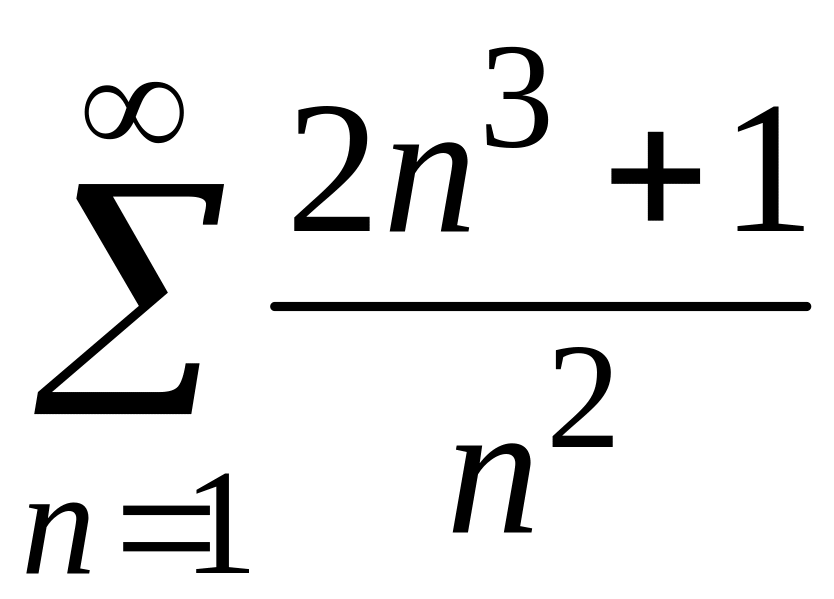
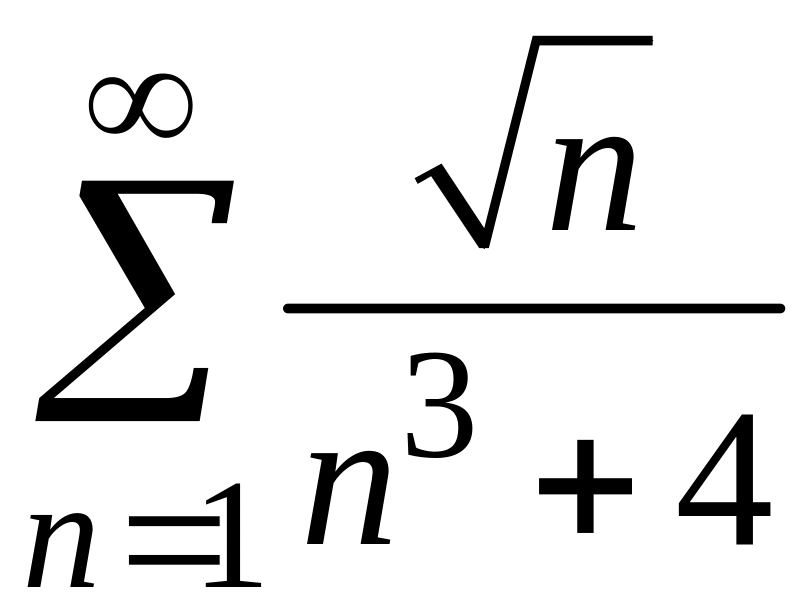
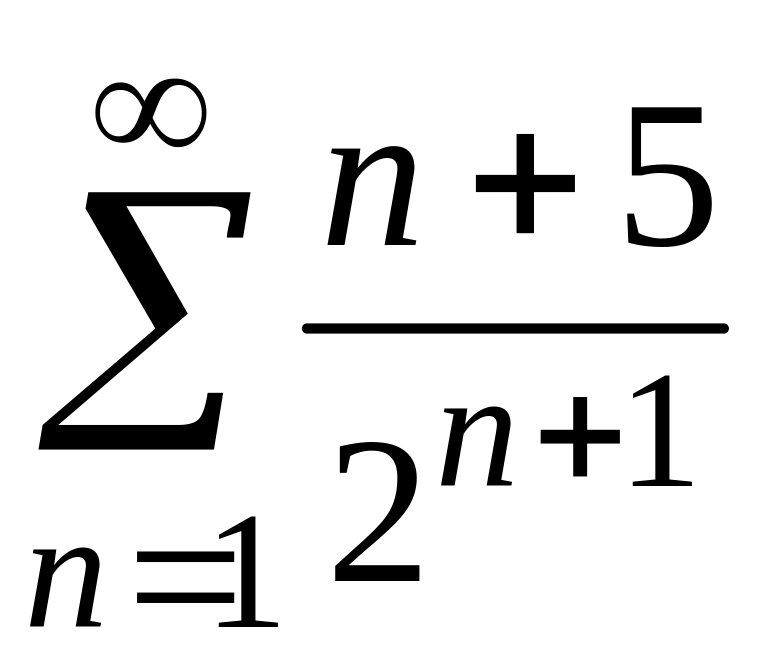
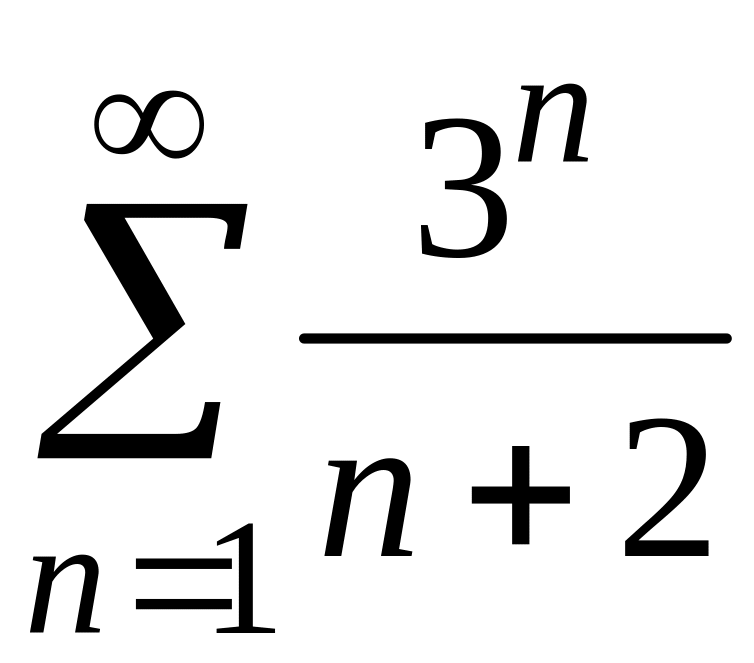
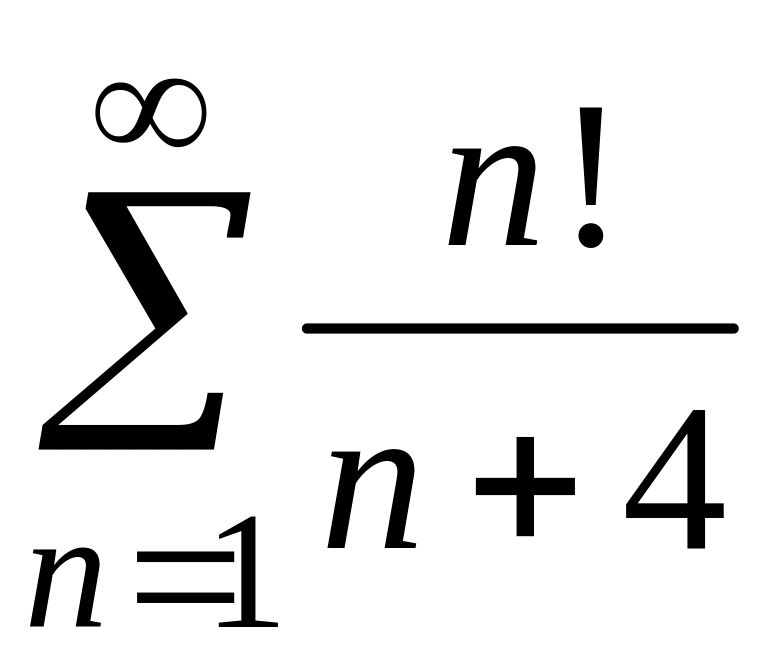
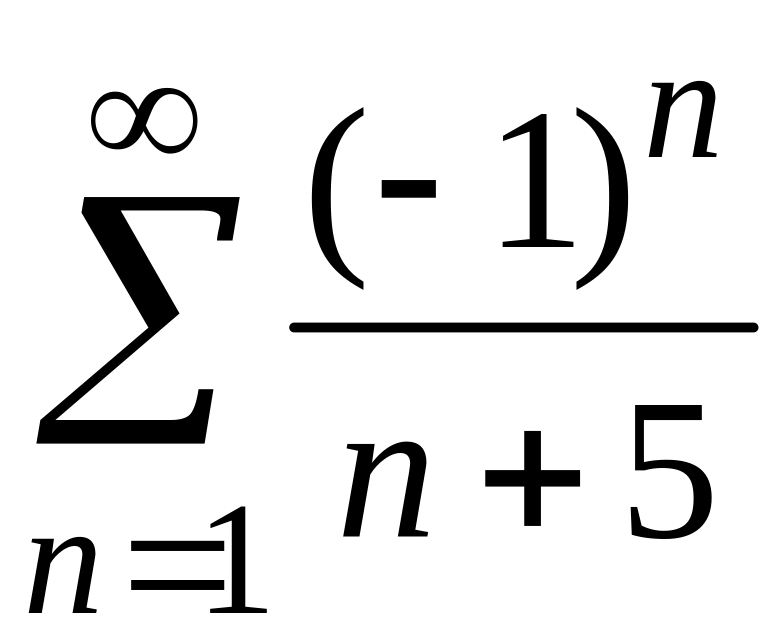
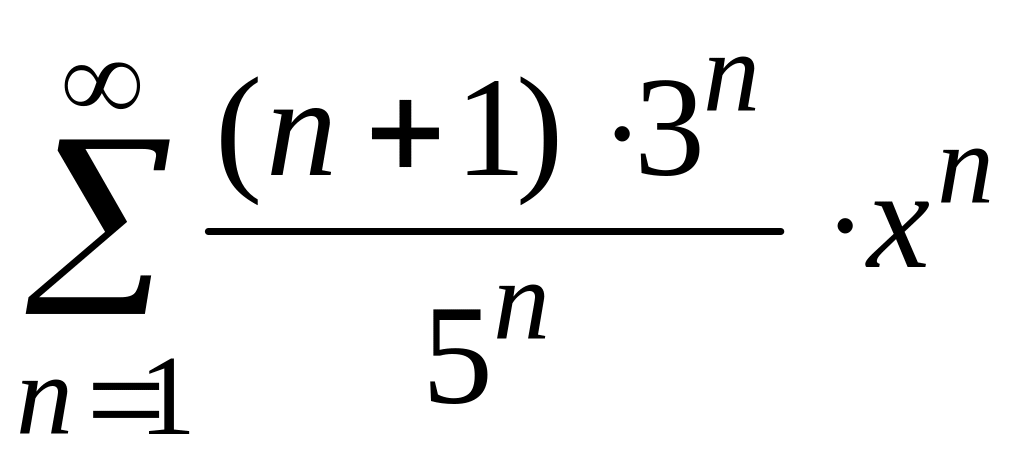
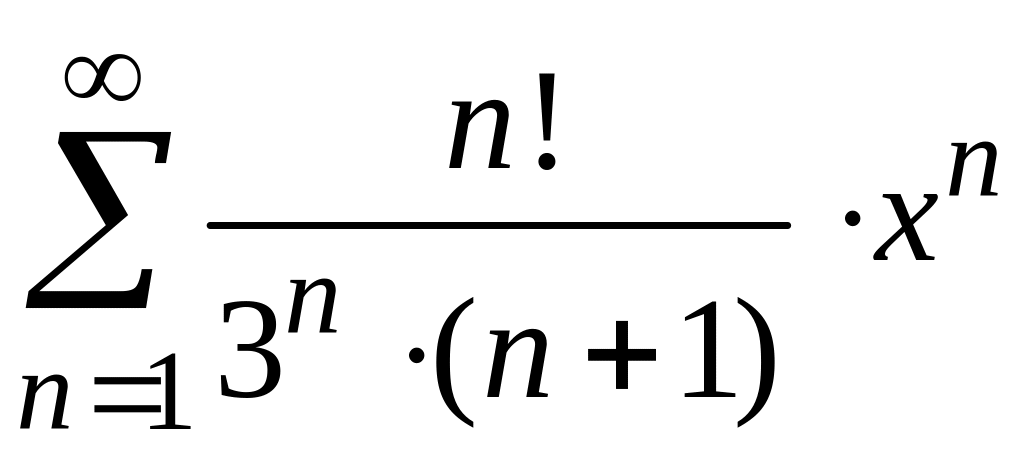
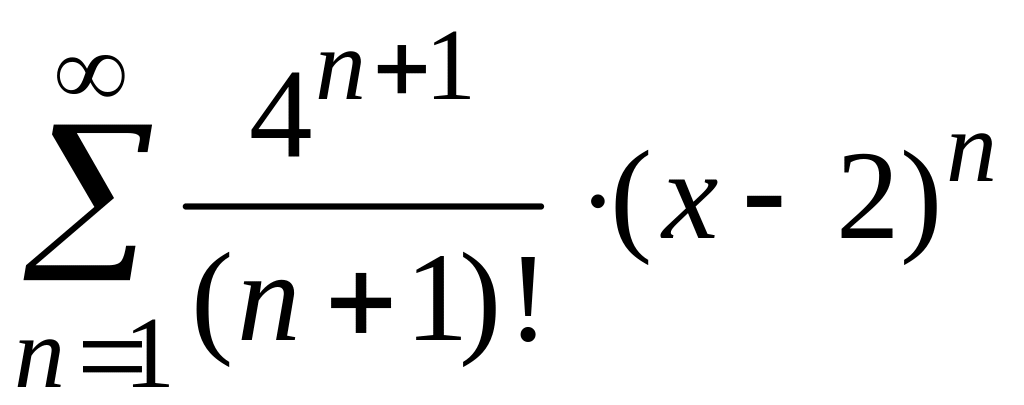
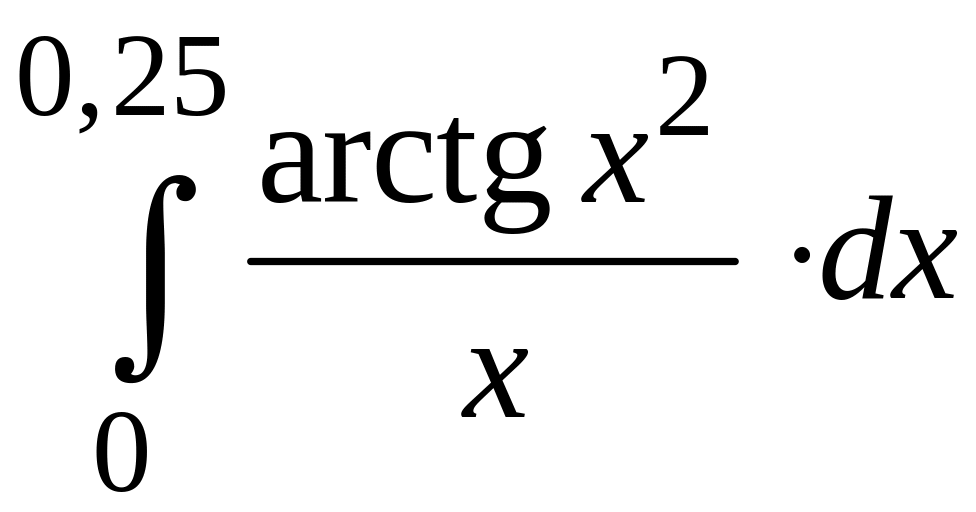
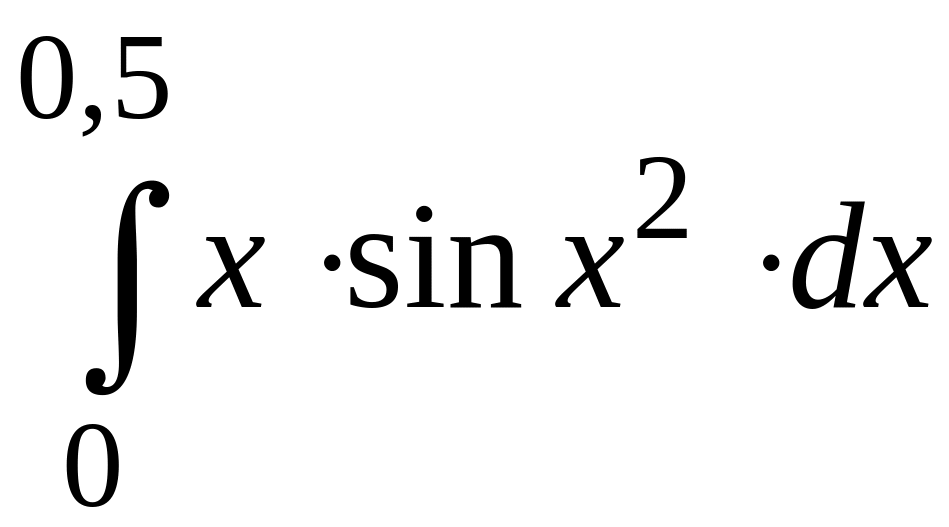
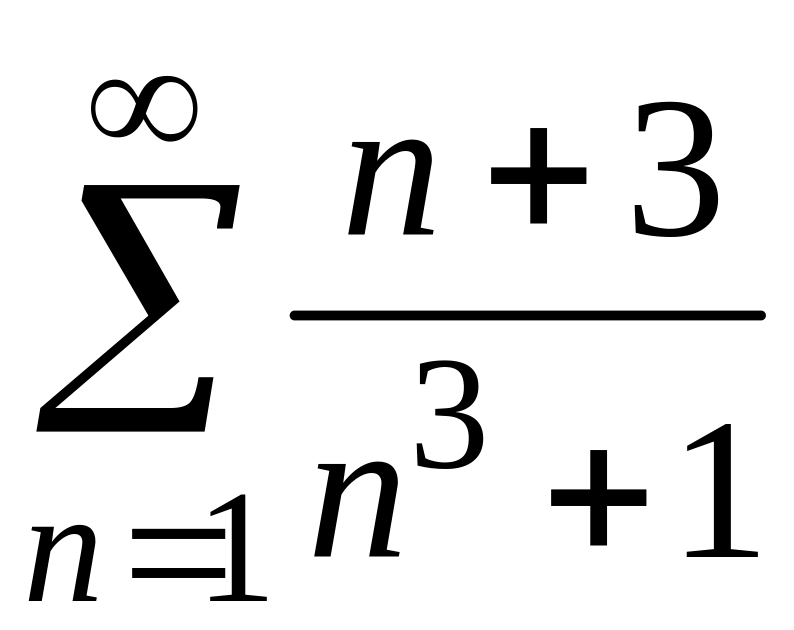
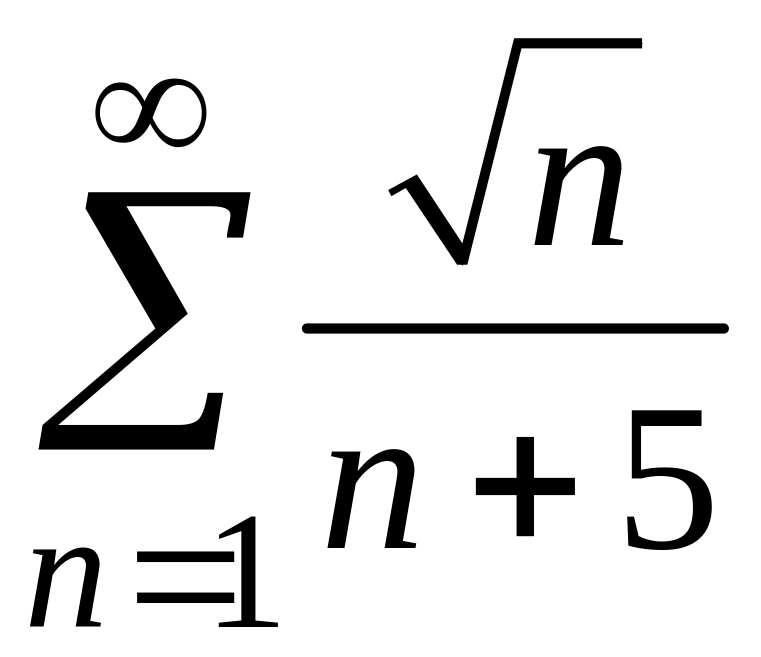
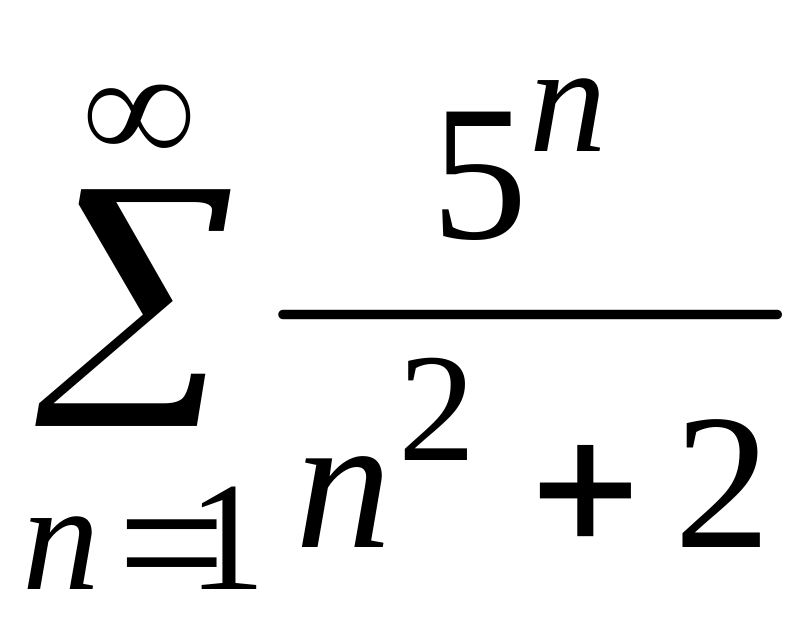
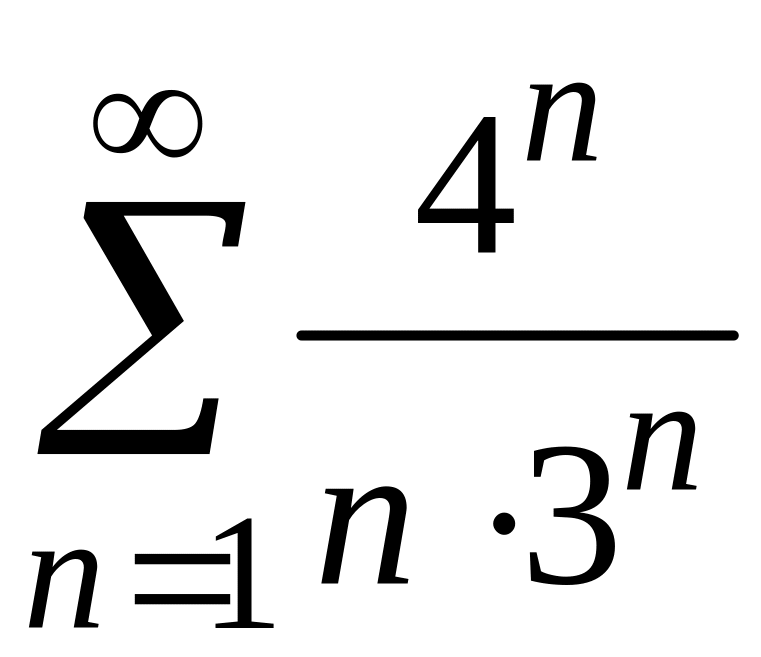
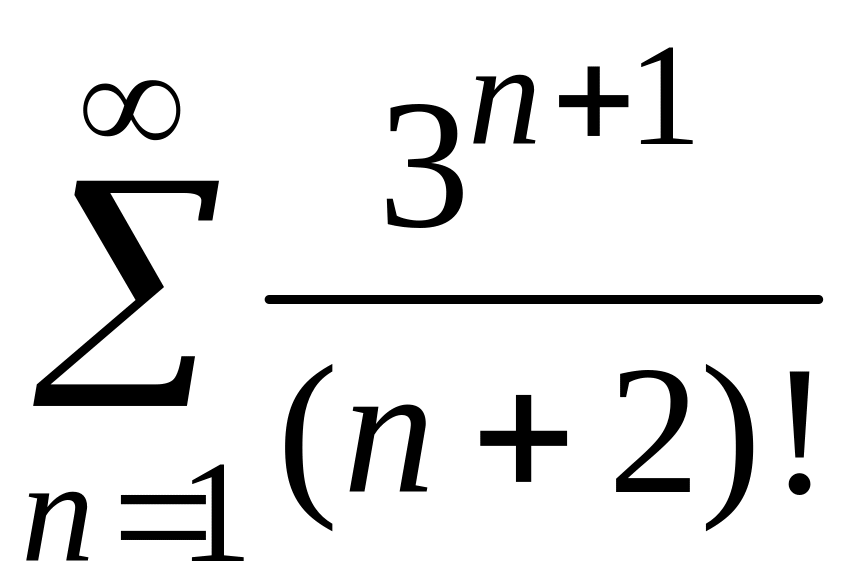
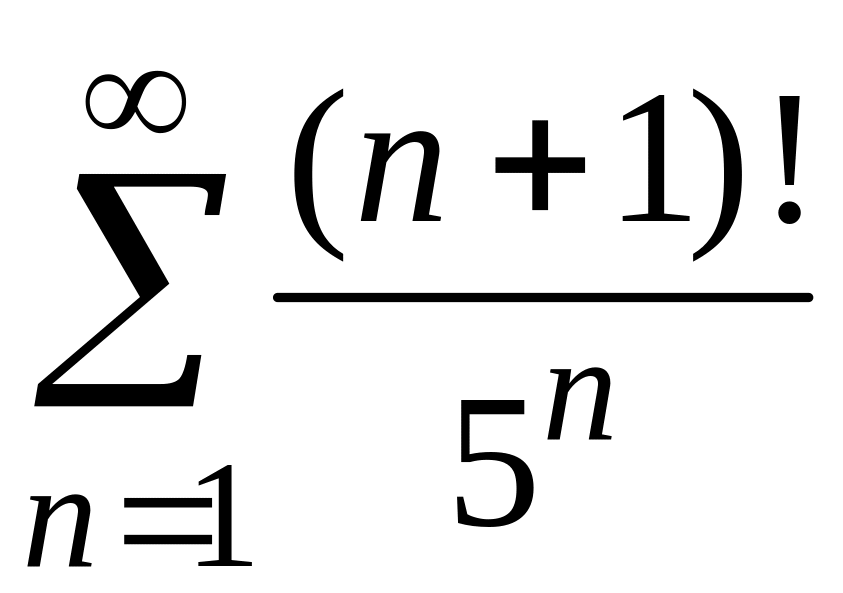
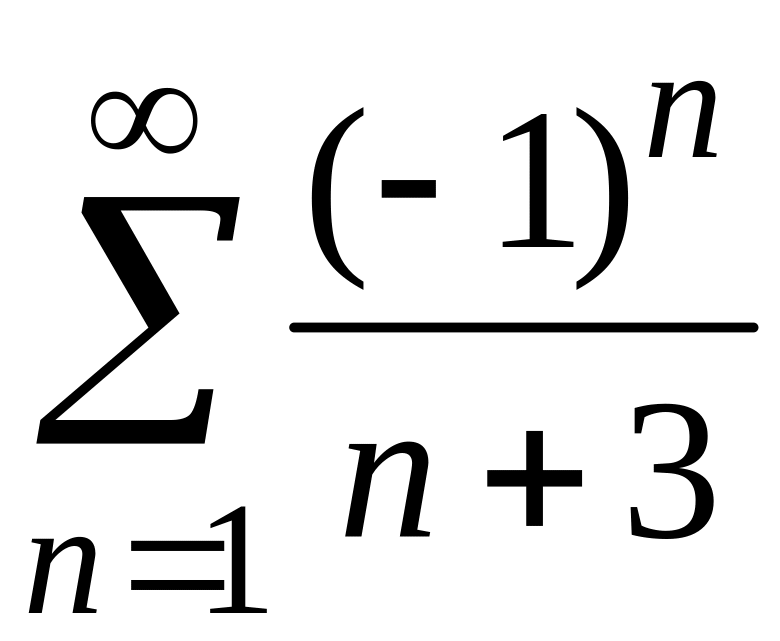
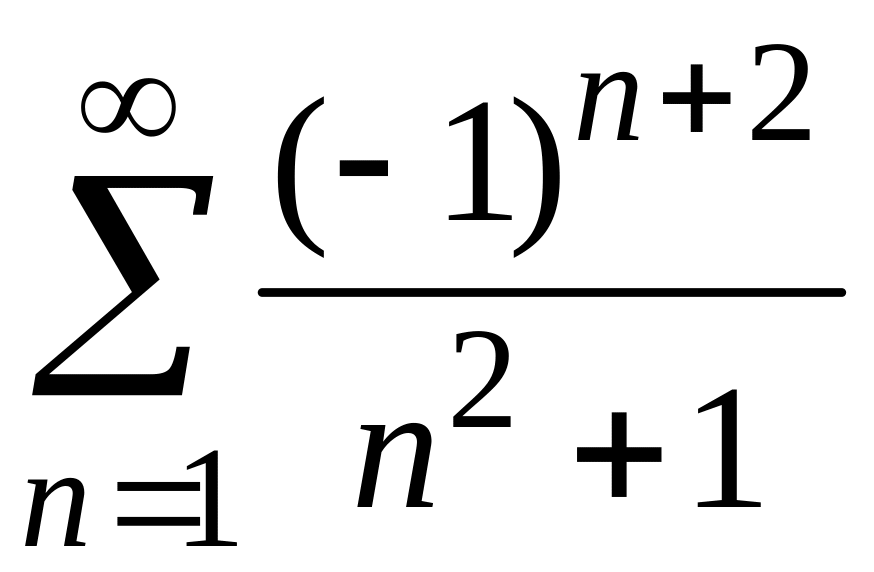
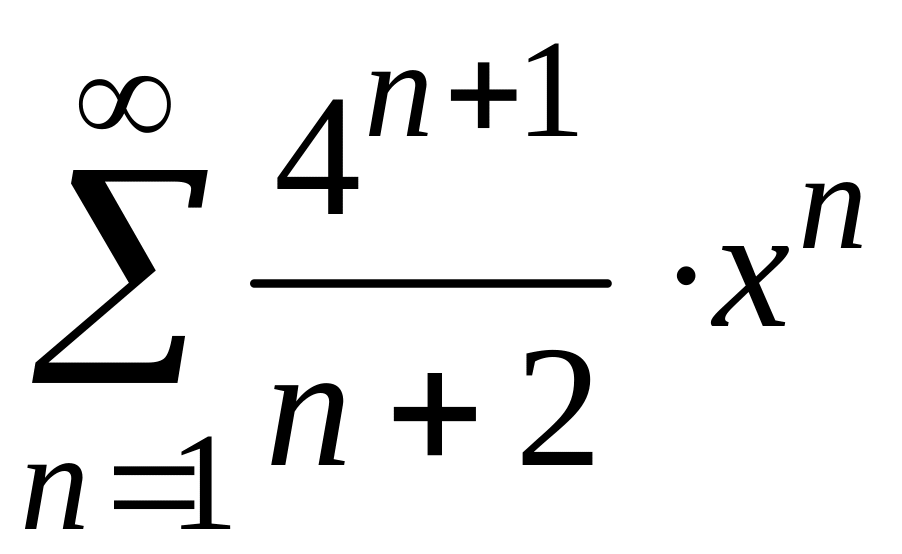
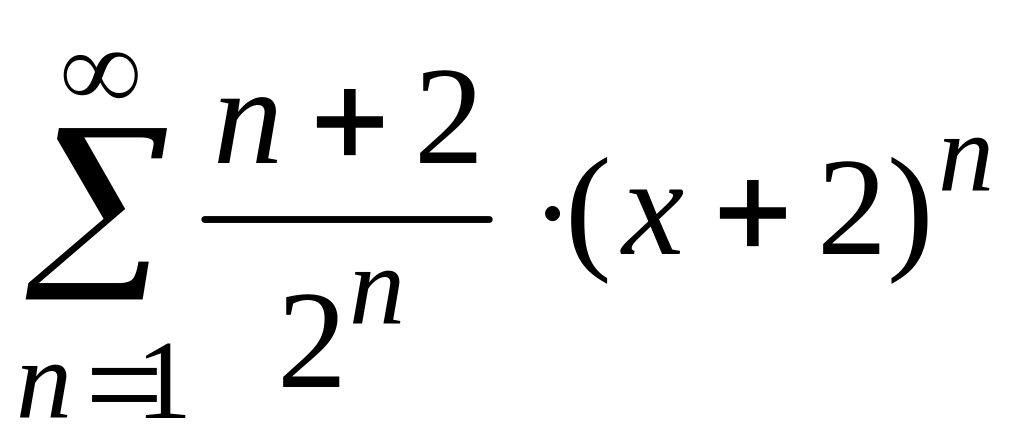
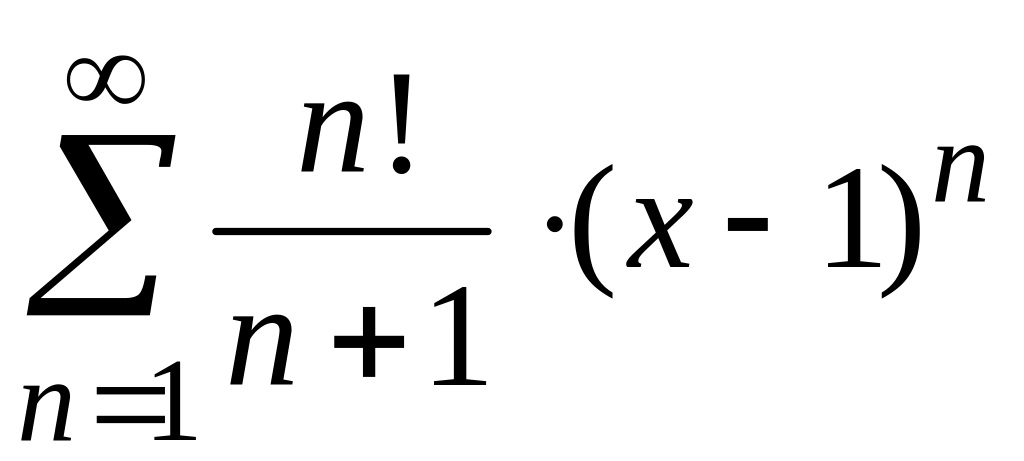
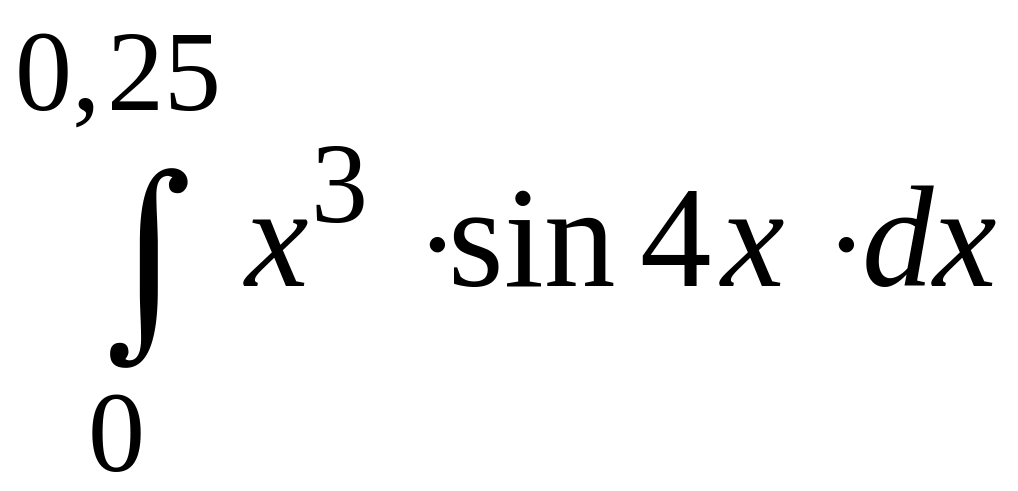
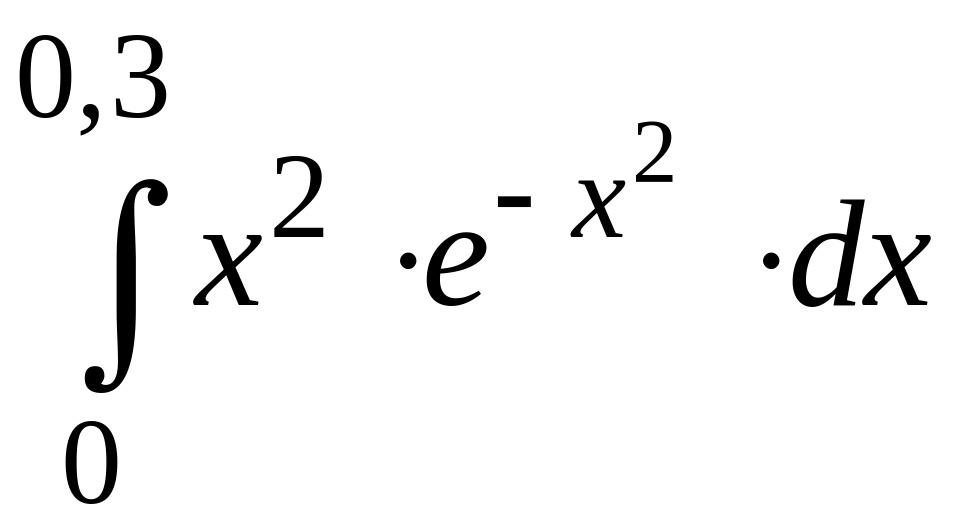
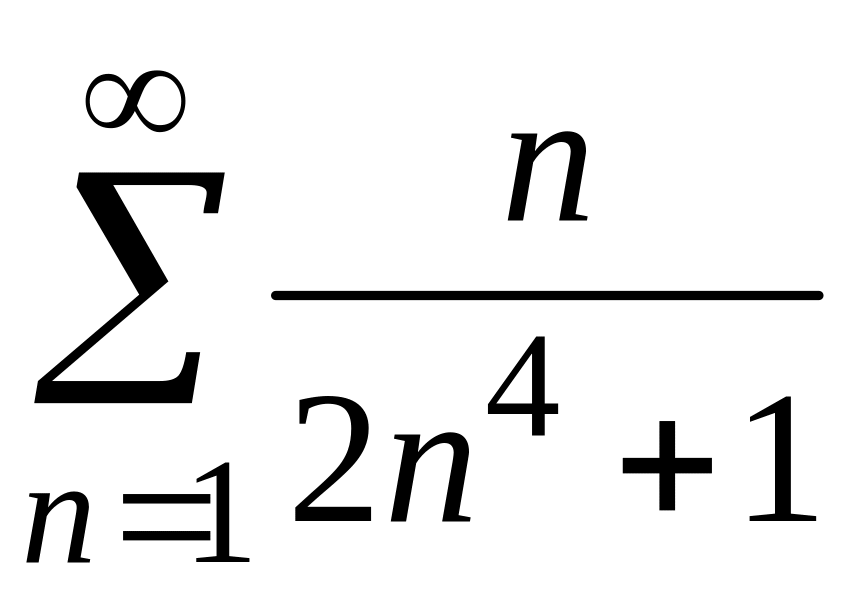
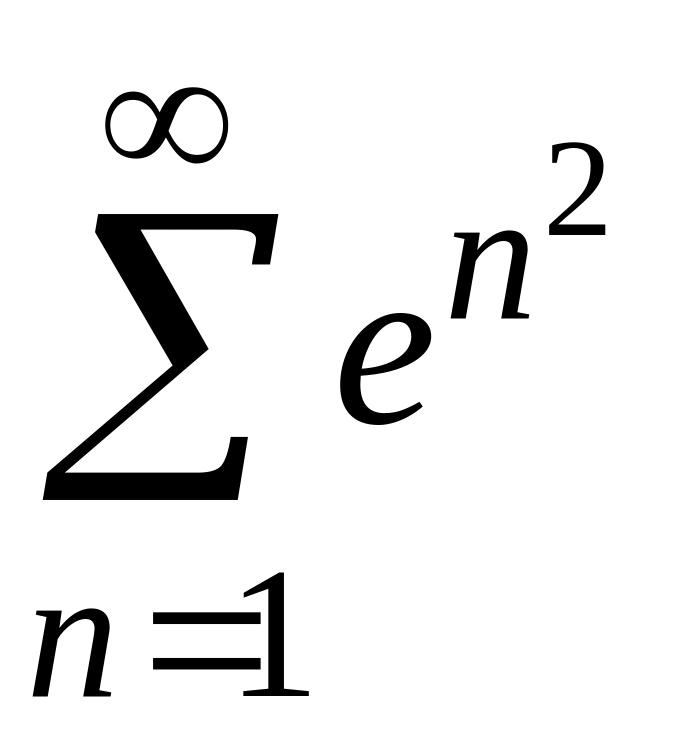
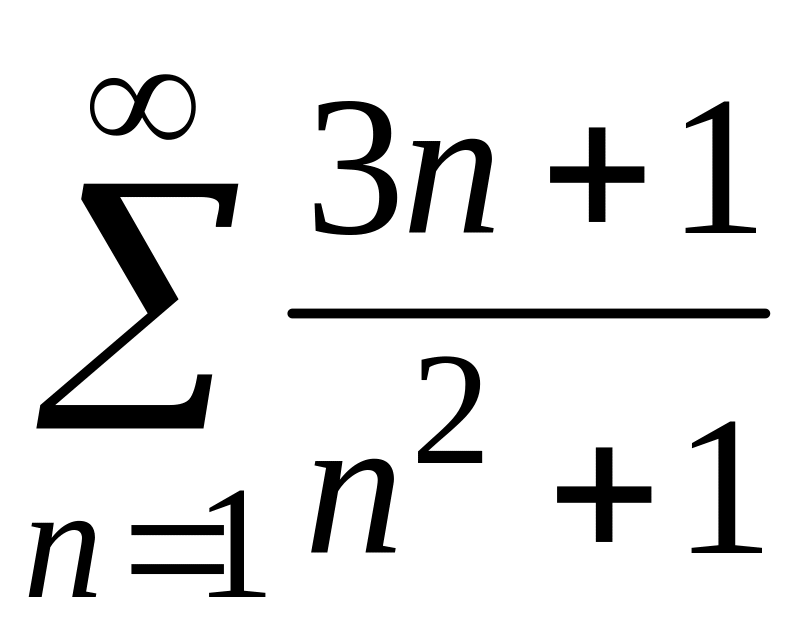
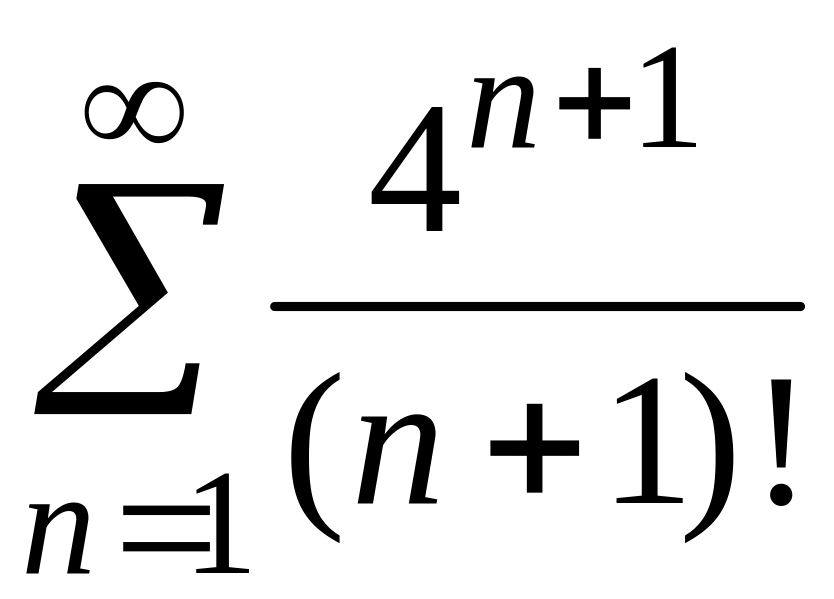
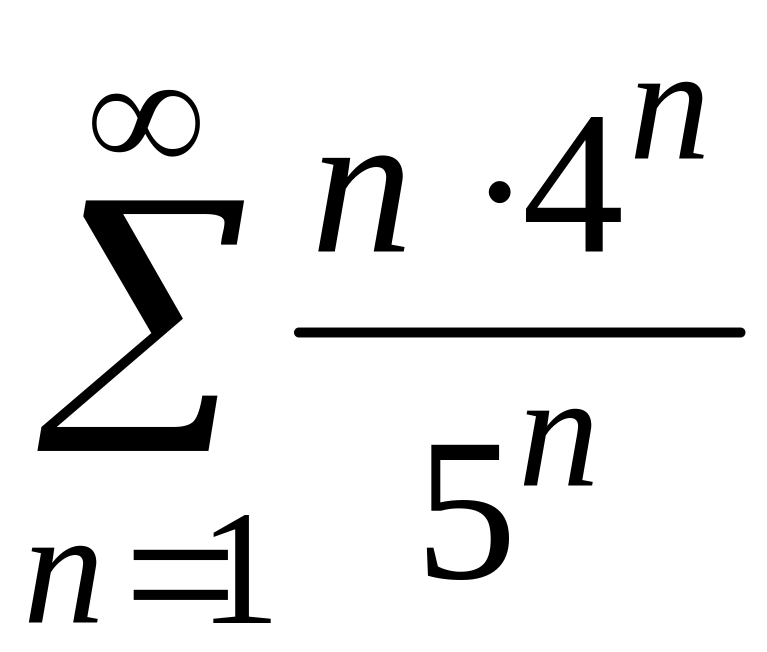
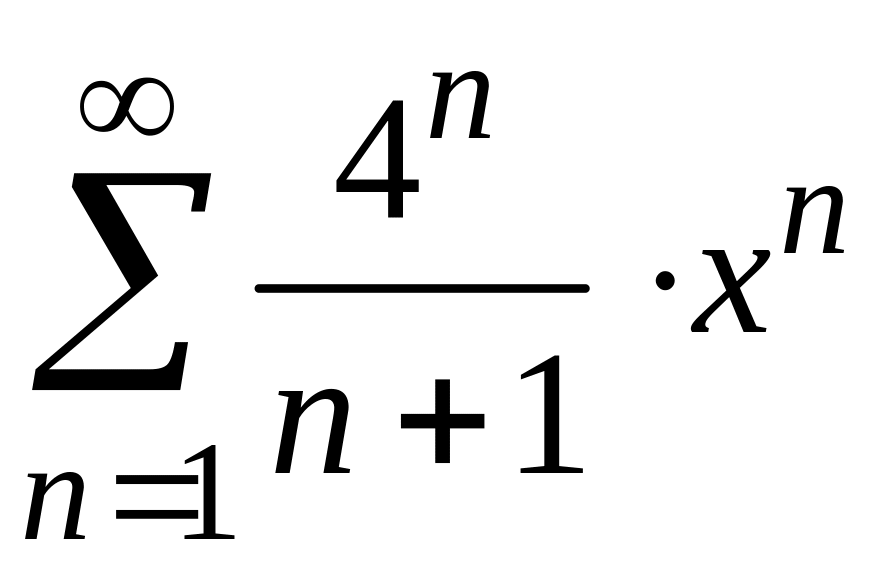
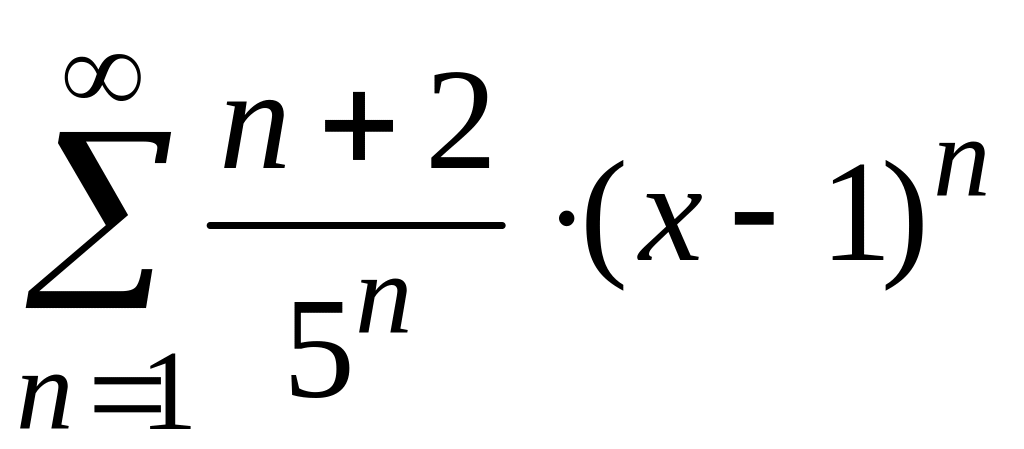
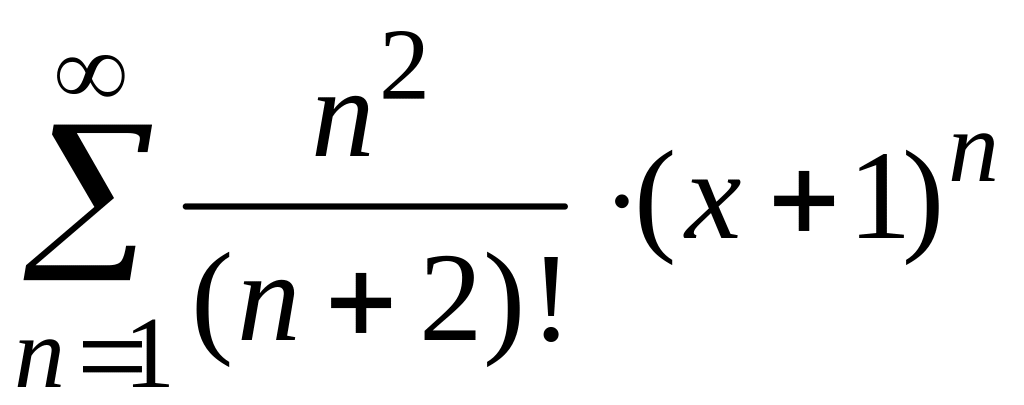
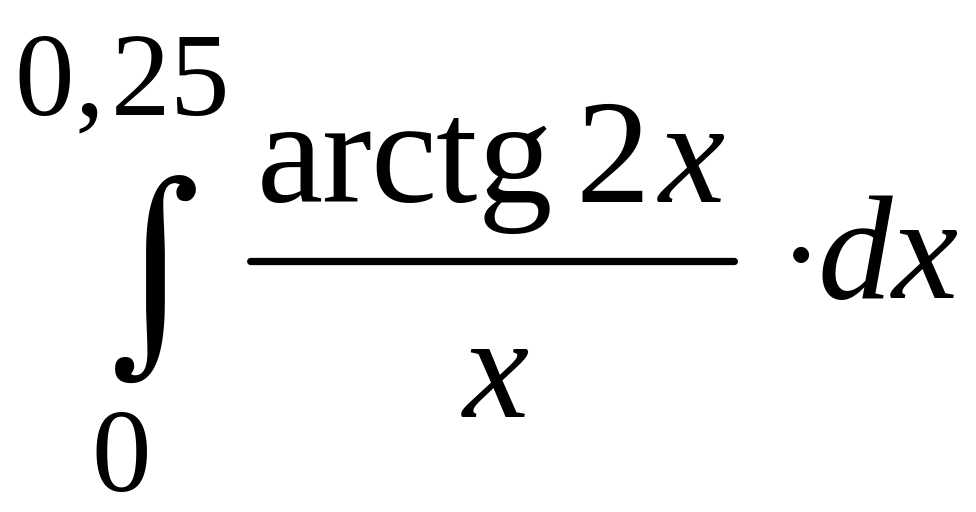
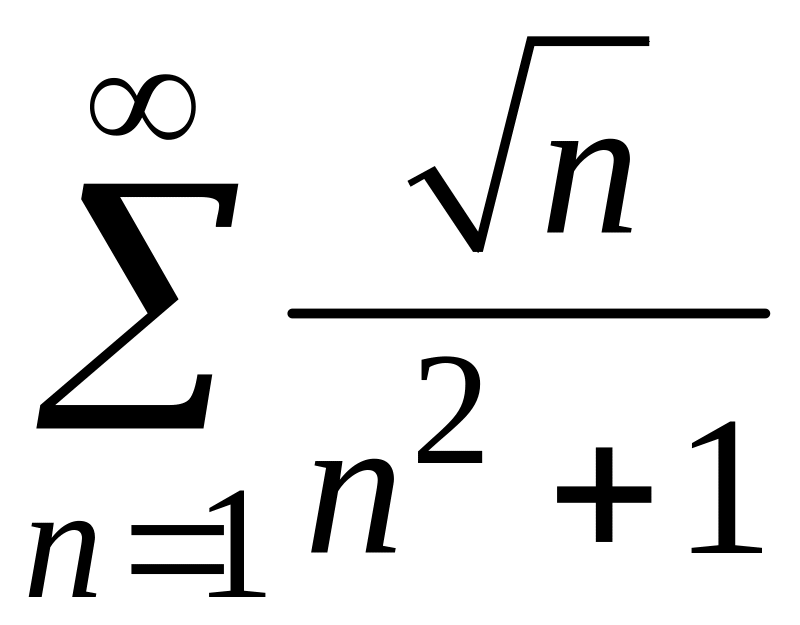
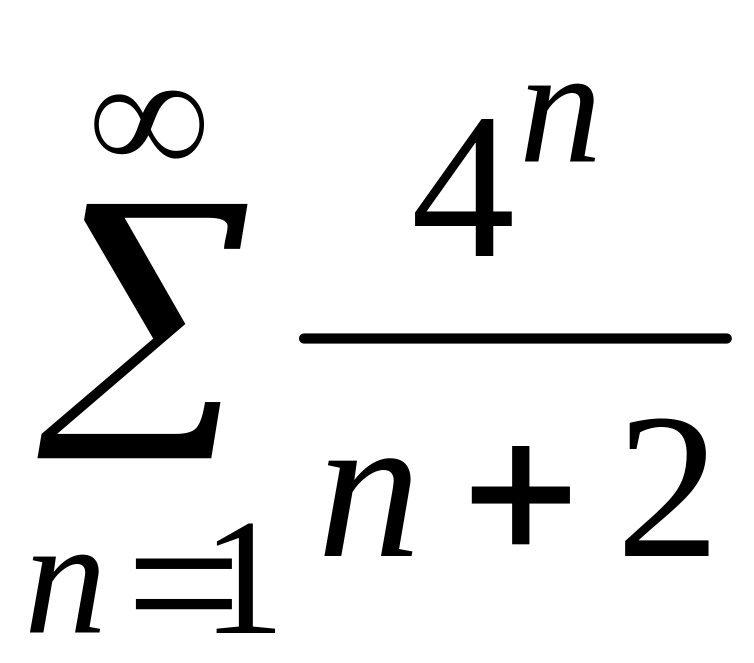
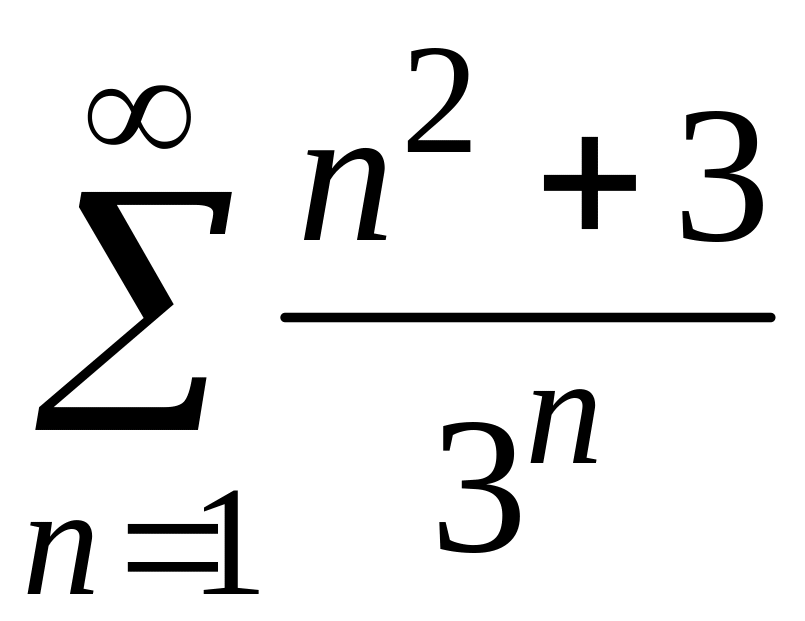
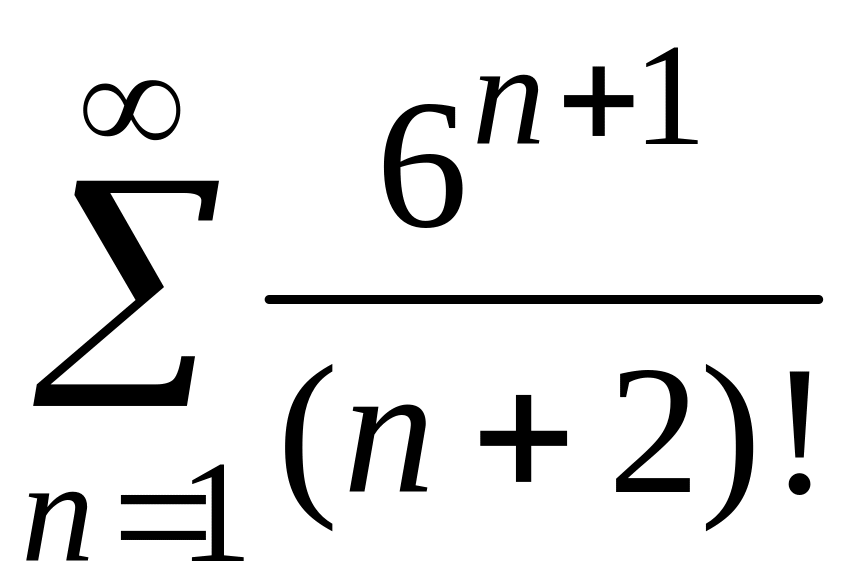
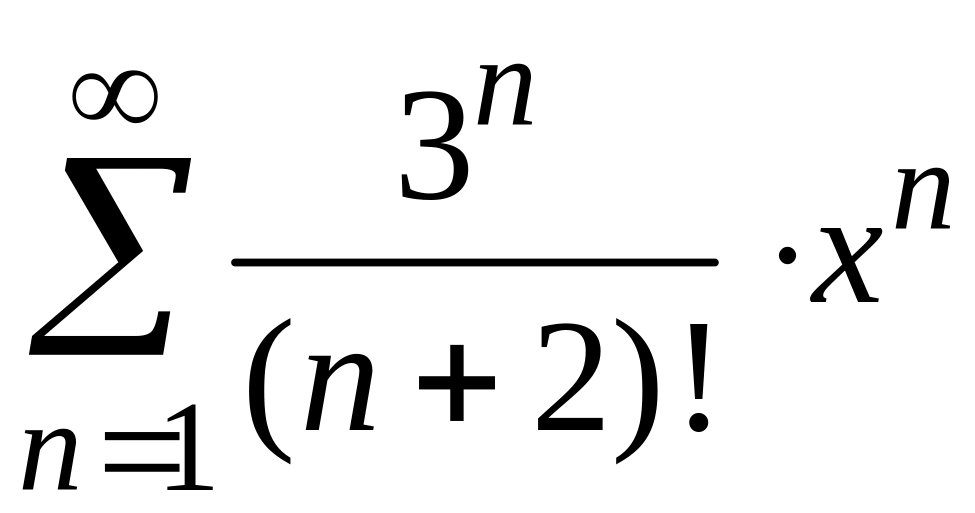
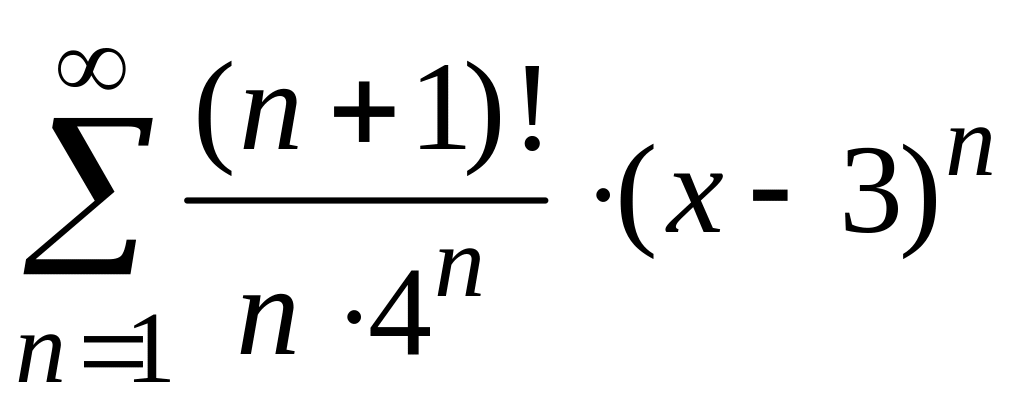
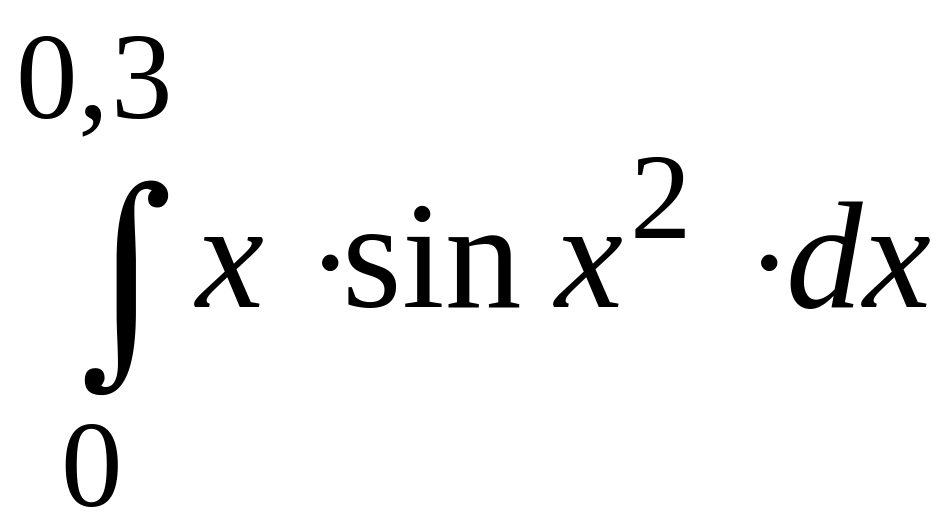
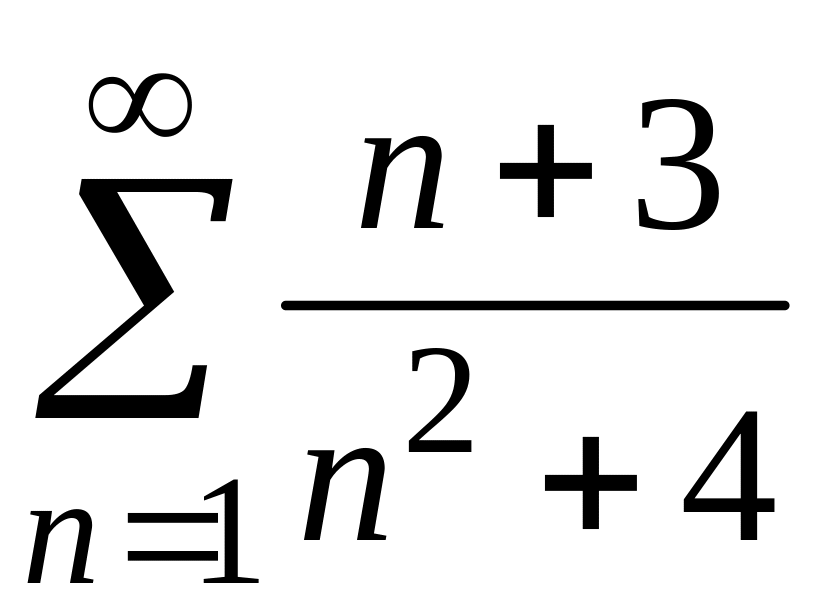
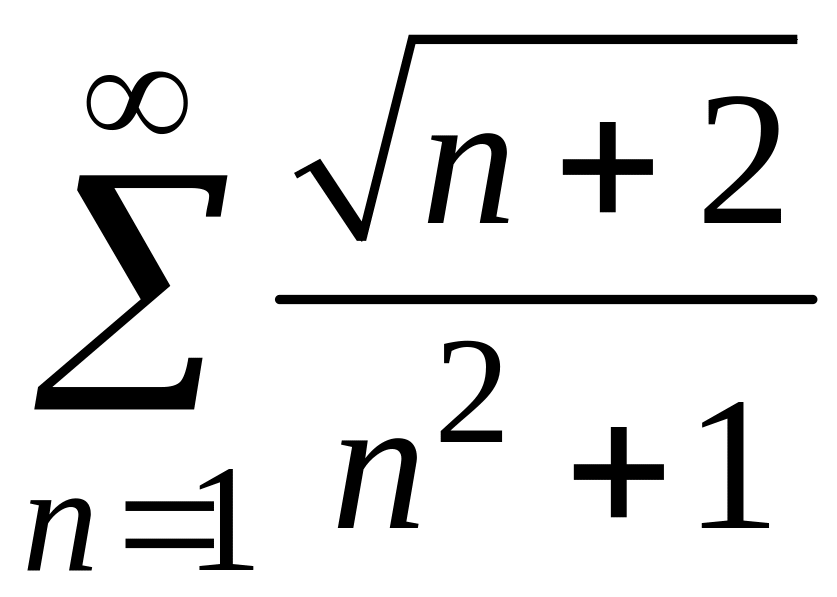
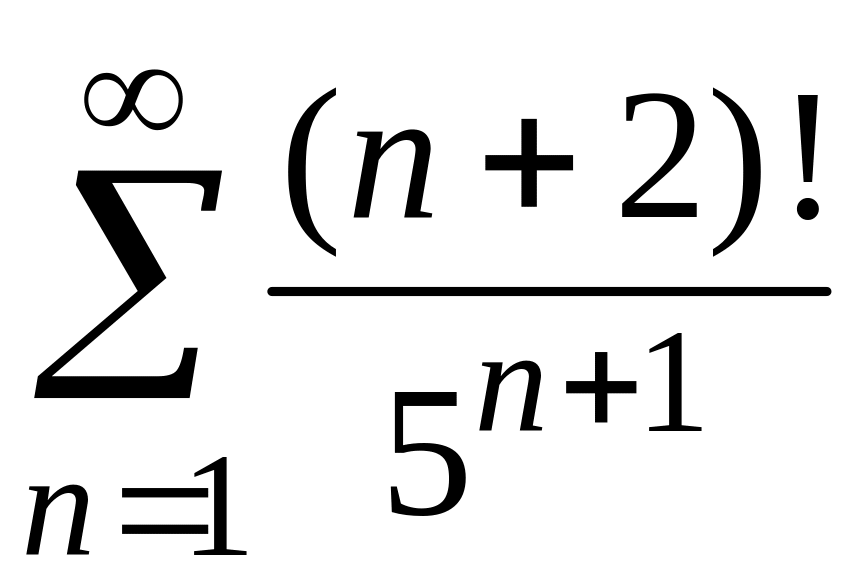
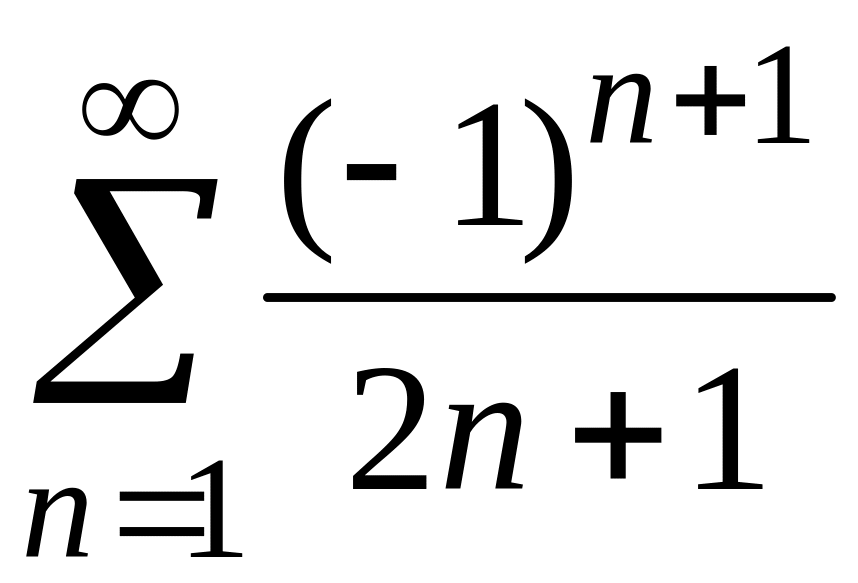
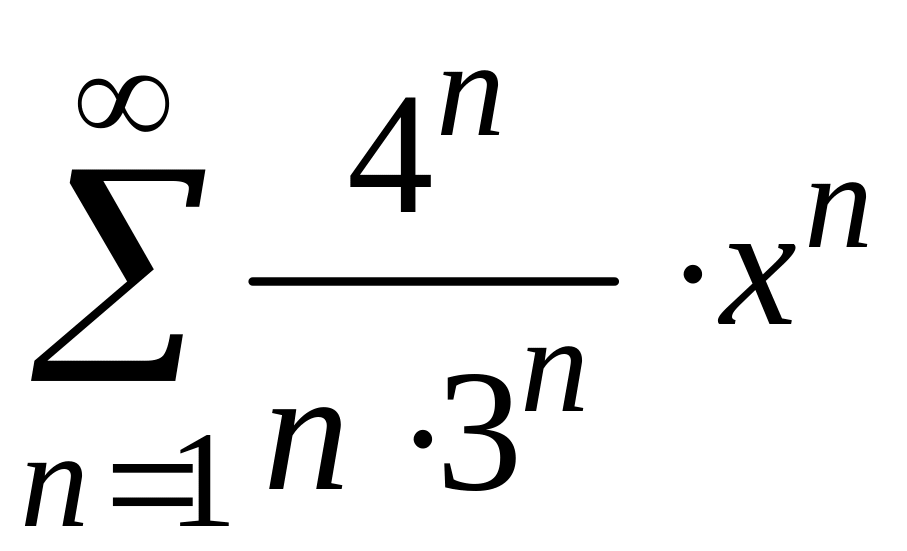
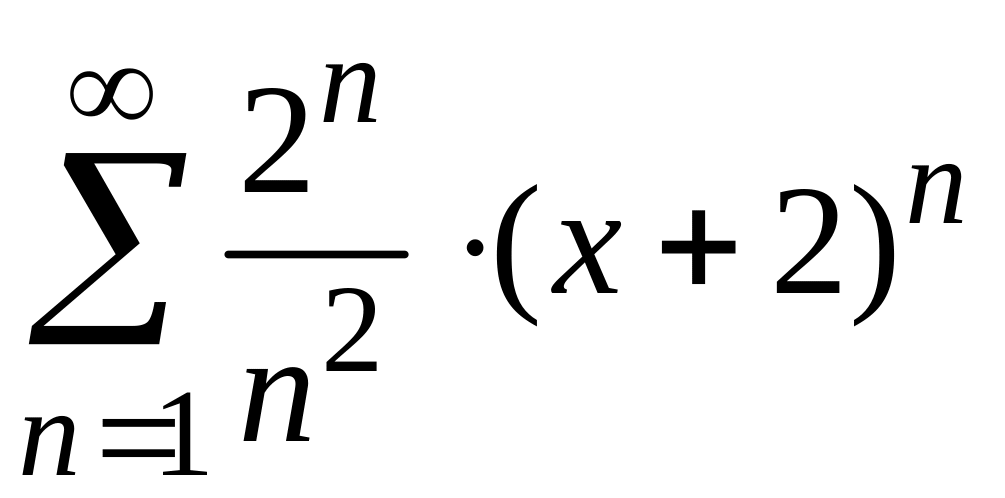
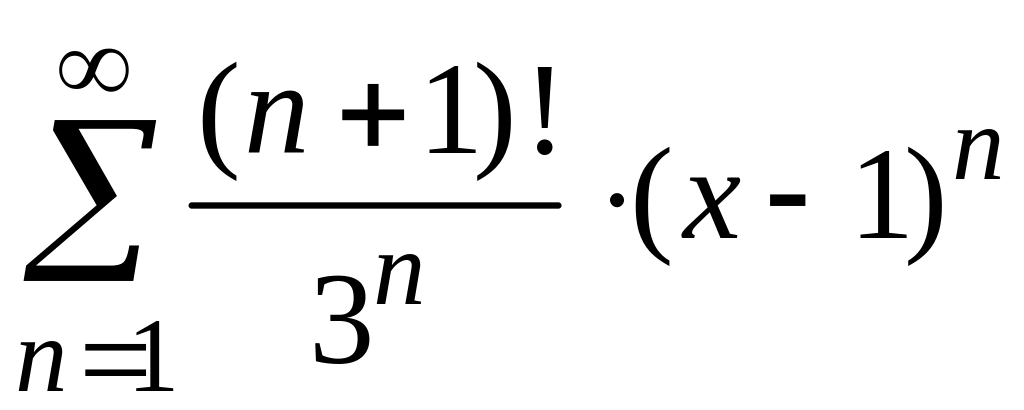
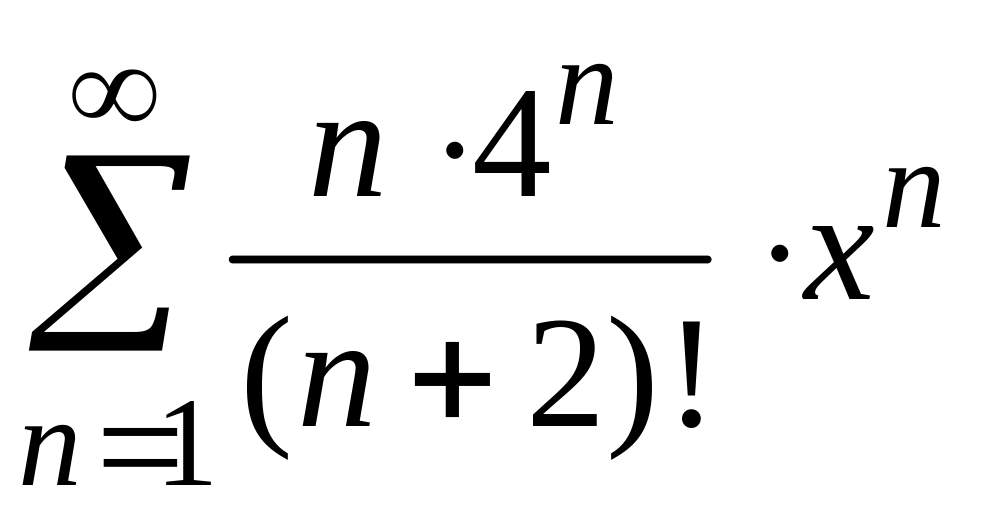
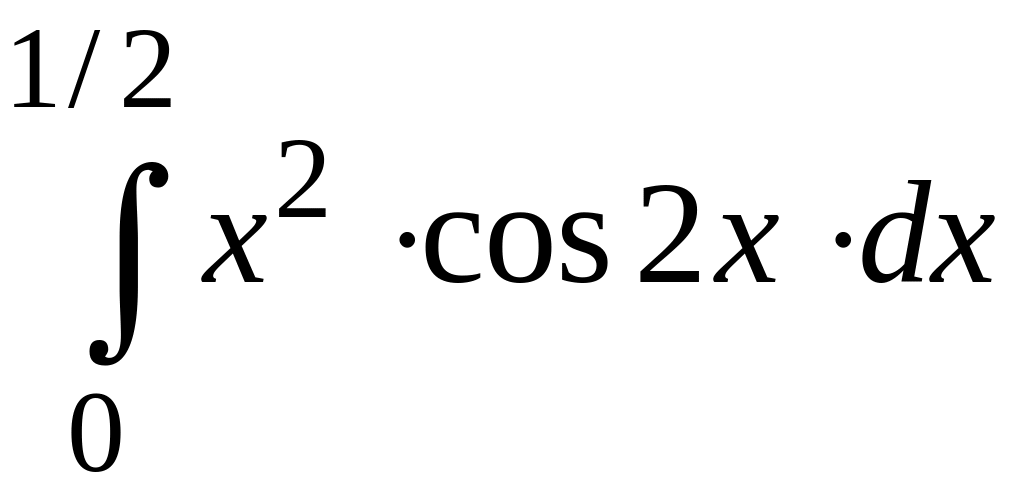
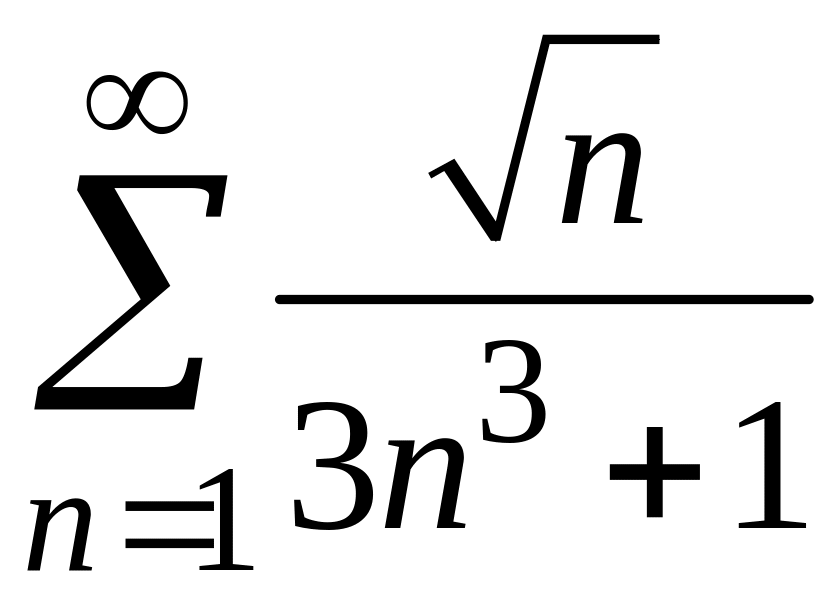
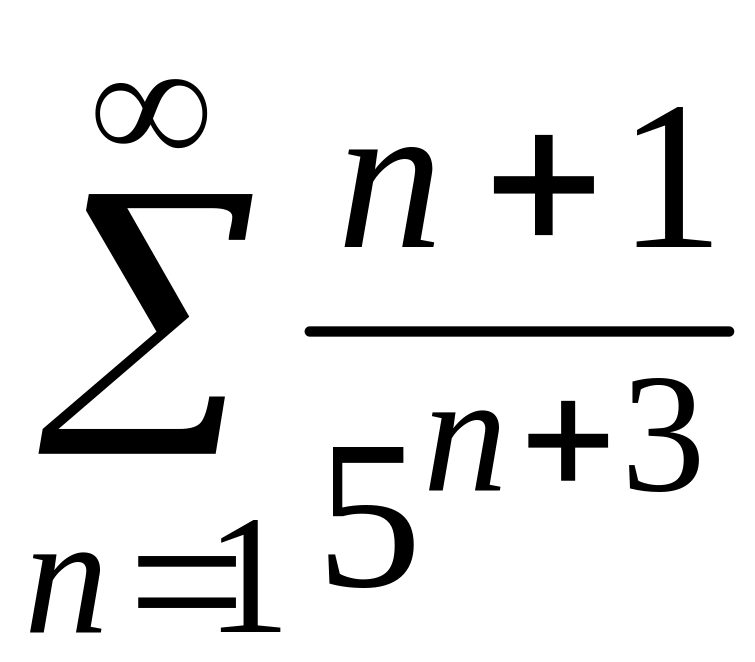
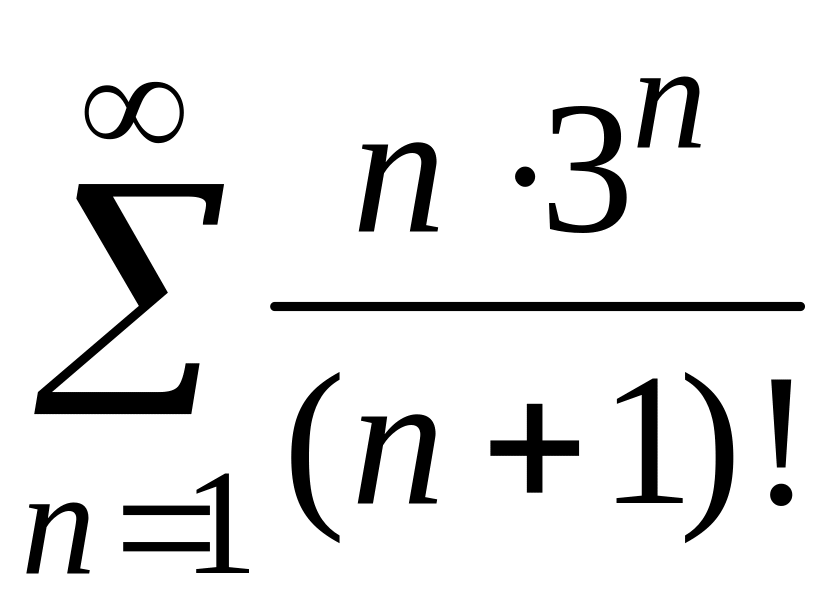
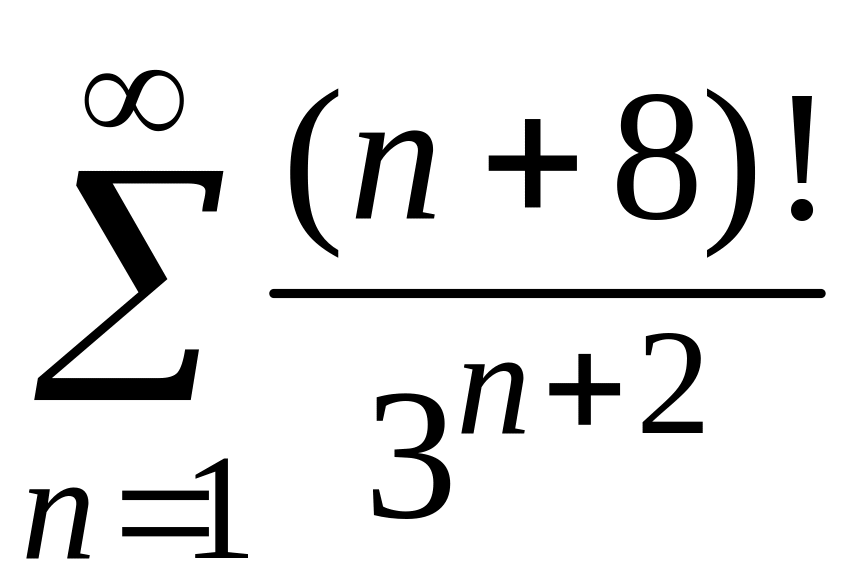
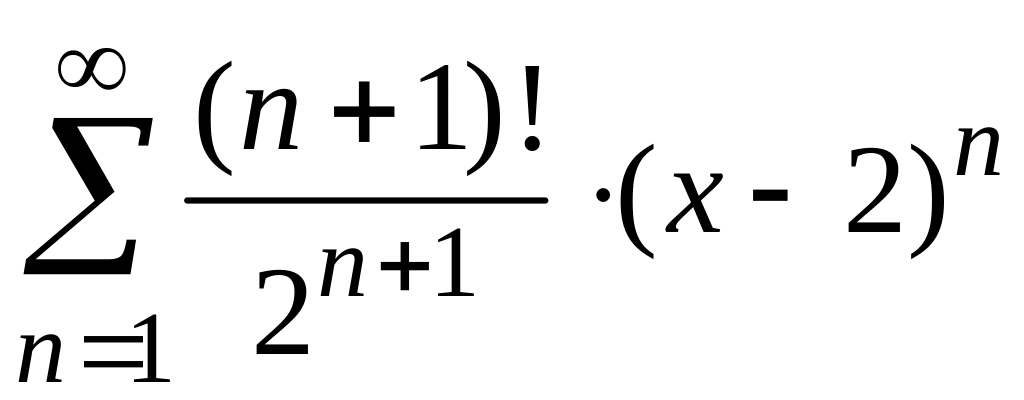
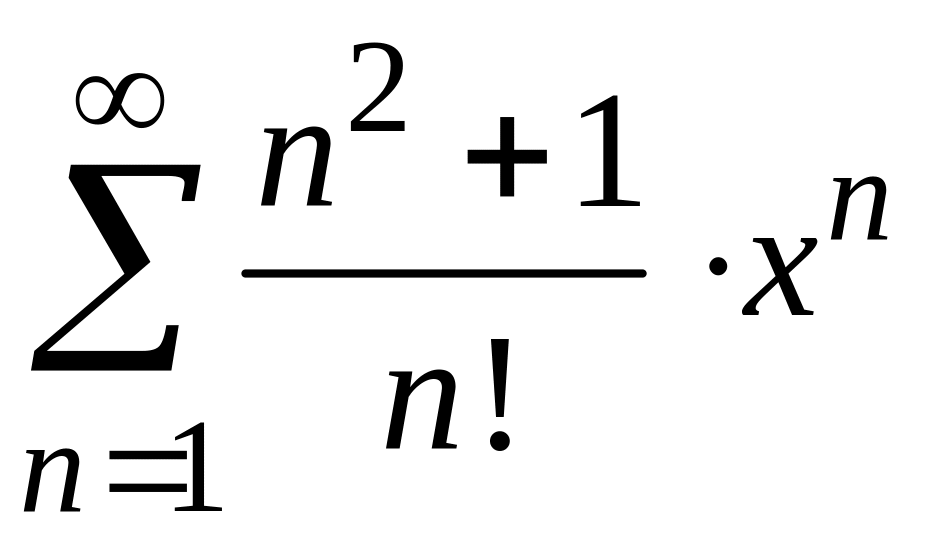
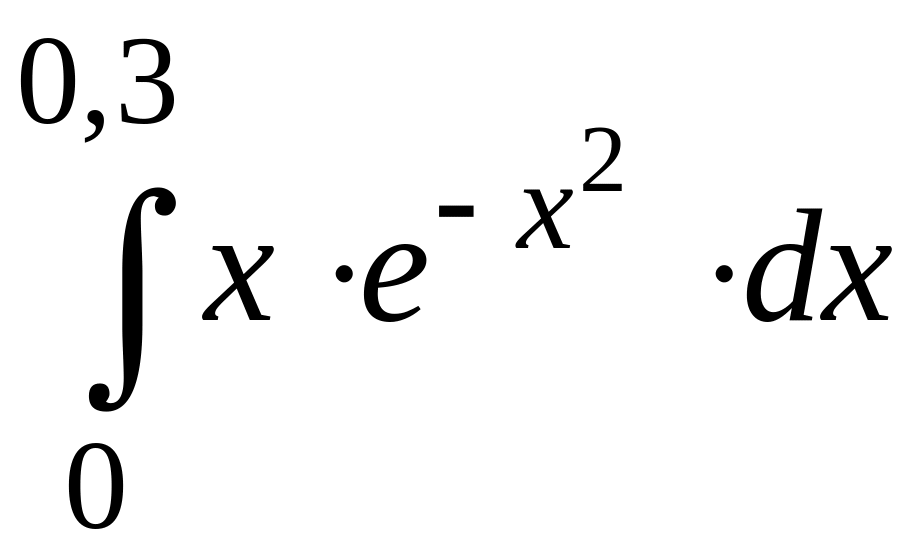
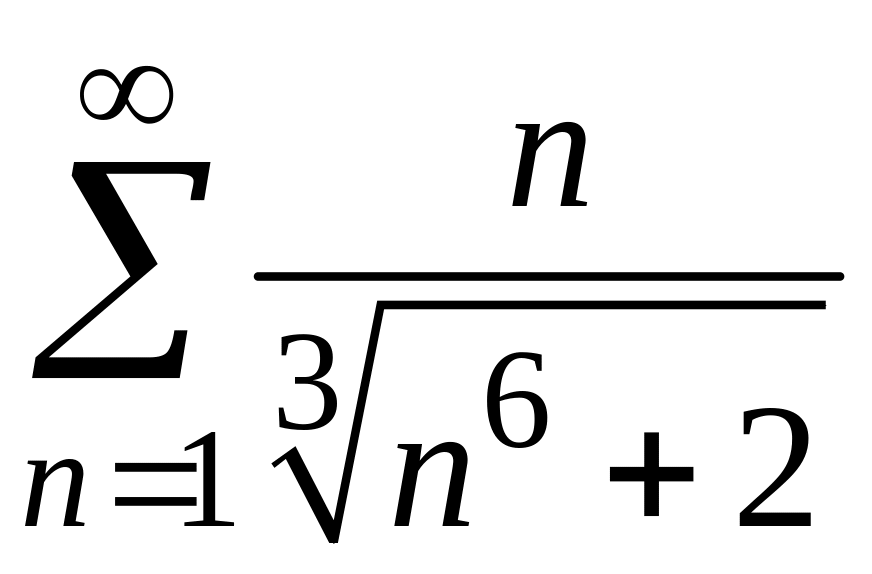
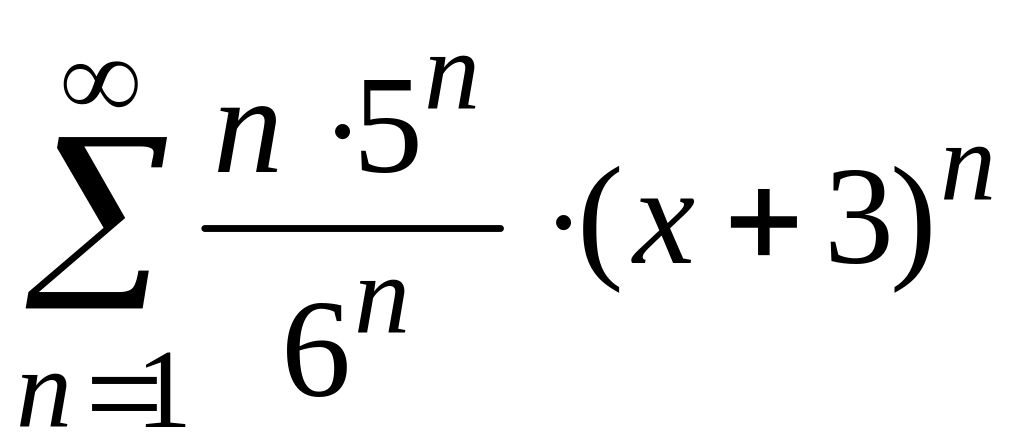
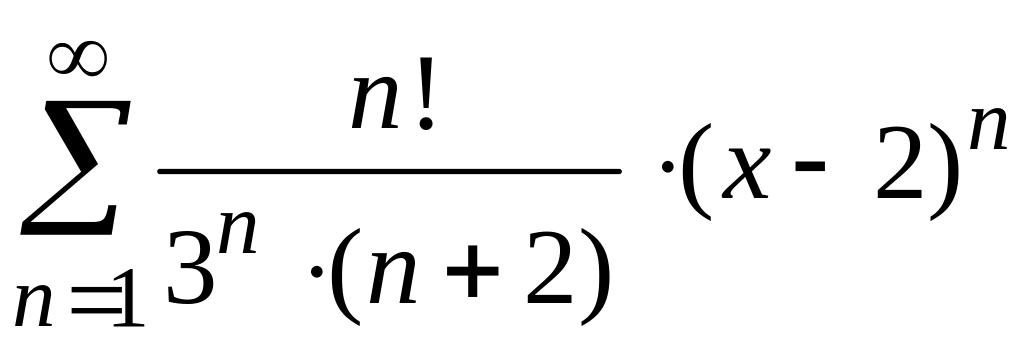
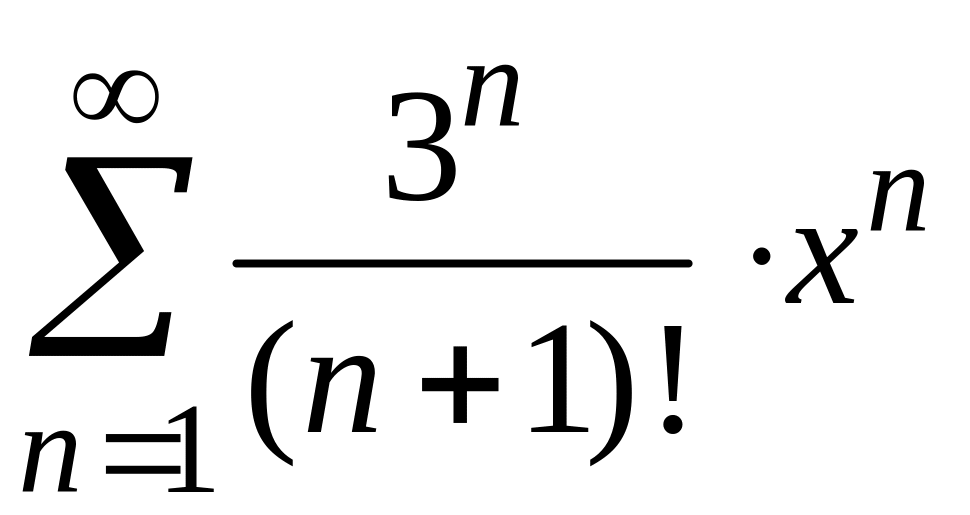
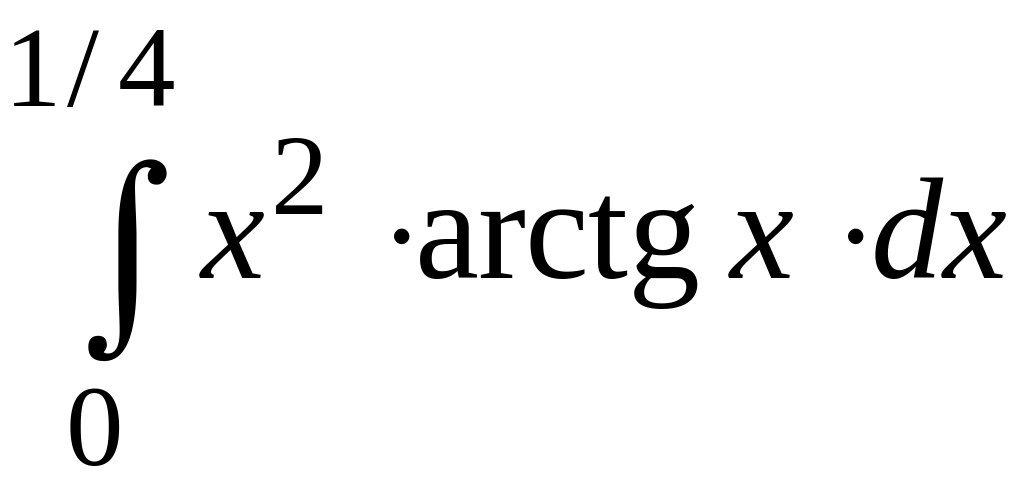
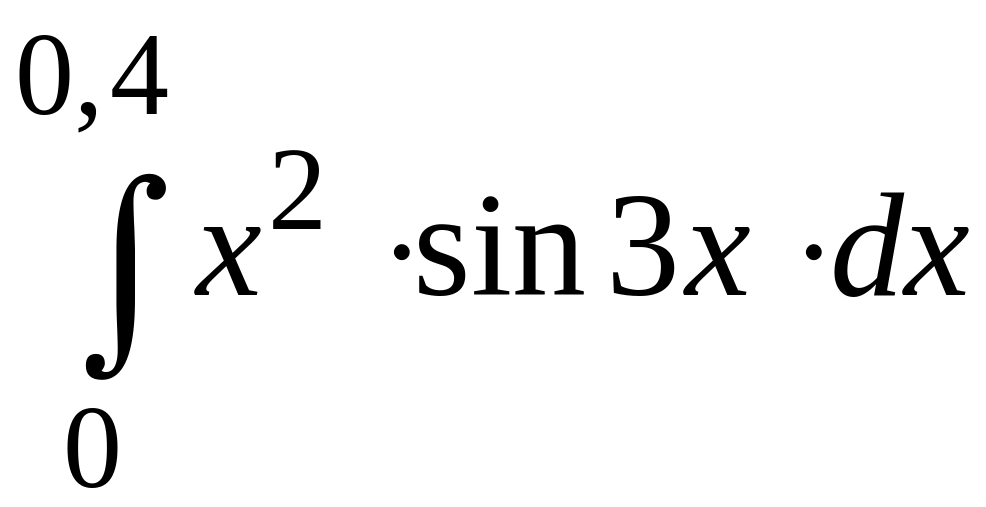
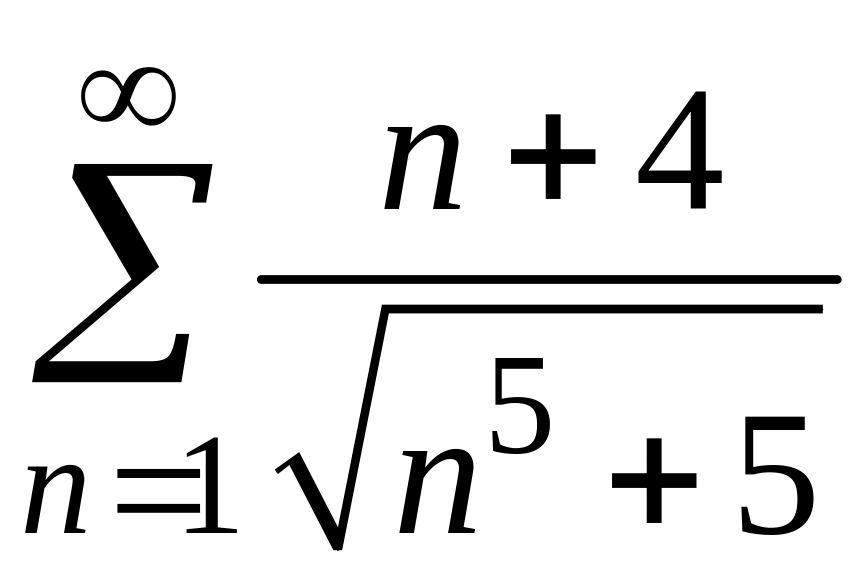
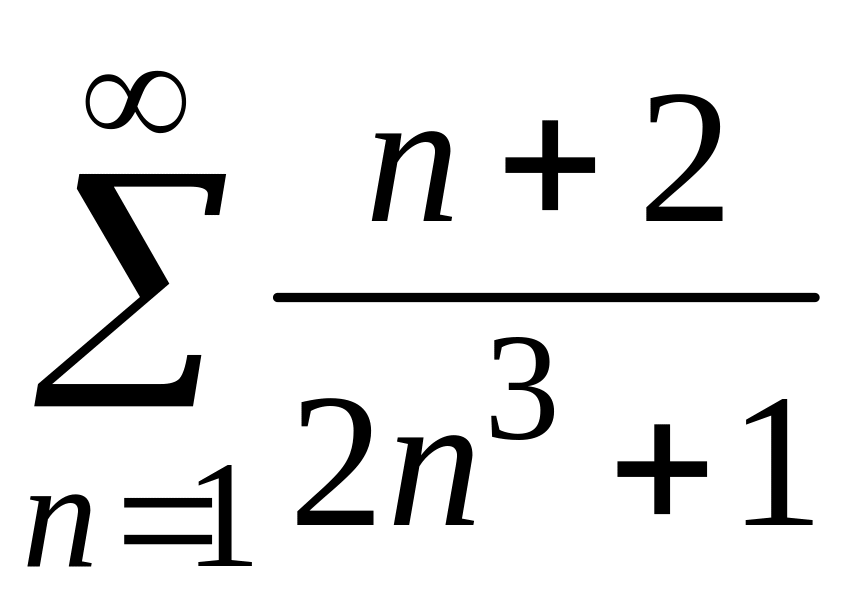
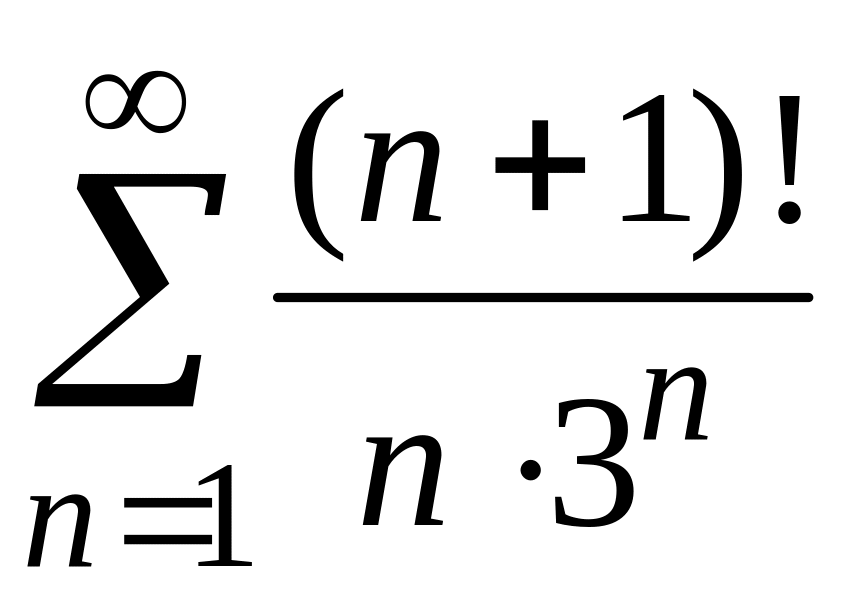
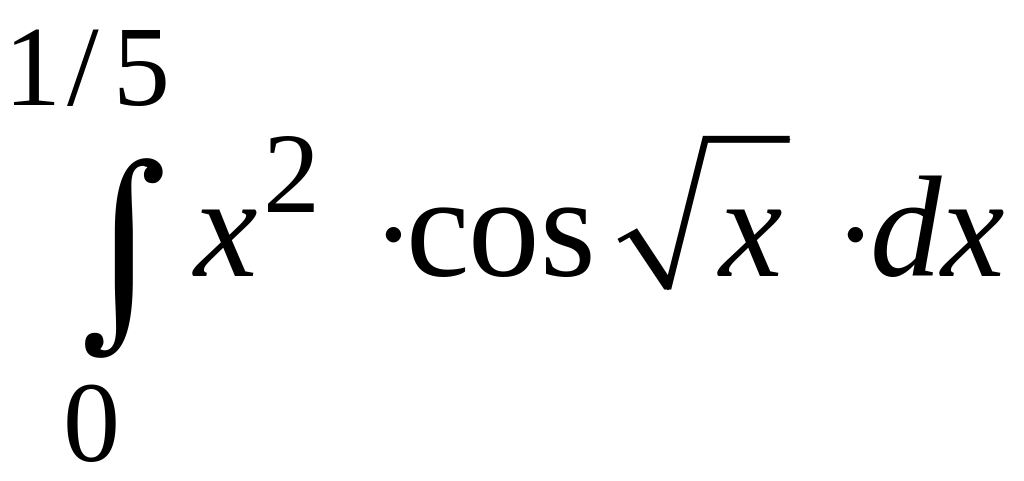
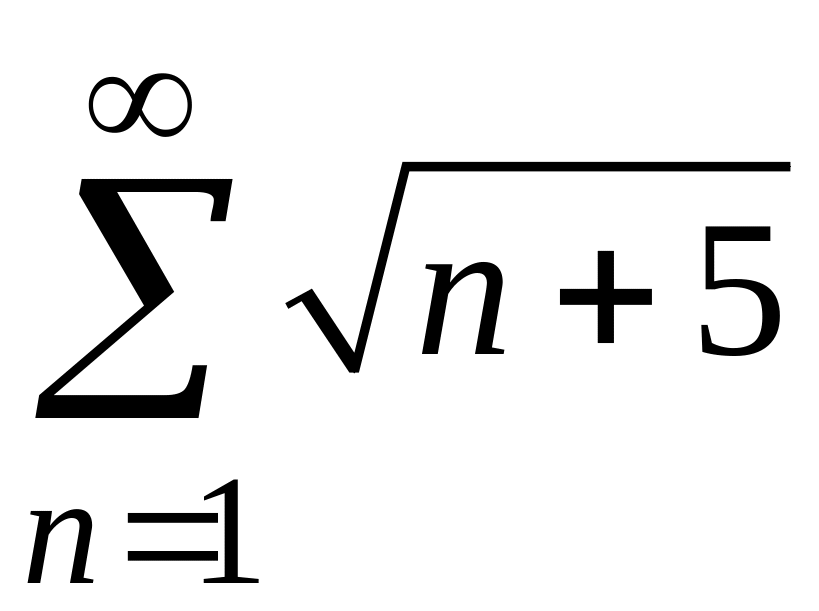
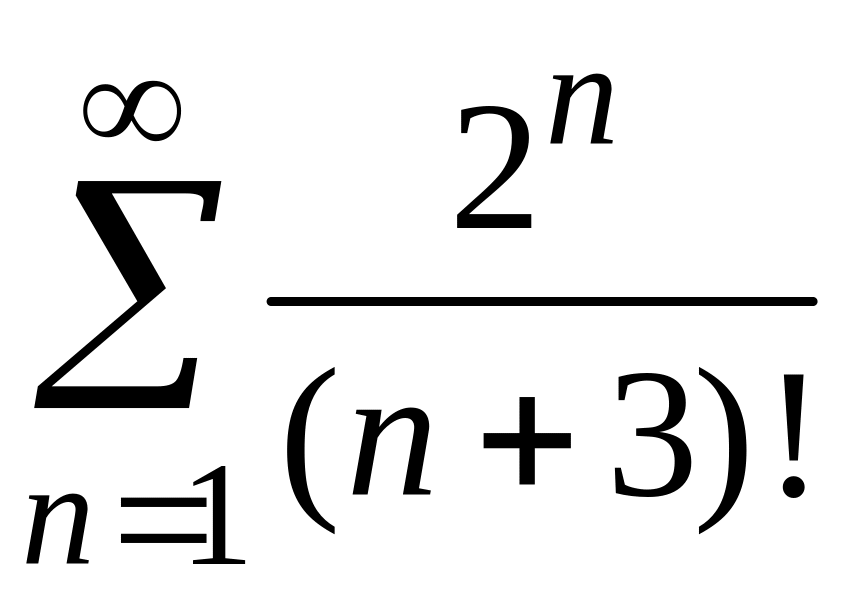
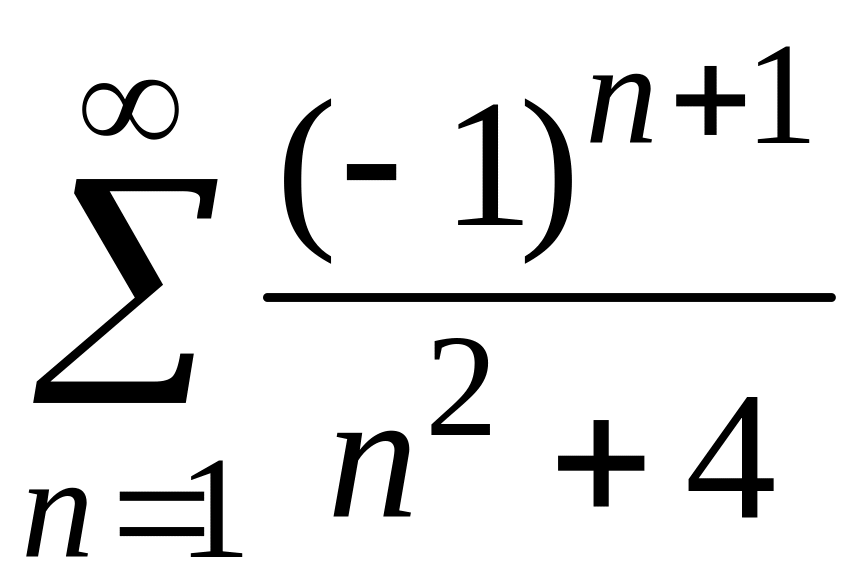
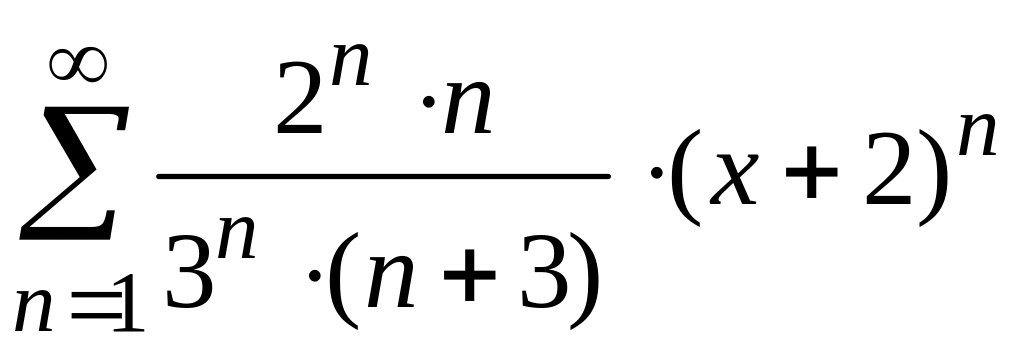
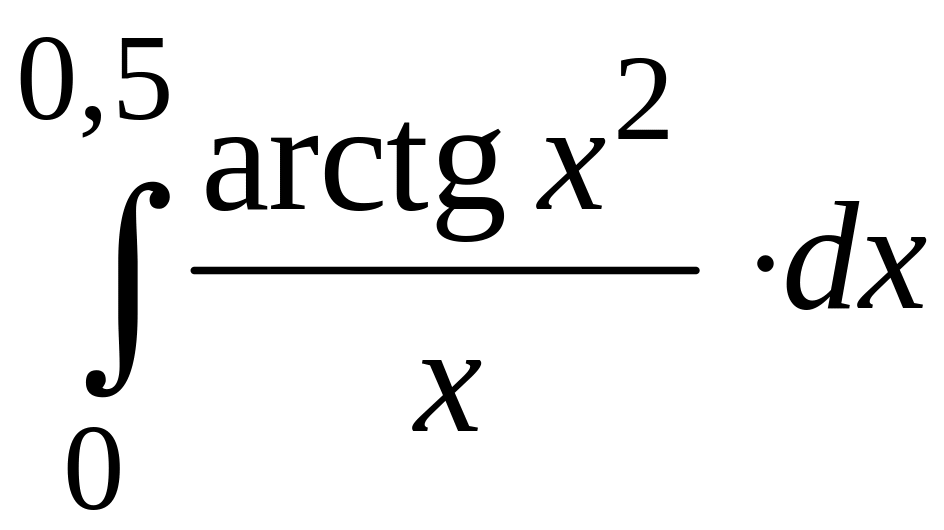
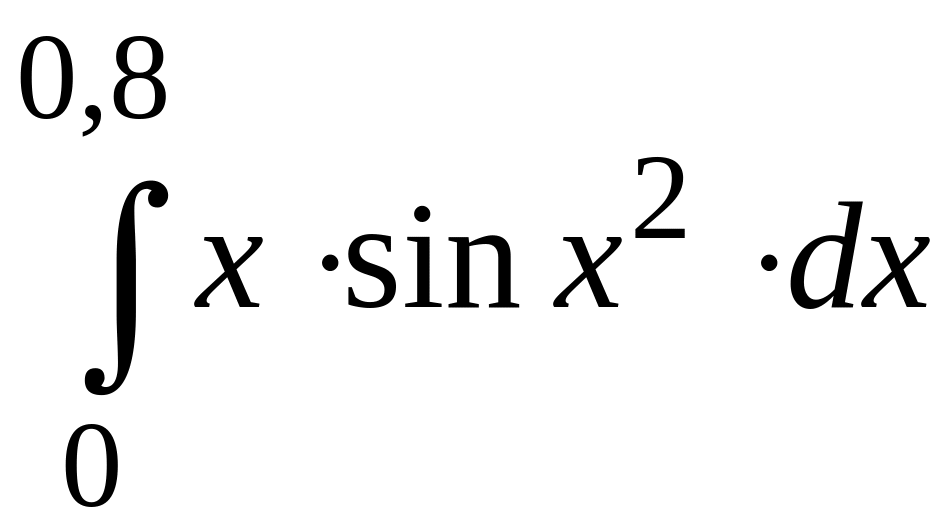
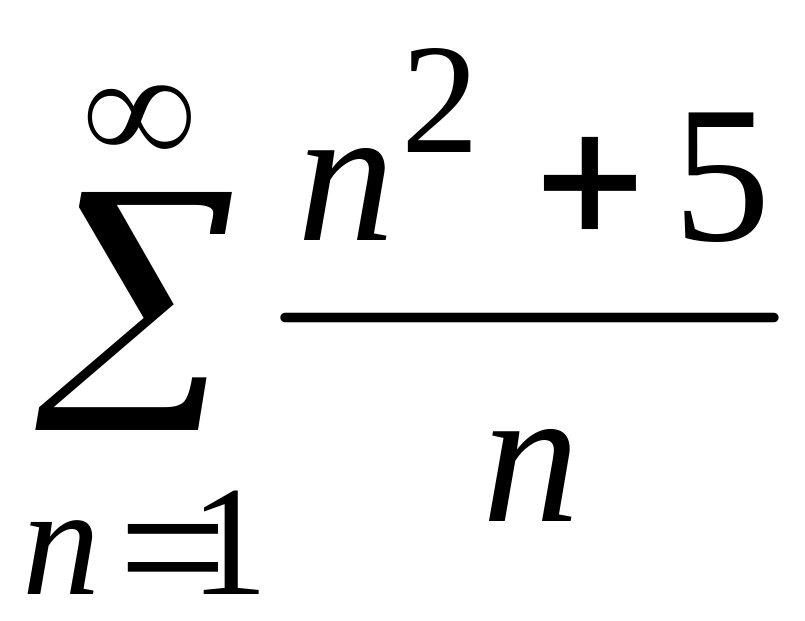
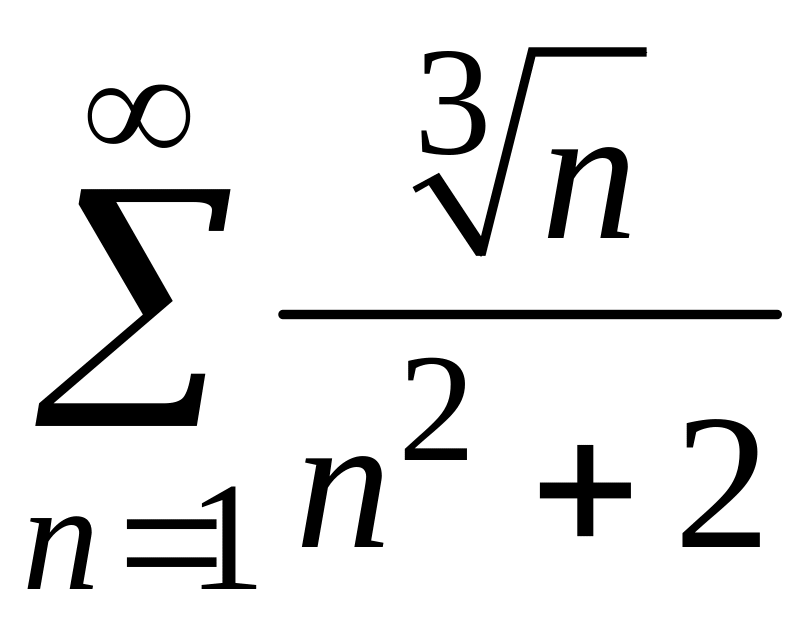
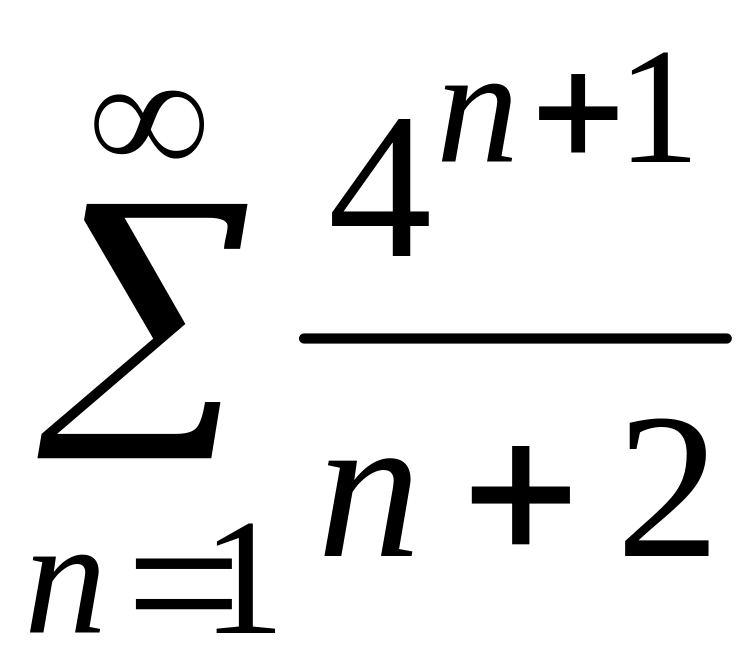
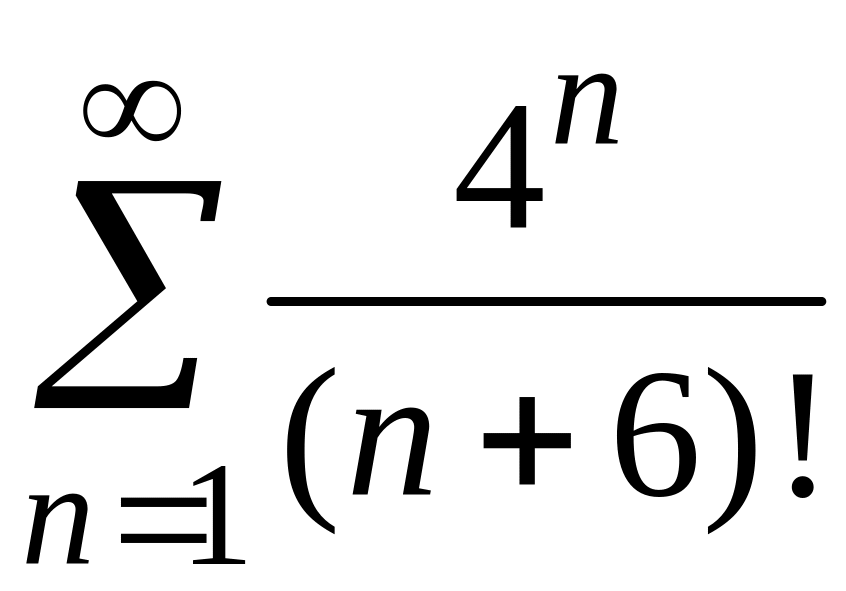
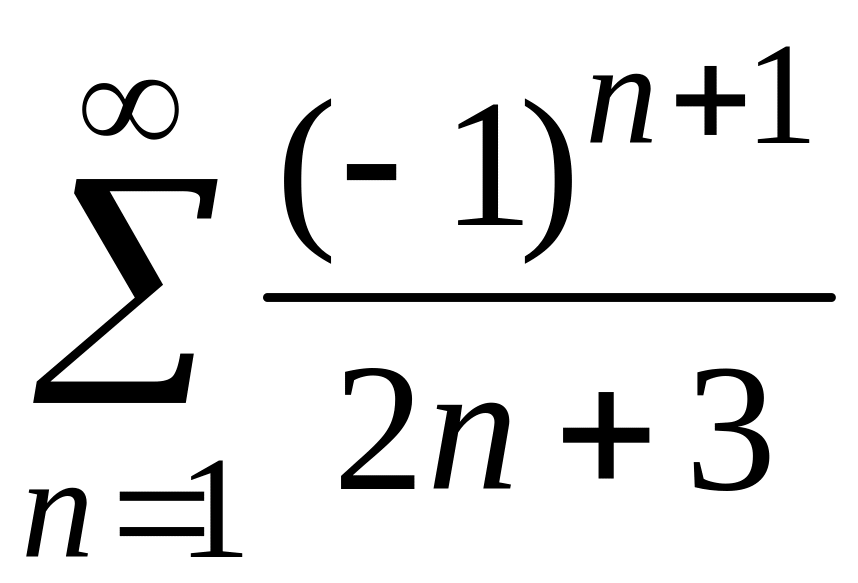
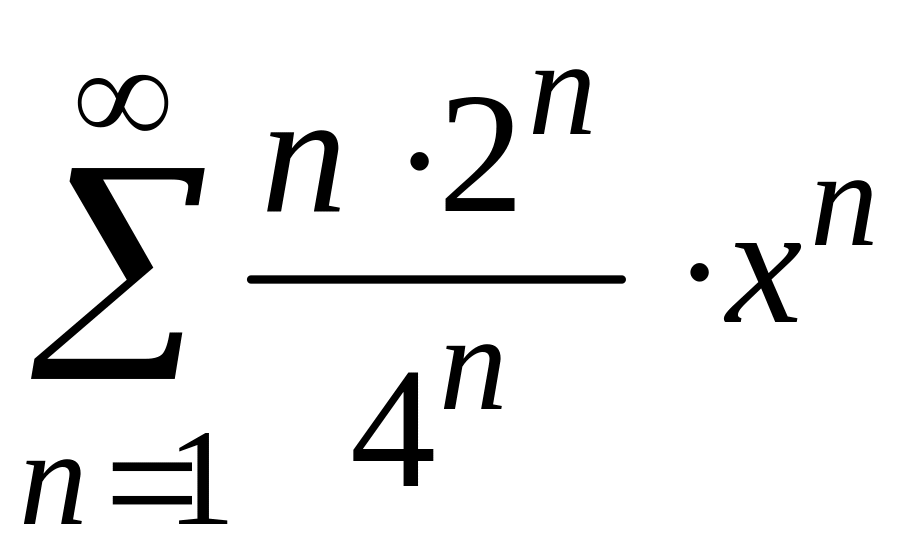
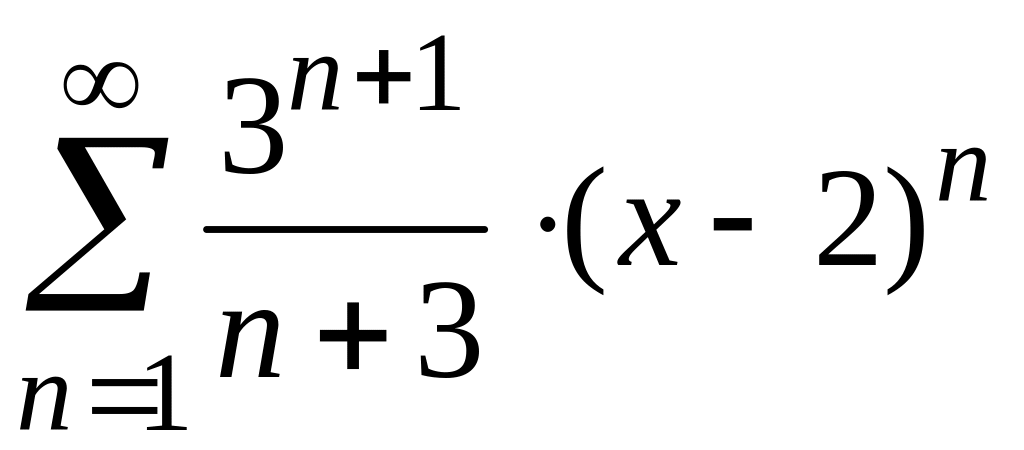
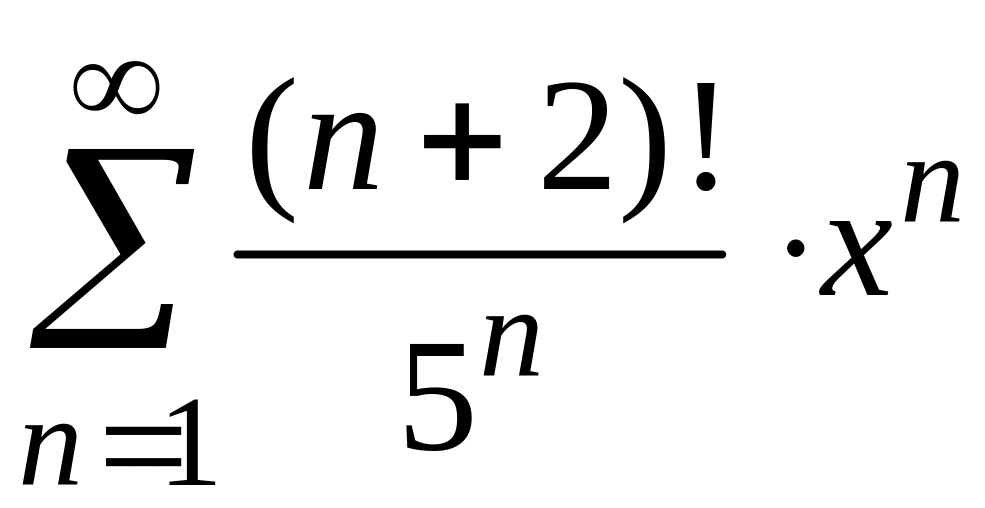
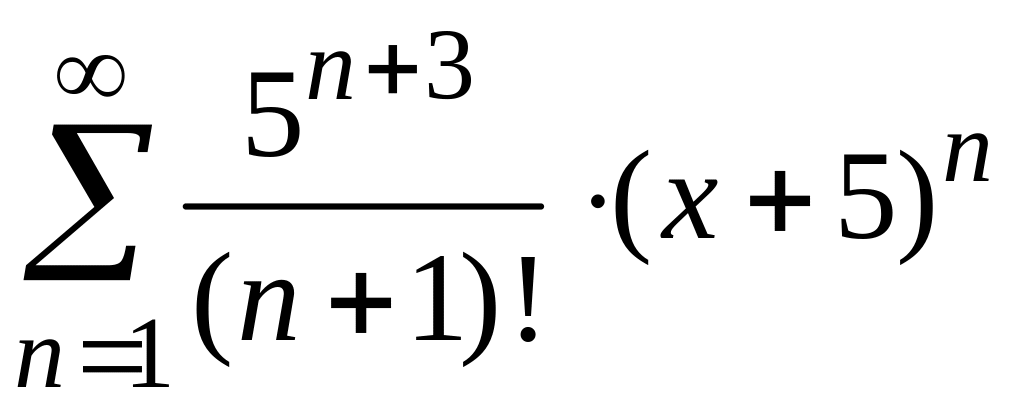
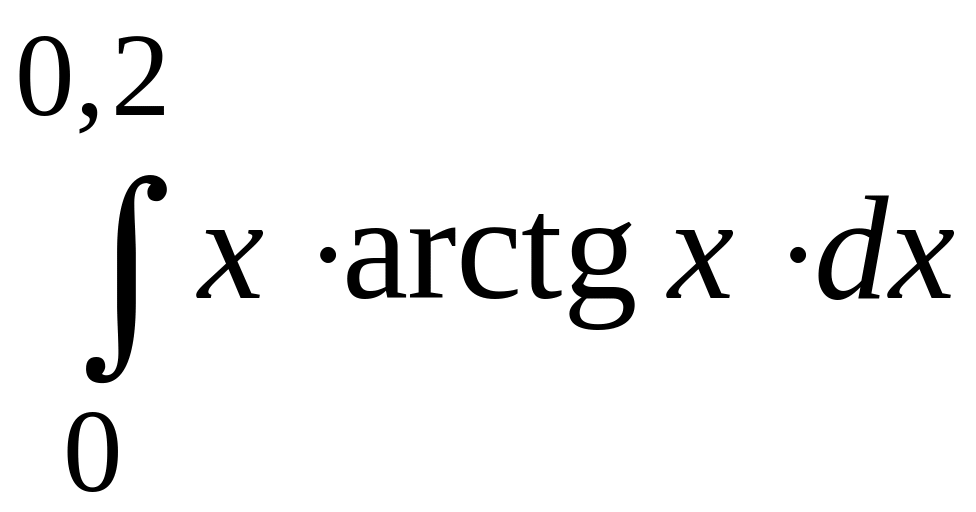
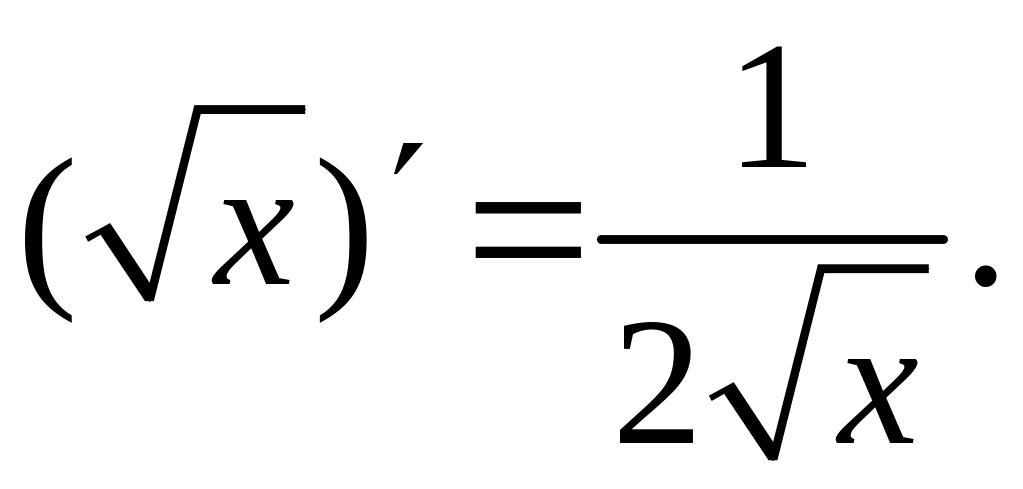
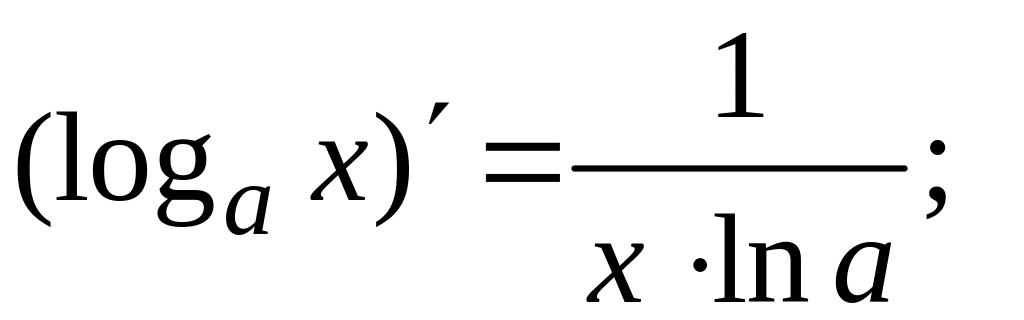
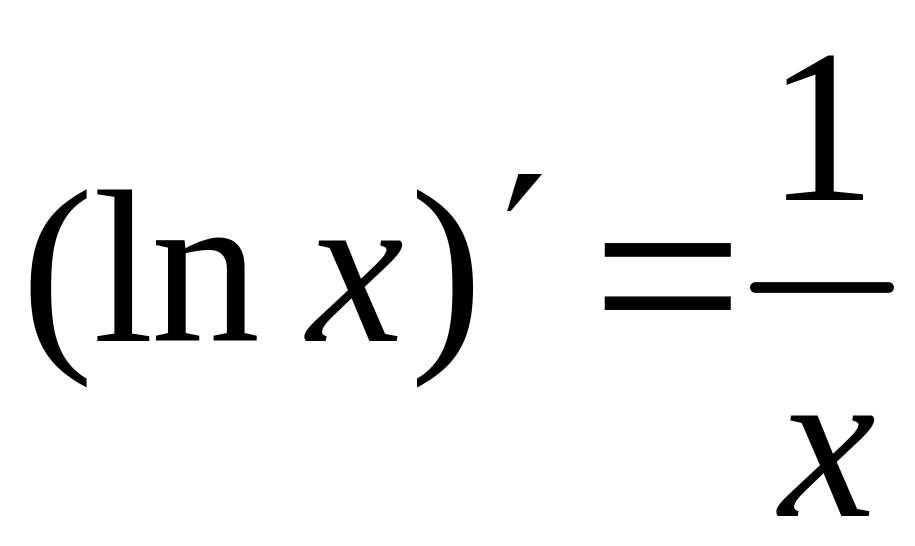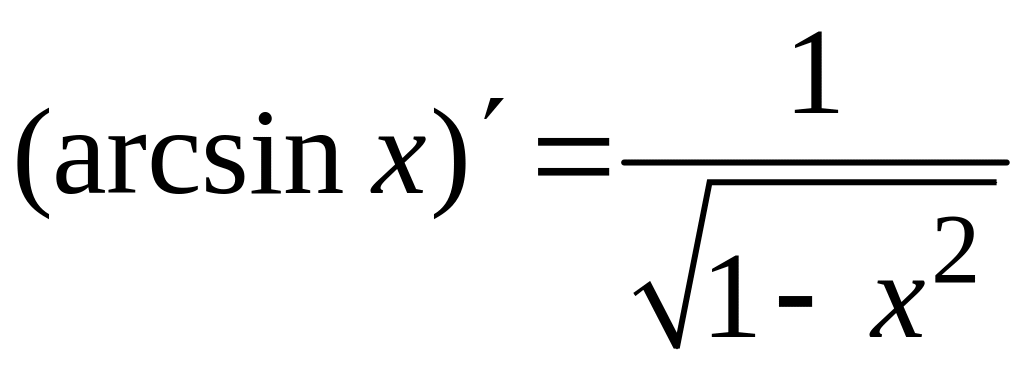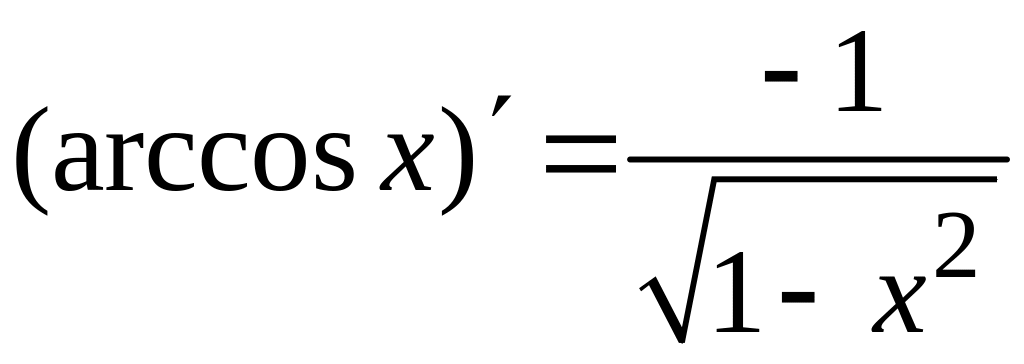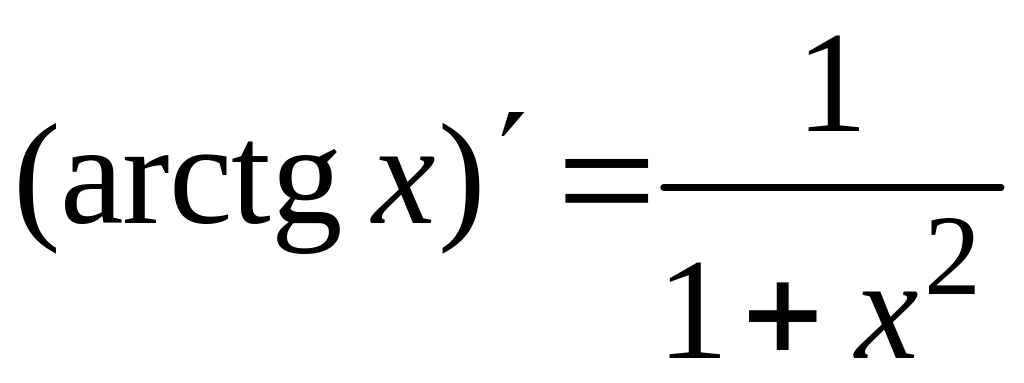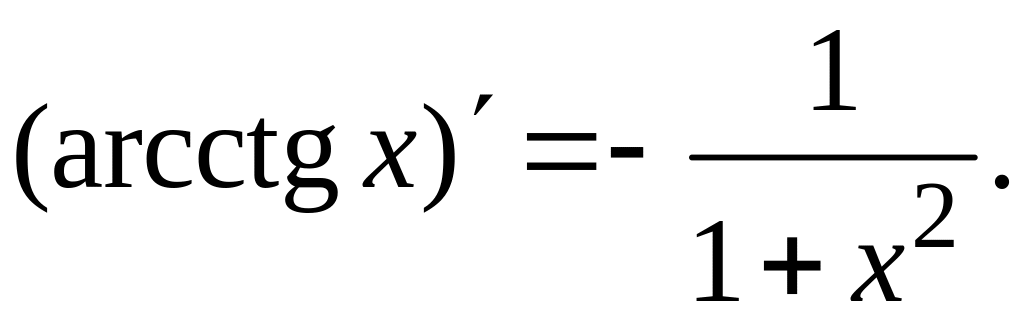
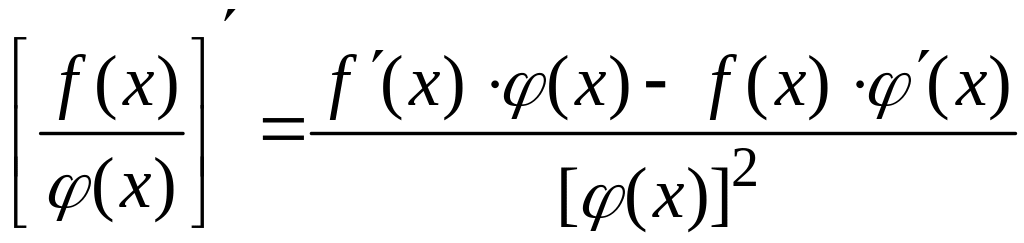где
,
то есть
,
и каждая из функций
,
дифференцируема по своему аргументу,
то
.