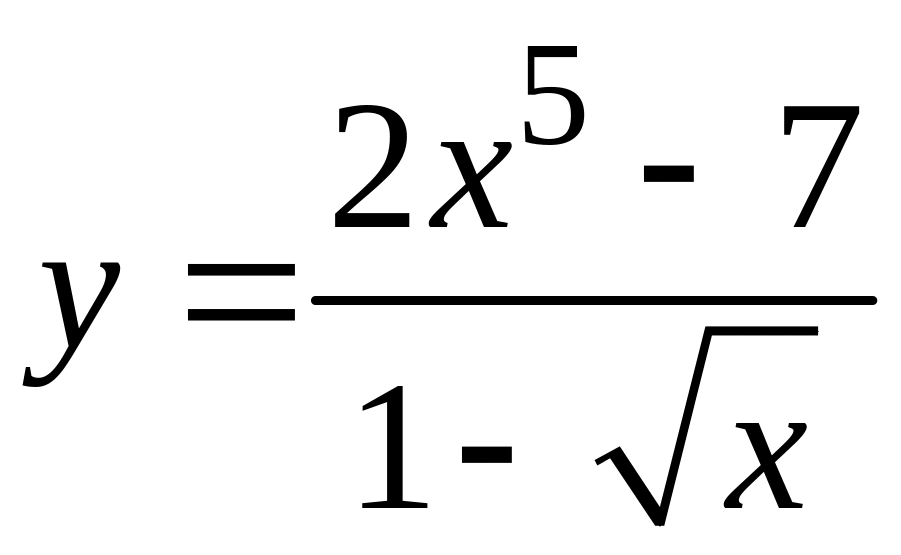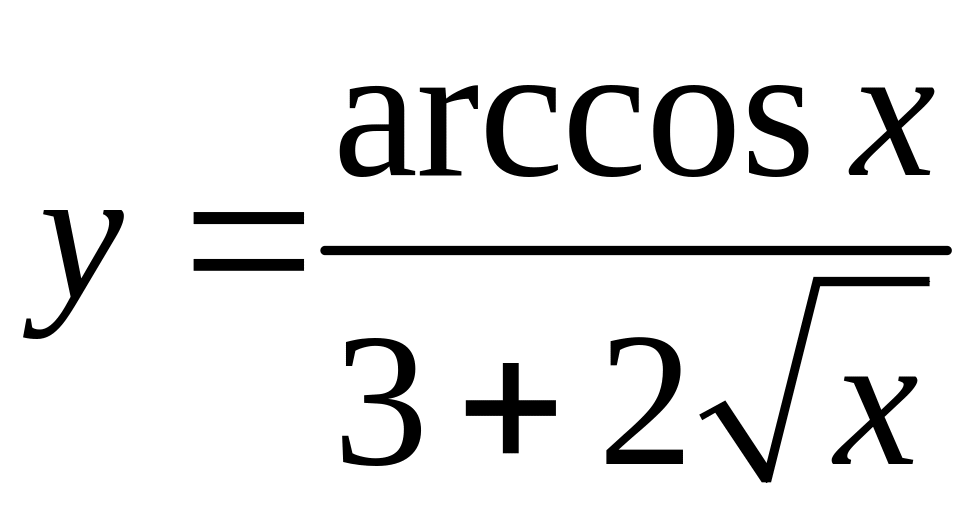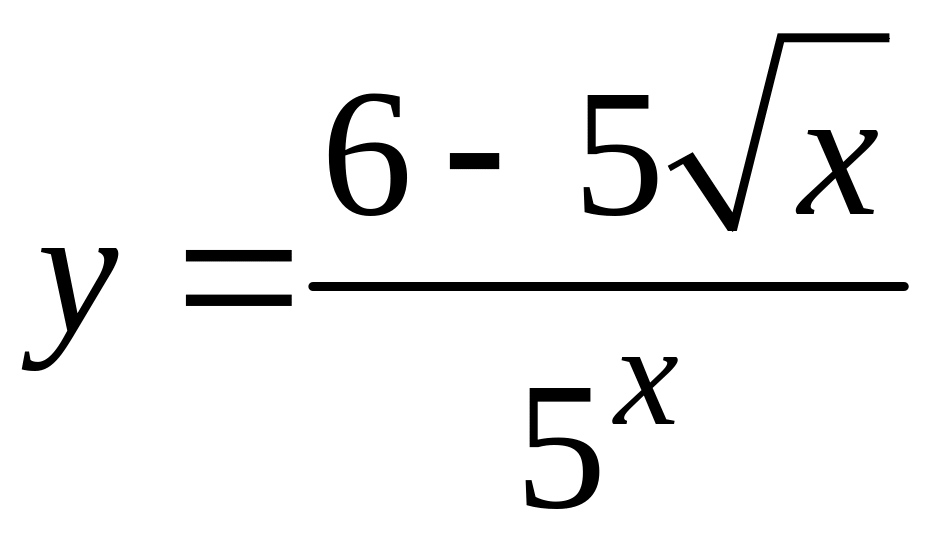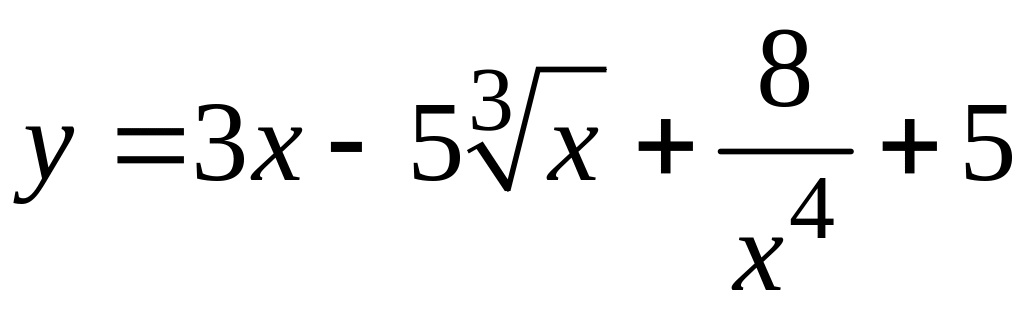m32351_3

Вариант 20.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 21.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 22.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 23.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 24.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 25.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 26.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 27.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

Вариант 28.

1.	6.
2.	7.
3.	8.
4.	9.
5.	10.

РЕШЕНИЕ ТИПОВОГО ЗАДАНИЯ

ПРИМЕР 1. Вычислить производные следующих функций:

;	;
;	.

Решение.

1. Пользуясь свойствами степеней, преобразуем выражение к виду, удобному для дифференцирования:

.

Теперь приступаем к дифференцированию функции:

2. Воспользуемся правилом дифференцирования произведения двух функций: . Тогда

.

Теперь используем простейшие правила дифференцирования и формулы дифференцирования основных элементарных функций:

3. Воспользуемся правилом дифференцирования отношения двух функций: . Тогда

.

Теперь используем простейшие правила дифференцирования и формулы дифференцирования основных элементарных функций:

.

4. Обозначим первое слагаемое заданной функции через , а второе  через . Каждое из этих слагаемых является сложной функцией. Согласно правилу дифференцирования сложной функции имеем:

1) . Обозначим . Тогда

.

2) . Обозначим . Тогда

.

Отсюда

.

ПРИМЕР 2. Провести анализ и построить графики следующих функций:

I. . II. . III. .

Решение.

I. .

1. Областью определения данной функции являются все действительные значения аргумента , то есть

.

2. Функция непрерывна на всей числовой прямой, поэтому ее график не имеет вертикальных асимптот.

Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты воспользуемся формулами

Имеем

Таким образом, у графика заданной функции наклонных асимптот нет.

3. Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

Решая полученное уравнение, делаем вывод о том, что функция имеет одну критические точки первого рода .

Разбиваем область определения этой точкой на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:

x
		0	+
y		min

.

4. Исследуем график на интервалы его выпуклости и вогнутости и точки перегиба. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

.

Из полученного результата делаем два вывода:

1. Функция не имеет критических точек второго рода, следовательно, ее график не имеет точек перегиба.

2. Так как во всех точках , то во всей области определения график функции является вогнутой линией.

5. Для построения графика в выбранной системе координат найдем точки его пересечения с осями Ох и Оу:

.

Итак, график пересекает ось Оу в точке , а ось Ох в точках . Учитывая точку минимума строим кривую (рис. 3.1).

II. .

1. Областью определения данной функции являются все действительные значения аргумента , то есть

.

2. Функция непрерывна на всей числовой прямой, поэтому ее график не имеет вертикальных асимптот.

Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты воспользуемся формулами

Имеем

Таким образом, у графика заданной функции наклонных асимптот нет.

3. Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки первого рода .

Разбиваем область определения этими точками на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:

	+		–		+
		max		min

4. Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

Итак, функция имеет одну критическую точку второго рода . Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

		0	+
		т.п.

Значение является абсциссой точки перегиба графика функции, а ордината этой точки

5. Для построения графика в системе координат изобразим точки , , соответствующие максимуму, минимуму функции, точку перегиба и точку пересечения графика с осью . С учетом результатов предыдущих исследований строим кривую (рис. 3.2).

III. .

1. Область определения

2. Исследование на непрерывность и асимптоты.

Заданная функция непрерывна всюду, кроме точки . Вычисляем односторонние пределы функции в этой точке:

;

.

Таким образом, точка является для заданной функции точкой разрыва второго рода, а прямая – вертикальной асимптотой ее графика.

Исследуем график на наличие наклонных асимптот.

;

.

Вывод: прямая – наклонная асимптота графика.

3. Исследование функции на экстремум и промежутки монотонности.

;

.

		-2	(-2; 4)	4	(4; 10)	10
	+	0	–	не сущ.	–	0	+
		max				min