
Тема 8. |
ПРИМЕРЫ РАСПРЕДЕЛЕНИЙ, ПОРОЖДЕННЫХ НОРМАЛЬНЫМ |
Основные понятия
В математической статистике важную роль играют некоторые законы распределения случайных величин, являющихся функциями независимых нормальных случайных величин. К ним относятся распределения хи-квадрат, Стьюдента и Фишера.
Распределение хи-квадрат
(![]() -распределение).
-распределение).
Пусть
![]()
![]()
независимые нормально распределенные
стандартные случайные величины:
независимые нормально распределенные
стандартные случайные величины:
![]()
Тогда распределение случайной величины
![]()
называется распределением хи-квадрат
с
![]() степенями свободы
степенями свободы
![]() .
.
Распределение Стьюдента ( распределение).
Пусть
![]()
независимые нормально распределенные
стандартные случайные величины:
независимые нормально распределенные
стандартные случайные величины:
![]() Тогда случайная величина
Тогда случайная величина

имеет по определению распределение
Стьюдента (или
![]() распределение)
с
степенями свободы
распределение)
с
степенями свободы
![]() .
.
Распределение Фишера ( -распределение).
Пусть![]()
независимые нормальные случайные
величины, причем
независимые нормальные случайные
величины, причем
![]()
Тогда по определению случайная величина

имеет распределение Фишера (или
распределение)
со степенями свободы
![]()
![]() .
.
На рис. 8.18.3 изображены графики плотностей вероятности рассматриваемых распределений.
 Рис.
8.1. Кривая распределения
Рис.
8.1. Кривая распределения
![]() при
при
n = 6 (1), n = 12 (2), n = 22 (3) и n = 32 (4).

Рис. 8.2. Кривая распределения Стьюдента при
n = 1 (1) и n = 30 (2).
 Рис.
8.3. Кривая распределения Фишера при
Рис.
8.3. Кривая распределения Фишера при
![]() (1);
(1);
![]() (2);
(2);
![]() (3).
(3).
З а м е ч а н и я.
Можно показать, что каждое из рассмотренных выше распределений при неограниченном увеличении числа степеней свободы стремится к нормальному. Это достаточно хорошо прослеживается на рис. 7.17.3.
Критические точки рассматриваемых распределений можно найти в таблицах приложений 35.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К ТЕМЕ 8
Задача 8.1. Исходя из того, что
![]()
![]()
являются
независимыми случайными величинами,
привести примеры случайных величин
![]()
Вариант |
k |
m |
p |
q |
130 |
Значения параметров назначьте сами |
|||
Примеры решения индивидуальных заданий
Пример 8.1. Заданы независимые случайные величины
![]()
![]()
![]()
Составить случайную величину, имеющую
распределение
![]() .
.
Решение. Рассмотрим случайные
величины
![]() ,
,
![]() Эти величины независимы, имеют нормальные
распределения. Найдем параметры этих
распределений:
Эти величины независимы, имеют нормальные
распределения. Найдем параметры этих
распределений:
![]()
![]()
Отсюда
![]()
![]() и, следовательно, случайная величина
и, следовательно, случайная величина
![]() ,
,
т.е. имеет распределение хи-квадрат с тремя степенями свободы.
Пример 8.2. Заданы независимые случайные величины
![]()
Составить случайную величину, имеющую
распределение
![]()
![]()
Решение. Случайные величины
![]()
![]()
![]()
имеют стандартные нормальные
распределения (![]() ).
Тогда, например, случайная величина
).
Тогда, например, случайная величина

т.е. имеет распределение Стьюдента с тремя степенями свободы.
Пример 8.3. Заданы независимые
случайные величины
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Составить случайную величину, которая
распределена по закону Фишера со
степенями свободы
![]()
Решение. Рассмотрим случайные величины
![]()
![]()
![]()
Поскольку они имеют стандартные нормальные распределения, то случайная величина
 ,
,
т.е. имеет распределение Фишера со
степенями свободы
![]()
КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ 8
Дайте определение закона распределения хи-квадрат.
Дайте определение распределения Стьюдента.
Распределение какой случайной величины называют распределением Фишера?
Как ведут себя законы распределений случайных величин
 ,
,
 при
при

Как ведет себя закон распределения случайной величины
 при
при

Заданы независимые случайные величины
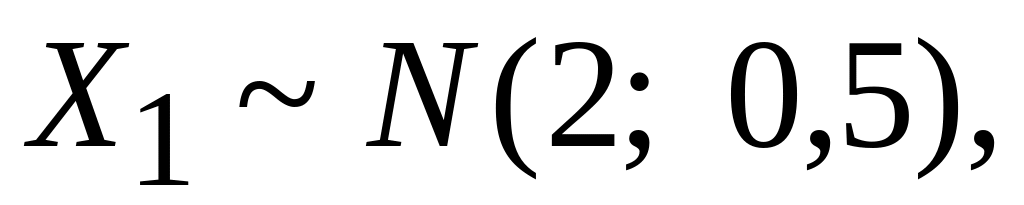
 Составить случайную величину, которая
распределена по закону хи-квадрат с
четырьмя степенями свободы.
Составить случайную величину, которая
распределена по закону хи-квадрат с
четырьмя степенями свободы.Заданы независимые случайные величины

 Составить случайную величину, имеющую
распределение Стьюдента с двумя
степенями свободы.
Составить случайную величину, имеющую
распределение Стьюдента с двумя
степенями свободы.Заданы независимые случайные величины
 Составить случайную величину, которая
распределена по закону Фишера со
степенями свободы
Составить случайную величину, которая
распределена по закону Фишера со
степенями свободы
Случайная величина X имеет распределение хи-квадрат с 4 степенями свободы. Используя таблицы критических точек распределения хи-квадрат, найти значения
 ,
если заданы вероятности событий:
,
если заданы вероятности событий:
а)
![]() где
где
![]() ;
;
б)
![]() где
где
![]()
Пусть
 независимые
случайные величины, причем
независимые
случайные величины, причем
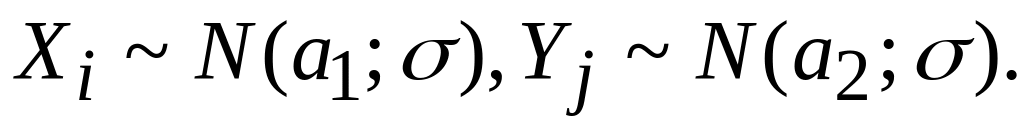 Показать, что случайная величина
Показать, что случайная величина
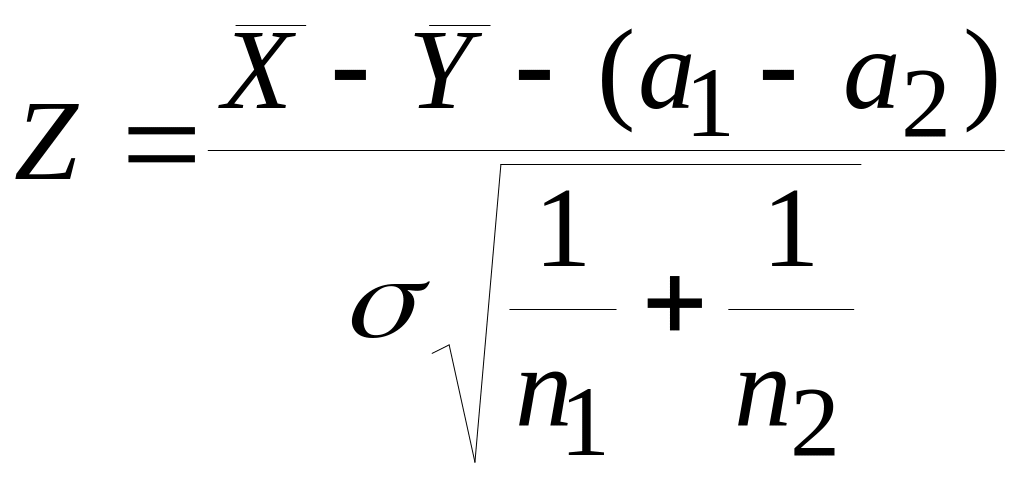 имеет распределение
имеет распределение

Случайная величина X имеет распределение Стьюдента с 10 степенями свободы. Используя таблицы критических точек распределения Стьюдента, найти значения
 если заданы вероятности событий:
если заданы вероятности событий:
а)
![]() где
где
![]()
б)
![]() где
где
![]()
в)
где
![]()
Случайная величина X имеет распределение Фишера со степенями свободы
 и
и
 Используя таблицы критических точек
распределения Фишера, найти значения
Используя таблицы критических точек
распределения Фишера, найти значения
 если заданы вероятности событий:
если заданы вероятности событий:
а)
![]() где
где
б)
![]() где
где
![]()
Тема 9. |
СИСТЕМЫ ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН: ТАБЛИЦА РАСПРЕДЕЛЕНИЯ, БЕЗУСЛОВНЫЕ И УСЛОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СОСТАВЛЯЮЩИХ, ЛИНИИ РЕГРЕССИИ, КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ. |
