m33751_3

В нашем случае , ,

.

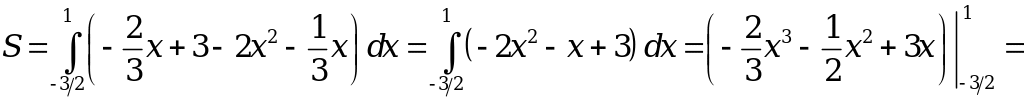
Построение всех полученных линий и характерных точек в системе координат xOy показано на рис. 2.1.

ТЕМА 3. Обыкновенные дифференциальные уравнения

Изучение этой темы следует начать со знакомства с понятиями дифференциального уравнения и его решения. Далее следует обратить внимание на различие в понятиях «решение», «общее решение» и «частное решение» дифференциального уравнения. Познакомьтесь с геометрическим смыслом этих понятий. Для того чтобы успешно решить задачи этой темы, нужно усвоить принцип деления уравнений на типы и различать методы, применяемые для решения дифференциальных уравнений.

В данном типовом задании рассмотрены следующие типы уравнений: а) дифференциальные уравнения с разделяющимися переменными; б) линейные дифференциальные уравнения первого порядка; в) линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Вопросы для самопроверки

1. Какое уравнение называется дифференциальным? Как определяется порядок уравнения?

2. Что называется общим решением дифференциального уравнения? частным решением?

3. Каков геометрический смысл общего и частного решений дифференциального уравнения первого порядка?

4. Приведите примеры дифференциальных уравнений с разделяющимися переменными.

5. Какое дифференциальное уравнение первого порядка называется линейным? Укажите способ его решения.

6. Каков вид линейного дифференциального уравнения второго порядка с постоянными коэффициентами?

7. Какую структуру имеет общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?

8. Напишите формулу общего решения линейного однородного уравнения второго порядка с постоянными коэффициентами в зависимости от корней характеристического уравнения.

9. Укажите вид частного решения линейного уравнения второго порядка с постоянными коэффициентами и правой частью вида , где – многочлен степени .

Дифференциальные уравнения с разделяющимися переменными

В общем виде дифференциальное уравнение с разделяющимися переменными записывается следующим образом

.

Для нахождения общего решения используем 4-х шаговый алгоритм.

Шаг 1. Запишем производную в виде отношения дифференциалов . В таком случае исходное уравнение примет вид

.

Шаг 2. Умножим обе части уравнения на . В результате получим

.

Шаг 3. Чтобы переменные y и x были разделены знаком равенства, разделим обе части уравнения на функцию . Имеем

.

Шаг 4. Проинтегрировав левую и правую части полученного равенства по переменным y и x, получим общий интеграл дифференциального уравнения

.

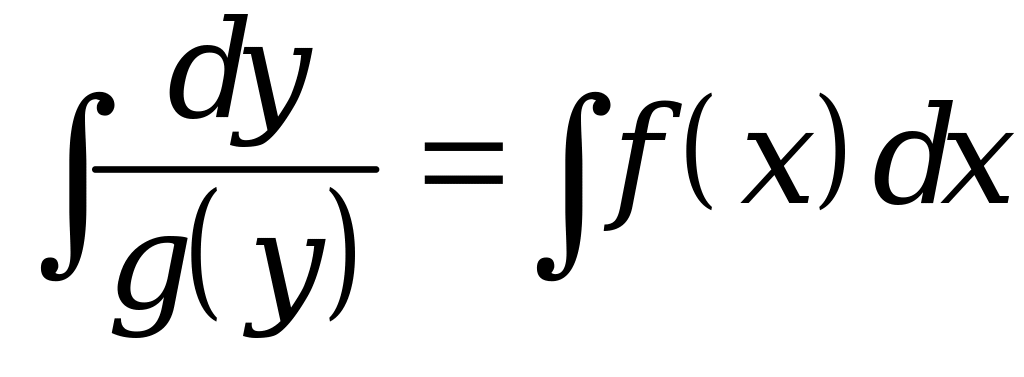Наконец, выразив y через x и C придем к общему решению дифференциального уравнения с разделяющимися переменными.

Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида

,

где , – заданные непрерывные функции от аргумента x. Решение линейного уравнения ищут в виде , где и – новые неизвестные функции. Подставляя в исходное уравнение , , будем иметь

, или

.

Поскольку искомая функция раскладывается на две неизвестные функции и , то одну из них, – функцию , всегда можно подобрать так, чтобы выражение, содержащееся в квадратной скобке, обращалось в нуль. В результате последнее уравнение преобразуется в систему двух дифференциальных уравнений

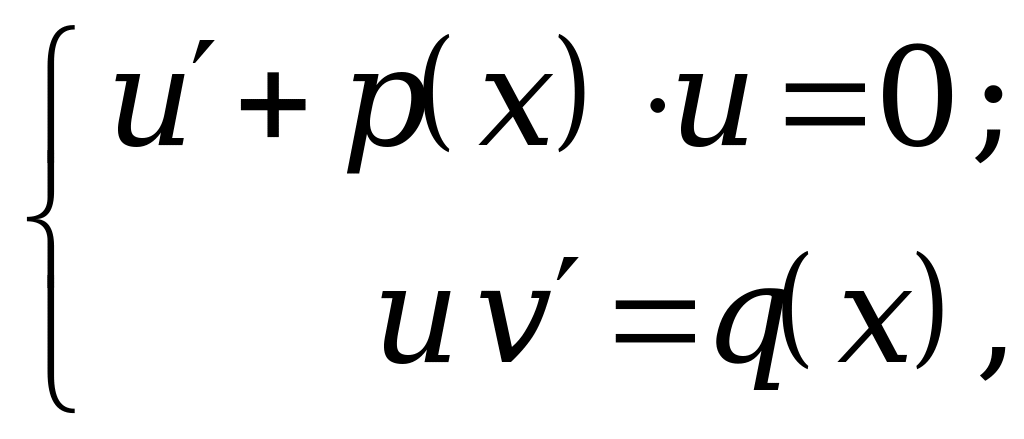
где оба уравнения являются уравнениями с разделяющимися переменными. Решая первое уравнение находим функцию . Выполняем подстановку найденной функции во второе уравнение, которое после этого принимает вид

.

Интегрирование последнего выражения позволяет определить вторую неизвестную функцию и, перемножив функции, записать общее решение линейного дифференциального уравнения первого порядка

.

Задание 4. Найти общее или частное решение указанных дифференциальных уравнений первого порядка.

Вариант 4.1	Вариант 4.2	Вариант 4.3
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.4	Вариант 4.5	Вариант 4.6
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.7	Вариант 4.8	Вариант 4.9
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.10	Вариант 4.11	Вариант 4.12
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.13	Вариант 4.14	Вариант 4.15
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.16	Вариант 4.17	Вариант 4.18
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.19	Вариант 4.20	Вариант 4.21
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.22	Вариант 4.23	Вариант 4.24
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.25	Вариант 4.26	Вариант 4.27
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Вариант 4.28	Вариант 4.29	Вариант 4.30
1. ;	1. ;	1. ;
2. , .	2. , .	2. , .

Решение типовых примеров

Пример 3.1. Найти общее решение дифференциального уравнения с разделяющимися переменными

.

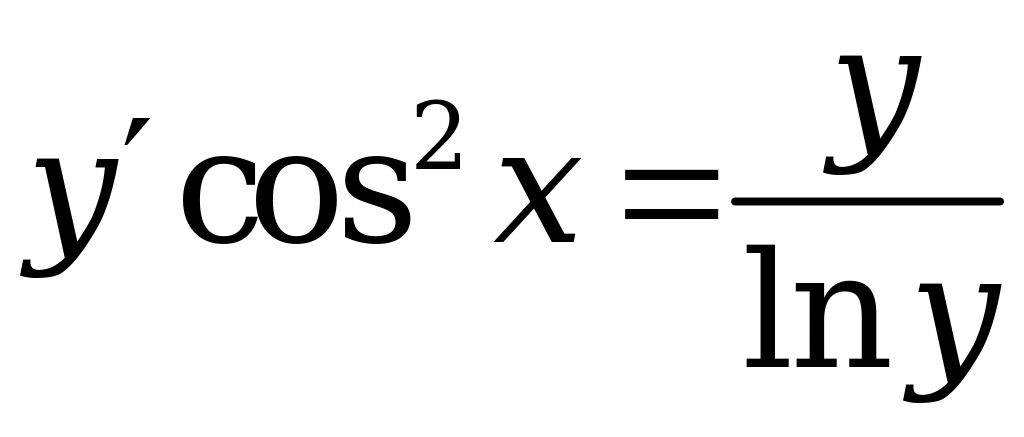Решение.

Шаг 1. Полагая , запишем данное уравнение в виде

.

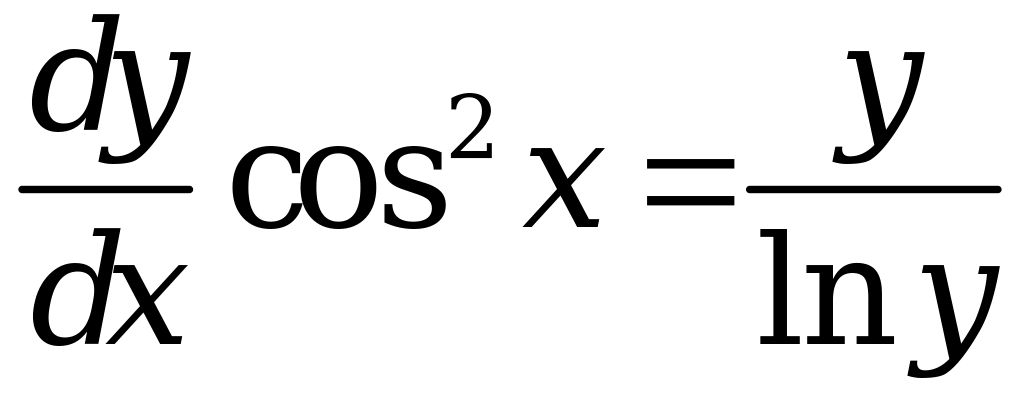Шаги 2 и 3. Произведем разделение переменных. Для этого умножим обе части уравнения на , а затем разделим на . После сокращения общих множителей получим

.

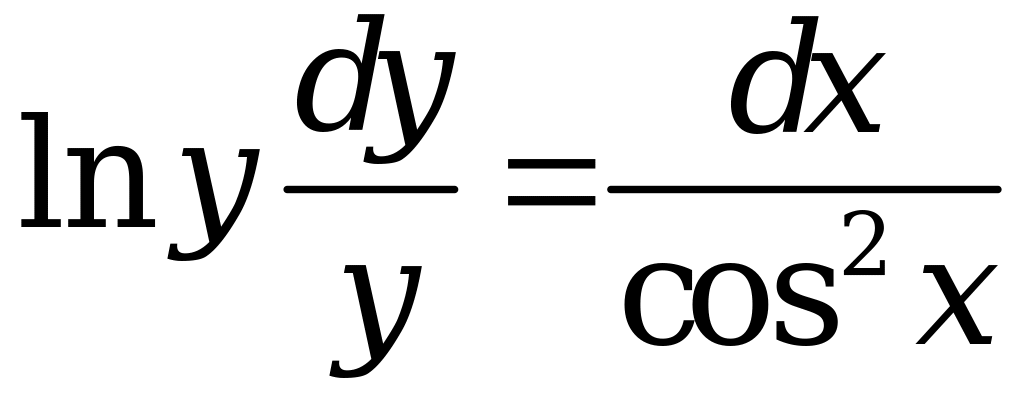Шаг 4. Проинтегрируем обе части полученного уравнения

.

Последнее выражение представляет собой общий интеграл дифференциального уравнения. Выразив y получим искомое общее решение дифференциального уравнения с разделяющимися переменными

или .

Пример 3.2. Требуется найти частное решение линейного дифференциального уравнения первого порядка , удовлетворяющее начальному условию .

Решение. Разделим обе части уравнения на x и представим искомую функцию в виде произведения двух новых неизвестных функций . В таком случае исходное дифференциальное уравнение может быть записано в виде

,

или .

Выберем функцию такой, чтобы квадратная скобка в последнем уравнении равнялась нулю. В результате от исходного уравнения мы переходим к системе из двух дифференциальных уравнений

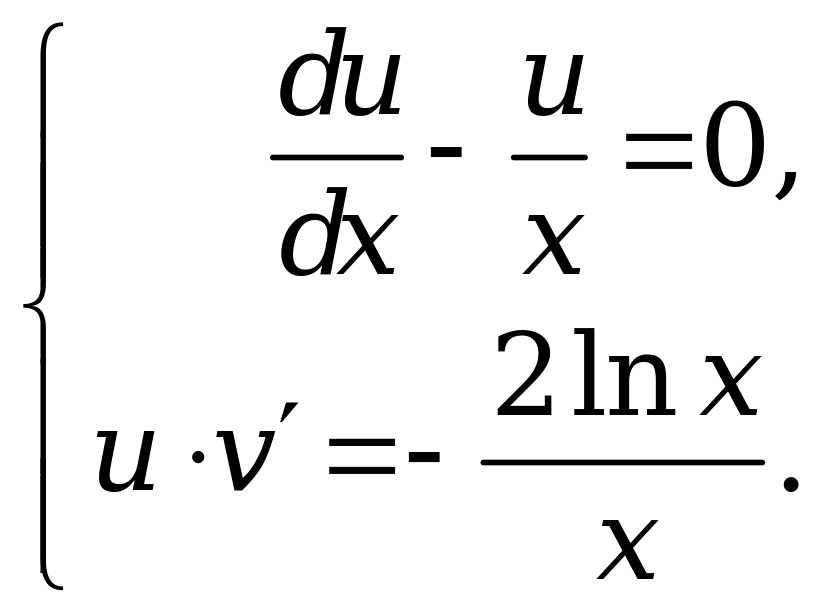(3.7)

Из первого уравнения системы (3.7) находим функцию

.

Замечание. При интегрировании последнего выражения произвольную постоянную можно положить равной нулю C  0, так как для наших целей достаточно найти лишь одно из частных решений данного уравнения.

Подставим полученное решение во второе уравнение системы (3.7). В таком случае будем иметь дифференциальное уравнение первого порядка с разделяющимися переменными

.

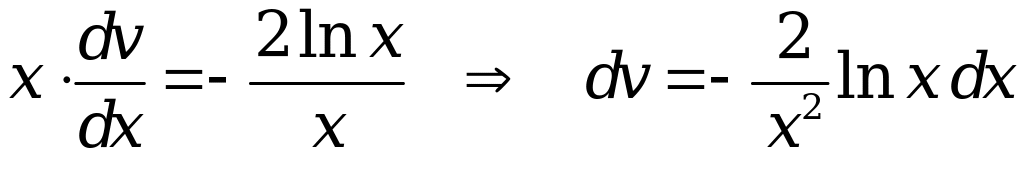Функцию определим в результате интегрирования по частям

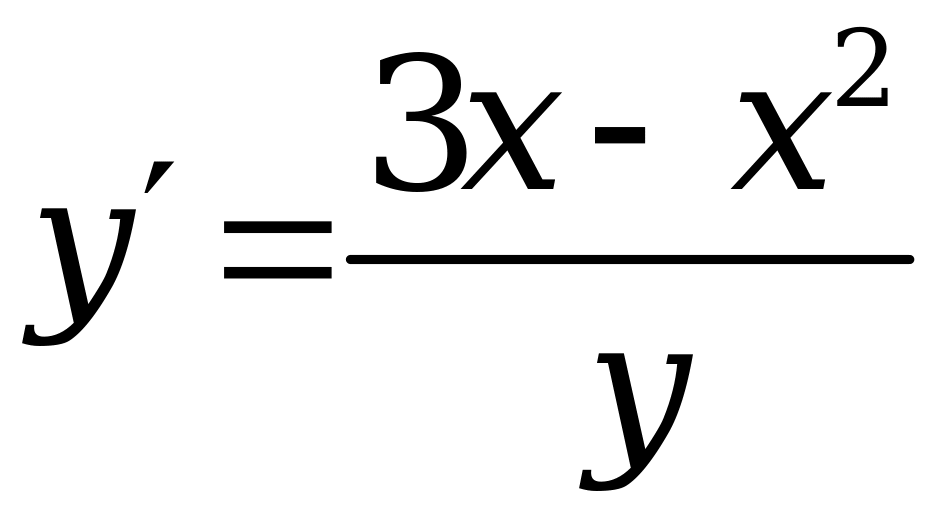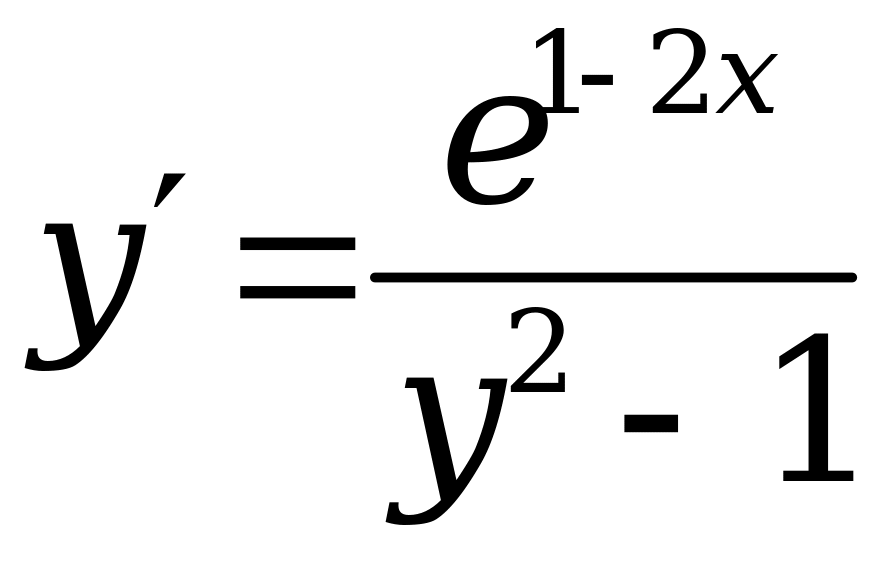26