О Б Щ И Е М Е Т О Д И Ч Е С К И Е У К А З А Н И Я

Студент выполняет тот вариант контрольных работ, номер которого (0, 1, 2,...,9) совпадает с последней цифрой его учебного шифра. Задания, обязательные для решения, также должны иметь номера, последняя цифра которых – номер варианта.

Каждая контрольная работа должна быть выполнена в отдельной ученической тетради. На внешней обложке тетради следует указать номер контрольной работы, фамилию и инициалы студента, полный учебный шифр.

Перед выполнением контрольной работы нужно изучить требуемые разделы рекомендуемой учебной литературы, конспектов лекций и практических занятий, а также разобраться в принципах решения соответствующих типовых примеров из настоящих методических указаний.

Решения всех заданий и пояснения к ним должны быть достаточно подробными и аккуратно выполненными. Для замечаний преподавателя нужно на каждой странице тетради оставлять поля.

На экзамен (зачет) студент должен явиться с зачтенными контрольными работами по соответствующим разделам учебной программы.

Если после проверки преподавателем контрольная работа помечена грифом «зачтено условно», то ее не нужно высылать на повторную проверку, а следует переделать в той же тетради указанные задания и явиться на экзамен (зачет).

Если контрольная работа не зачтена, то необходимо внести в ее содержание исправления и дополнения, указанные рецензентом, и выслать работу на повторную проверку.

Рекомендуемая литература

1. Ефимов Н.В. Краткий курс аналитической геометрии. -М.: Наука, 1972.

2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. –М.: Наука, 1975.

3. Гмурман В.Е. Теория вероятностей и математическая статистика.-М.: Высш. школа, 1999.

4. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. Ч. I, II.-М.: Высш. школа, 1974.

Тема 1. Решение систем линейных алгебраических уравнений

В ЗАДАЧАХ 1 - 10 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.

1.	2.	3.
4.	5.	6.
7.	8.	9.

10.

РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть требуется, используя формулы Крамера, решить систему

Решение. Подсчитаем сначала главный определитель системы , воспользовавшись следующим правилом вычисления определителей третьего порядка:

.

У нас

Так как , делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители :

Далее, воспользовавшись формулами Крамера, окончательно получим

Осуществим проверку правильности полученного решения, подставив его в левую часть каждого уравнения заданной системы:

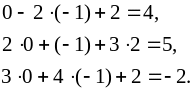
Все три равенства верные, поэтому делаем вывод о правильности полученного решения

Тема 2. Аналитическая геометрия на плоскости

В ЗАДАЧАХ 11 - 20 даны координаты вершин треугольника .

Найти: 1) длину стороны ; 2) уравнения сторон и , их угловые коэффициенты; 3) внутренний угол при вершине в радианах с точностью до 0,01; 4) уравнение медианы ; 5) уравнение и длину высоты ; 6) уравнение прямой, проходящей через точку параллельно прямой и точку ее пересечения с высотой .

Треугольник и все полученные линии построить в системе координат .

11.	(2; 2),	(5; 6),	(6; 4).
12.	(4; –2),	(7; 2),	(8; 0).
13.	(0; 2),	(3; 6),	(4; 4).
14.	(4; 1),	(7; 5),	(8; 3).
15.	(3; 2),	(6; 6),	(7; 4).
16.	(–2; 1),	(1; 5),	(2; 3).
17.	(4; –3),	(7; 1),	(8; –1).
18.	(–2; 2),	(1; 6),	(2; 4).
19.	(5; 0),	(8; 4),	(9; 2).
20.	(2; 3),	(5; 7),	(6; 5).

РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть

1. Расстояние между точками и определяется по формуле

(1)

воспользовавшись которой находим длину стороны :

2. Уравнение прямой, проходящей через две заданные точки плоскости и , имеет вид

(2)

Подставляя в (2) координаты точек и , получаем уравнение стороны :

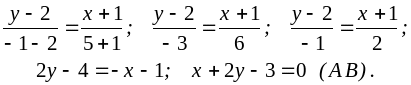
Угловой коэффициент прямой найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом .

У нас , то есть откуда .

Аналогично получим уравнение прямой и найдем ее угловой коэффициент:

Далее

3. Для нахождения внутреннего угла нашего треугольника воспользуемся формулой:

(3)

Отметим, что порядок вычисления разности угловых коэффициентов, стоящих в числителе этой дроби, зависит от взаимного расположения прямых и . Подумайте, как бы Вы стали искать внутренние углы и треугольника ?

Подставив ранее вычисленные значения и в (3), находим:

Теперь, воспользовавшись таблицами В.М. Брадиса или инженерным калькулятором, получаем .

4. Для составления уравнения медианы найдем сначала координаты точки , которая лежит на середине отрезка :

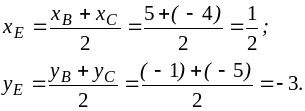
Подставив в уравнение (2) координаты точек и , получаем уравнение медианы:

5. Для составления уравнения высоты воспользуемся уравнением прямой, проходящей через заданную точку с заданным угловым коэффициентом , которое имеет вид

(4)

и условием перпендикулярности прямых и , которое выражается соотношением , откуда Подставив в (4) вместо значение , а вместо соответствующие координаты точки , получим уравнение высоты :

Для вычисления длины высоты воспользуемся формулой отыскания расстояния от заданной точки до заданной прямой с уравнением , которая имеет вид

(5)

Подставив в (5) вместо координаты точки , а вместо коэффициенты уравнения прямой , получаем

6. Так как искомая прямая параллельна прямой , то

. Подставив в уравнение (4) вместо координаты точки , а вместо значение , получаем уравнение прямой :

Для отыскания координат точки решаем совместно уравнения прямых и :

Таким образом,

Треугольник , высота , медиана , прямая и точка построены в системе координат на рис. 1.

y

2

0

x

-4 -1 5

-5

Рис. 1