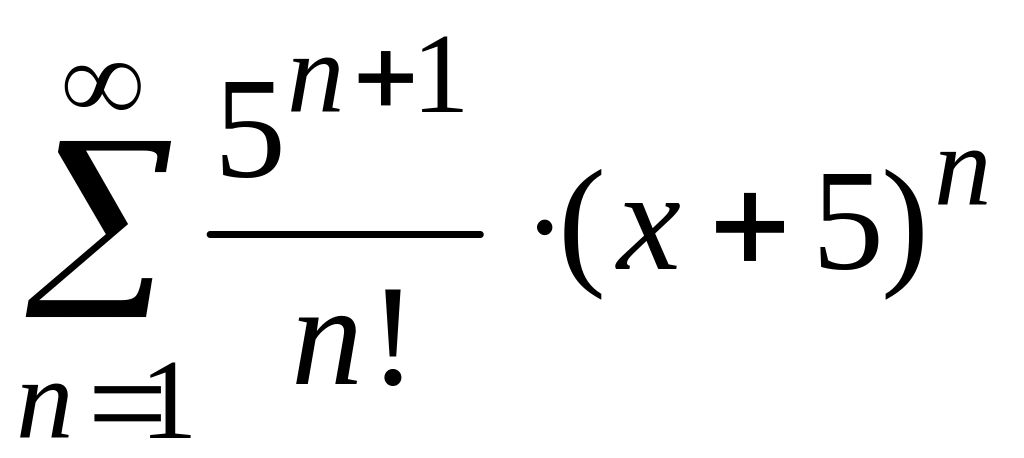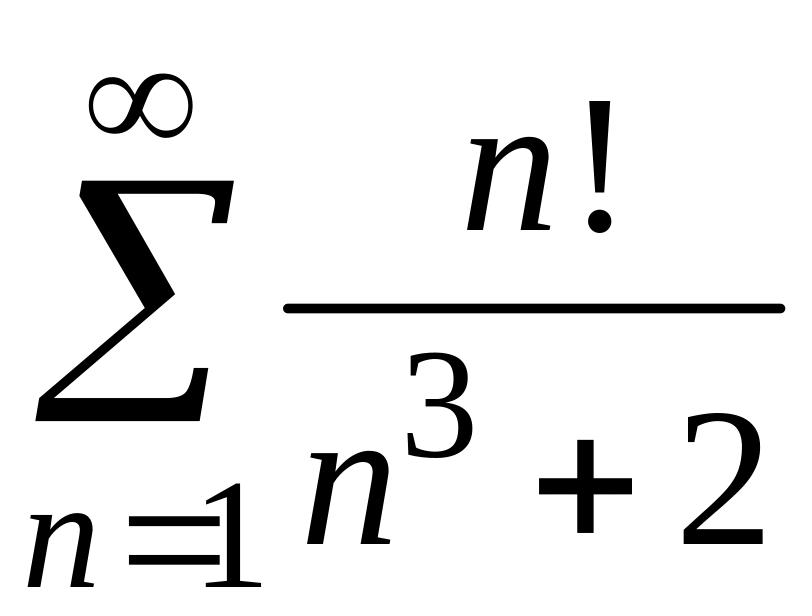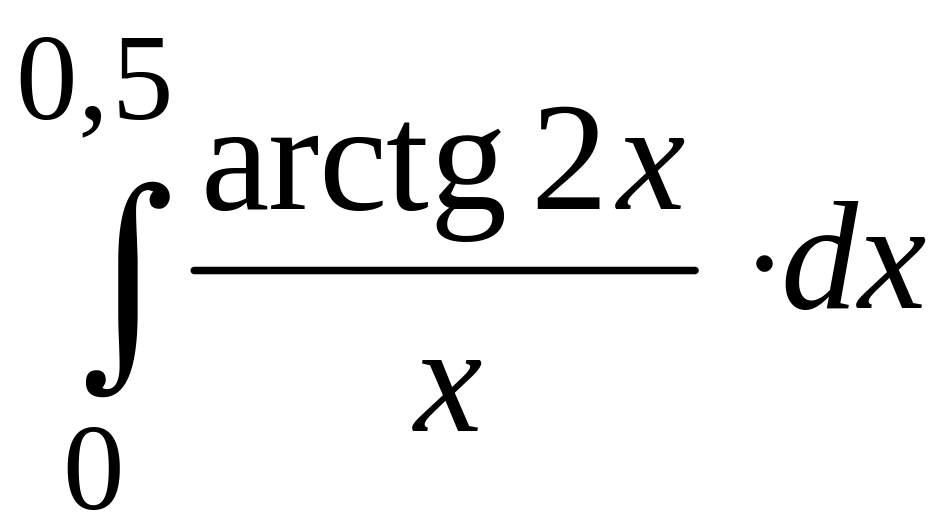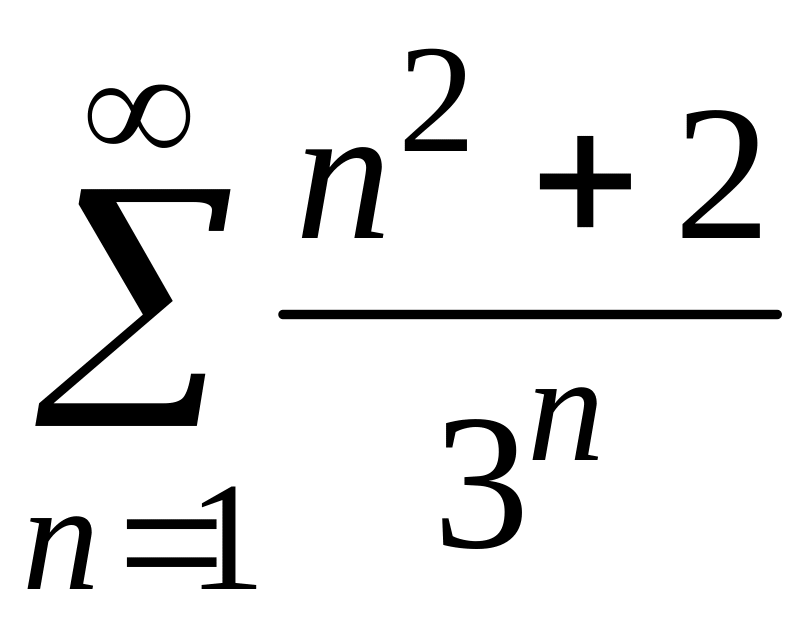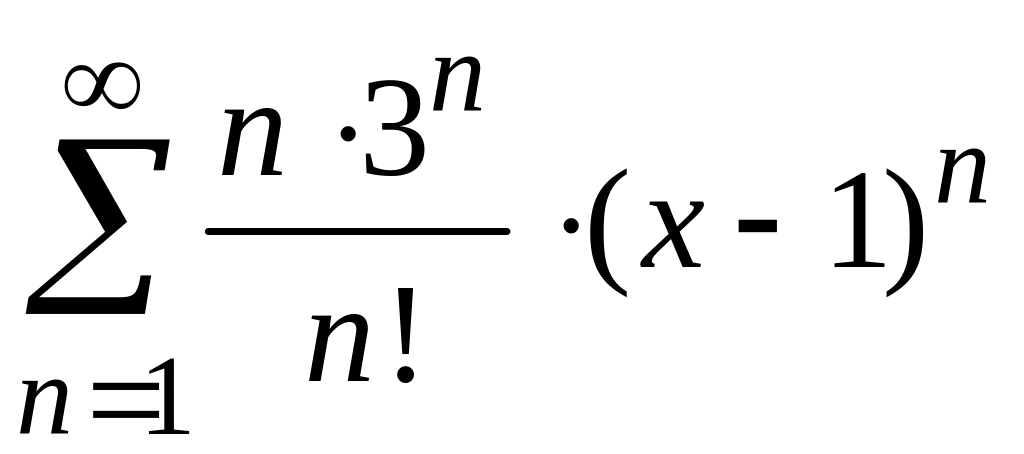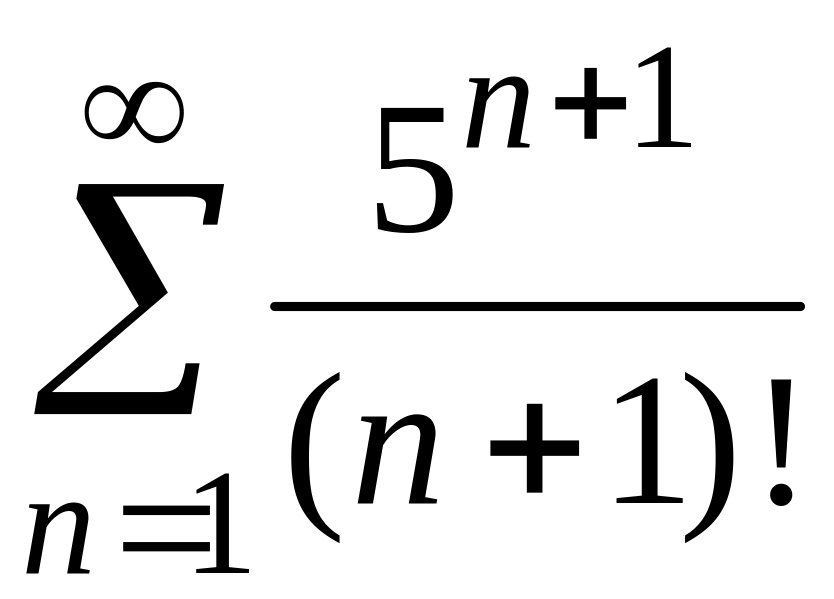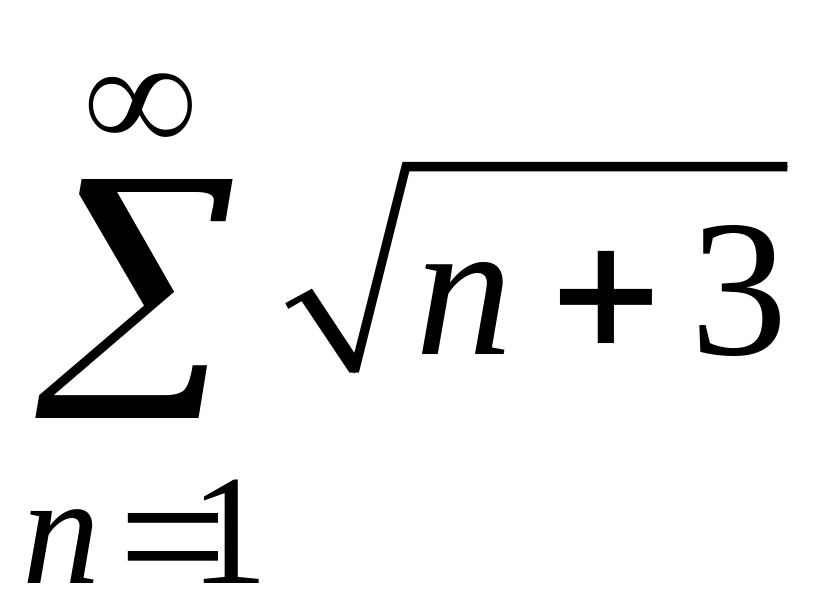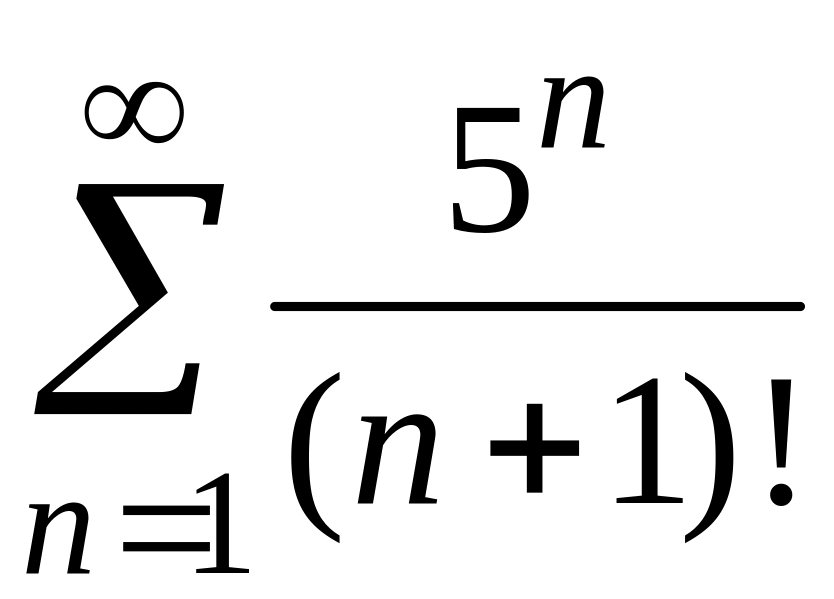m32352_12
.DOC
из
корней характеристического уравнения
с выражением
![]() ,
то подбираем частное решение исходного
неоднородного уравнения по формуле
,
то подбираем частное решение исходного
неоднородного уравнения по формуле
![]()
где А, В неопределенные коэффициенты. Для отыскания их значений находим
![]()
![]() .
.
Подставляя
![]() и
и
![]() в неоднородное уравнение и приводя
подобные члены, получаем
в неоднородное уравнение и приводя
подобные члены, получаем
![]()
откуда
![]()

 .
.
Следовательно,
 .
.
Итак, общее решение данного уравнения имеет вид
 .
.
ТЕМА VI. Ряды
ВОПРОСЫ К ТЕМЕ
Числовой ряд. Частичные суммы. Сходимость. Необходимый признак сходимости.
Исследование поведения бесконечной геометрической прогрессии. Обобщенный гармонический ряд и условие его сходимости.
Достаточные признаки сходимости числовых знакопостоянных рядов (признаки сравнения, Даламбера).
Знакочередующиеся числовые ряды. Понятие абсолютной сходимости, ее связь со сходимостью в обычном смысле. Признак Лейбница. Следствие из теоремы Лейбница.
Степенные ряды. Радиус, интервал, область сходимости.
Ряды Тейлора и Маклорена.
Примеры разложения функций в степенной ряд.
Приложения степенных рядов к приближенному вычислению определенных интегралов и приближенному решению задачи Коши для обыкновенных дифференциальных уравнений.
ТИПОВОЙ РАСЧЕТ 6
ЗАДАЧА 6.1.
Исследовать на сходимость числовые ряды.
Найти радиусы и интервалы сходимости степенных рядов.
Заданные интегралы вычислить приближенно с точностью до 0,01.
Найти три первые отличные от нуля члена разложения в степенной ряд решения задачи Коши.
Вариант 1.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 2.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 3.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 4.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6. |
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 5.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8. |
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 6.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 7.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 8.
I. |
1.
|
2.
|
3.
|
4. |
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 9.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||
Вариант 10.
I. |
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7. |
8.
|
|
II. |
1.
|
2.
|
||
3.
|
4.
|
|||
III. |
1.
|
2.
|
||
IV. |
1.
|
2.
|
||