m32352_5
.DOC
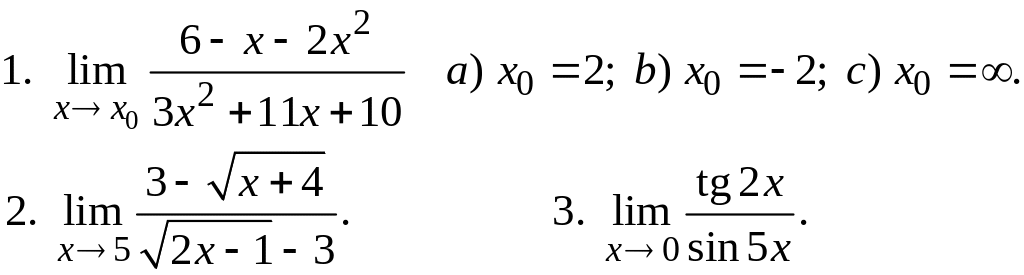
II. Используя первое определение непрерывности, доказать непрерывность функций в их областях определения:

III. Классифицировать точки разрыва заданных функций, найти вертикальные и горизонтальные асимптоты их графиков и отразить на чертеже гипотезы поведения графиков:

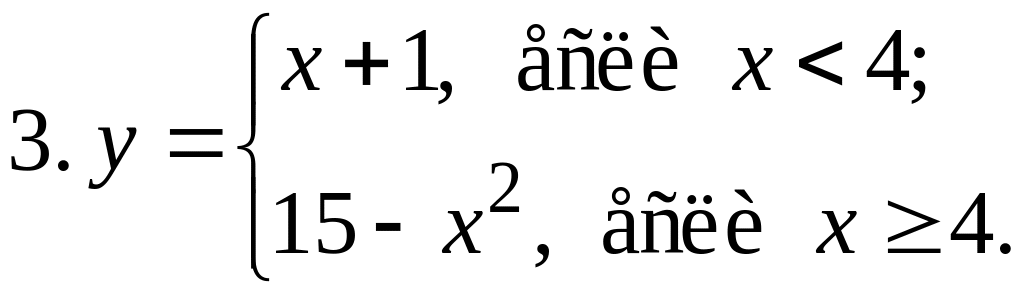
Решение.
I.
1а)

1b)

Для освобождения от имеющейся неопределенности представим числитель и знаменатель дроби в виде произведения простейших сомножителей:

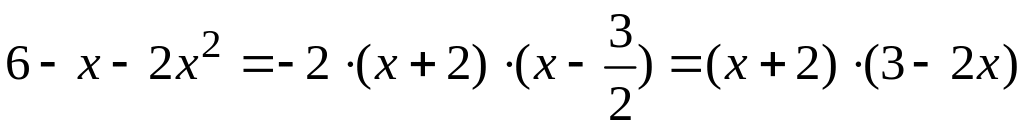 ;
;

 .
.
Возвращаемся к вычислению предела и получаем
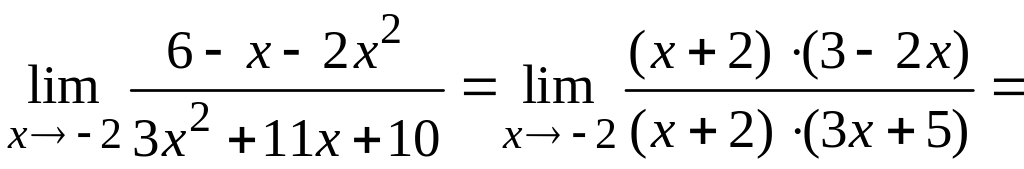
 .
.
1c)

Чтобы
устранить эту неопределенность, разделим
числитель и знаменатель дроби на
![]() .
Тогда получим
.
Тогда получим
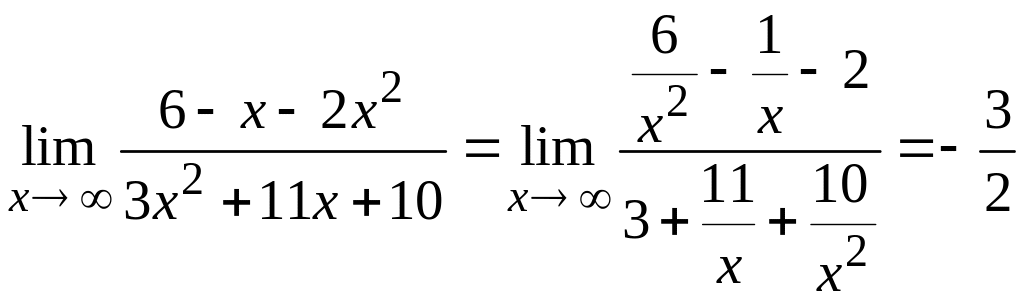 ,
,
так
как при
![]() каждая
из дробей
каждая
из дробей
![]()
![]()
![]()
![]() стремится к нулю.
стремится к нулю.
2.
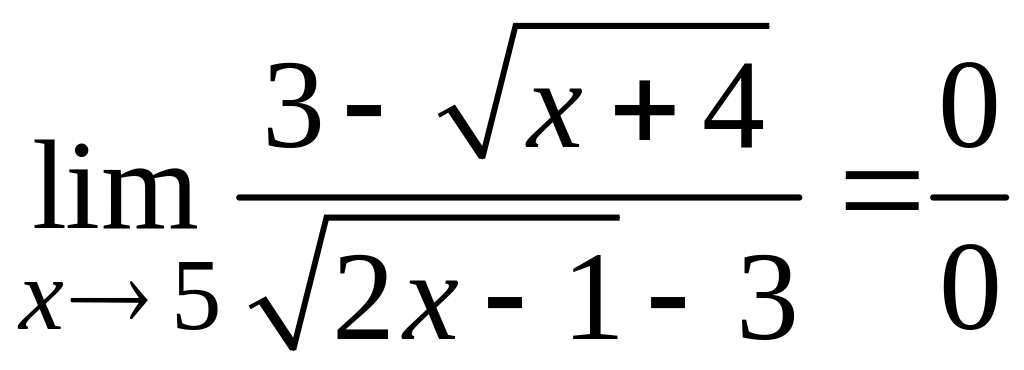 .
.
Здесь для освобождения от неопределенности умножим числитель и знаменатель дроби на сопряженные к ним выражения:
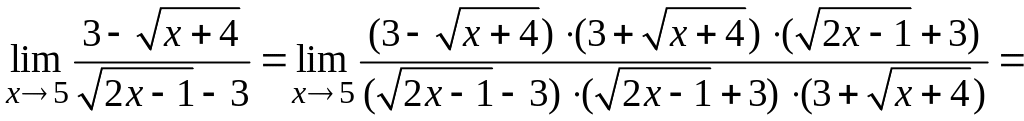
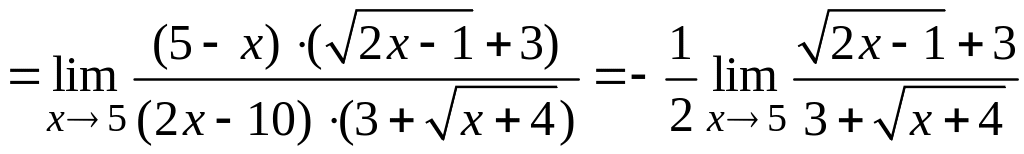 .
.
При
![]()
![]() ,
поэтому окончательно имеем
,
поэтому окончательно имеем
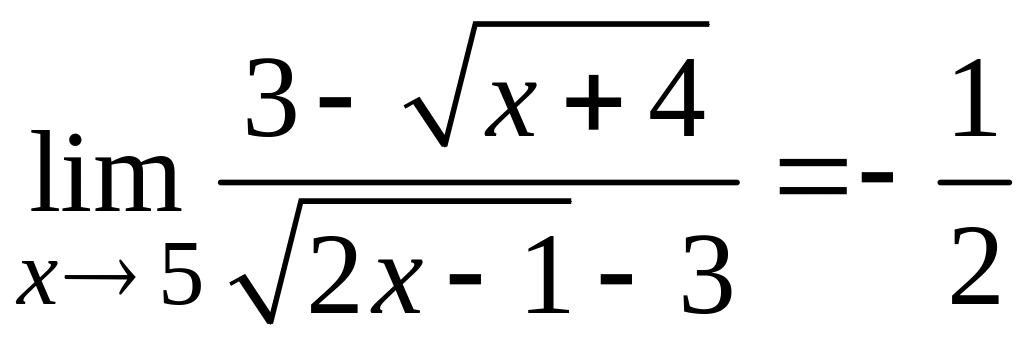 .
.
3.
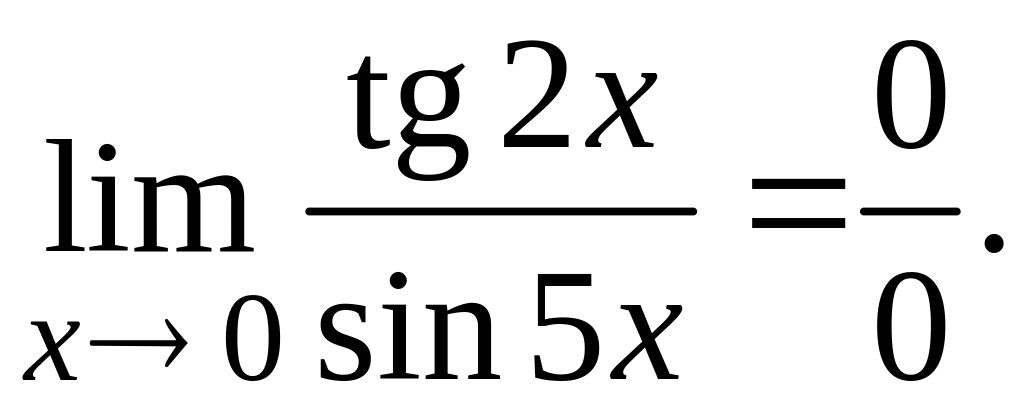
В
данном случае для освобождения от
неопределенности воспользуемся первым
замечательным пределом
 и его следствием
и его следствием
 .
Имеем
.
Имеем
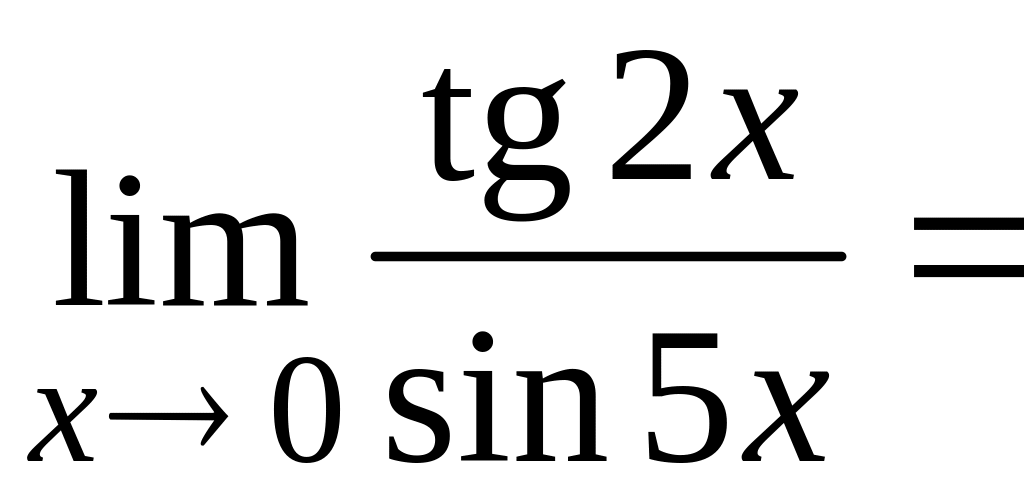
 =
=
II.
1. Опишем сначала область определения
заданной функции
![]() :
:
![]()
Теперь
возьмем произвольное значение
![]() и
дадим ему приращение
и
дадим ему приращение
![]() .
В результате получим новое значение
аргумента
.
В результате получим новое значение
аргумента
![]() ,
которому соответствует значение функции
,
которому соответствует значение функции
![]() .
.
Ищем
приращение функции
![]() ,
соответствующее приращению ее аргумента
в рассматриваемой точке
,
соответствующее приращению ее аргумента
в рассматриваемой точке
![]() :
:
![]()
![]()
![]() .
.
Проверяем выполнение первого определения непрерывности функции в точке :
![]() .
.
Определение
выполнено. Функция непрерывна в точке
.
Поскольку по предположению
является произвольной точкой
![]() ,
то доказана непрерывность функции во
всей ее области определения.
,
то доказана непрерывность функции во
всей ее области определения.
2.
Поступаем аналогично в случае функции

Берем произвольное значение x:
![]() .
.
Даем
ему приращение
и получаем соответствующее приращение
функции:
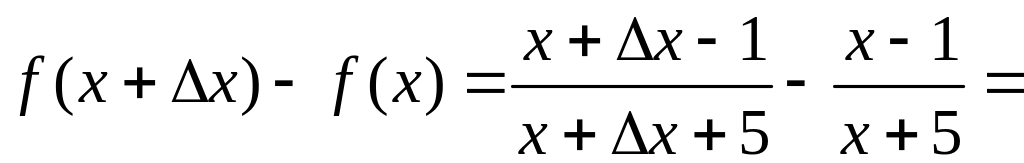
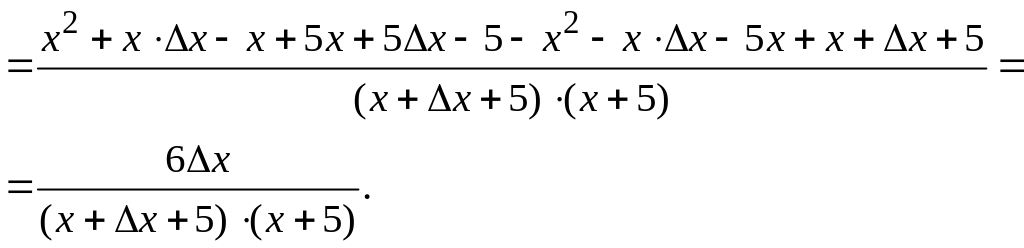
Проверяем выполнение первого определения непрерывности функции в точке :
 .
.
Доказательство непрерывности функции во всей ее области определения завершено.
III.
1.

Функция
имеет точку разрыва
![]() .
Классифицируем ее, вычисляя односторонние
пределы.
.
Классифицируем ее, вычисляя односторонние
пределы.
 .
Здесь при
.
Здесь при
![]() имеем:
имеем:

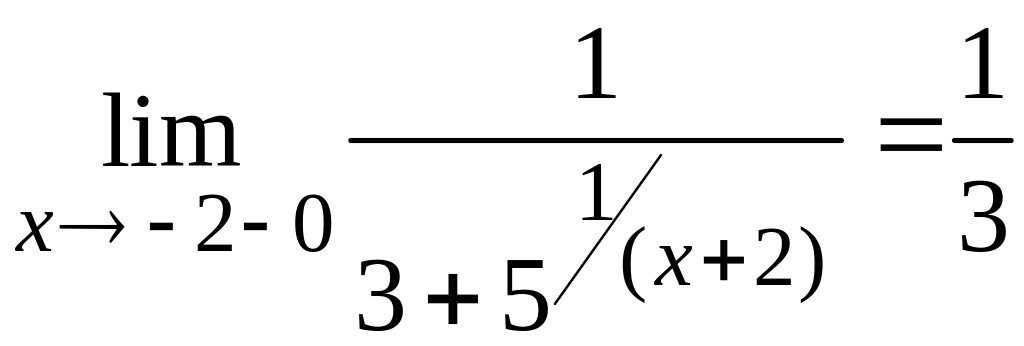 .
.
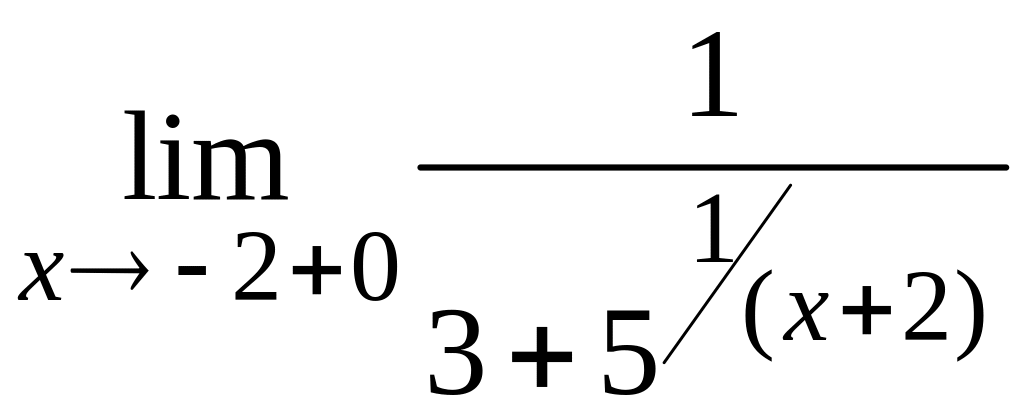 .
Здесь при
.
Здесь при
![]() имеем:
имеем:
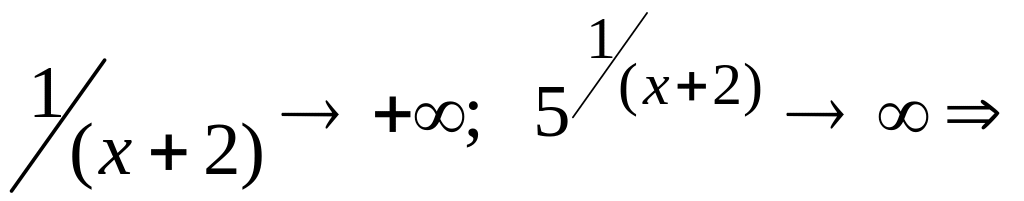
 .
.
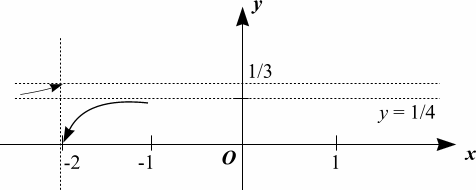
Таким образом, точка является точкой разрыва первого рода заданной функции и график функции вертикальных асимптот не имеет.
Поскольку,
очевидно,
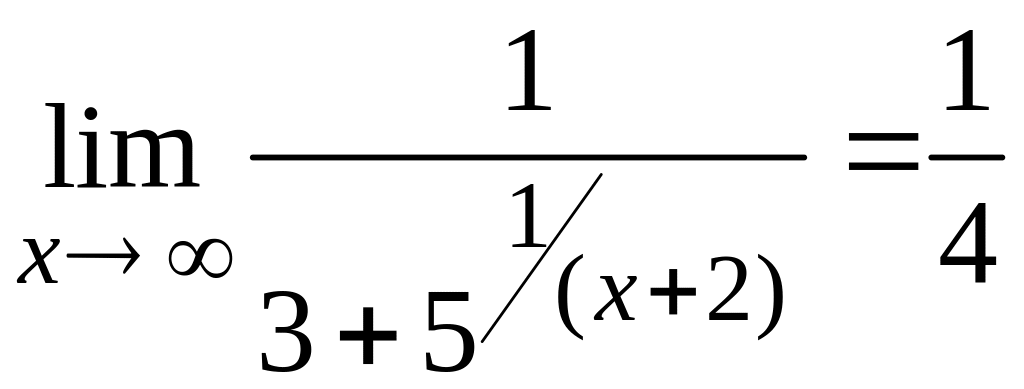 ,
то прямая
,
то прямая
 является горизонтальной асимптотой
графика.
является горизонтальной асимптотой
графика.
2.
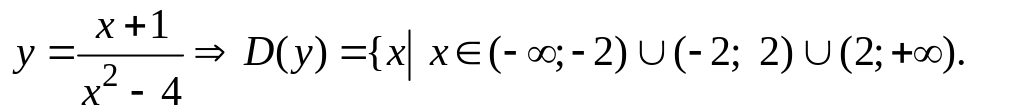
Классифицируем
точки разрыва функции
и
![]() .
.
 ,
так как при
,
так как при
![]() является положительной бесконечно
малой величиной.
является положительной бесконечно
малой величиной.
 ,
так как при
,
так как при
![]() является отрицательной бесконечно
малой величиной.
является отрицательной бесконечно
малой величиной.
 ,
так как при
,
так как при
![]() является отрицательной бесконечно
малой величиной.
является отрицательной бесконечно
малой величиной.
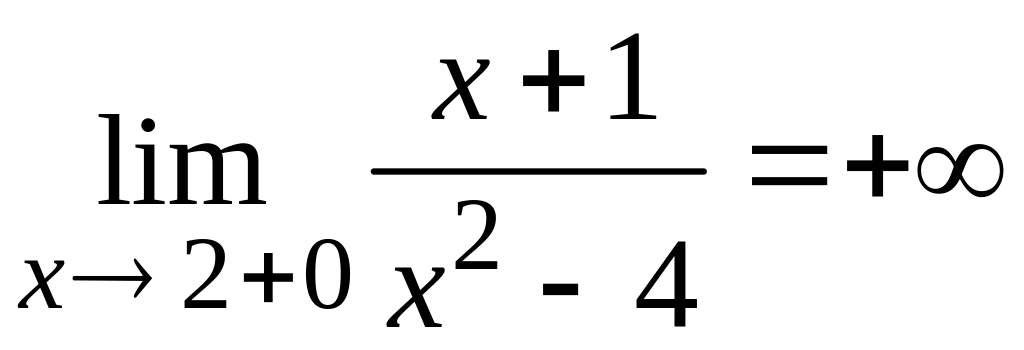 ,
так как при
,
так как при
![]() является положительной бесконечно
малой величиной.
является положительной бесконечно
малой величиной.
Таким образом, точки и являются точками разрыва второго рода заданной функции, а прямые и вертикальными асимптотами ее графика.
Поскольку
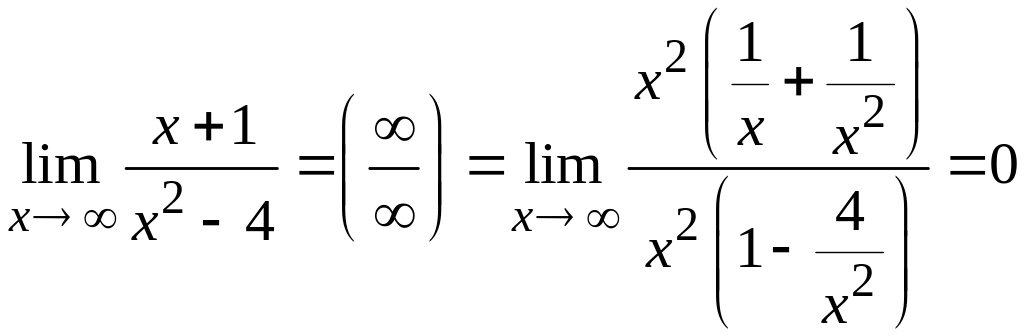 ,
то прямая
,
то прямая
![]() является горизонтальной асимптотой
графика.
является горизонтальной асимптотой
графика.

3.

Каждая ветвь заданной функции непрерывна. Точка разрыва может быть лишь на стыке этих ветвей. Вычисляем в нем односторонние пределы:
![]()
![]() ;
;
![]()
![]()
Таким
образом,
![]() является точкой разрыва первого рода
заданной функции. Вертикальных асимптот
график не имеет. Очевидно, горизонтальных
асимптот у графика функции тоже нет,
т.к.
является точкой разрыва первого рода
заданной функции. Вертикальных асимптот
график не имеет. Очевидно, горизонтальных
асимптот у графика функции тоже нет,
т.к.
![]() const
при
const
при
![]() .
.
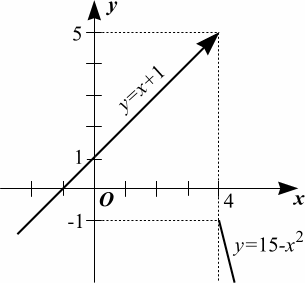
ПРИМЕР 2. Провести анализ и построить графики функций:
I.
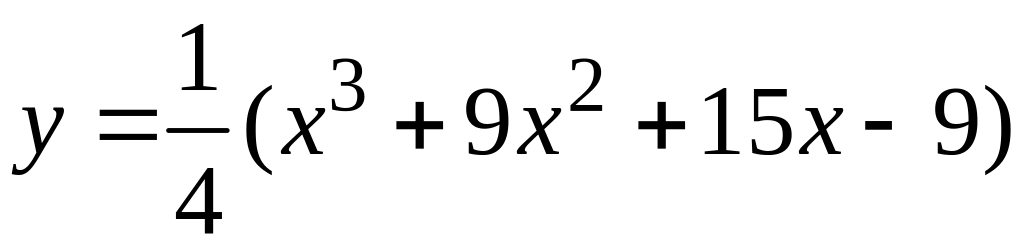 .
II.
.
II.
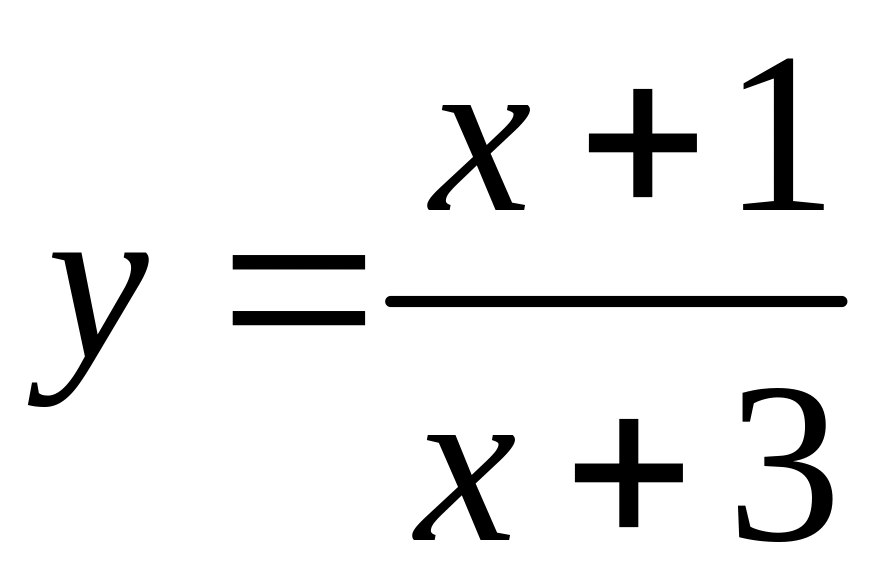 .
III.
.
III.
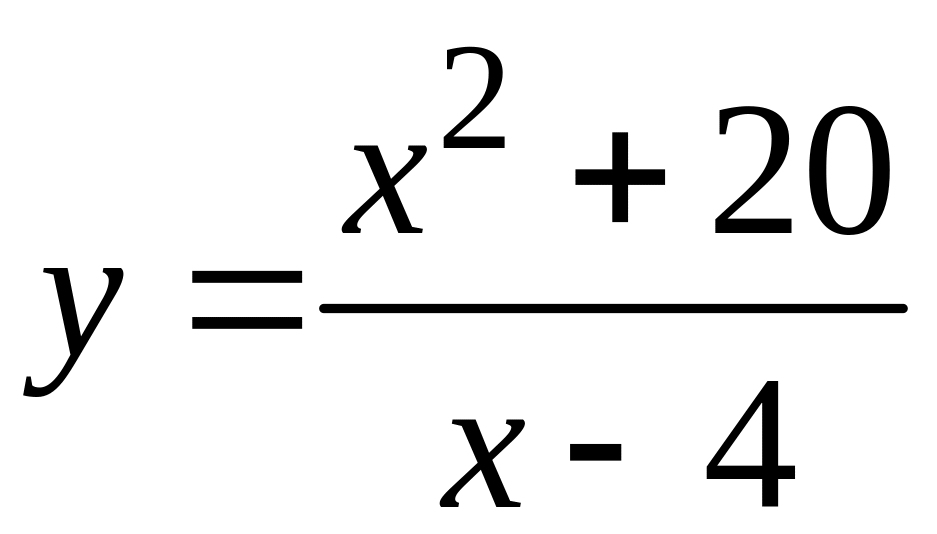 .
.
Решение.
I. .
1. Областью определения данной функции являются все действительные значения аргумента , то есть
![]() .
.
2. Функция непрерывна на всей числовой прямой, поэтому ее график не имеет вертикальных асимптот.
Выясним
наличие у графика заданной функции
наклонных асимптот. Для определения
параметров уравнения асимптоты
![]() воспользуемся формулами
воспользуемся формулами
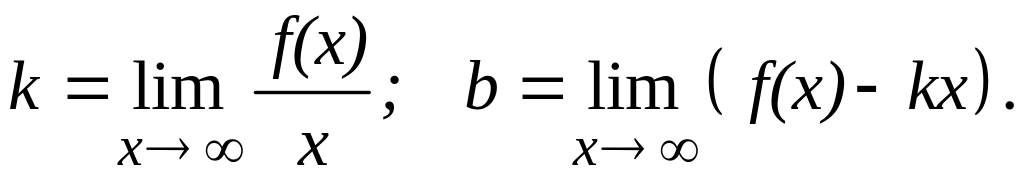
Имеем

Таким образом, у графика заданной функции наклонных асимптот нет.
3.
Исследуем функцию на экстремумы и
интервалы монотонности. С этой целью
найдем ее производную и приравняем к
нулю:

Решая
полученное квадратное уравнение, делаем
вывод о том, что функция имеет две
критические точки первого рода
![]() .
.
Разбиваем область определения этими точками на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:
|
|
|
|
|
|
|
+ |
|
– |
|
+ |
|
|
max |
|
min |
|
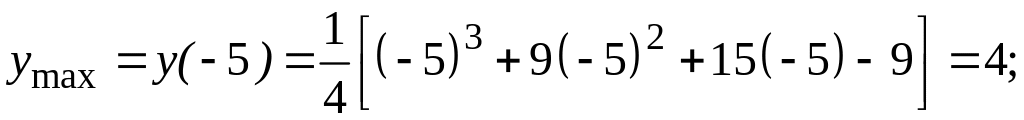
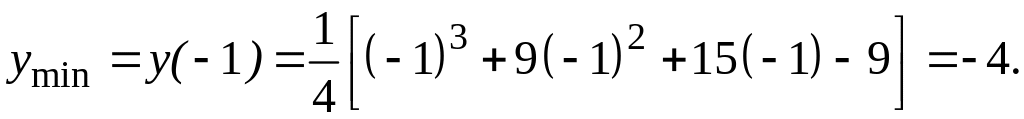
4. Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

Итак,
функция имеет одну критическую точку
второго рода
![]() .
Разобьем область определения полученной
точкой на части, в каждой из которых
установим знак второй производной:
.
Разобьем область определения полученной
точкой на части, в каждой из которых
установим знак второй производной:
|
|
|
|
|
|
0 |
+ |
|
|
т.п. |
|
Значение является абсциссой точки перегиба графика функции, а ордината этой точки
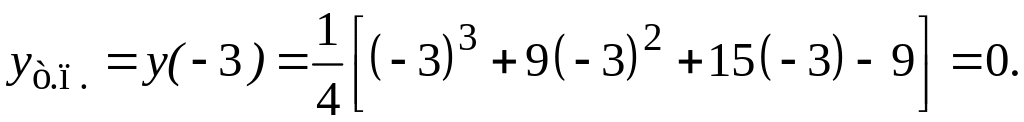
5.
Для построения графика в выбранной
системе координат изобразим точки
максимума
![]() ,
минимума
,
минимума
![]() ,
перегиба
,
перегиба
![]() ,
и точку
,
и точку
![]() пересечения графика с осью
пересечения графика с осью
![]() .
С учетом результатов предыдущих
исследований построим кривую:
.
С учетом результатов предыдущих
исследований построим кривую:

II.
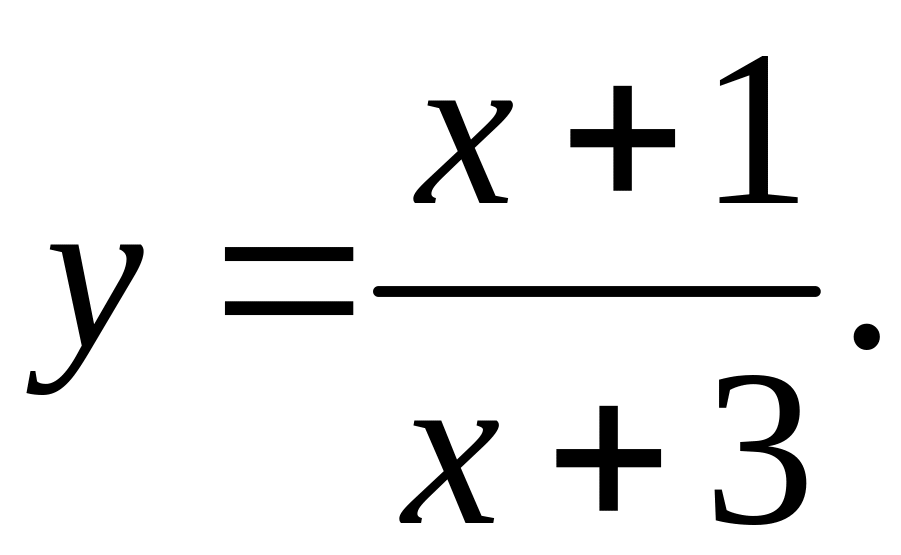
1. Область определения.
![]()
2. Исследование на непрерывность и асимптоты.
Заданная функция непрерывна всюду, кроме точки . Вычислим ее односторонние пределы в этой точке:
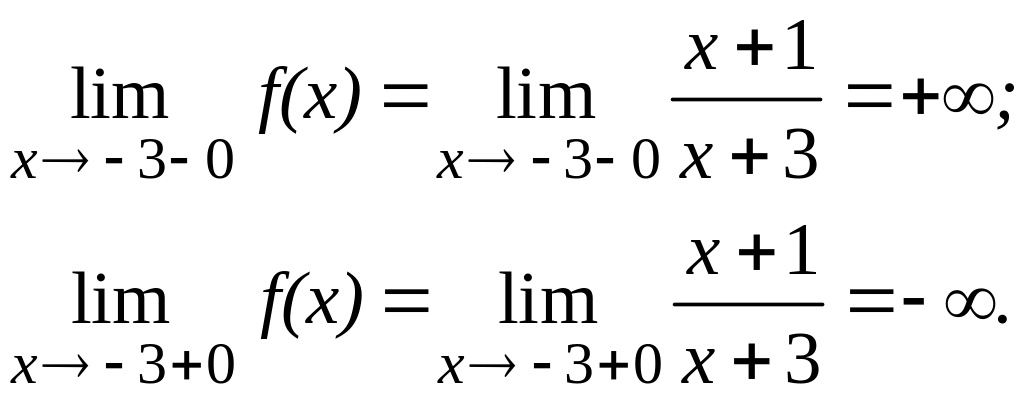
Итак, точка – точка разрыва второго рода заданной функции, а прямая – вертикальная асимптота графика.
Исследуем график на наличие наклонных асимптот.
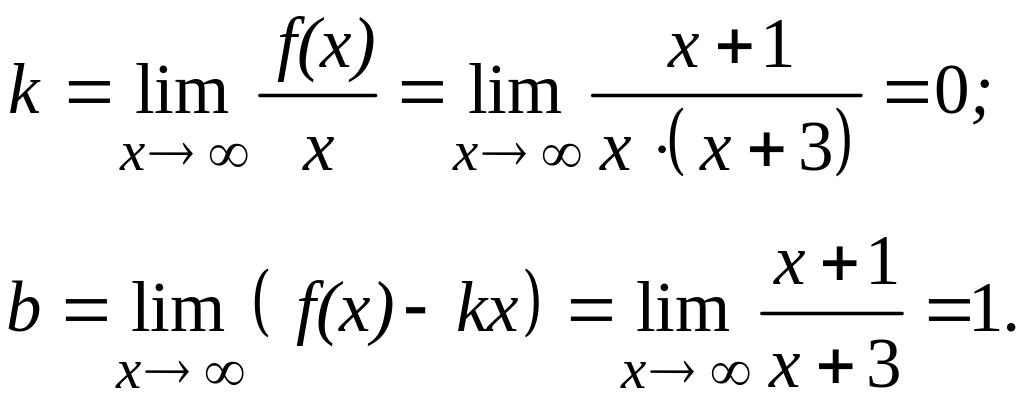
Таким
образом, прямая
![]() является горизонтальной асимптотой
графика.
является горизонтальной асимптотой
графика.
3. Исследование на экстремум и промежутки монотонности.

Поскольку
 то функция не имеет точек экстремума.
Так как
то функция не имеет точек экстремума.
Так как
![]() для всех точек из
,
то функция возрастает во всей области
определения.
для всех точек из
,
то функция возрастает во всей области
определения.
4. Исследование графика на выпуклость, вогнутость, точки перегиба.
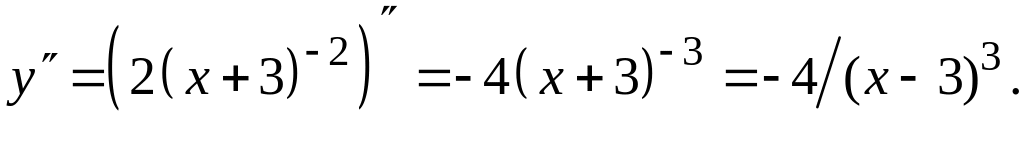
Поскольку
![]() ,
график не имеет точек перегиба.
,
график не имеет точек перегиба.
Очевидно,
что при
![]() ,
а при
,
а при
![]() .
Следовательно, график функции вогнутый
при
.
Следовательно, график функции вогнутый
при
![]() и выпуклый при
и выпуклый при
![]() .
.
5. Построение графика.

III. .
1.
Область определения
![]()
2. Исследование на непрерывность и асимптоты.
Заданная функция непрерывна всюду, кроме точки . Вычисляем односторонние пределы функции в этой точке:
 ;
;
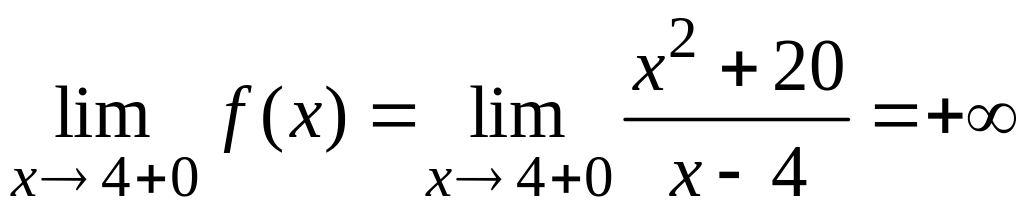 .
.
Таким образом, точка является для заданной функции точкой разрыва второго рода, а прямая – вертикальной асимптотой ее графика.
Исследуем график на наличие наклонных асимптот.
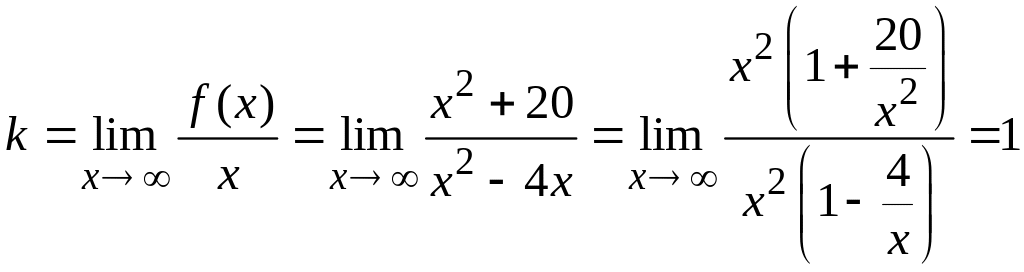 ;
;
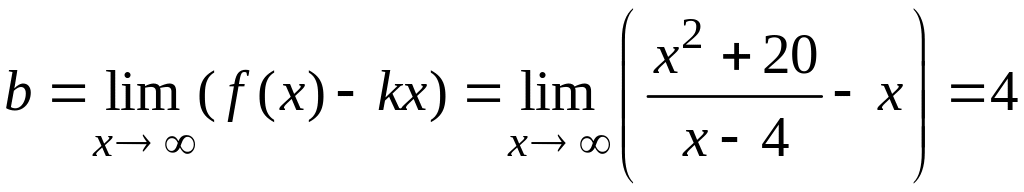 .
.
Вывод:
прямая
![]() –
наклонная асимптота графика.
–
наклонная асимптота графика.
3. Исследование функции на экстремум и промежутки монотонности.
 ;
;
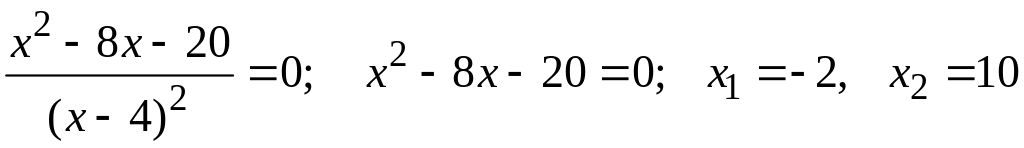 .
.
|
|
-2 |
(-2; 4) |
4 |
(4; 10) |
10 |
|
|
+ |
0 |
– |
не сущ. |
– |
0 |
+ |
|
|
max |
|
|
|
min |
|
![]()
4. Исследование графика функции на выпуклость, вогнутость, точки перегиба.

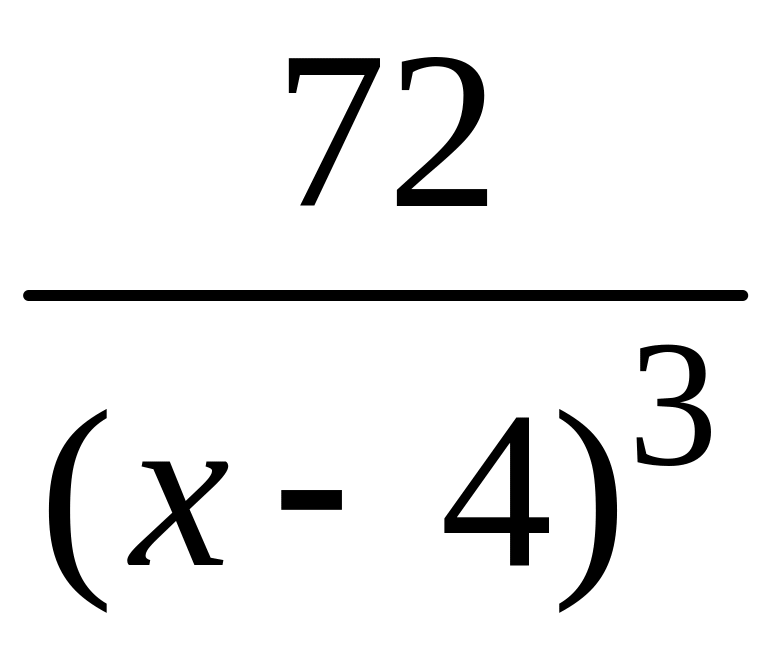 .
.
Так
как
![]() ,
то график заданной функции точек перегиба
не имеет. Остается выяснить вопрос об
интервалах его выпуклости и вогнутости:
,
то график заданной функции точек перегиба
не имеет. Остается выяснить вопрос об
интервалах его выпуклости и вогнутости:
|
|
4 |
|
|
– |
не сущ. |
+ |
|
|
|
|
Построение графика.