m32352_2

ПРИМЕР 2. Даны координаты вершин пирамиды ABCD:

Требуется:

1. записать векторы в системе орт и найти модули этих векторов;

2. найти угол между векторами и (в градусах, минутах, секундах);

3. найти проекцию вектора на вектор ;

4. найти площадь грани ;

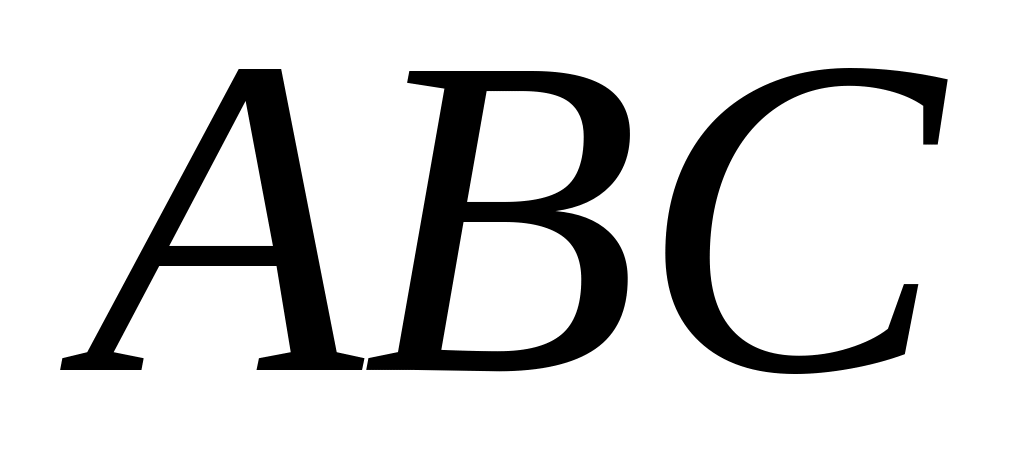5. составить уравнение ребра ;

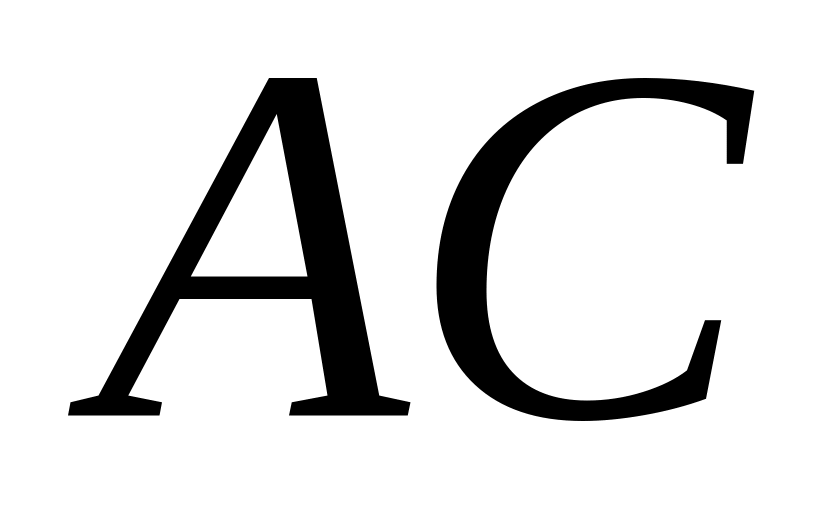6. составить уравнение грани ;

7. составить уравнение высоты пирамиды, проведенной из вершины , и найти координаты точки М ее пересечения с гранью ;

8. найти длину полученной высоты и объем пирамиды ABCD.

Решение.

1) Известно, что произвольный вектор представляется в системе орт , , по формуле

, (1.5)

где – координаты вектора в системе координат , порожденной ортами, причем

.

Если заданы точки и , то

. (1.6)

Воспользовавшись формулой (1.6) и координатами заданных точек, получим

Если вектор задан формулой (1.5), то его модуль вычисляется следующим образом:

. (1.7)

Используя формулу (1.7), получаем модули найденных векторов:

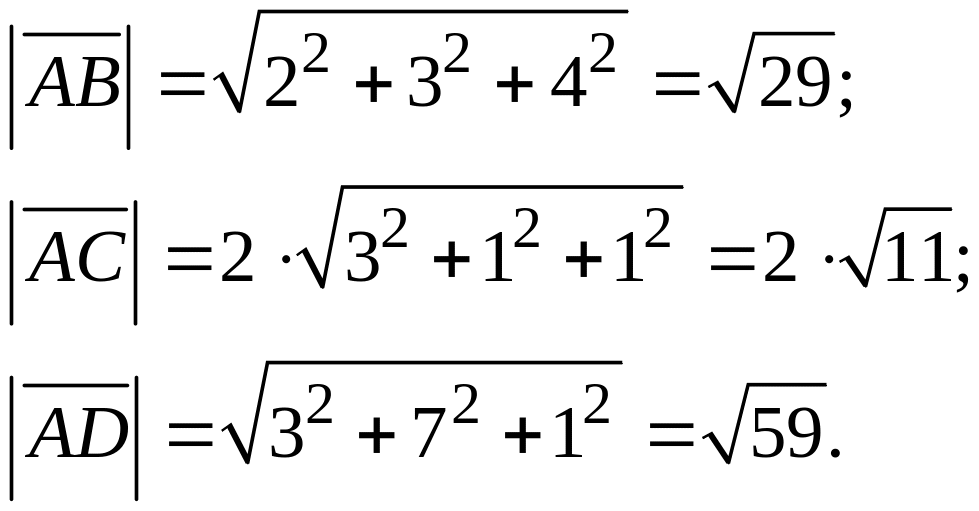
2) Воспользуемся формулой

,

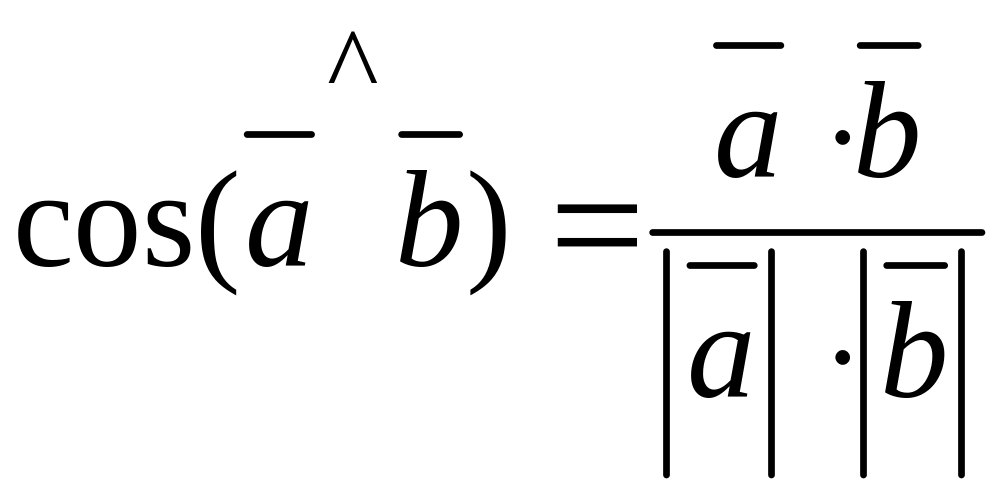где – скалярное произведение векторов и , которое вычисляется следующим образом:

У нас

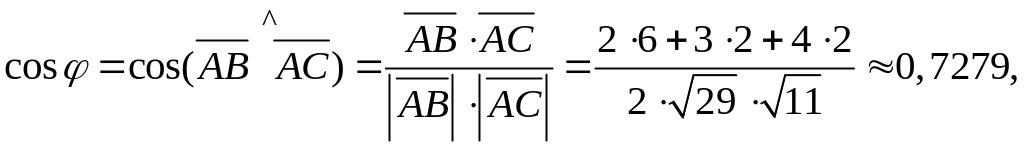
то есть .

3) Известно, что

,

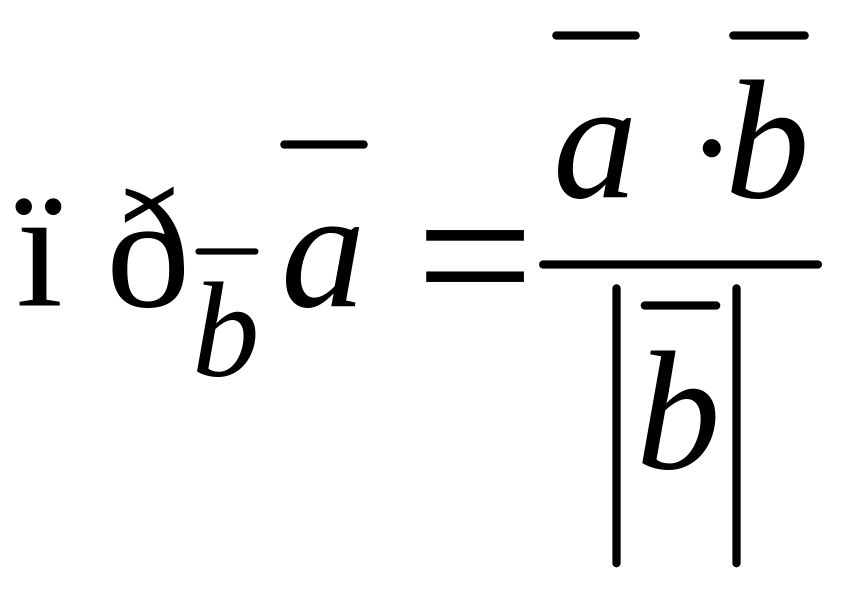то есть в нашем случае

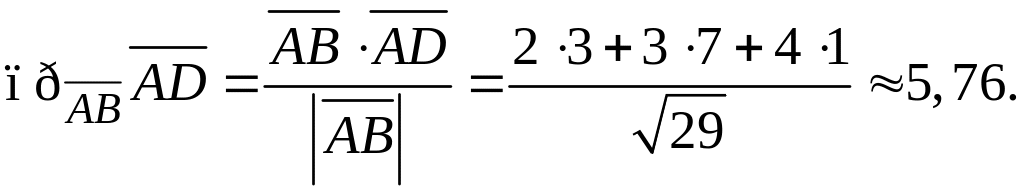
4) Воспользуемся формулой для нахождения площади треугольника, построенного на векторах и :

,

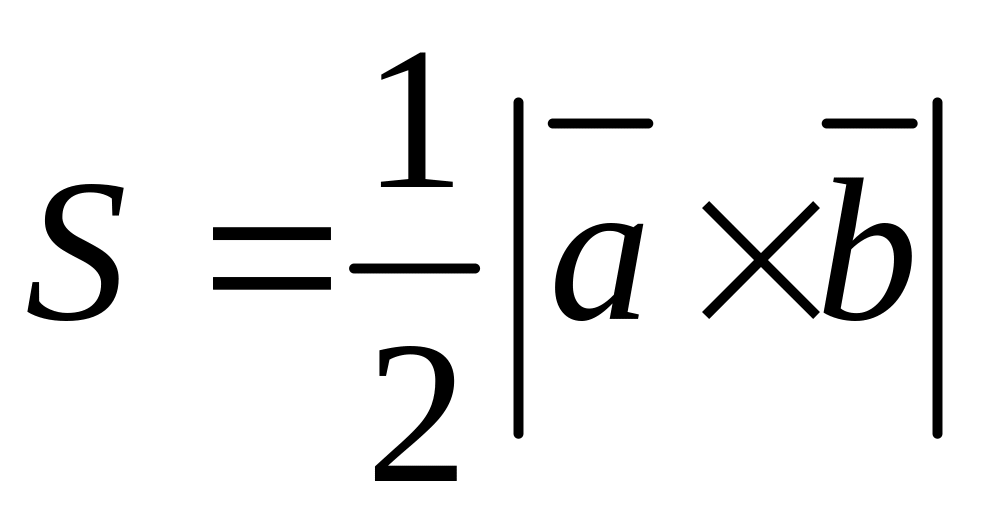где – векторное произведение векторов, которое вычисляется по следующему правилу:

.

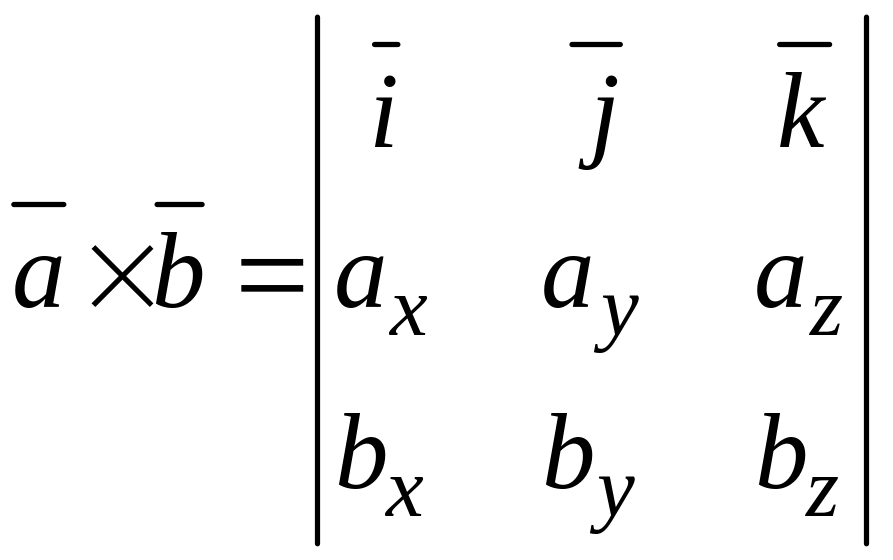В нашем примере 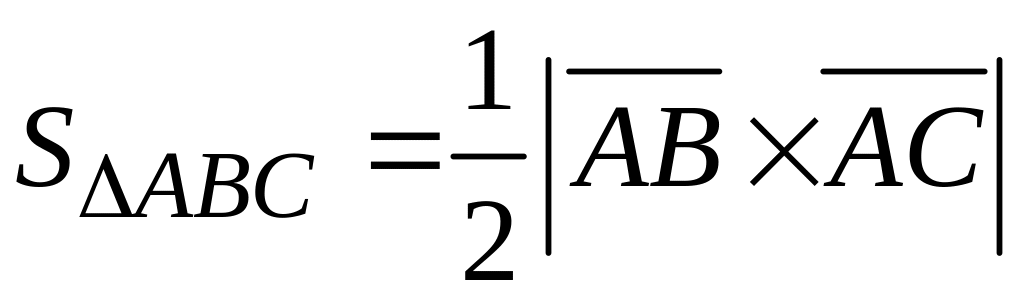, причем

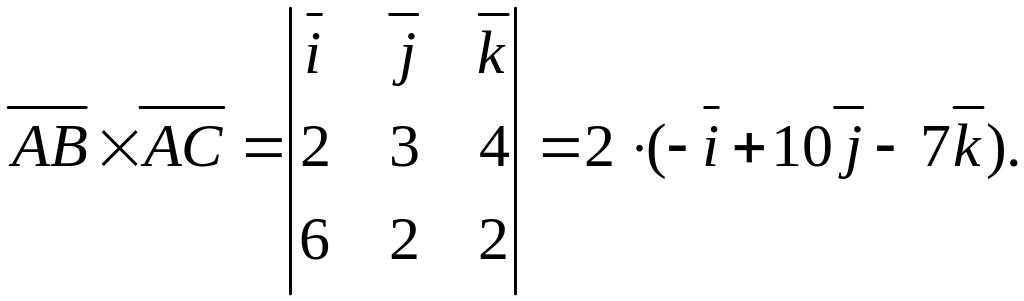
Таким образом,

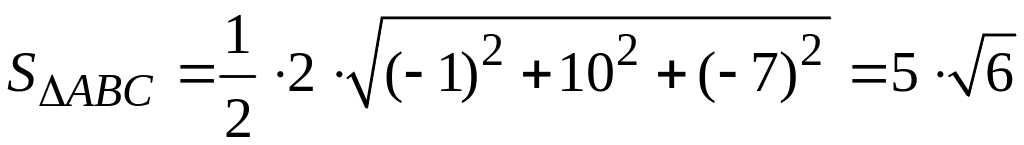(кв.ед.).

5) Для составления уравнений ребра АС пирамиды воспользуемся каноническими уравнениями прямой в пространстве

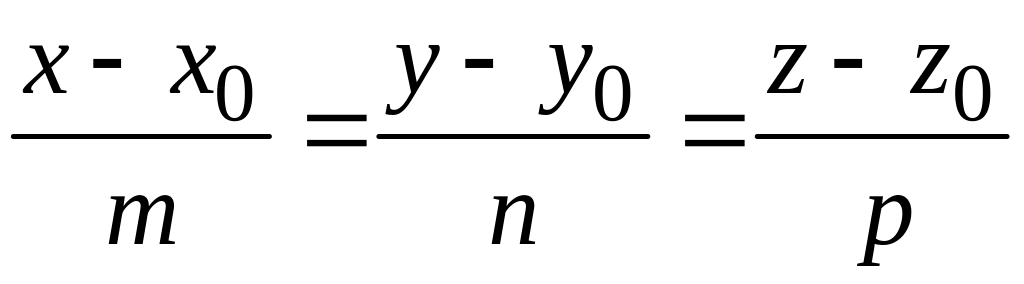, (1.8)

где точка, лежащая на прямой, а направляющий вектор прямой. В нашем случае можно положить , а Тогда из (1.8) получаем

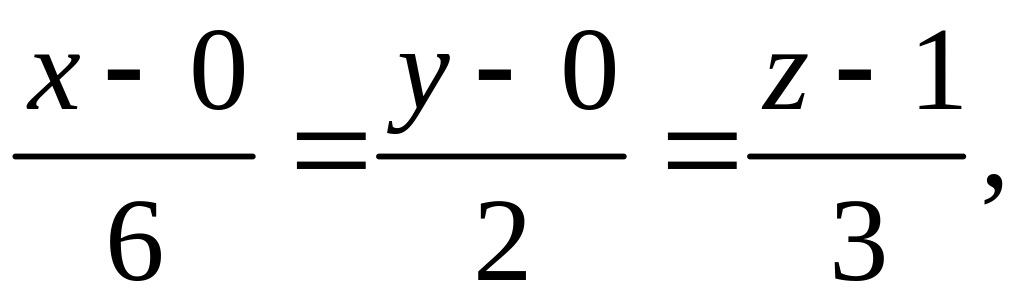
то есть уравнение ребра окончательно запишется следующим образом:

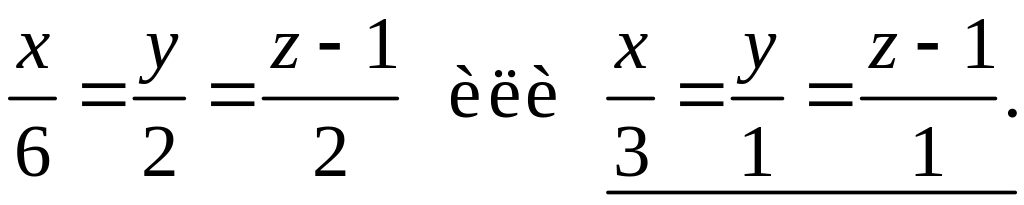
6) Уравнение плоскости, проходящей через три заданные точки , можно получить следующим образом: сначала найдем нормальный вектор плоскости как векторное произведение любой пары векторов, соединяющих заданные точки, а затем воспользуемся уравнением плоскости, проходящей через заданную точку, например, с известным нормальным вектором :

. (1.9)

В качестве нормального вектора грани АВС можно взять вектор , найденный ранее, или вектор . Итак, назначим , а . Тогда из уравнения (1.9) получаем искомое уравнение грани АВС:

.

7) Нормальный вектор грани АВС является, очевидно, направляющим вектором высоты пирамиды, опущенной на грань АВС из вершины D. Для составления искомого уравнения высоты остается воспользоваться каноническими уравнениями (1.8), где , а :

.

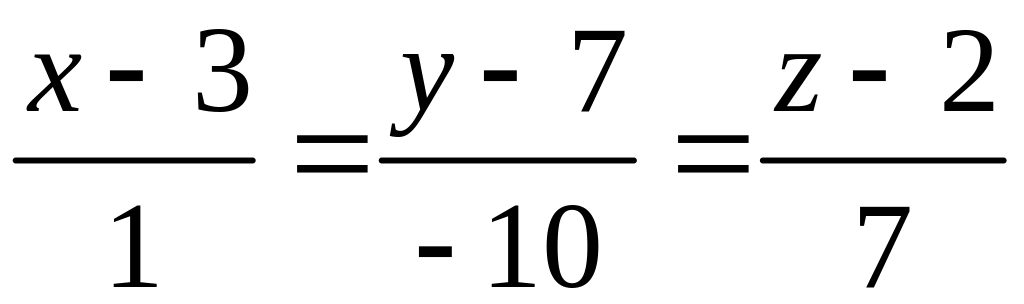Для нахождения координат точки М пересечения полученной высоты с гранью АВС перейдем от канонических уравнений высоты к параметрическим и решим их совместно с уравнением грани:



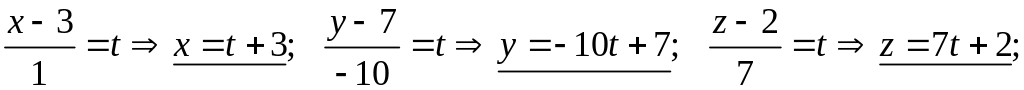
это значение параметра t, соответствующее искомой точке М. Для получения координат точки М подставим найденное значение параметра в параметрические уравнения высоты, в результате чего будем иметь .

8) Найдем длину высоты DM двумя способами: как расстояние между точками D и M и как расстояние от точки D до плоскости АВС.

Способ 1. .

Способ 2. Расстояние от точки до плоскости с уравнением вычисляется по формуле

.

В нашем случае , уравнение плоскости (грани АВС) , поэтому

.

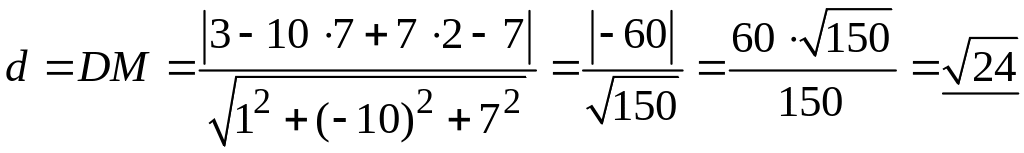Объем пирамиды ABCD можно найти по известной формуле: . В нашем случае имеем:

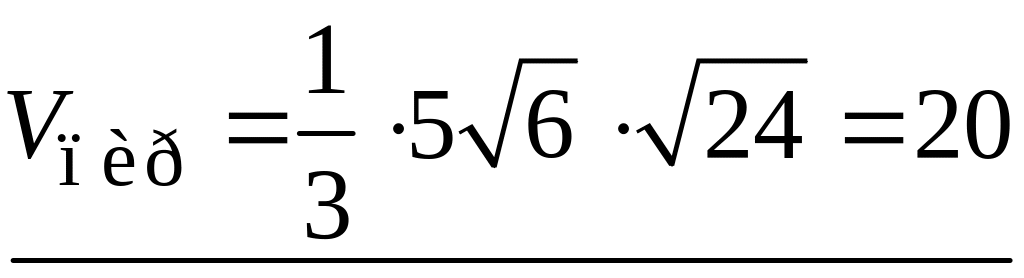(куб. ед.).

ПРИМЕР 3. Составить уравнение линии, для каждой точки которой ее расстояние до точки равно расстоянию до прямой Полученную кривую построить в системе координат.

Решение. Пусть – текущая точка искомой кривой. Опустим из точки перпендикуляр на прямую (рис. 1.2). Тогда . Так как , то

.

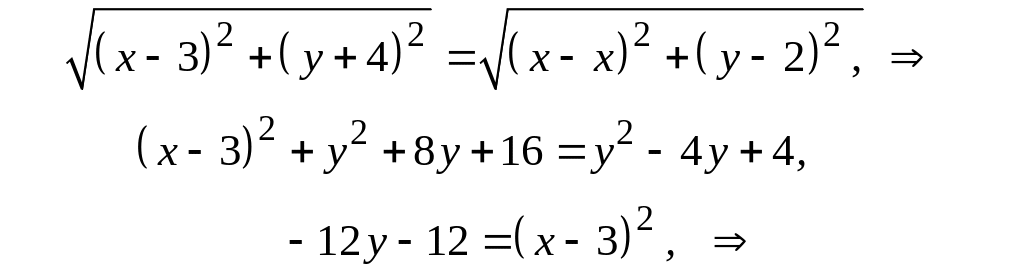
Полученное уравнение определяет параболу с вершиной в точке и ветвями, направленными вниз (см. рис. 1.2).

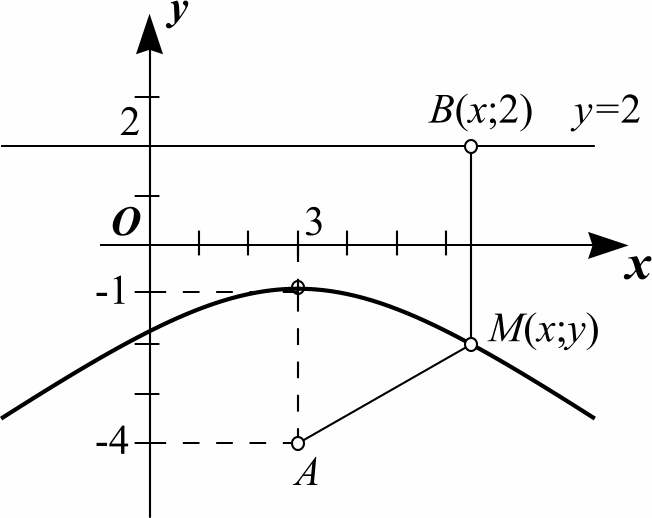
Рис. 1.2

ПРИМЕР 4. Составить уравнение линии, являющейся геометрическим местом точек, сумма расстояний от каждой из которых до точек и постоянна и равна .

Решение. Возьмем произвольную точку кривой М(x; y) и соединим ее отрезками прямых с точками А и В. По условию при этом выполняется равенство МА + МВ = . Распишем его в координатах и проведем тождественные преобразования:

=

.

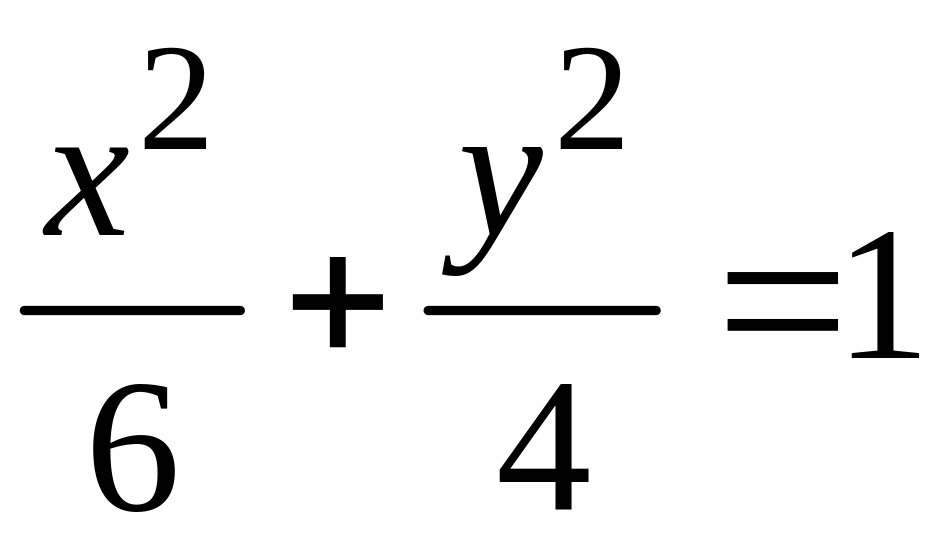Получили каноническое уравнение эллипса с центром симметрии в начале координат. Большая и малая полуоси эллипса равны соответственно и 2, а фокусы находятся в ранее заданных точках и (рис. 1.3).

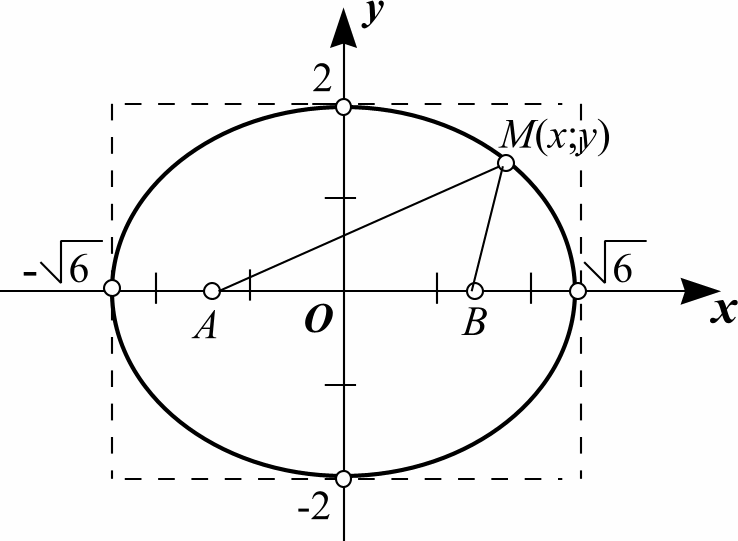
Рис. 1.3

ПРИМЕР 5. Составить уравнение линии, являющейся геометрическим местом точек, разность расстояний от каждой из которых до точек и постоянна и равна .

Решение. Возьмем произвольную точку кривой М(x; y) и соединим ее отрезками прямых с точками C и D. По условию при этом выполняется равенство МC  МD = . Распишем его в координатах и проведем тождественные преобразования:

=

.

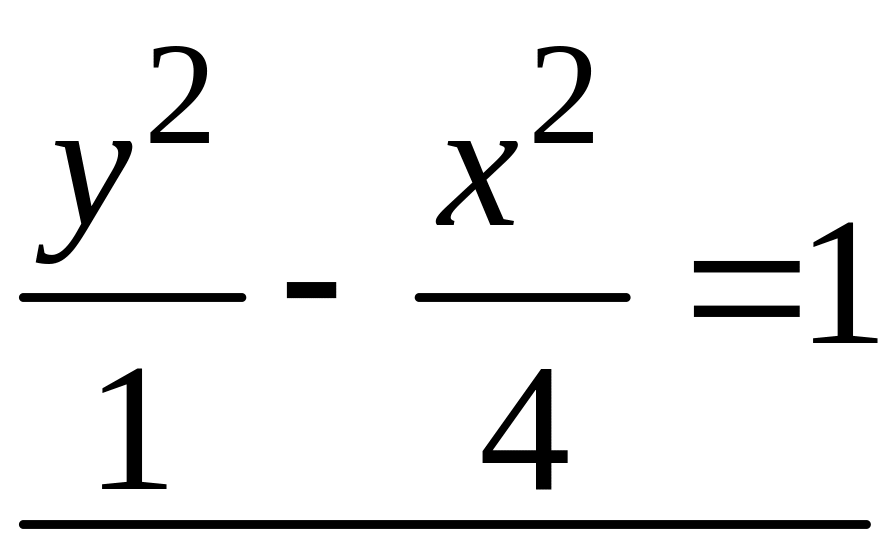Получили каноническое уравнение гиперболы с центром симметрии в начале координат. Действительная и мнимая полуоси гиперболы равны соответственно 2 и 1, а фокусы находятся в ранее заданных точках и (рис. 1.4).

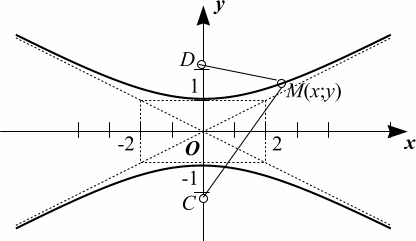
Рис. 1.4

22