
m32351_2
.docЭто значит, что прямая (l) и плоскость (Р) не являются ни параллельными, ни перпендикулярными.
Найдем точку пересечения прямой (l)
с плоскостью (Р). Для этого сначала
запишем канонические уравнения прямой
(l) в параметрической
форме:
![]() .
Имеем:
.
Имеем:
![]() .
.
Теперь решаем совместно параметрические уравнения прямой (l) и уравнение плоскости (Р):
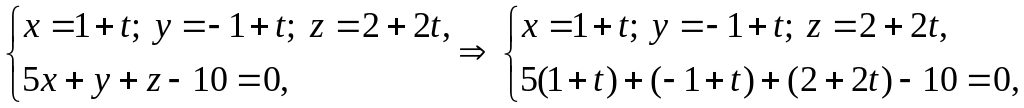
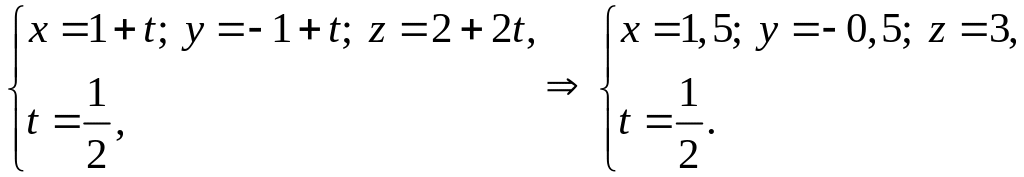
Вывод: прямая (l)
пересекается с плоскостью (Р) в точке
![]() .
.
Тема 2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Контрольные вопросы
Что называется матрицей порядка
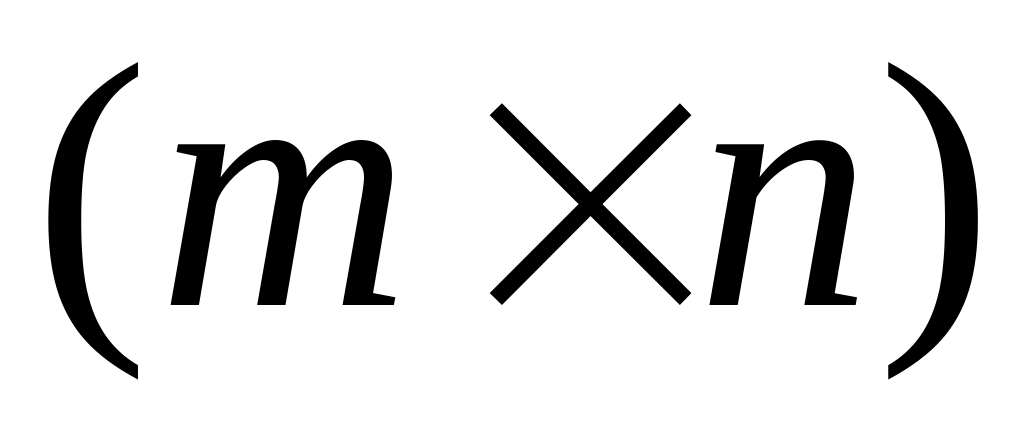 ?
?Какие действия можно выполнять с матрицами?
Как умножить матрицу на вектор-столбец? Как должны быть согласованы порядок матрицы и размерность столбца?
Как умножить матрицу на матрицу? Как должны быть согласованы порядки матриц?
Что понимают под определителем квадратной матрицы второго порядка? Третьего порядка?
Как определяется обратная матрица? Сформулируйте условие существования обратной матрицы.
Как записать систему линейных уравнений в матричной форме?
Напишите формулы Крамера для решения системы трех уравнений с тремя неизвестными.
З А Д А Ч И
ЗАДАЧА 2.1. Требуется:
Для заданных матриц
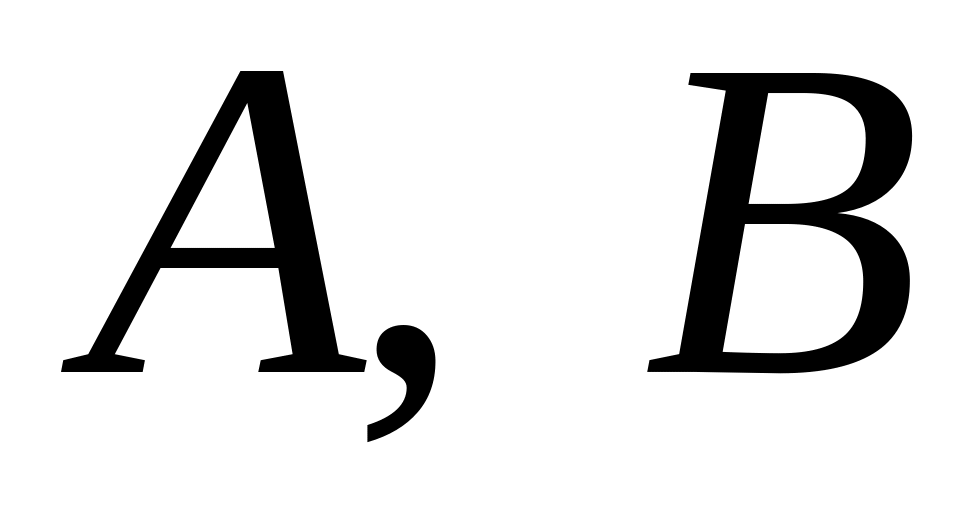 проверить, справедливо ли равенство
проверить, справедливо ли равенство
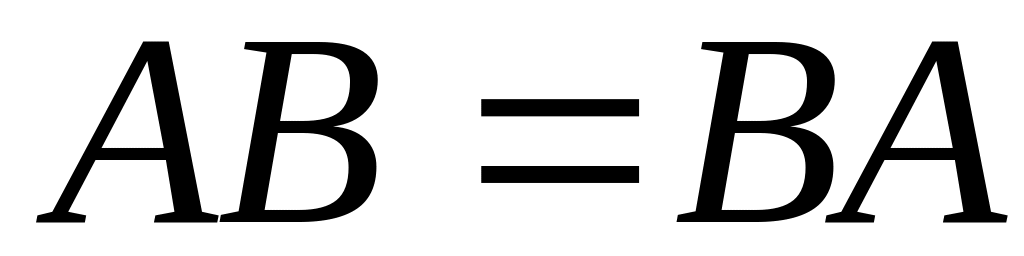 .
.Для заданных матриц
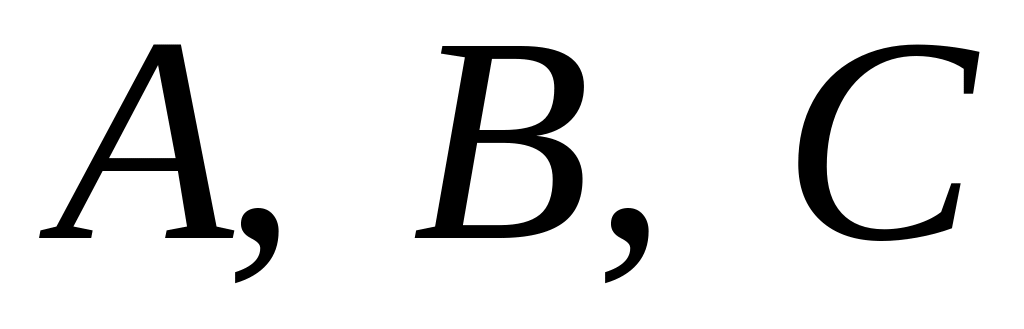 показать непосредственным вычислением,
что
показать непосредственным вычислением,
что
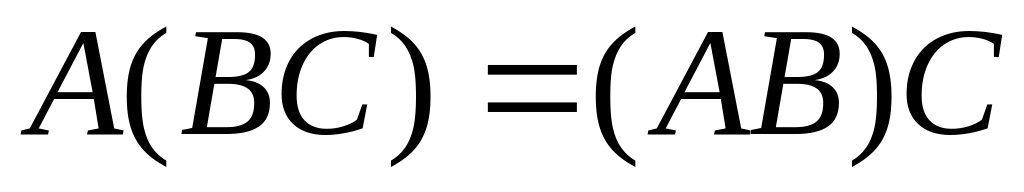 .
.Для заданных матриц показать непосредственным вычислением, что
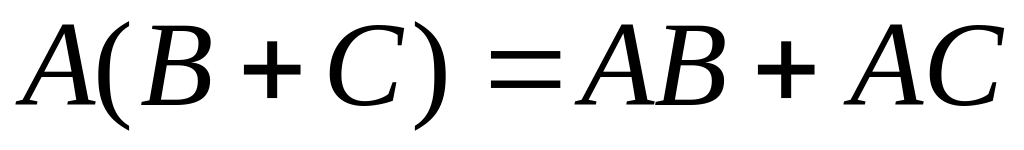 .
.Заданное матричное равенство записать как систему трех с тремя неизвестными
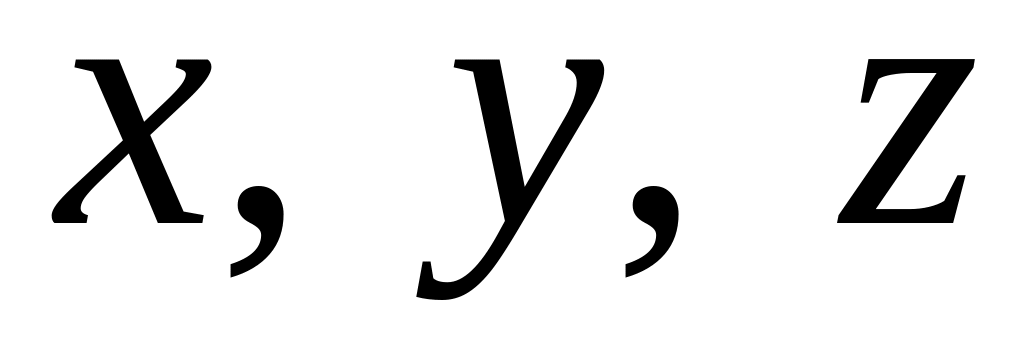 и решить ее а) с помощью формул Крамера;
б) методом Гаусса последовательного
исключения неизвестных.
и решить ее а) с помощью формул Крамера;
б) методом Гаусса последовательного
исключения неизвестных.
Вариант 1.
1.
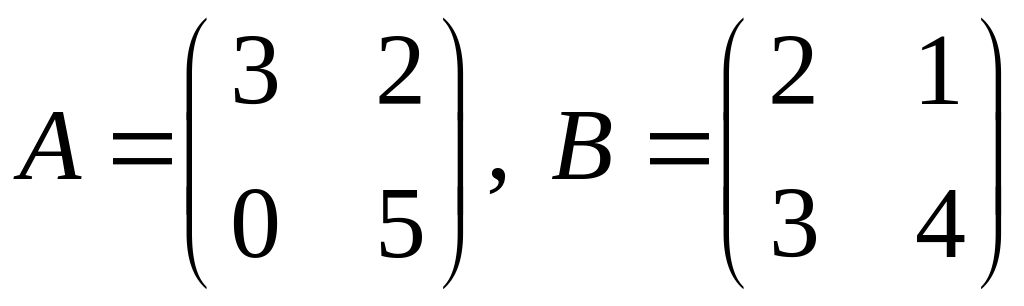 .
.
2.
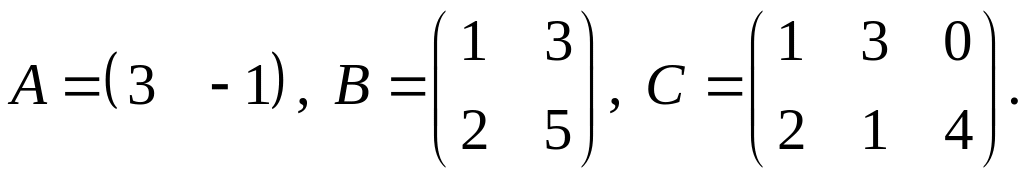
3.
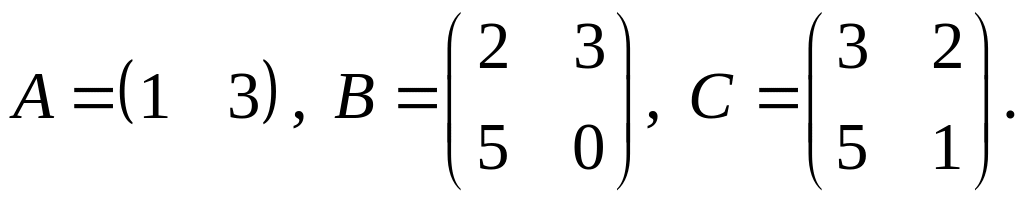
4.
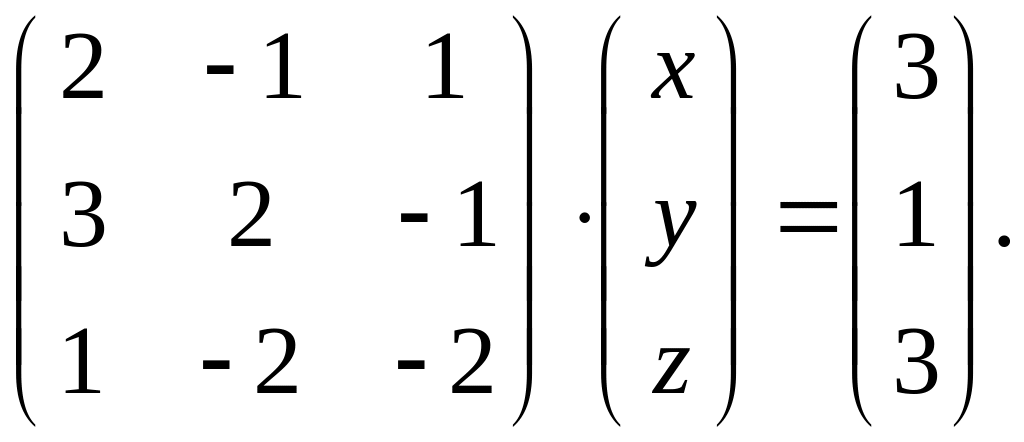
Вариант 2.
1.
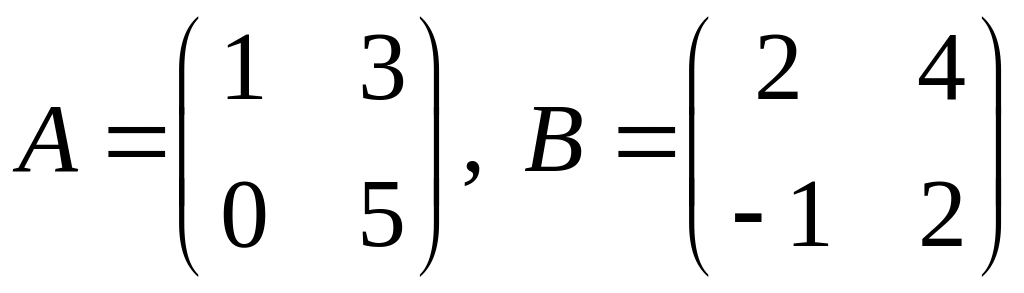 .
.
2.
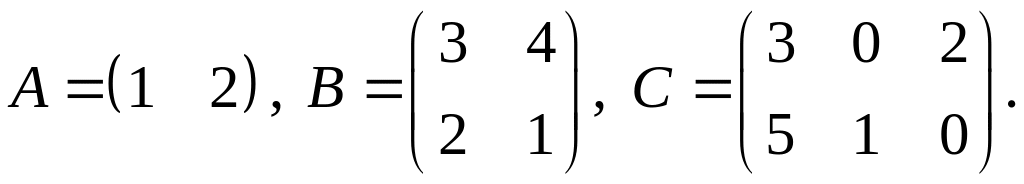
3.
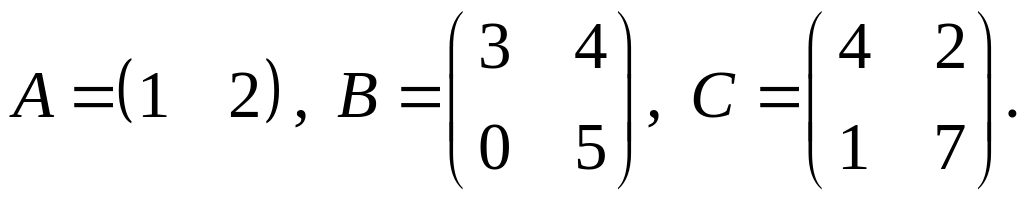
4.
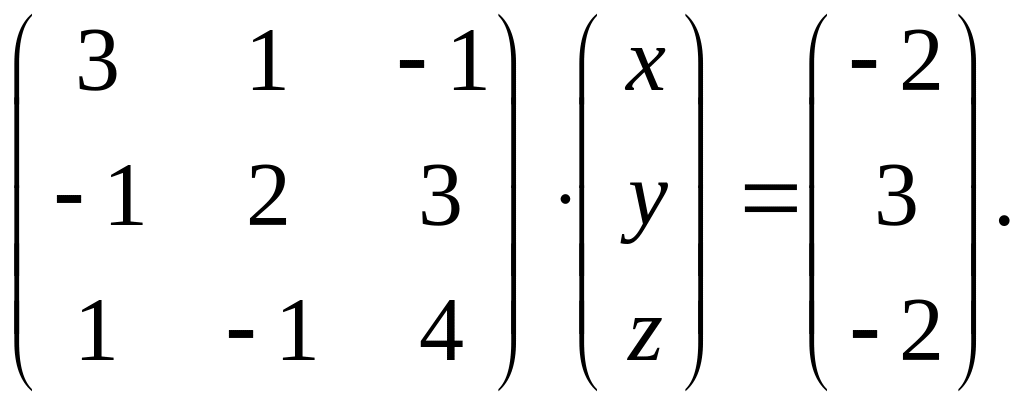
Вариант 3.
1.
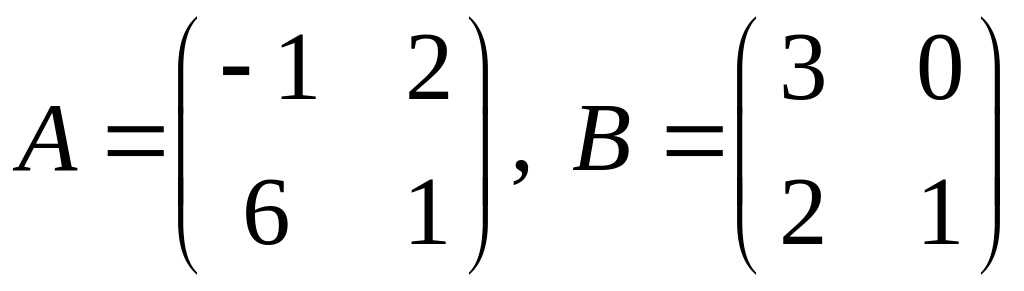 .
.
2.
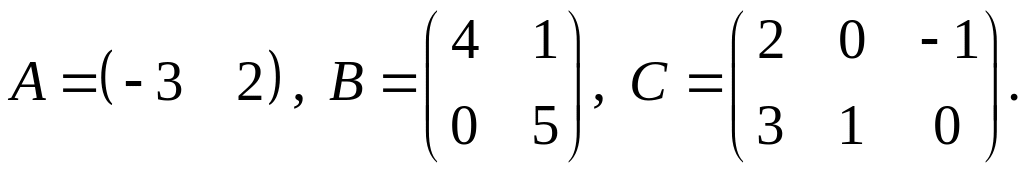
3.
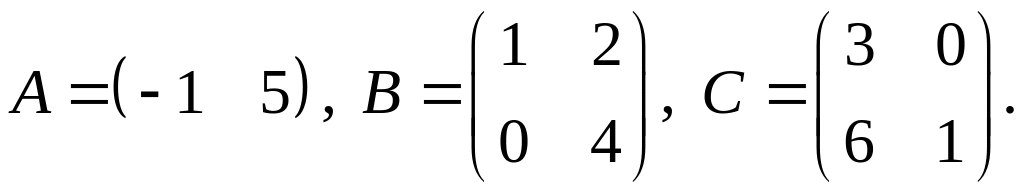
4.
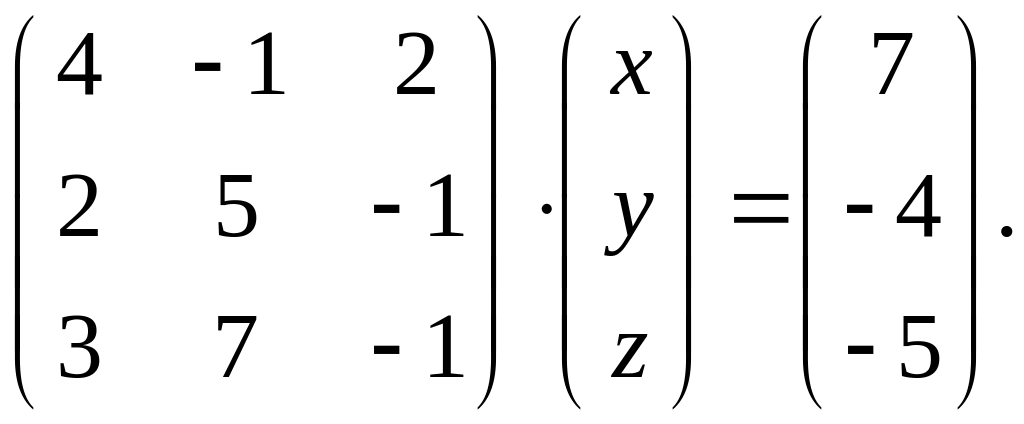
Вариант 4.
1.
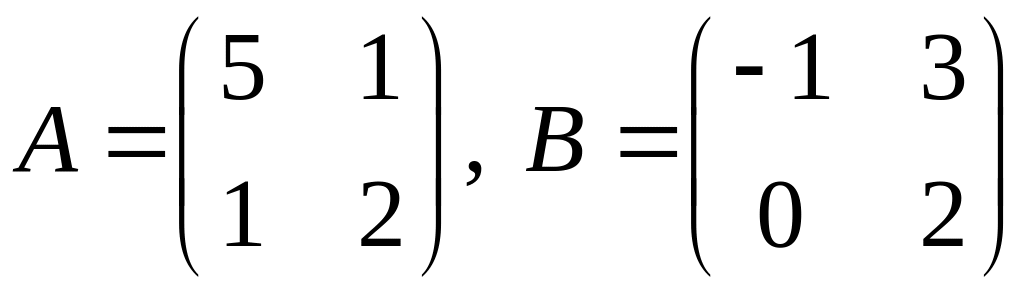 .
.
2.
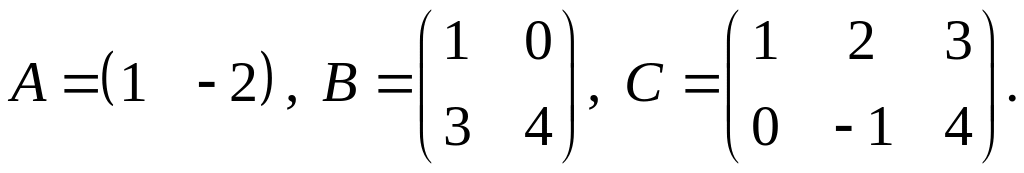
3.
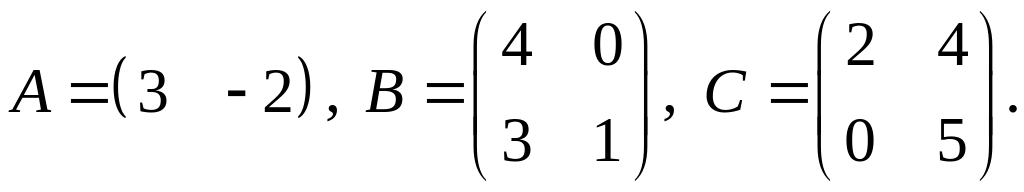
4.
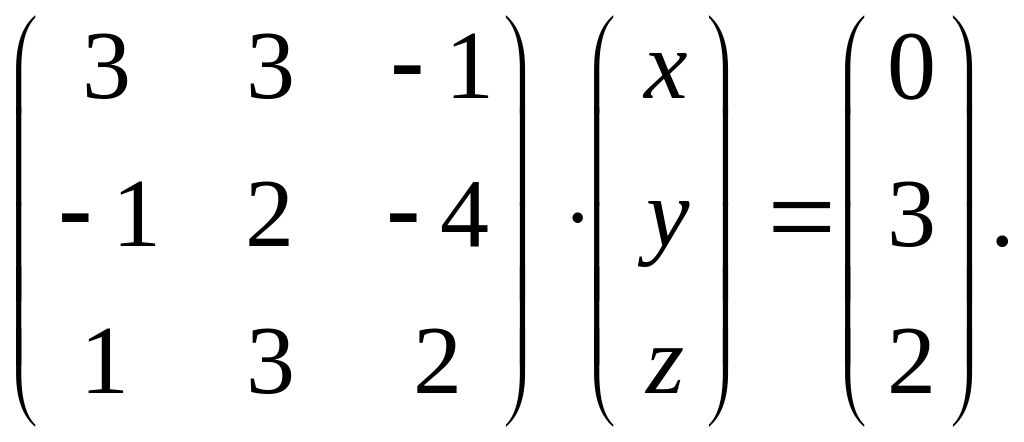
Вариант 5.
1.
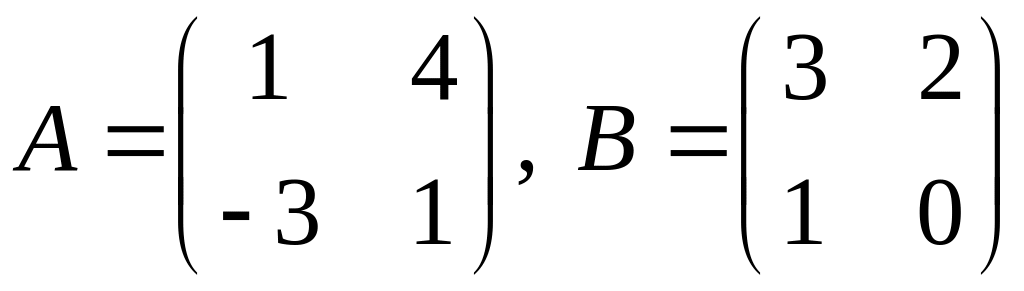 .
.
2.
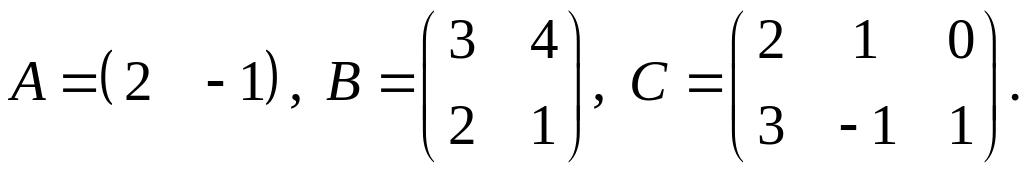
3.
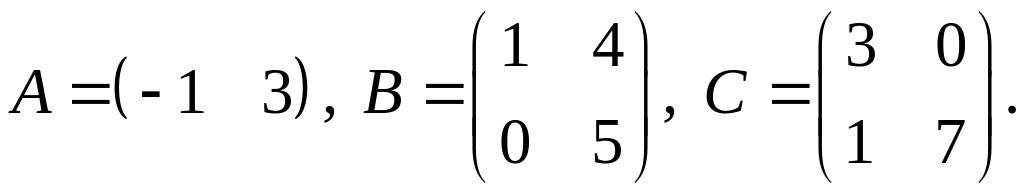
4.
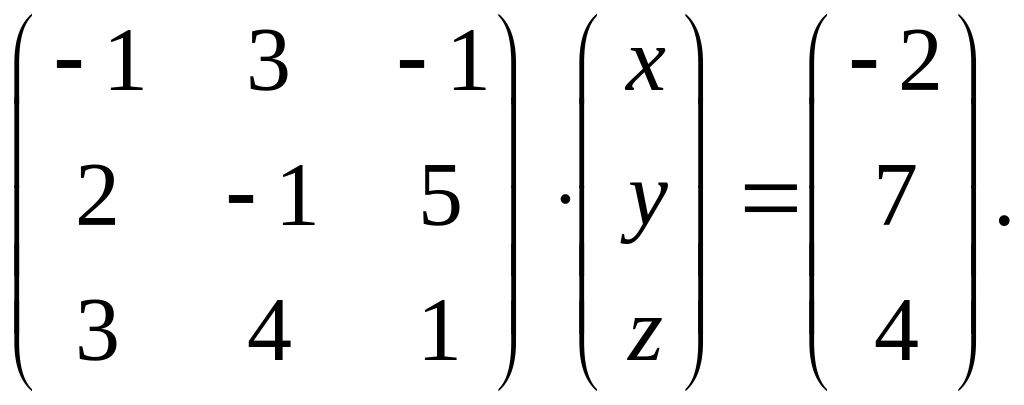
Вариант 6.
1.
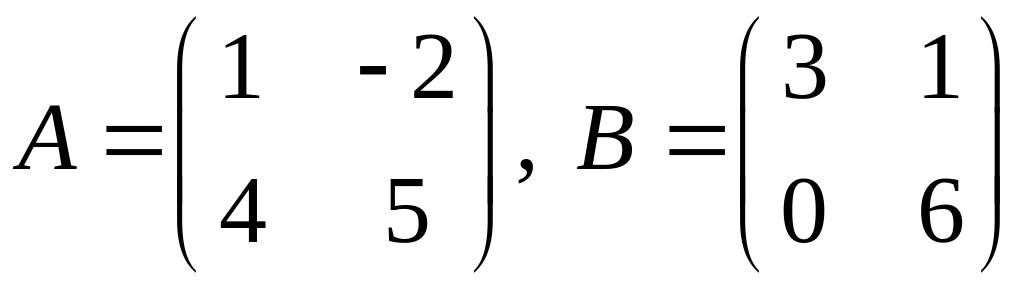 .
.
2.
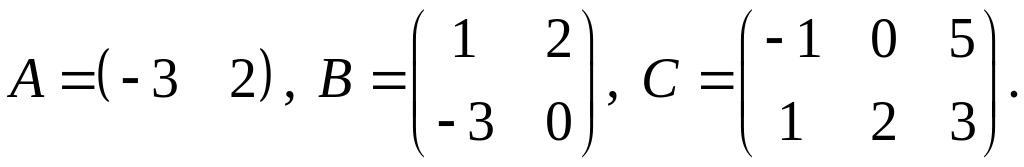
3.
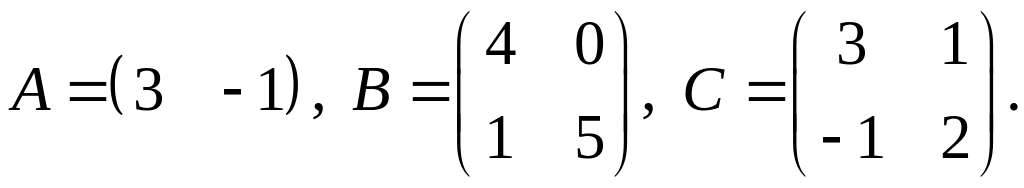
4.
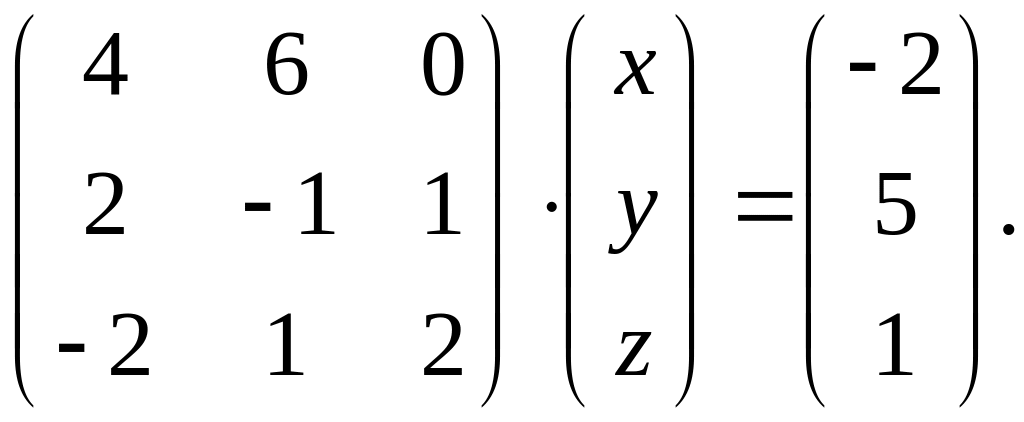
Вариант 7.
1.
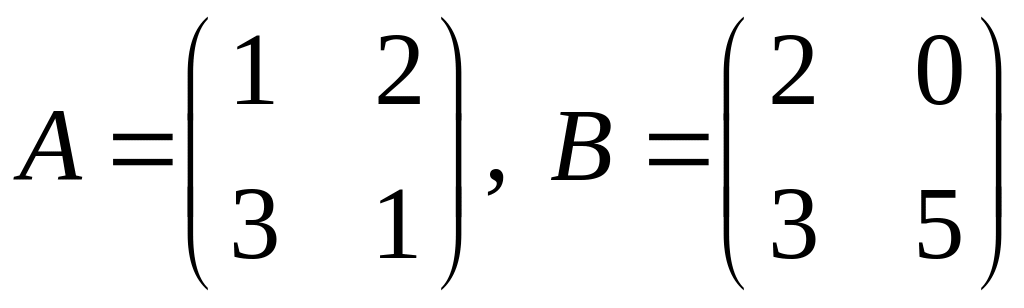 .
.
2.
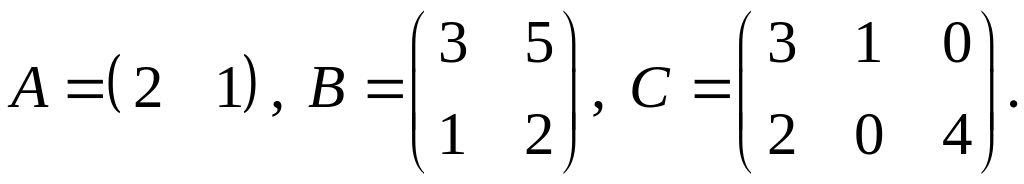
3.
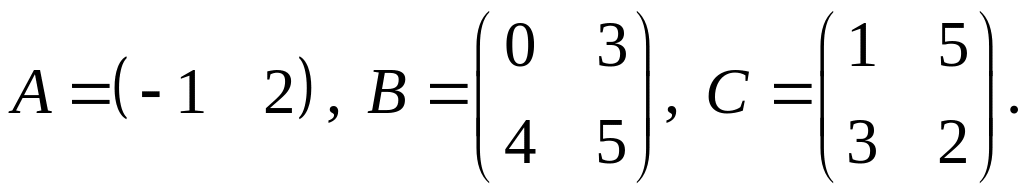
4.
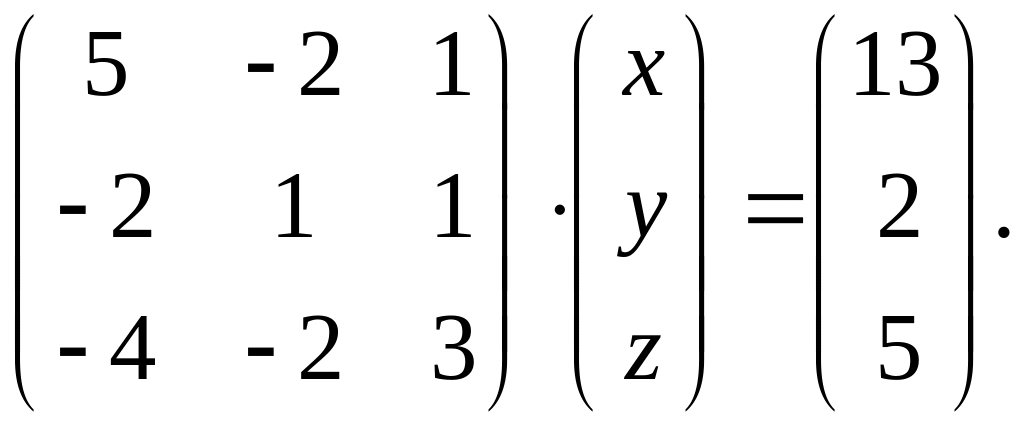
Вариант 8.
1.
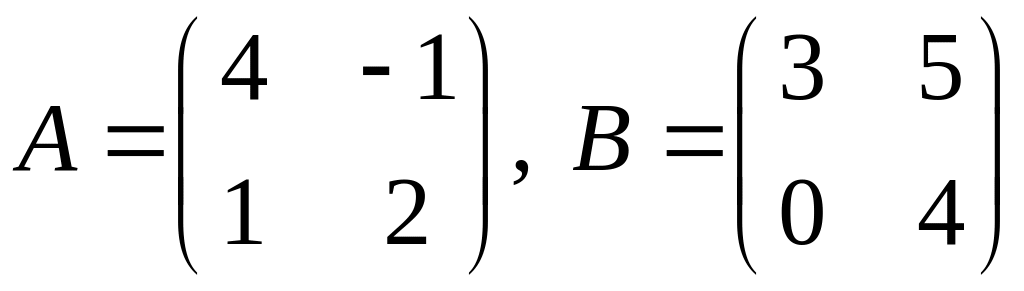 .
.
2.
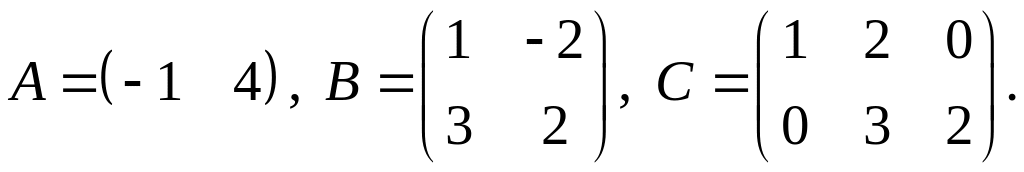
3.
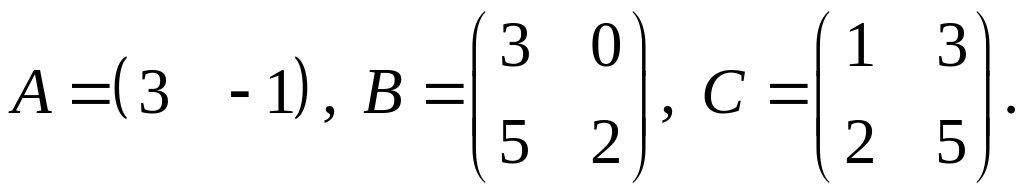
4.
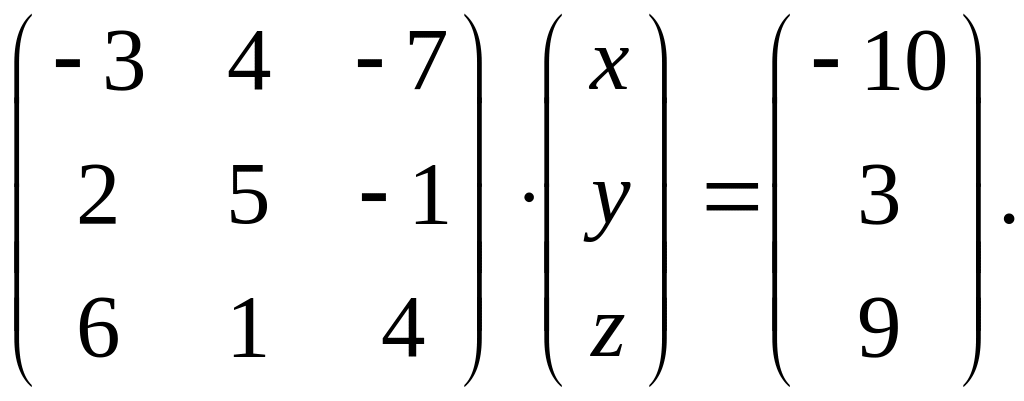
Вариант 9.
1.
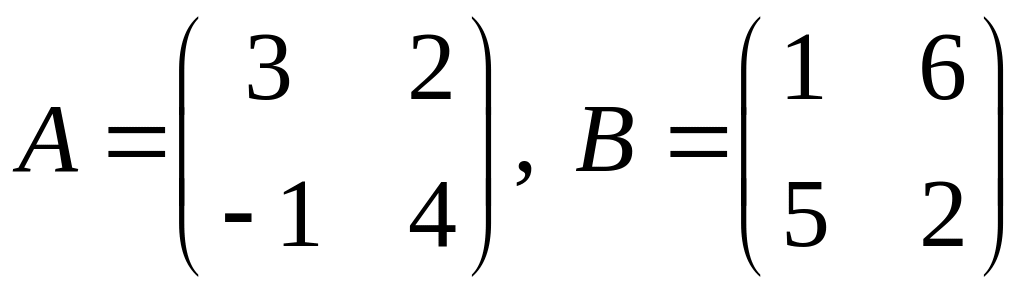 .
.
2.
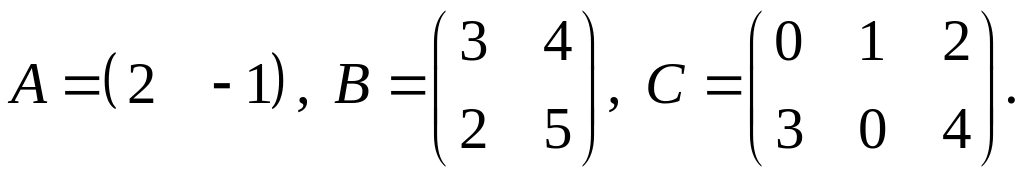
3.
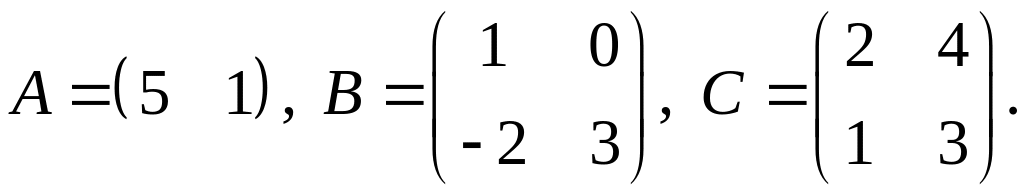
4.
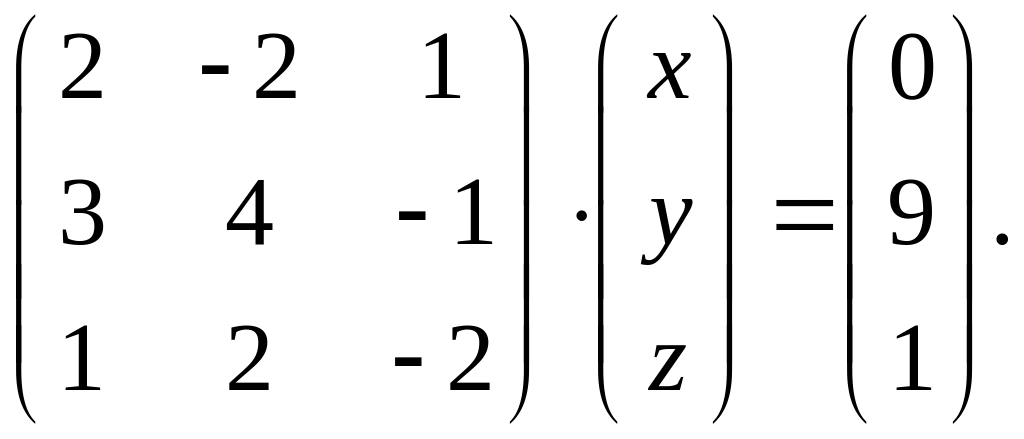
Вариант 10.
1.
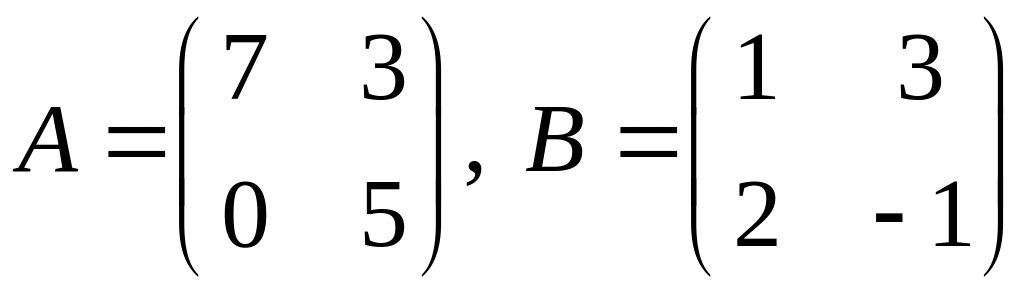 .
.
2.
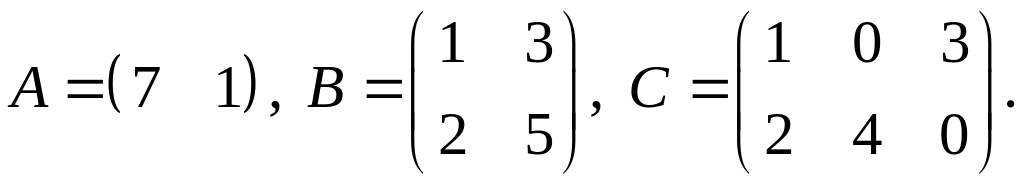
3.
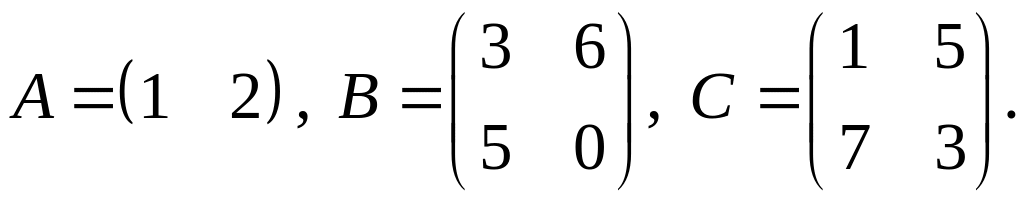
4.
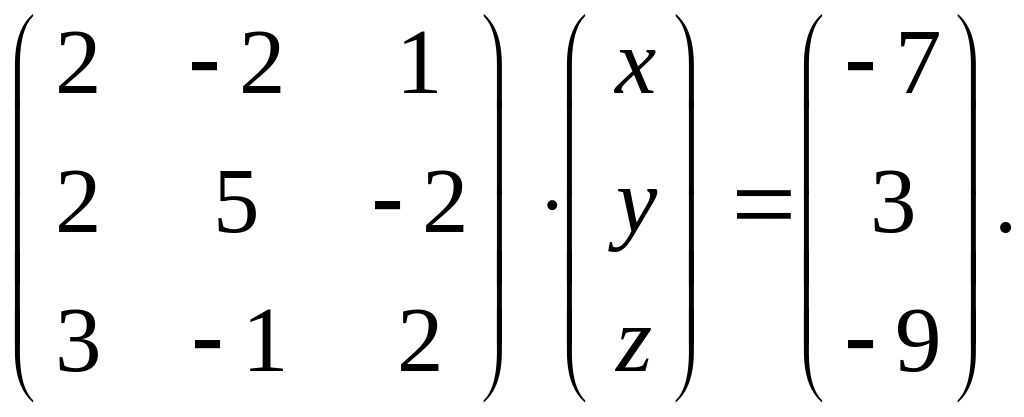
Вариант 11.
1.
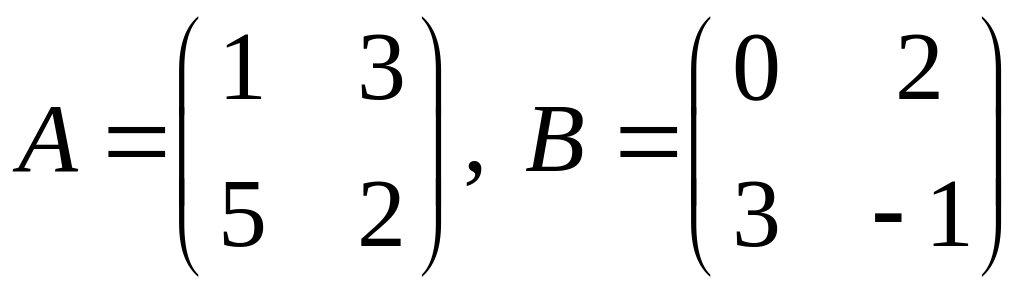 .
.
2.
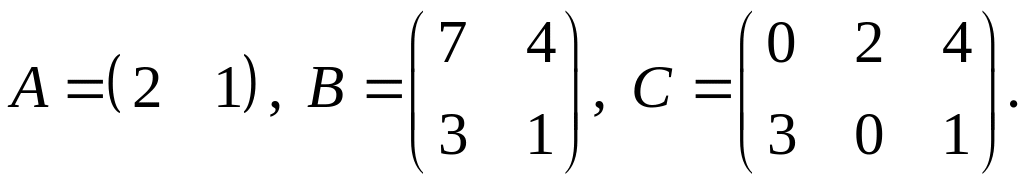
3.
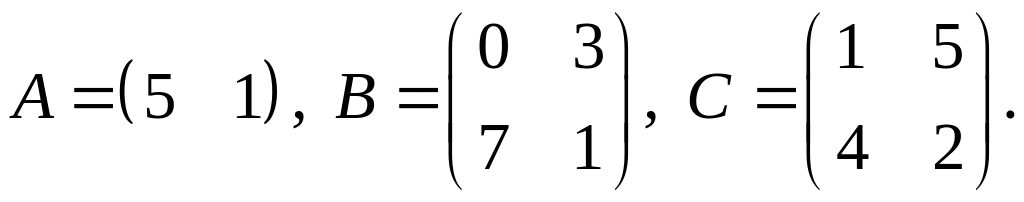
4.
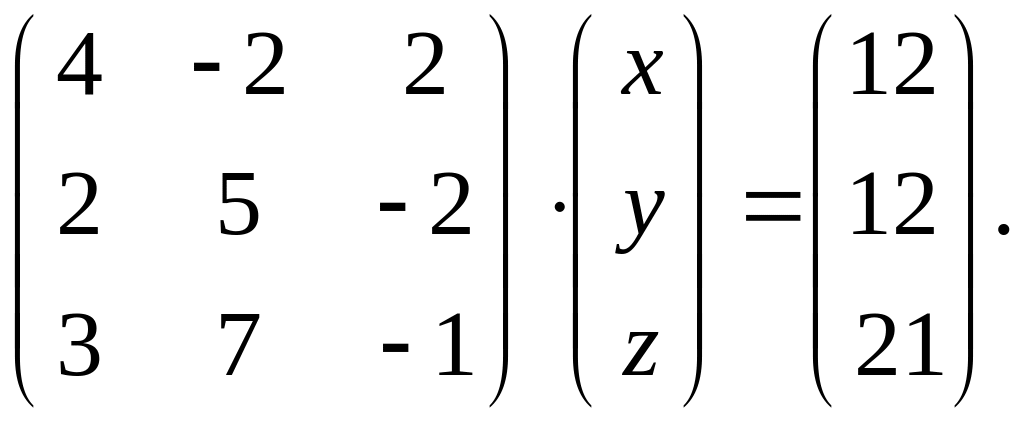
Вариант 12.
1.
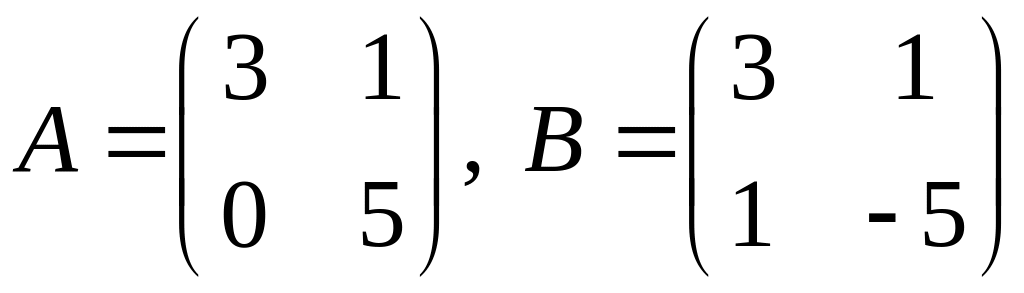 .
.
2.
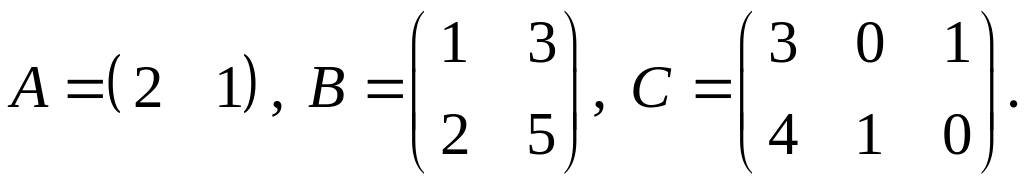
3.
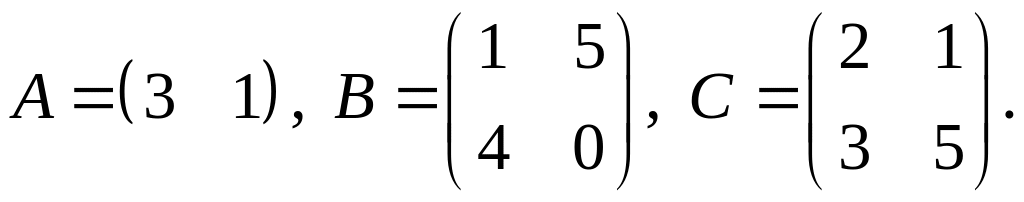
4.
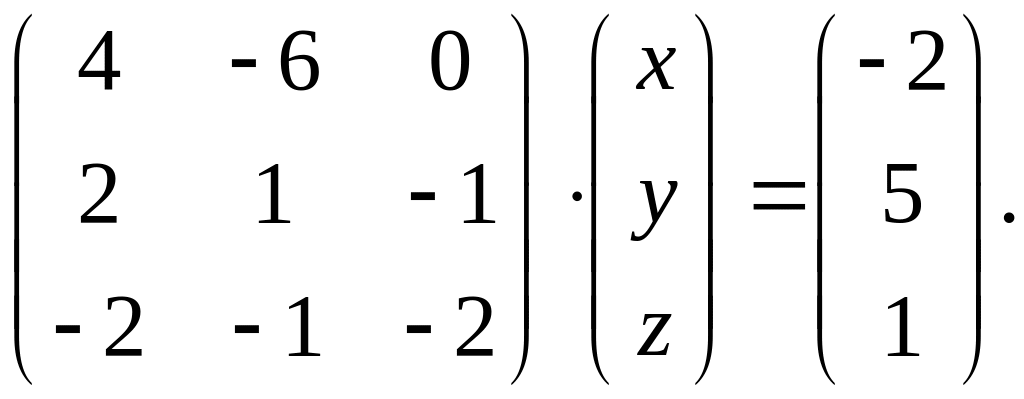
Вариант 13.
1.
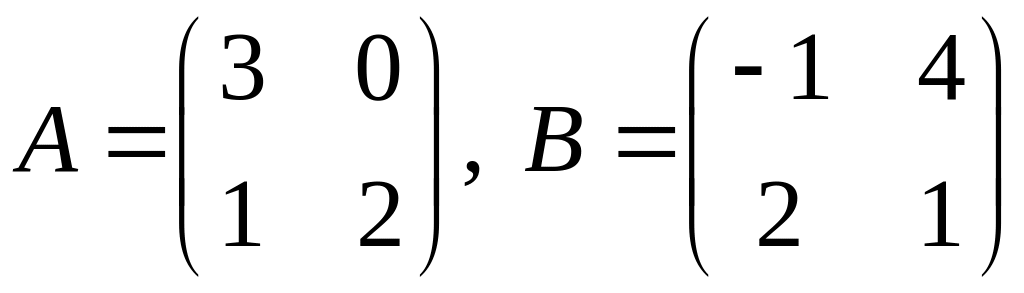 .
.
2.
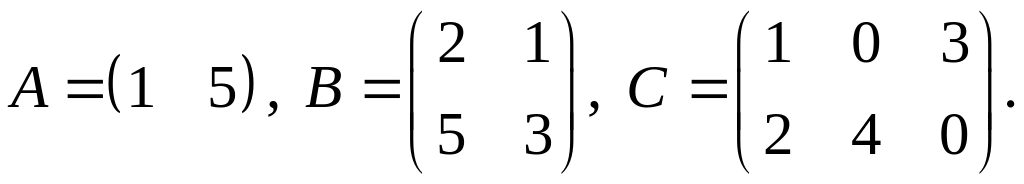
3.
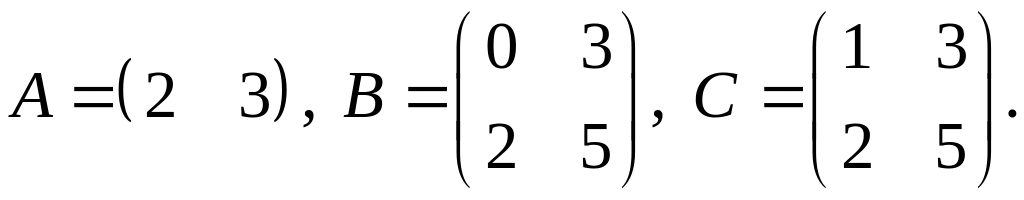
4.
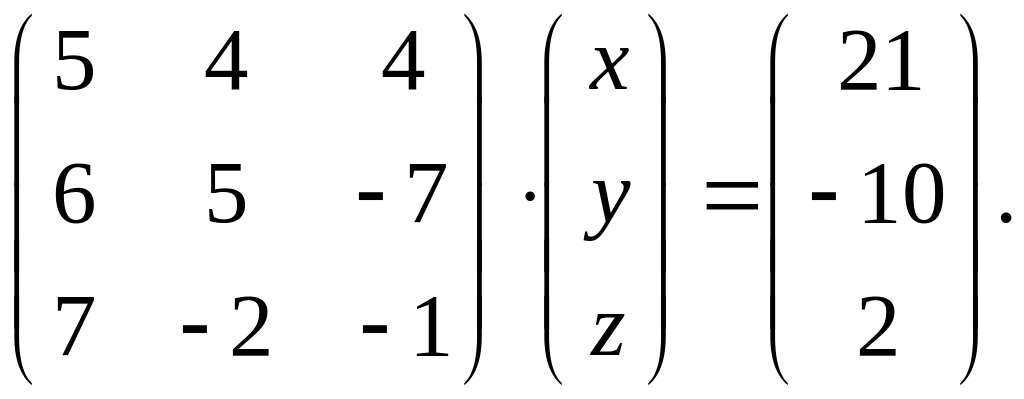
Вариант 14.
1.
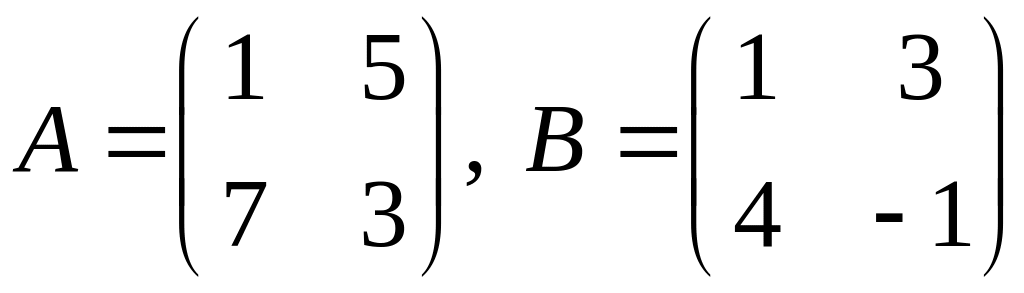 .
.
2.
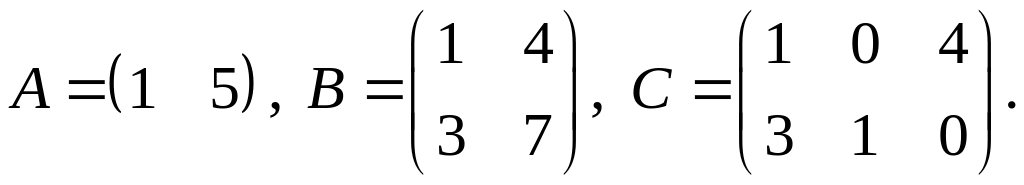
3.
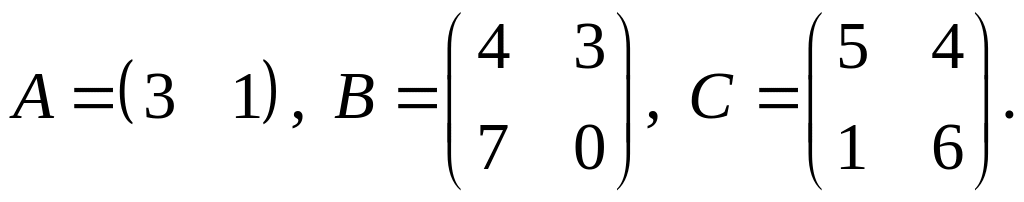
4.
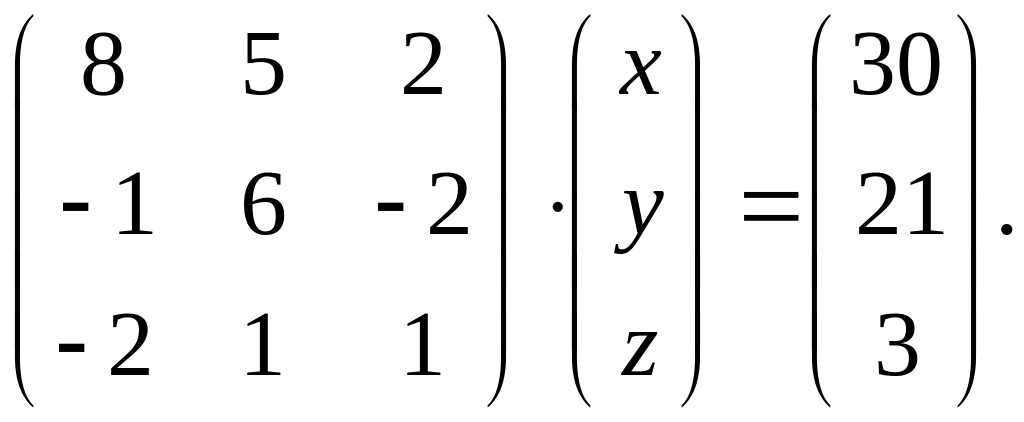
Вариант 15.
1.
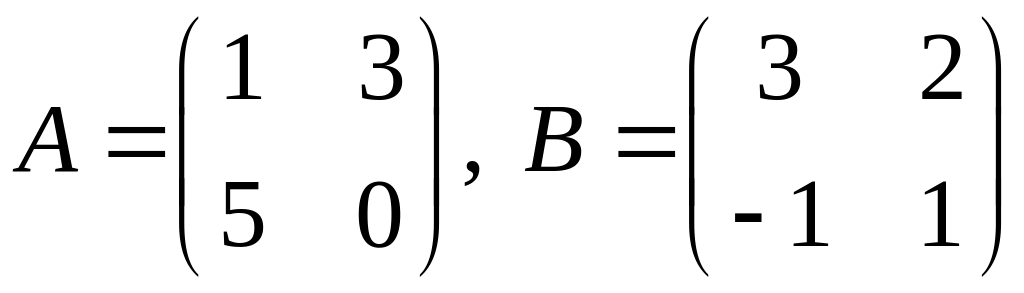 .
.
2.
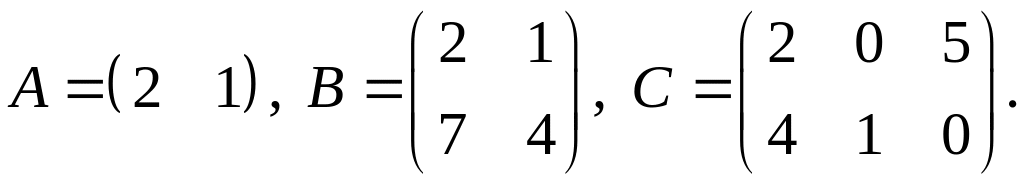
3.
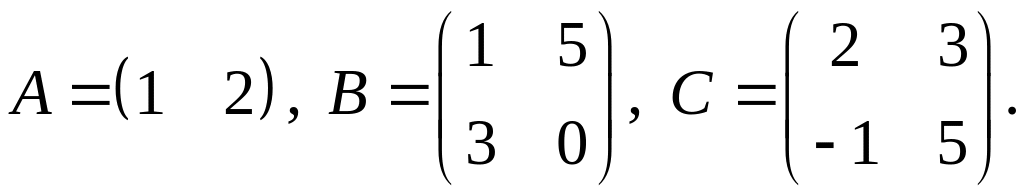
4.
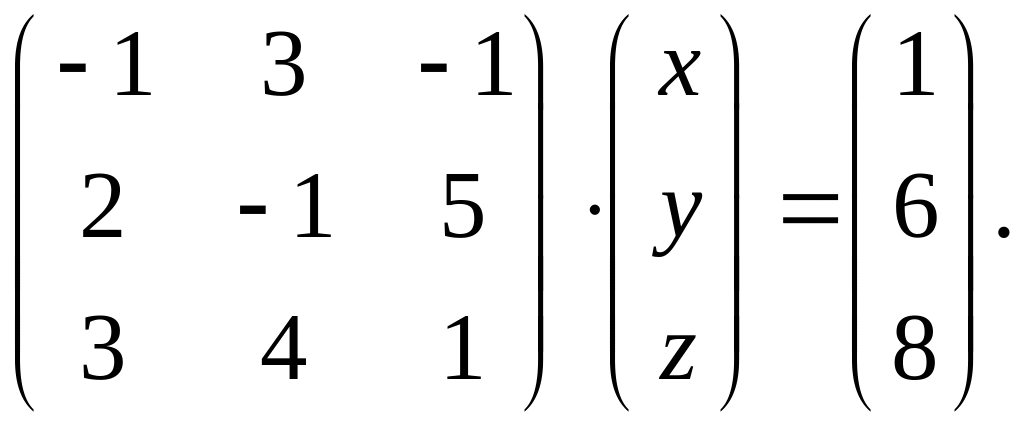
Вариант 16.
1.
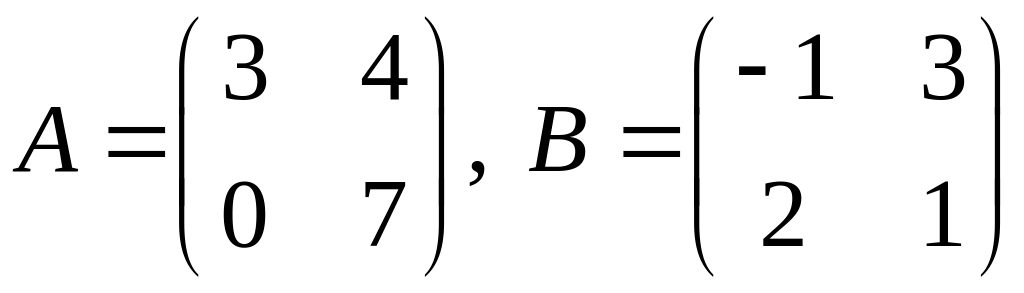 .
.
2.
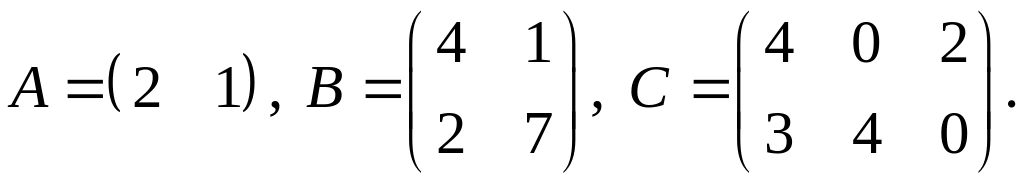
3.
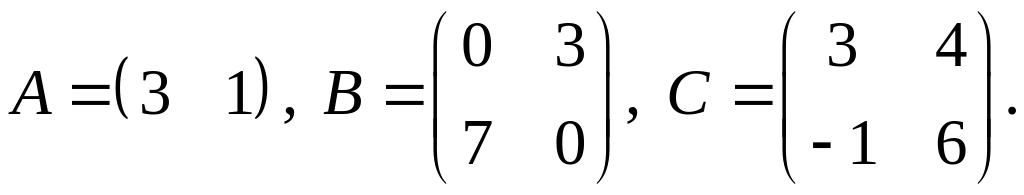
4.
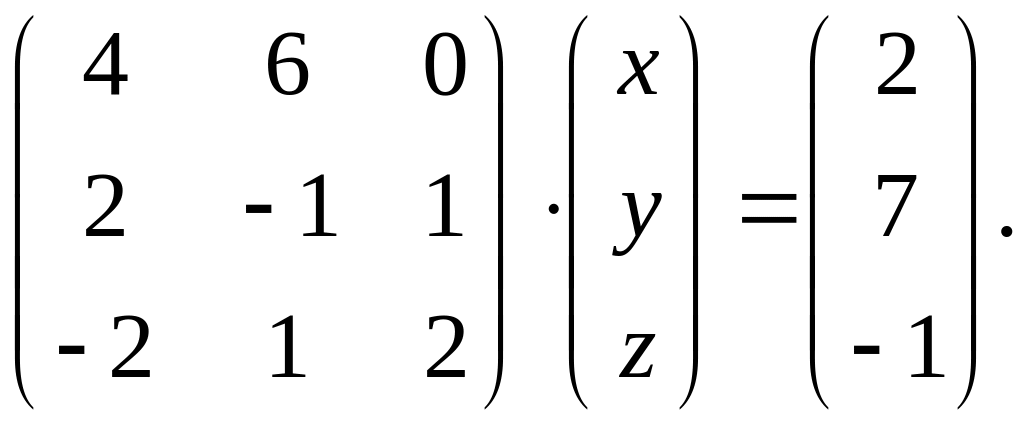
Вариант 17.
1.
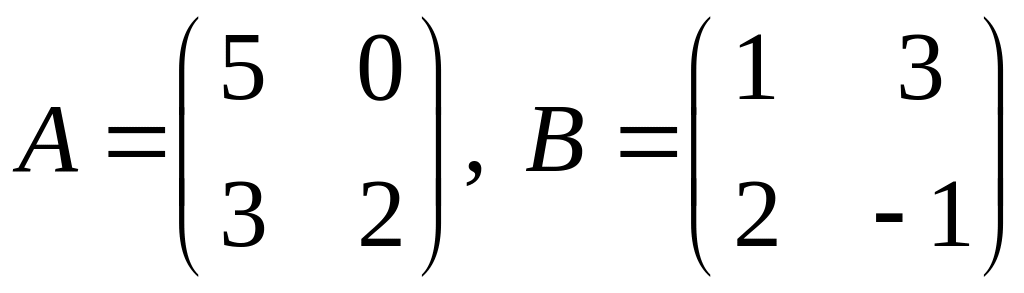 .
.
2.
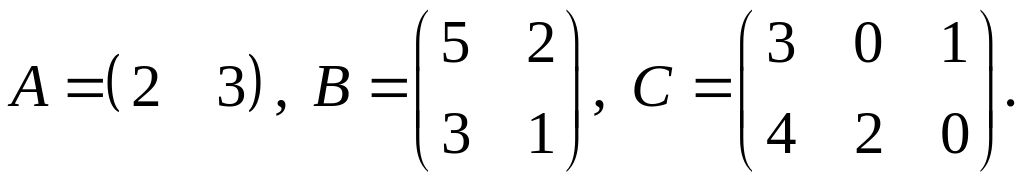
3.
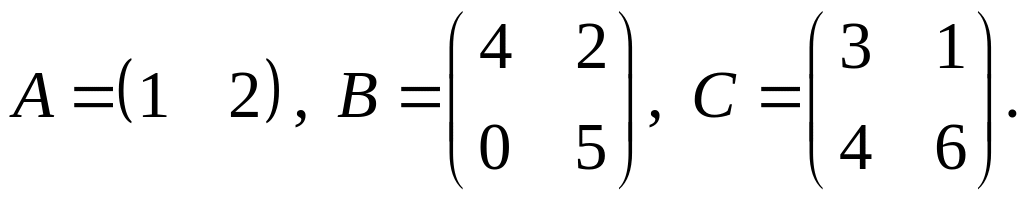
4.
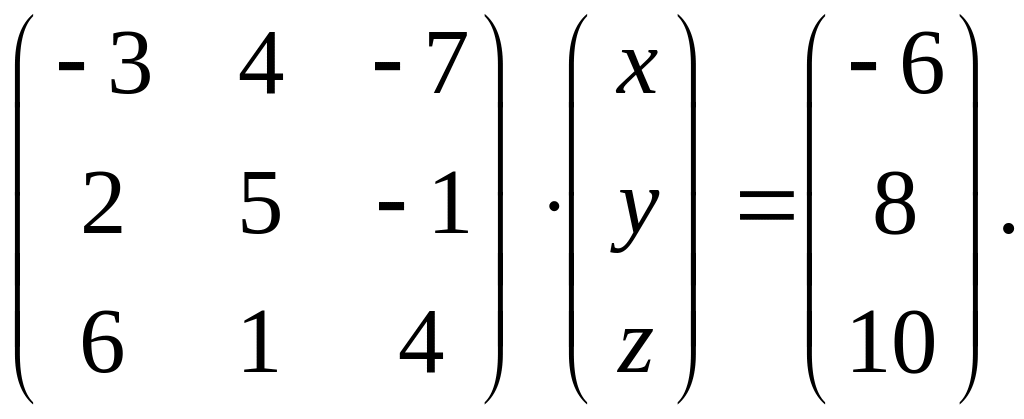
Вариант 18.
1.
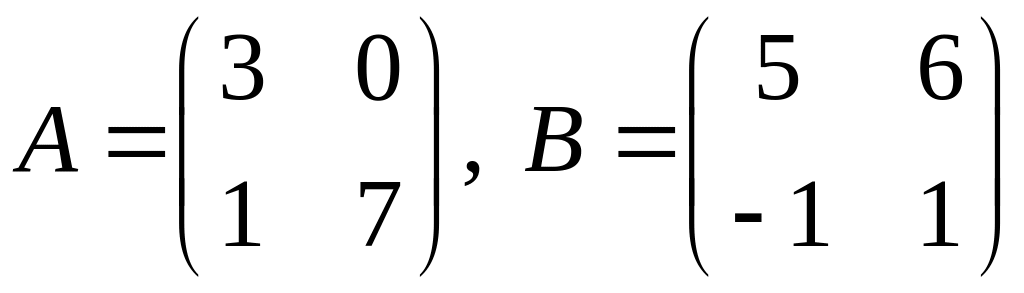 .
.
2.
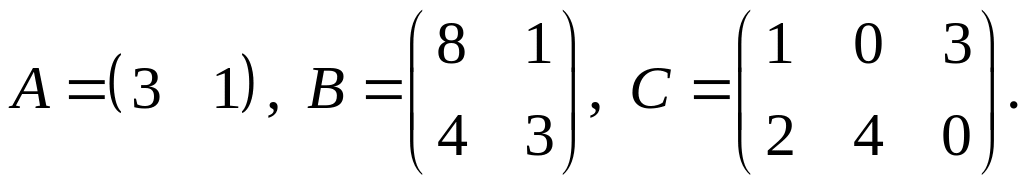
3.
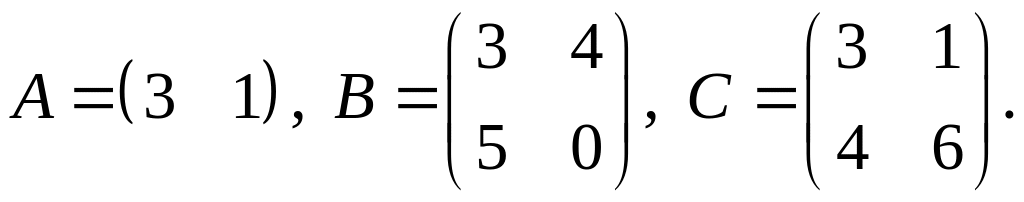
4.
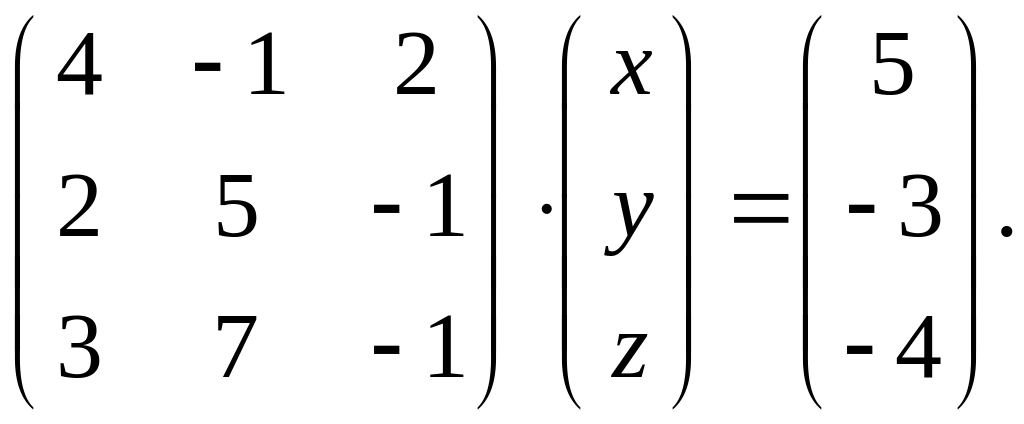
Вариант 19.
1.
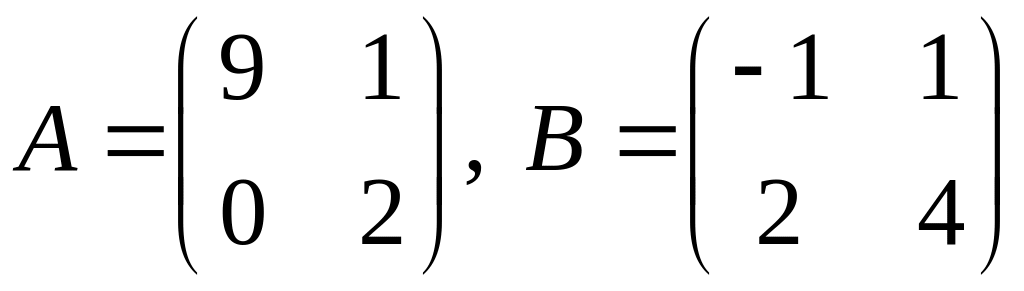 .
.
2.
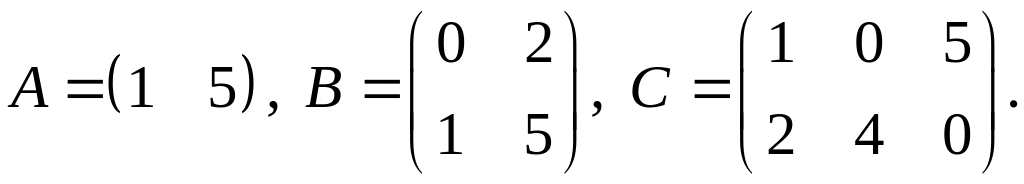
3.
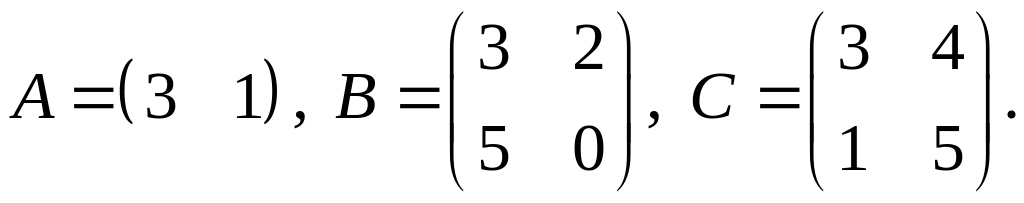
4.
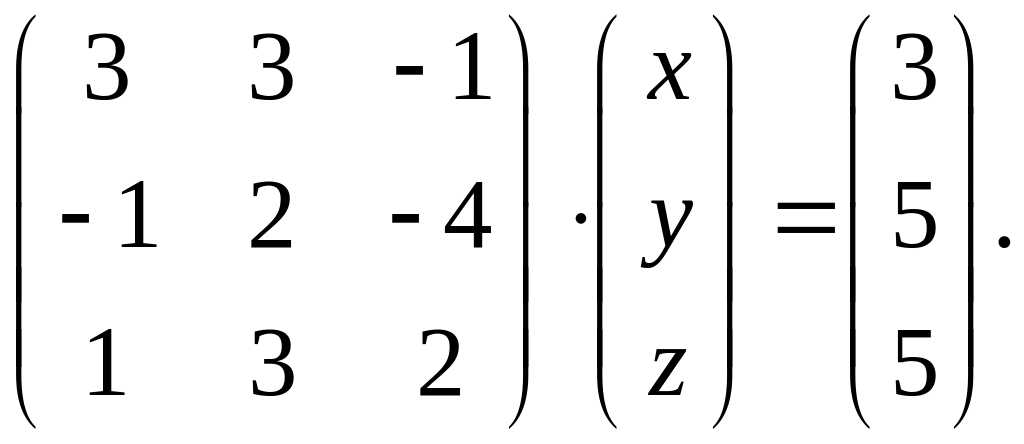
Вариант 20.
1.
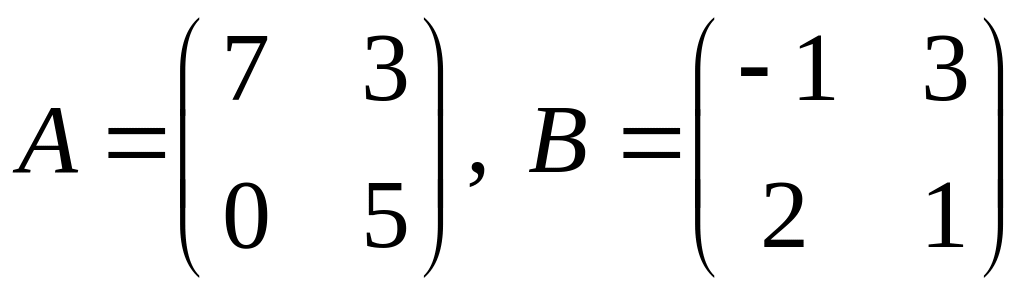 .
.
2.
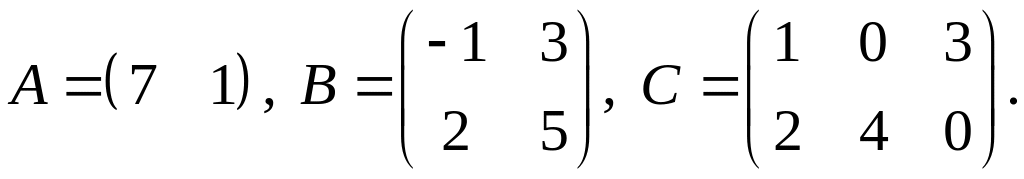
3.
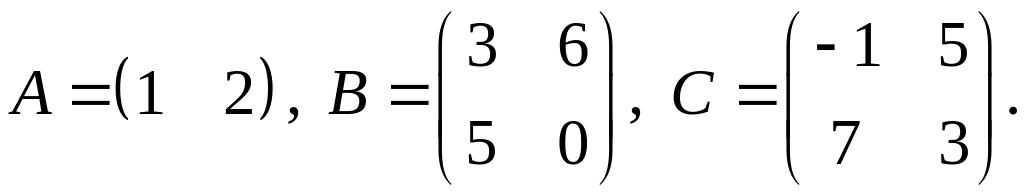
4.
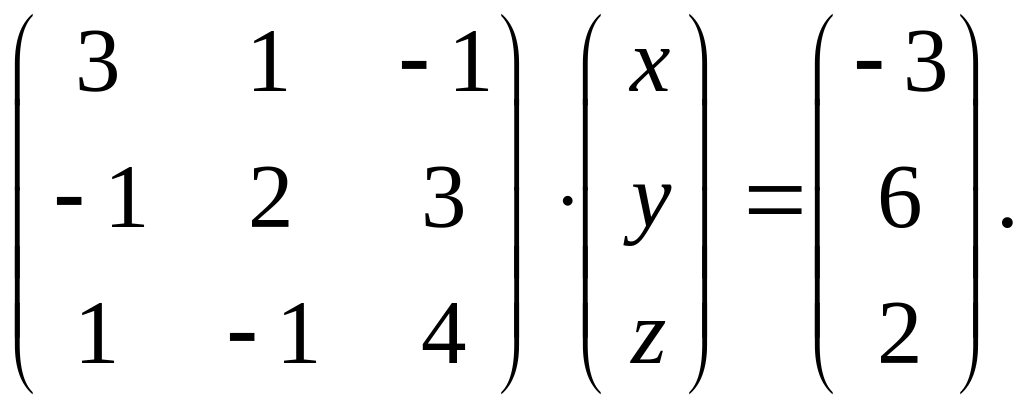
Вариант 21.
1.
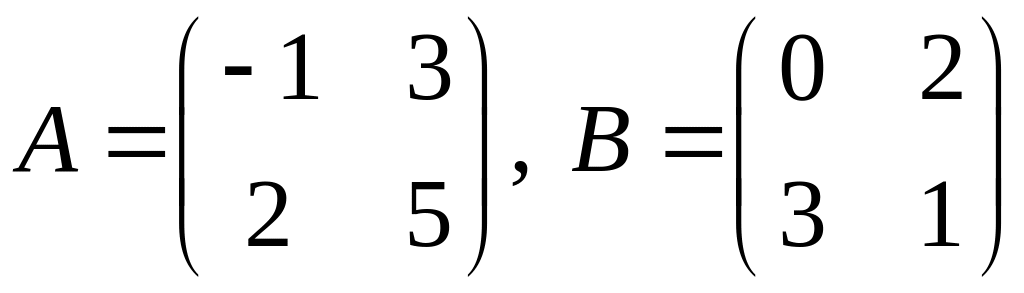 .
.
2.
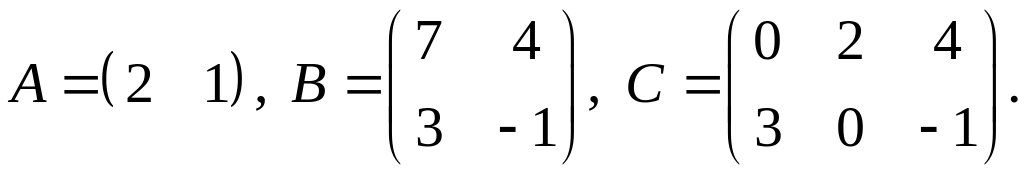
3.
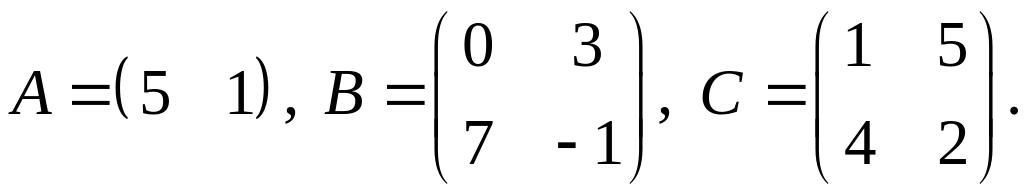
4.
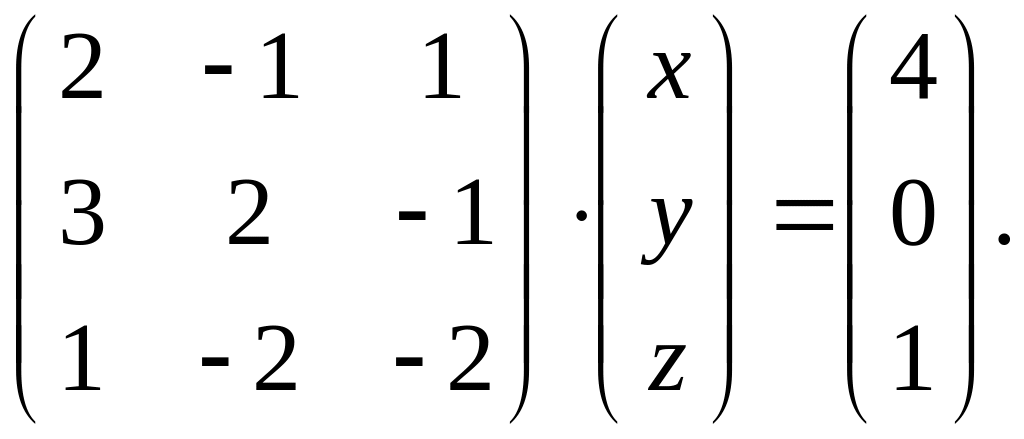
Вариант 22.
1.
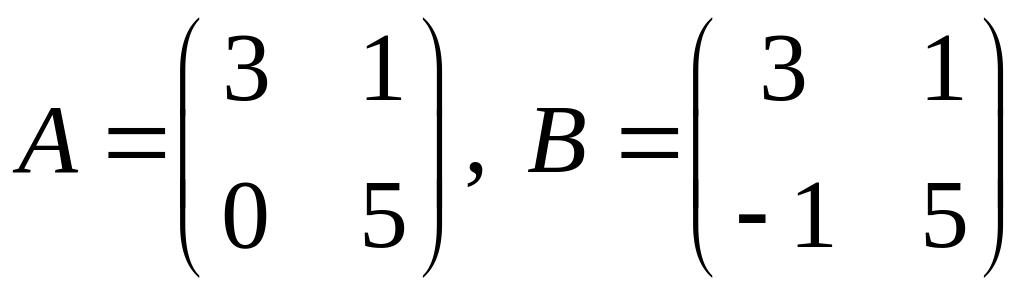 .
.
2.
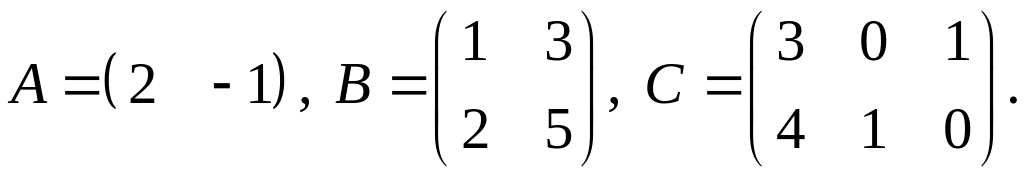
3.
4.
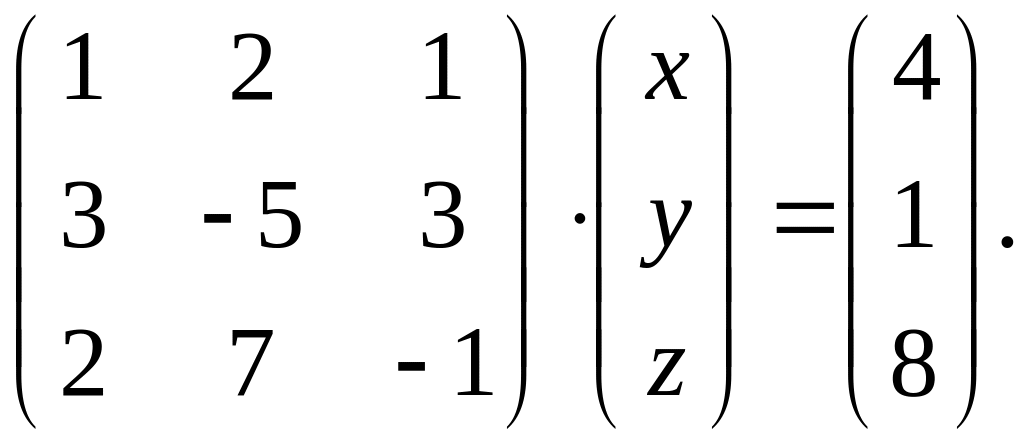
Вариант 23.
1.
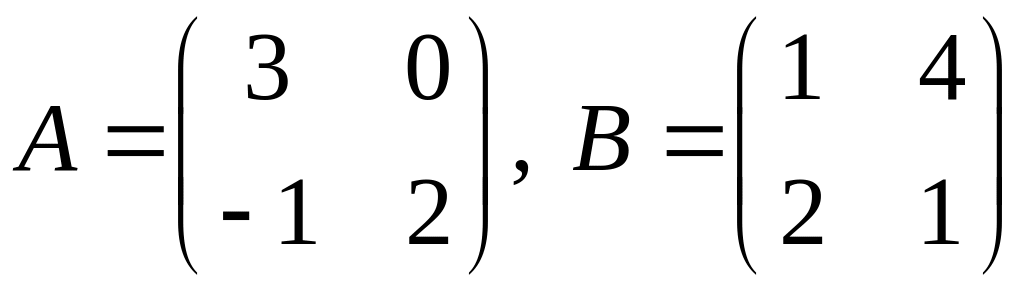 .
.
2.
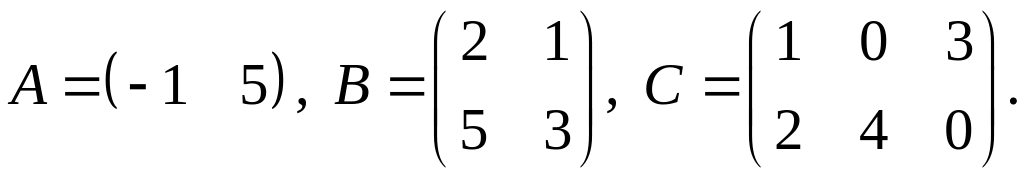
3.
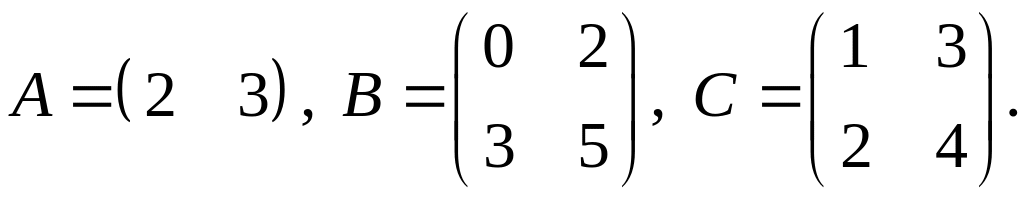
4.
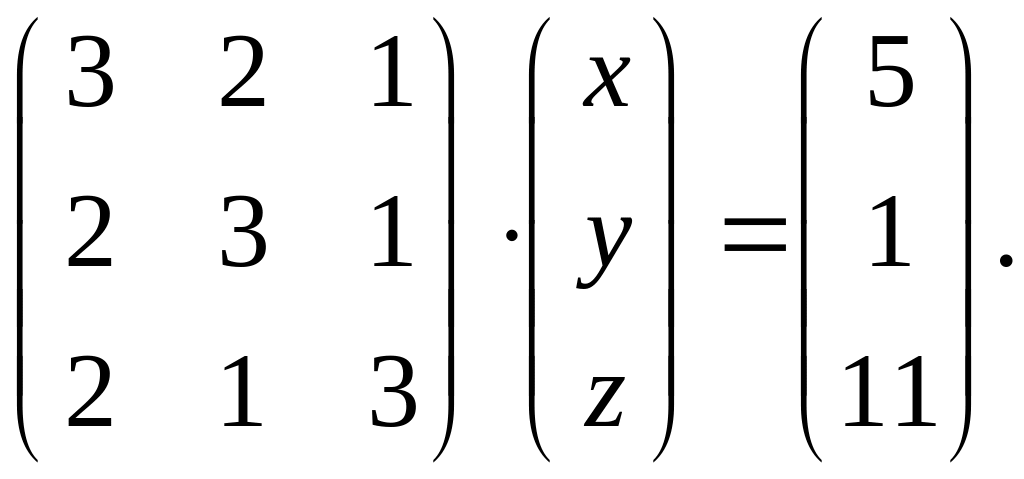
Вариант 24.
1.
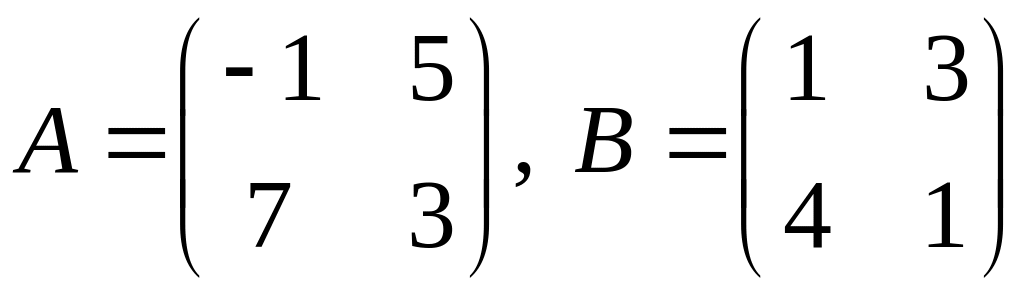 .
.
2.
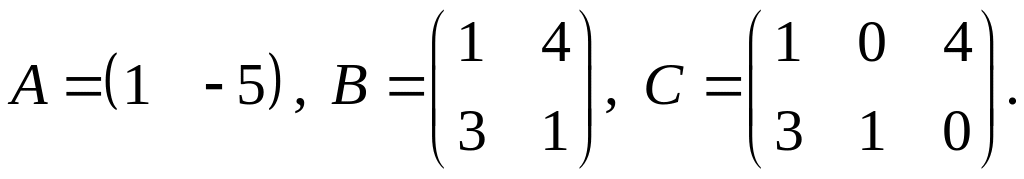
3.
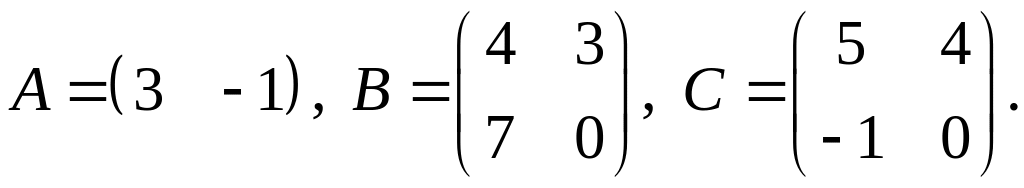
4.
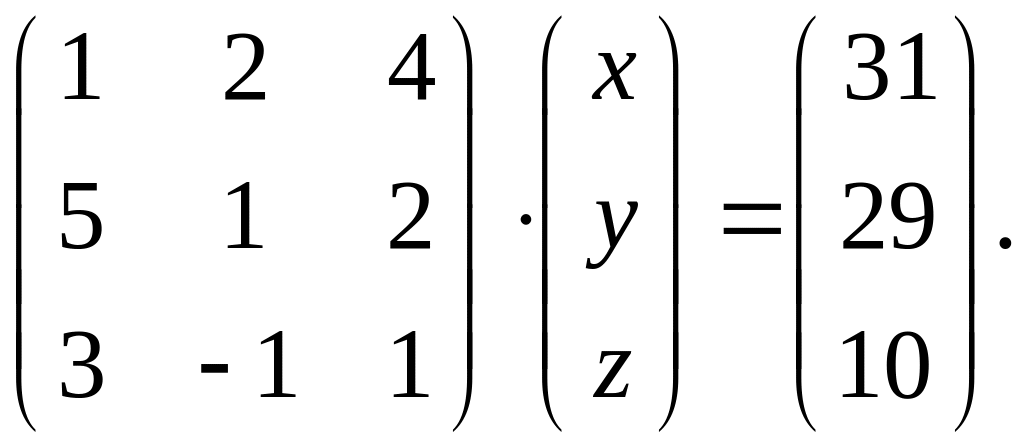
Вариант 25.
1.
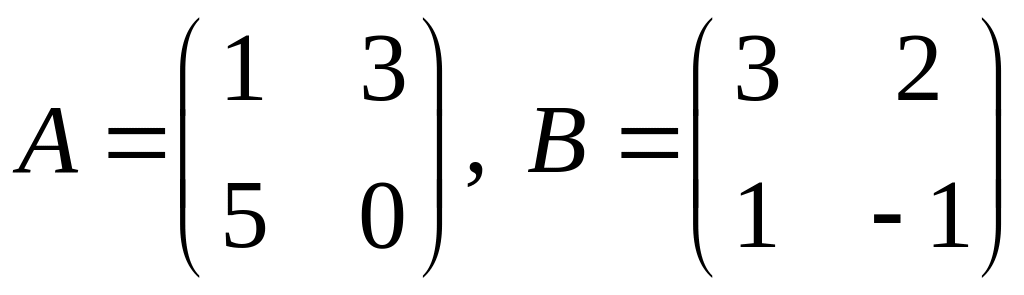 .
.
2.
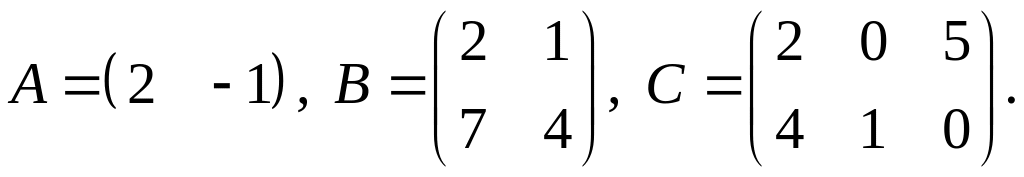
3.
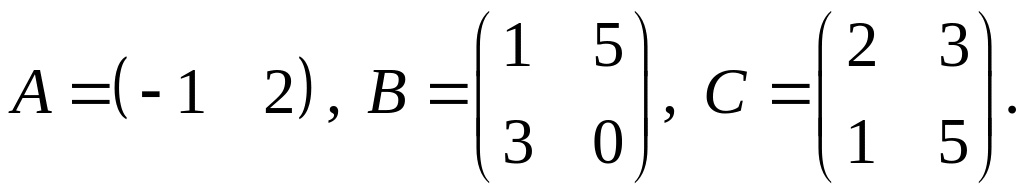
4.
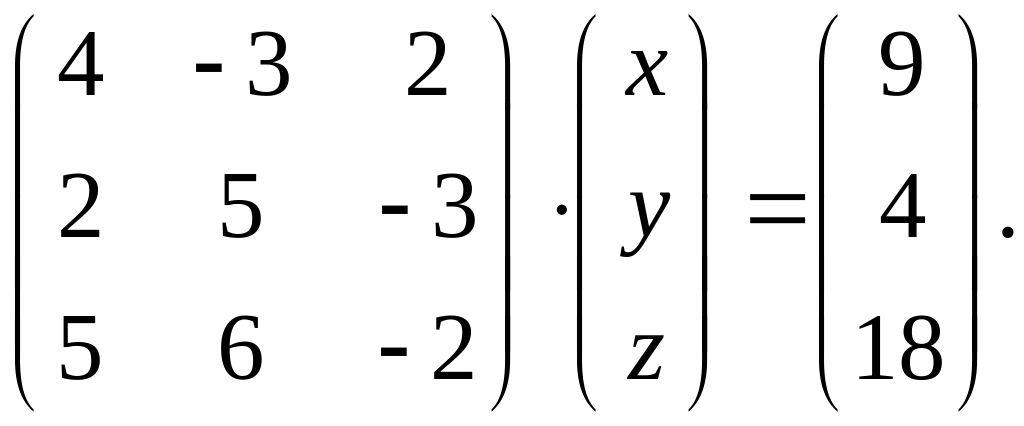
Вариант 26.
1.
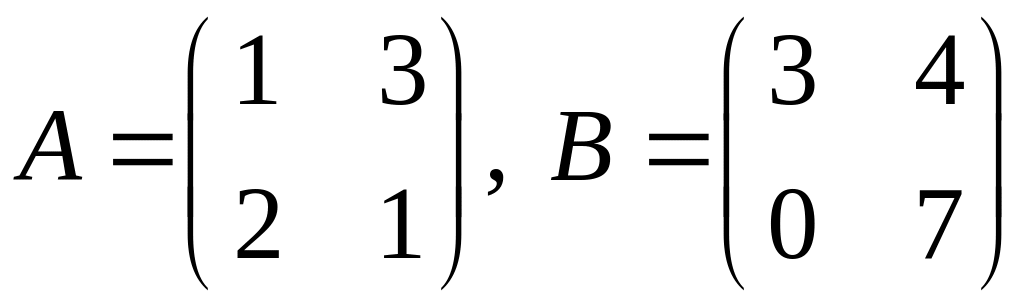 .
.
2.
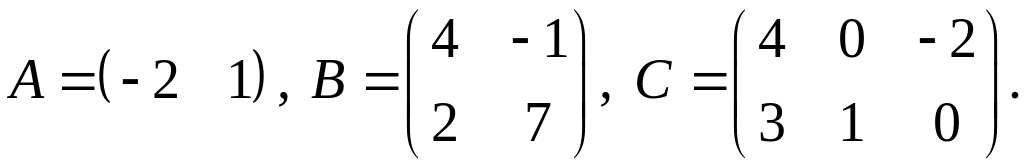
3.
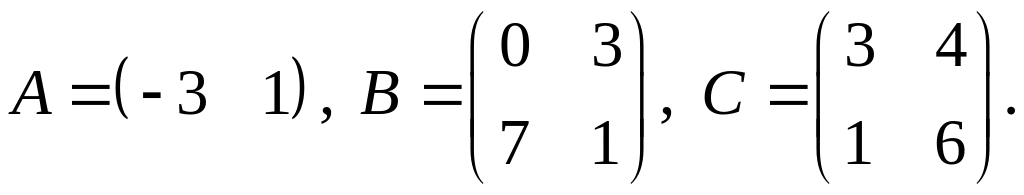
4.
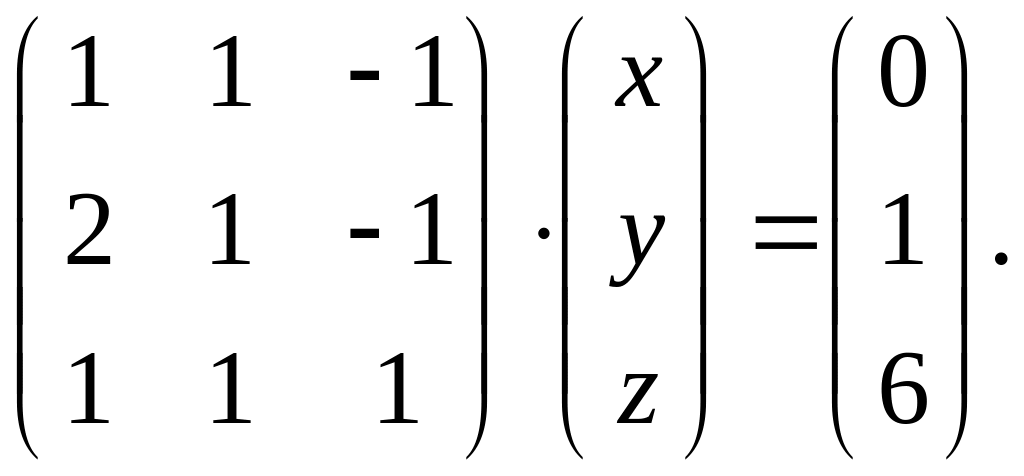
Вариант 27.
1.
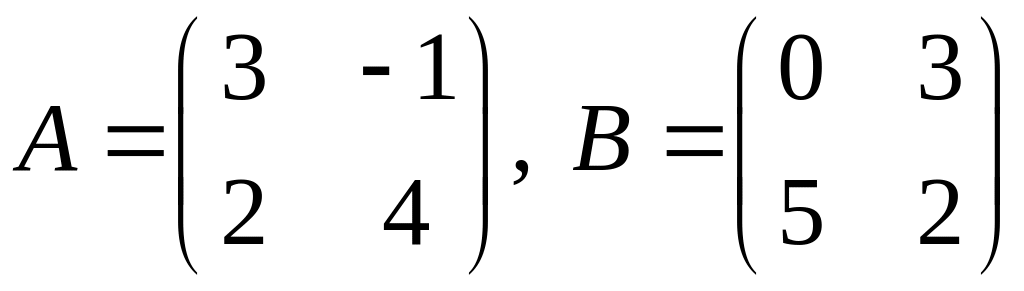 .
.
2.
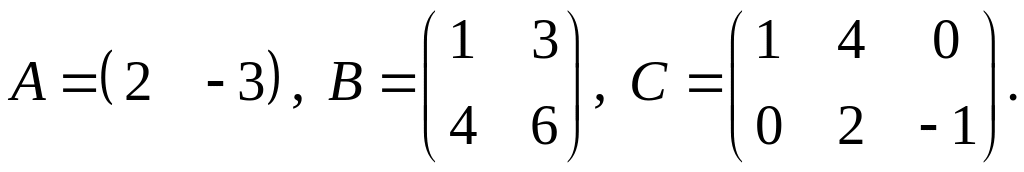
3.
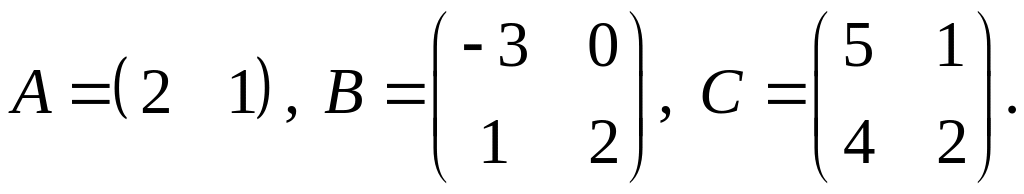
4.
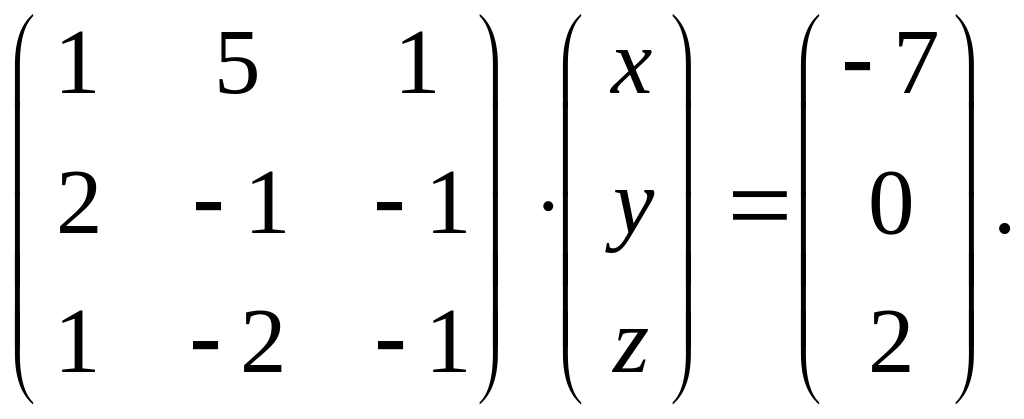
Вариант 28.
1.
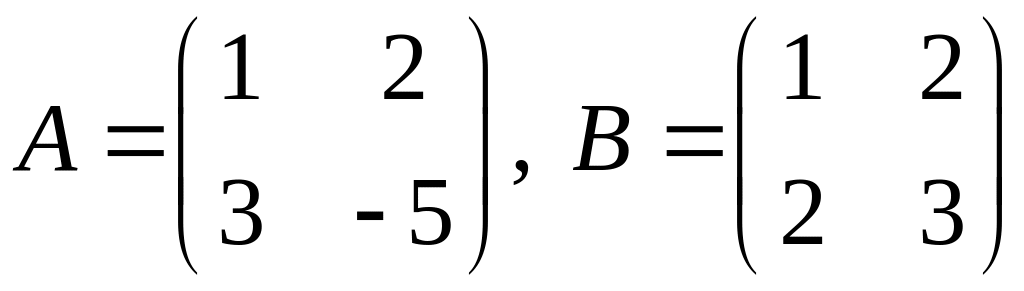 .
.
2.
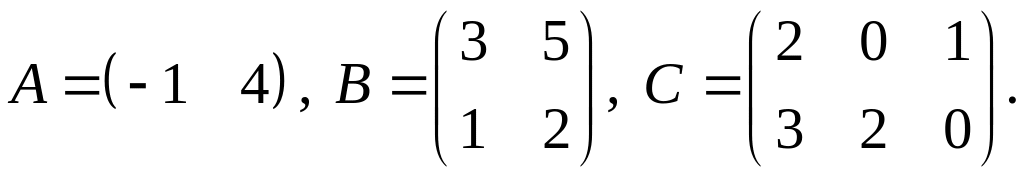
3.
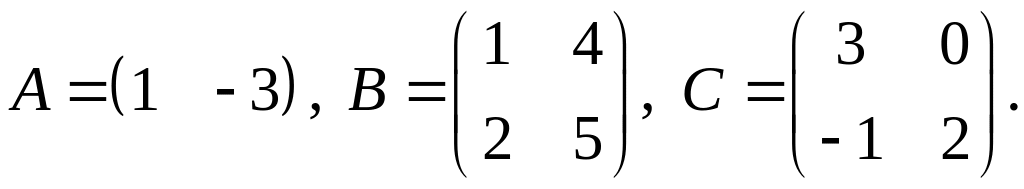
4.
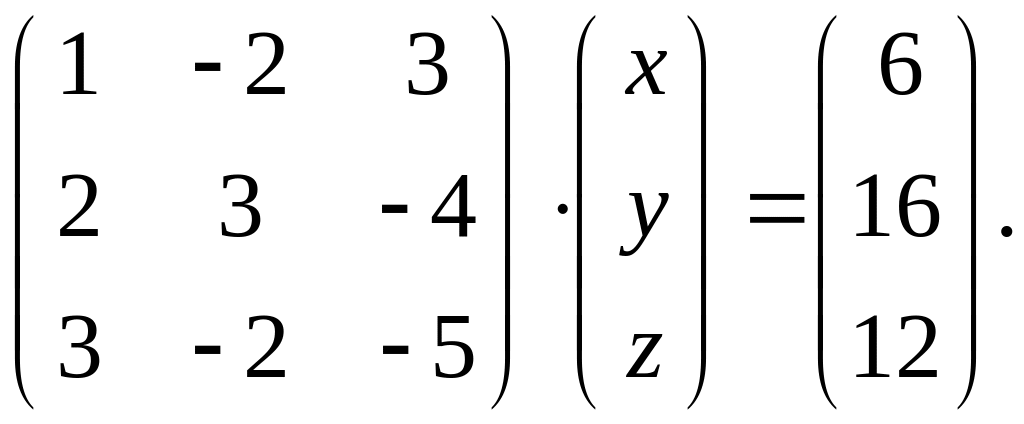
РЕШЕНИЕ ТИПОВОГО ЗАДАНИЯ
1. Проверить, справедливо ли равенство , если
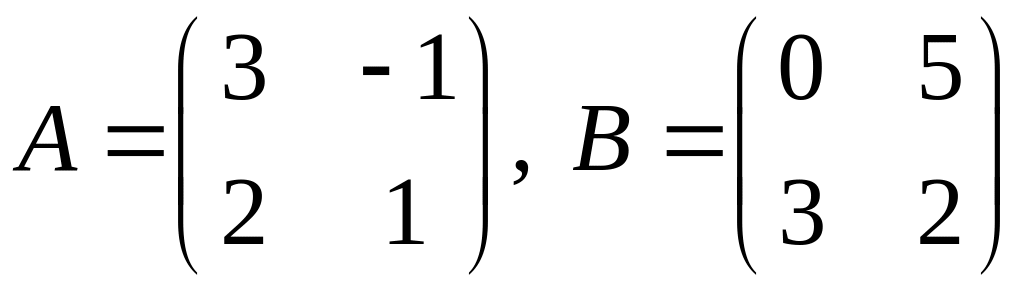 .
.
Решение.
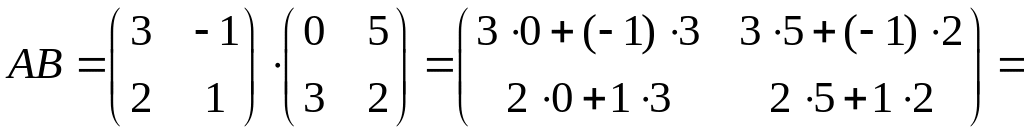
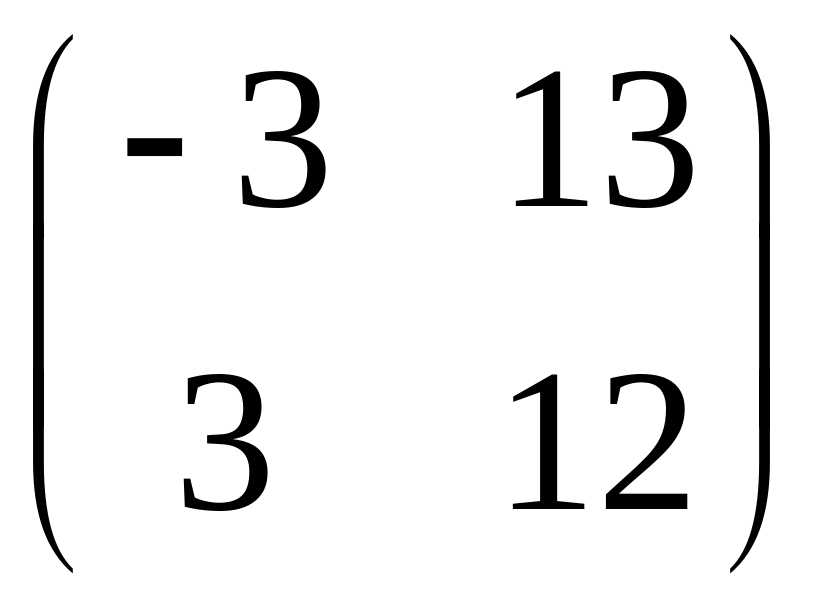 .
.
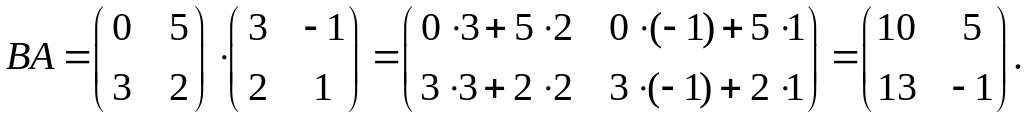
Вывод:
![]()
2. Даны матрицы
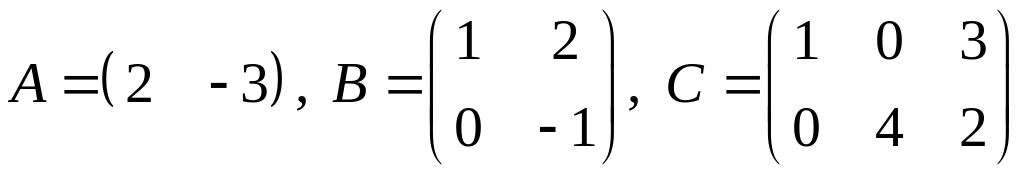 .
Показать непосредственным вычислением,
что
.
.
Показать непосредственным вычислением,
что
.
Решение.
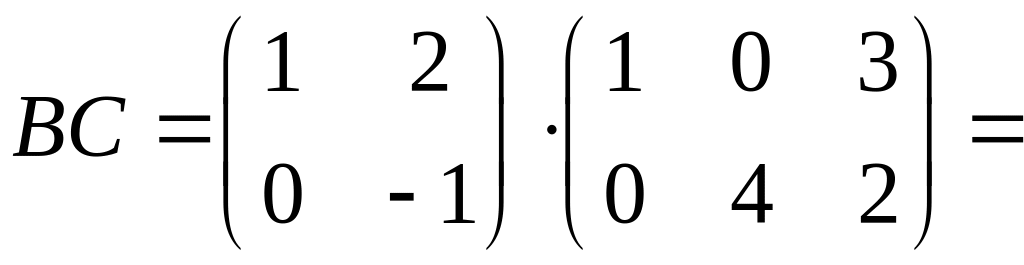
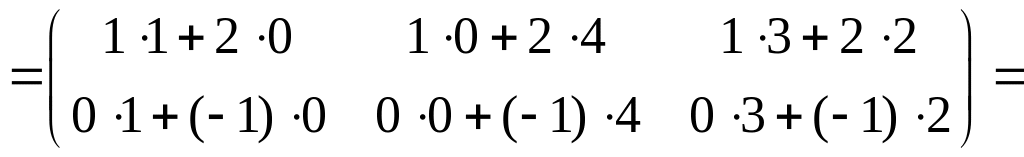
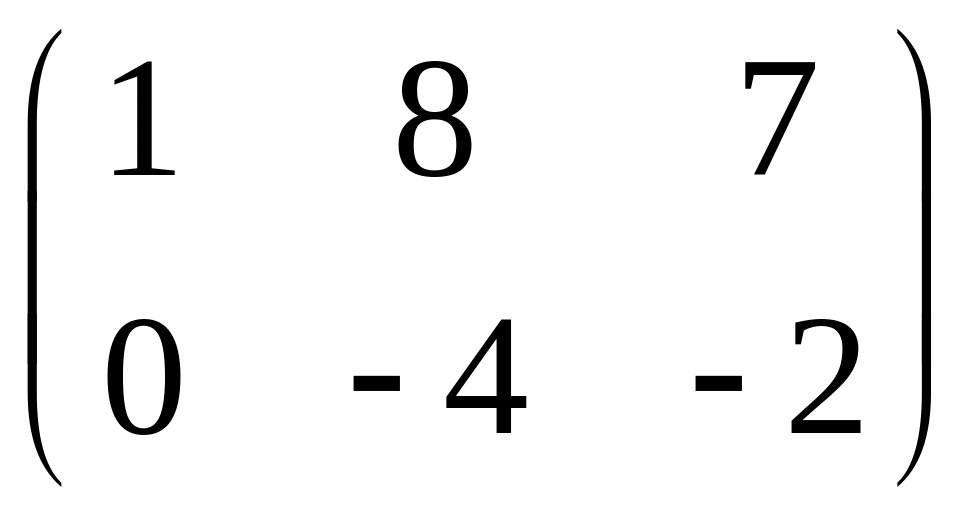 ;
;
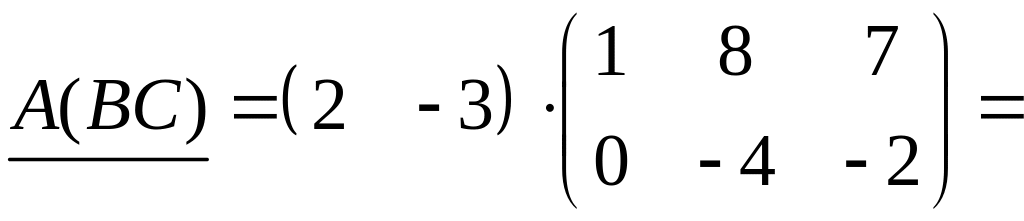
![]()
![]() .
.

![]() ;
;
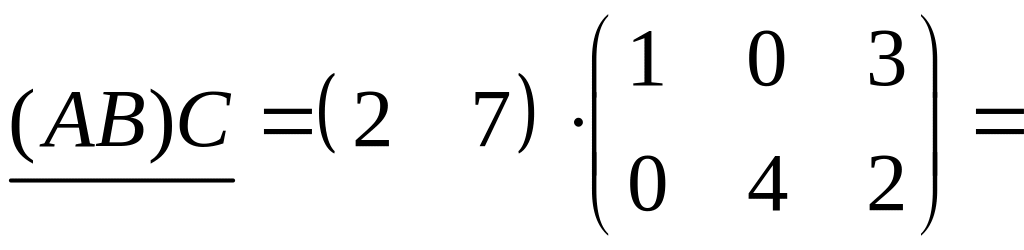
![]() .
.
Итак,
![]() .
.
3. Даны матрицы
![]() ,
,
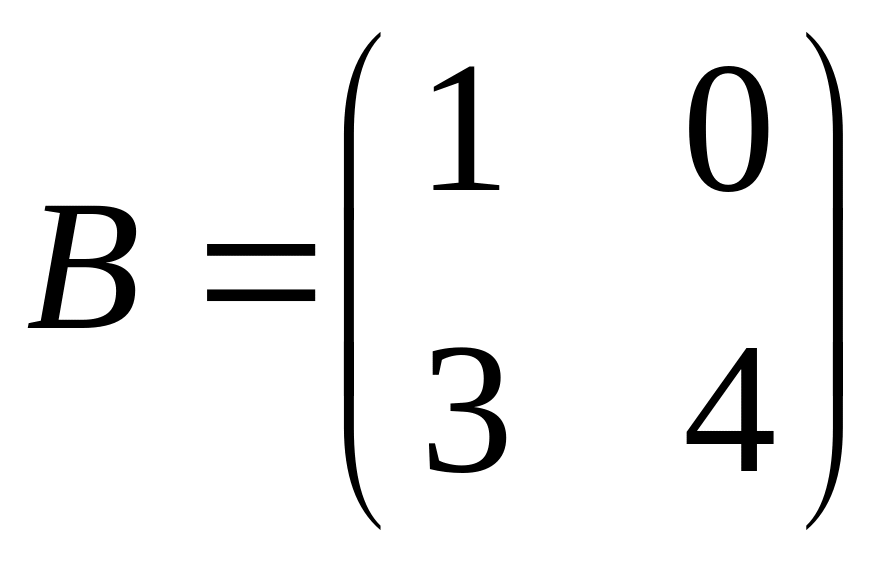 ,
,
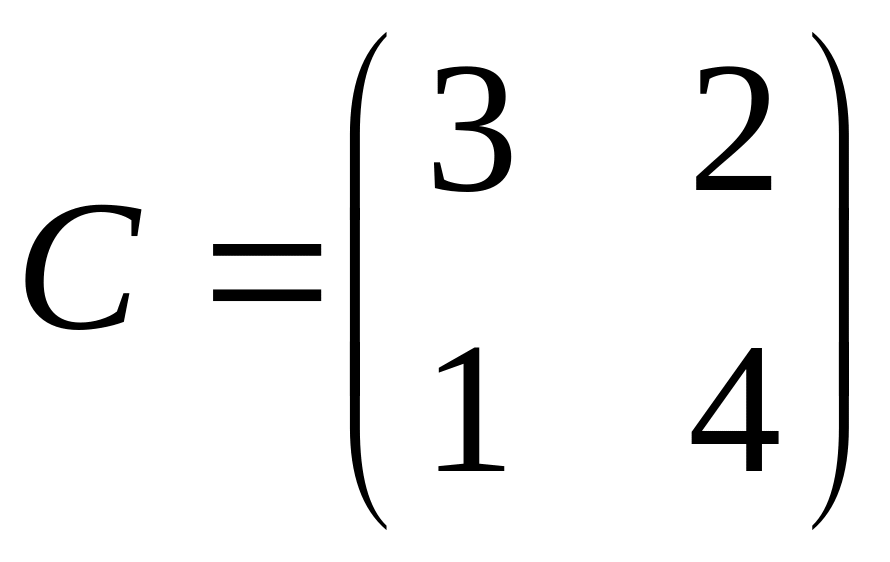 .
Показать непосредственным вычислением,
что
.
.
Показать непосредственным вычислением,
что
.
Решение.
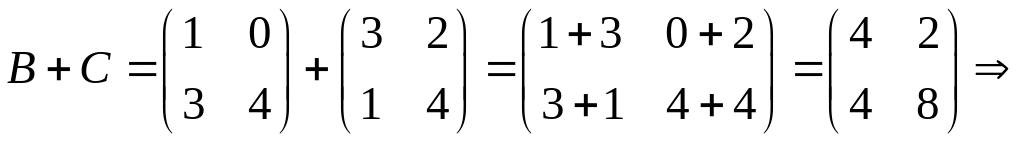
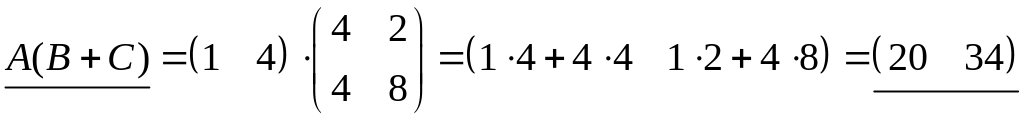 .
.
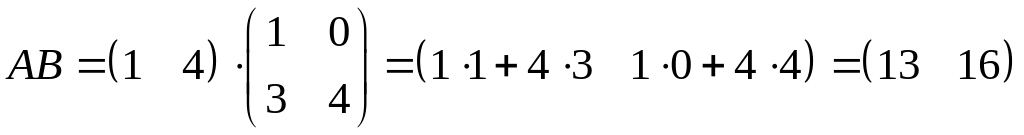 ;
;
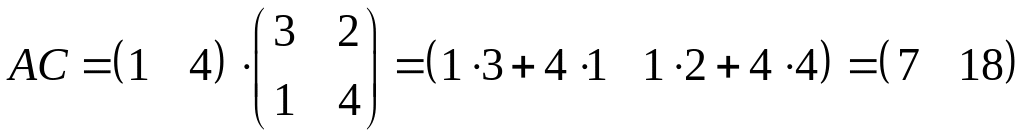
![]() .
.
Итак,
![]() .
.
4. Требуется записать матричное равенство
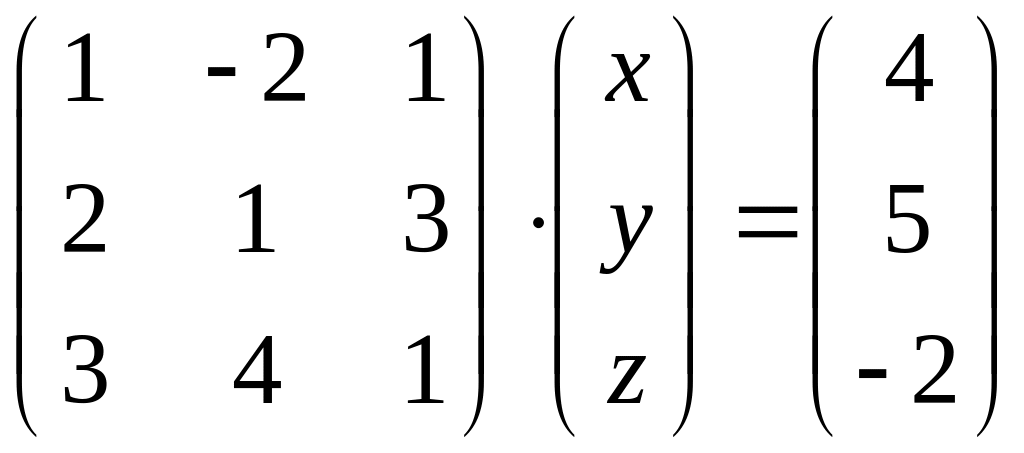
как систему уравнений с неизвестными и решить ее а) с помощью формул Крамера; б) методом Гаусса последовательного исключения неизвестных.
Решение. Перемножая матрицы левой части равенства и учитывая матрицу из его правой части, получаем:
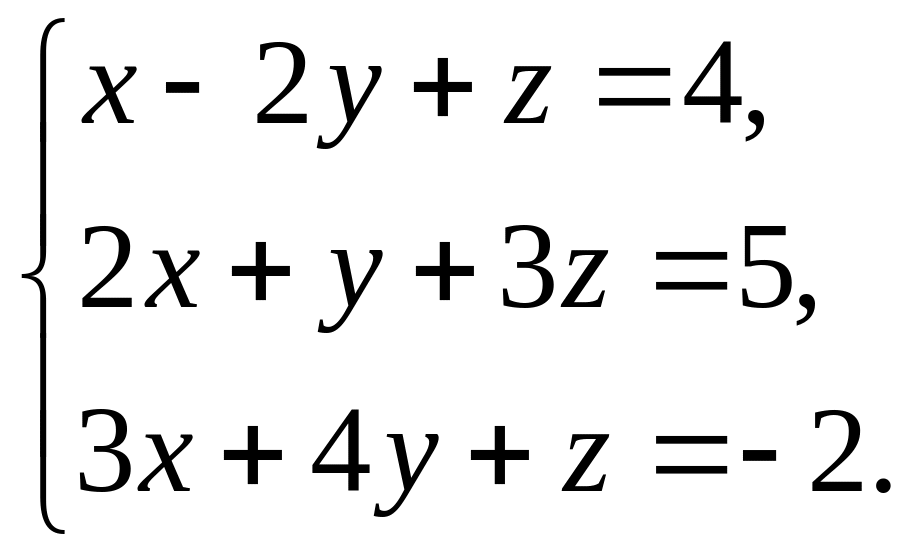 (*)
(*)
Это система трех линейных алгебраических уравнений с тремя неизвестными , которая может быть решена различными способами.
а) Решим систему (*) по формулам Крамера.
Для этого подсчитаем сначала главный
определитель системы
![]() ,
воспользовавшись следующим правилом
вычисления определителей третьего
порядка (разложение определителя по
элементам его первой строки):
,
воспользовавшись следующим правилом
вычисления определителей третьего
порядка (разложение определителя по
элементам его первой строки):
![]() .
.
В нашем случае
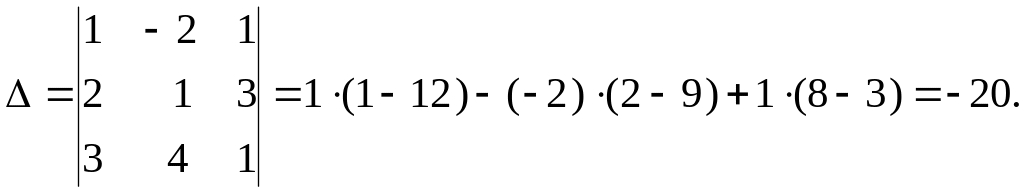
Так как
![]() ,
делаем вывод о том, что система имеет
единственное решение. Для его отыскания
вычислим вспомогательные определители
,
делаем вывод о том, что система имеет
единственное решение. Для его отыскания
вычислим вспомогательные определители
![]() :
:
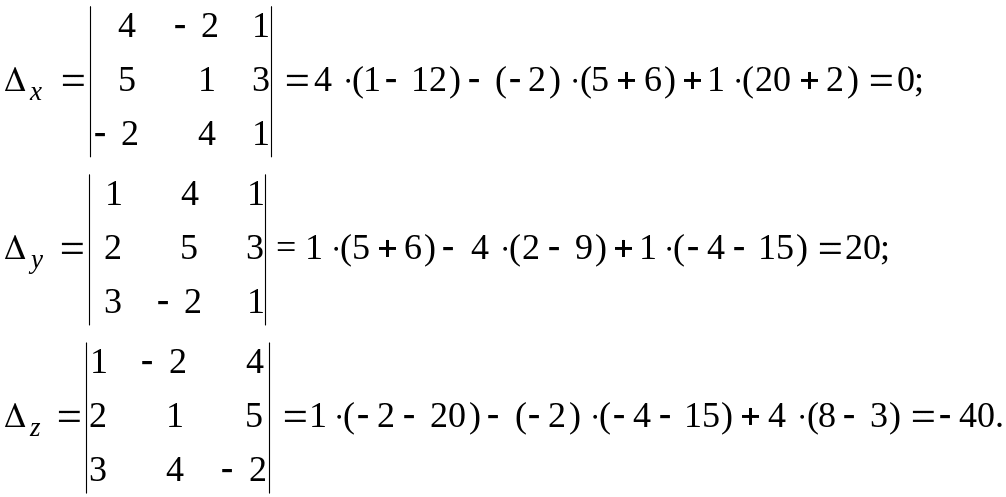
Далее, воспользовавшись формулами Крамера, окончательно получим
![]()
