
3. Поверхности 2-го порядка
На практике наиболее часто используют функции, содержащие целую степень независимых переменных, не превышающих двух. Графики таких функций называют поверхностями 2-го порядка. Для случая функции двух переменных существует пять типов поверхностей 2-го порядка. Их уравнения и графики перечислены ниже.
z



 y
y

x
Рис.
5. Эллипсоид
![]()
z
y
x
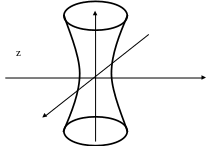
Рис. 6. Однополостный гиперболоид

 z
z
y

z
z
Рис.7
Двуполостный гиперболоид
![]()
z
y
x
Рис.
8. Эллиптический параболоид
![]()
 z
z
y
x
Рис.9.
Гиперболический параболоид
![]()
Задание 2. Дано уравнение линии на координатной плоскости. Найти уравнение поверхности вращения вокруг одной из осей координат и сделать схематический чертеж. Сделать тоже для другой оси.
-
№
Уравнение линии
№
Уравнение линии
1
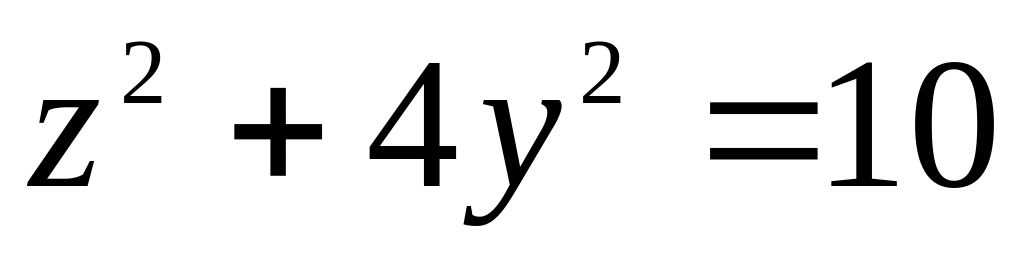
16
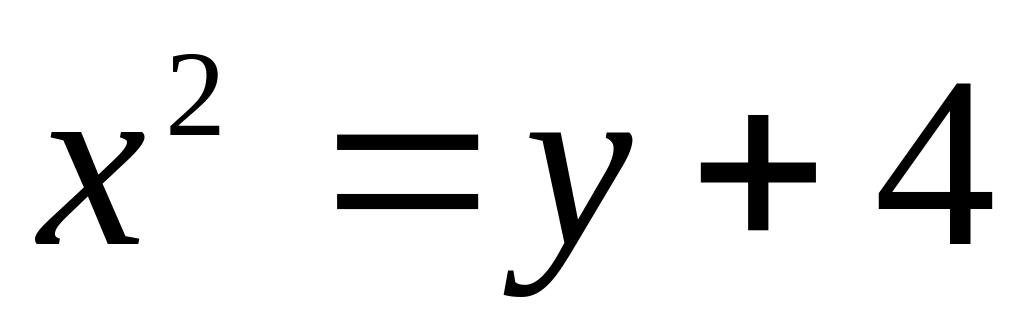
2
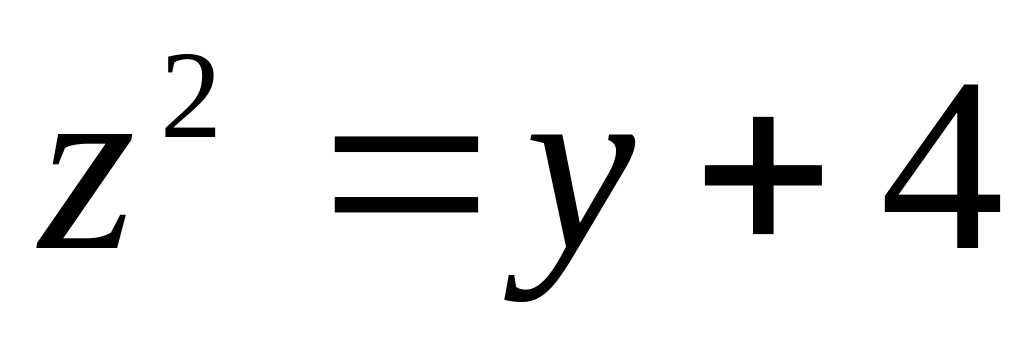
17
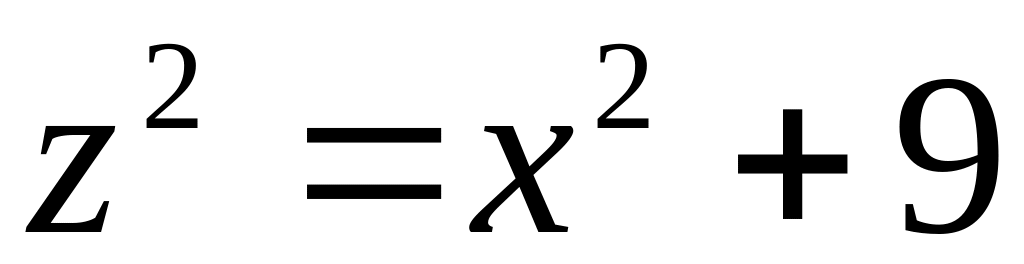
3
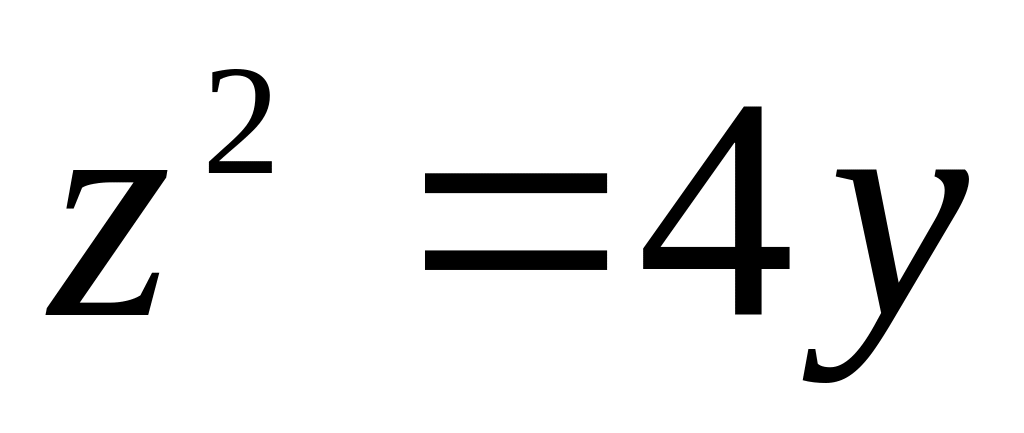
18

4
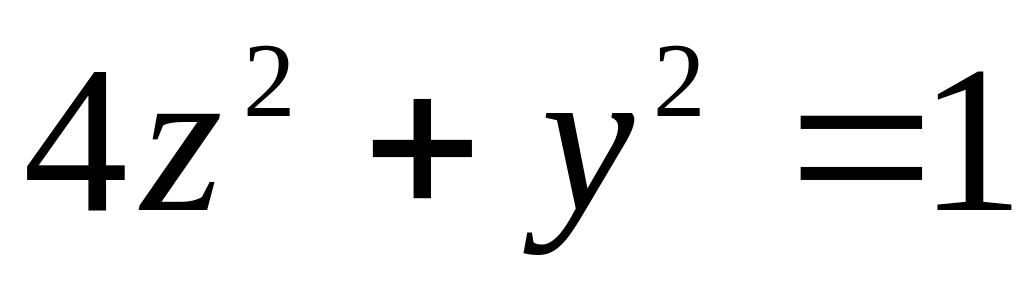
19
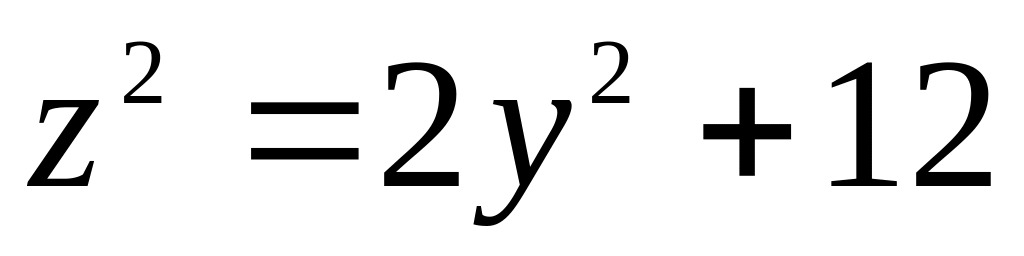
5
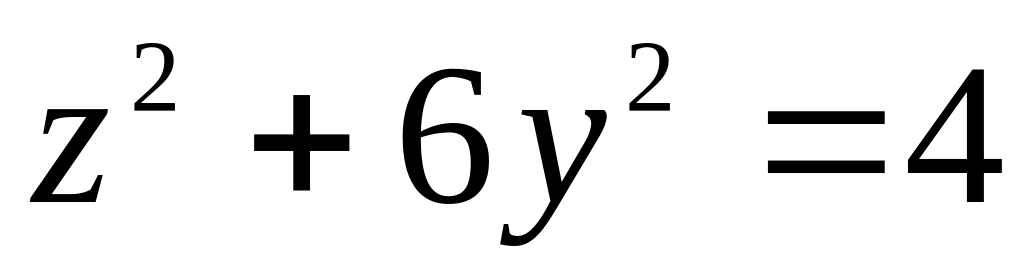
20
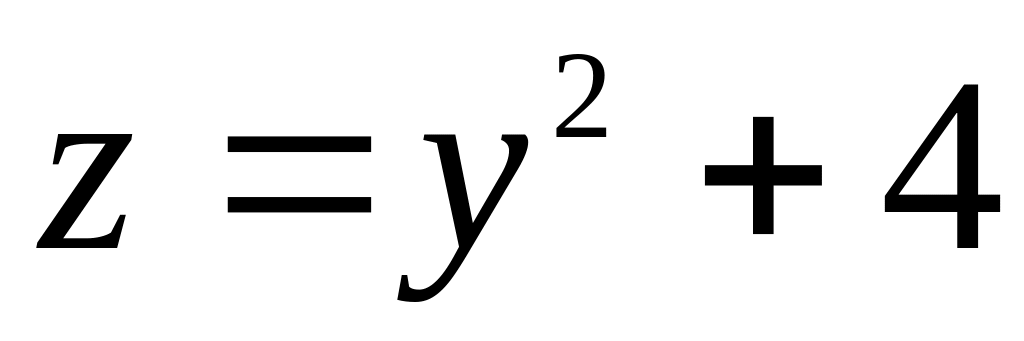
6

21

7

22
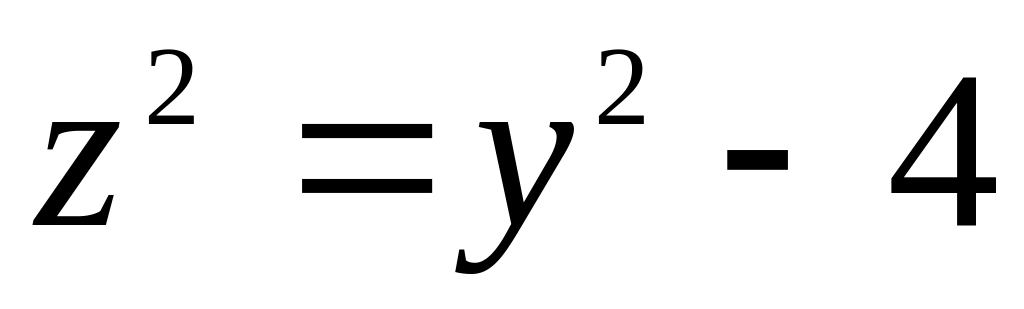
8

23

9
24
10

25

11

26

12
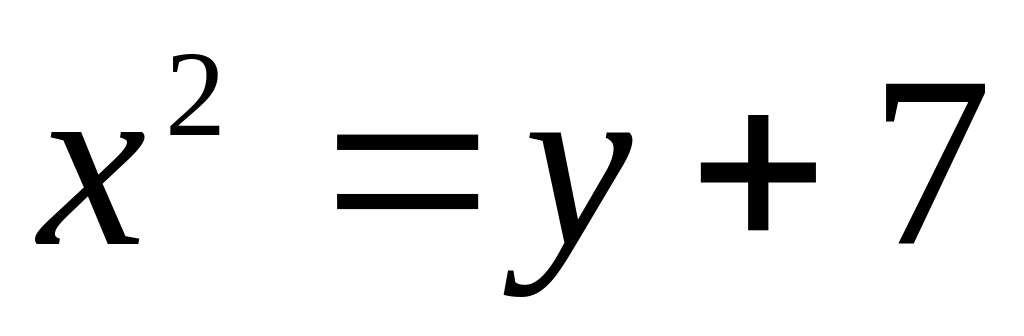
27
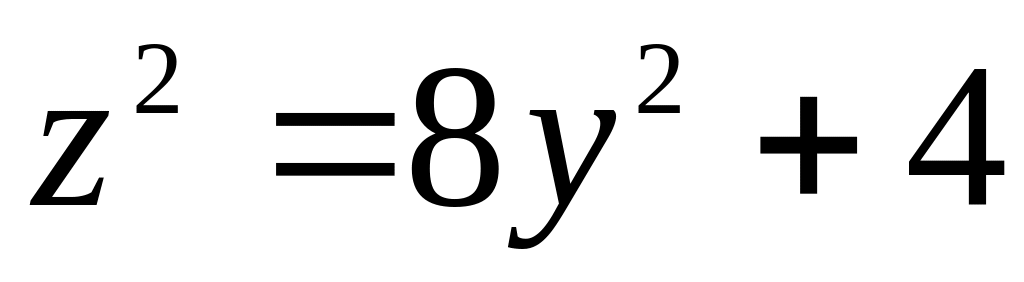
13
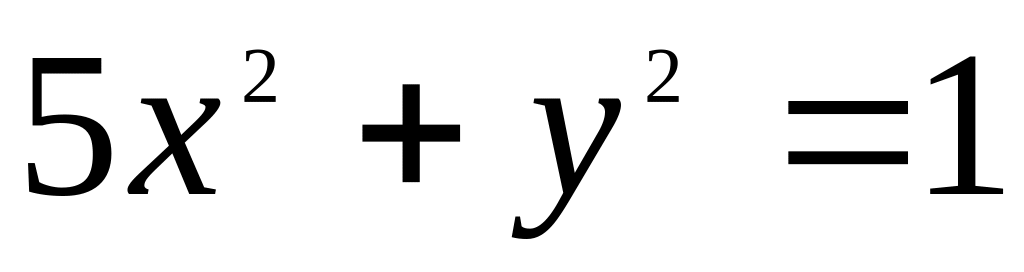
28
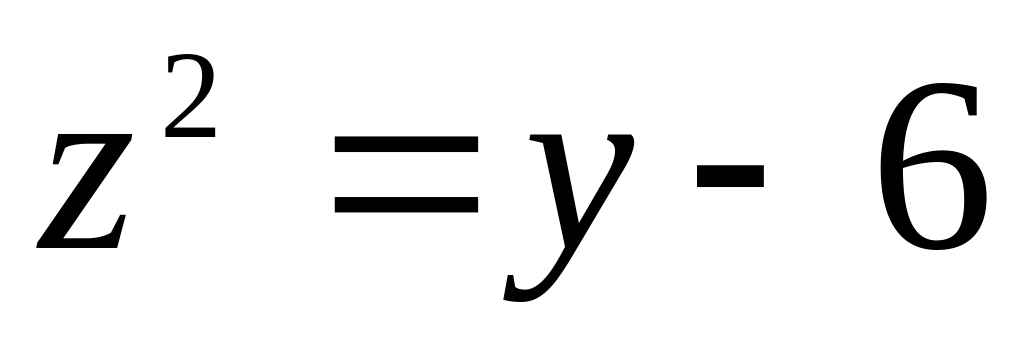
14

29

15
30

Типовой пример. Дано уравнение линии на плоскости. Найти уравнение поверхности вращения вокруг одной из осей координат и сделать схематический чертеж. Сделать тоже для другой оси.
Решение.
Сначала найдем уравнение поверхности
вращения вокруг оси y.
Используем правило: переменная y
остается
без изменения, а вместо переменной z
вставляется выражение
.
Получаем уравнение поверхности вращения
![]() или
или
![]() .
Это уравнение эллипсоида вращения с
полуосями a=
.
Это уравнение эллипсоида вращения с
полуосями a=![]() ,
b=
,
b=![]() ,
c=
(см.
рис. 5).
,
c=
(см.
рис. 5).
При
вращении линии
вокруг оси z
получаем уравнение поверхности вращения
![]() ,
которое тоже является уравнением
эллипсоида вращения, но с другими с
полуосями a=
,
b=
,
c=
.
,
которое тоже является уравнением
эллипсоида вращения, но с другими с
полуосями a=
,
b=
,
c=
.
Задание 3. Даны уравнения поверхностей в пространстве. Построить схематично каждую поверхность в отдельной системе координат; используя эти чертежи, построить тело, ограниченное данными поверхностями.
№ |
Уравнения поверхностей |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
;
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
z=6-y; y=x2; y=4; z=0; (y≤4) |
16 |
z=2y;
|
17 |
z=x2+y2/3; x+y=3; x=0; y=0; z=0 |
18 |
z=2x; y=x2/2; x=2; y=0; z=0 |
19 |
|
20 |
z=y2+2; x=3; y=2; x=0; y=0; z=0 |
21 |
z=9-y2; y=x; y=3; x=0; z=0 |
22 |
|
23 |
z=x2/4+y+1; x+y=4; x=2; x=0; y=0; z=0 |
24 |
|
25 |
z=x+y+2; y=2x; x=3; x=0; y=0; z=0 |
26 |
z=x2+y2; y=x; y=2x; x=2; z=0 |
27 |
z=6-x-y; 2x+y=4; x=0; y=0; z=0 |
28 |
z=12-3x2; 2x+y=4; x=0; y=0; z=0 |
29 |
z=x2+1; 4x+3y-12=0; x=0; y=0; z=0 |
30 |
z=3x+2y;
|
Типовой
пример. Даны
уравнения поверхностей в пространстве
![]() ,
,
,
,
,
,
,
,
![]() .
Построить тело, ограниченное данными
поверхностями.
.
Построить тело, ограниченное данными
поверхностями.
Решение.
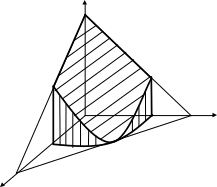
Заданное тело ограничено бесконечным
круговым цилиндром
с радиусом
![]() ,
координатными плоскостями и плоскостью
(см.
рис. 10)
,
координатными плоскостями и плоскостью
(см.
рис. 10)
 z
z
y
x
Рис. 10
