
1. Понятие функции нескольких переменных
При решении многих задач естествознания, экономики и т. д. приходится иметь дело с зависимостями одной переменной от двух, трех и более переменных. Функциональная зависимость в сельском хозяйстве, например, встречается повсюду: начиная с нормы выработки, зависящей от производительности агрегата, и заканчивая различными балансами по использованию земли, техники, трудовых ресурсов и кормов, где все показатели находятся во взаимной связи. Без знания закономерностей количественных взаимосвязей нельзя осуществлять научно обоснованное планирование, сознательно и целеустремленно направлять изучаемые процессы для получения желаемых результатов. В сельском хозяйстве имеется очень много задач из области планирования и расчетов, для решения которых необходимо вскрытие и исследование многофакторных зависимостей и нахождения на этой основе наилучших, то есть оптимальных, вариантов. Приведем примеры функций нескольких переменных.
Пример 1. Объем прямоугольного параллелепипеда V=xyz есть функция трех переменных.
Пример 2. Функция Кобба-Дугласа – производственная функция, показывающая объем выпуска продукции Y при затратах капитала К и трудовых ресурсов L. Для случая двух переменных она имеет вид
![]() ,
,
где А>0 – параметр производительности конкретно взятой технологии, 0<α<1 – доля капитала в доходе.
Определение. Если каждой паре чисел (x,y) из некоторой области D соответствует одно число z, то z есть функция двух независимых переменных x и y, определенная в области D, и обозначается символически z=f(x, y).
Графиком функции двух переменных z=f(x, y) является некоторая поверхность в пространстве Oxyz.
Задание 1. Найти область определения функции z=f(x,y).
№ |
|
№ |
|
№ |
|
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Типовой
пример. Найти
область определения функции
![]() и изобразить схематично на плоскости
Oxy.
и изобразить схематично на плоскости
Oxy.
Решение. Подкоренное выражение должно быть неотрицательным, т.е. 2x+y≥0. Отсюда y≥-2x. Множество точек, координаты которых удовлетворяют этому неравенству, определяют полуплоскость (см. рис. 1).
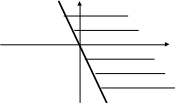 y
y
x
Рис. 1
