1. ДВОЙНОЙ ИНТЕГРАЛ.

ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА

Двойным интегралом от непрерывной функции f(x,y), распространенным на ограниченную область D плоскости x0y, называется предел двумерной интегральной суммы

при max и max , где точки ( , ) принадлежат области D.

Пусть область D определяется неравенствами

,

причем каждая из непрерывных кривых пересекается с прямой, параллельной оси y, только в одной точке.

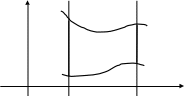
y

y=y₂(x)

D

y=y₁(x)

о x=a x=b x

Рис. 1

В этом случае справедлива формула для вычисления двойного интеграла

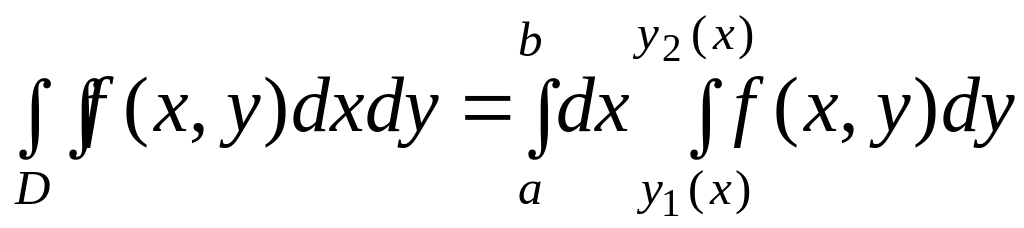, (1)

где при вычислении внутреннего интеграла величину x полагают постоянной.

Если же область D определяется неравенствами

,

причем каждая из непрерывных кривых пересекается с прямой, параллельной оси x, только в одной точке, то двойной интеграл можно вычислить по другой формуле.

В этом случае область D имеет другой стандартный вид

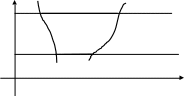
y y=l

D

y=h

x=x₁(y) x=x₂(y)

о x

Рис. 2

Справедлива другая формула для вычисления двойного интеграла

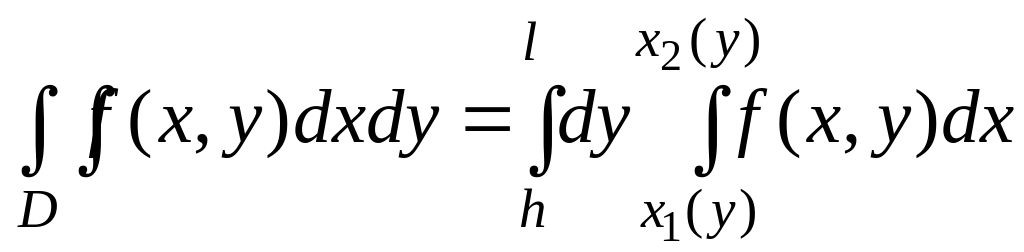, (2)

где при вычислении внутреннего интеграла 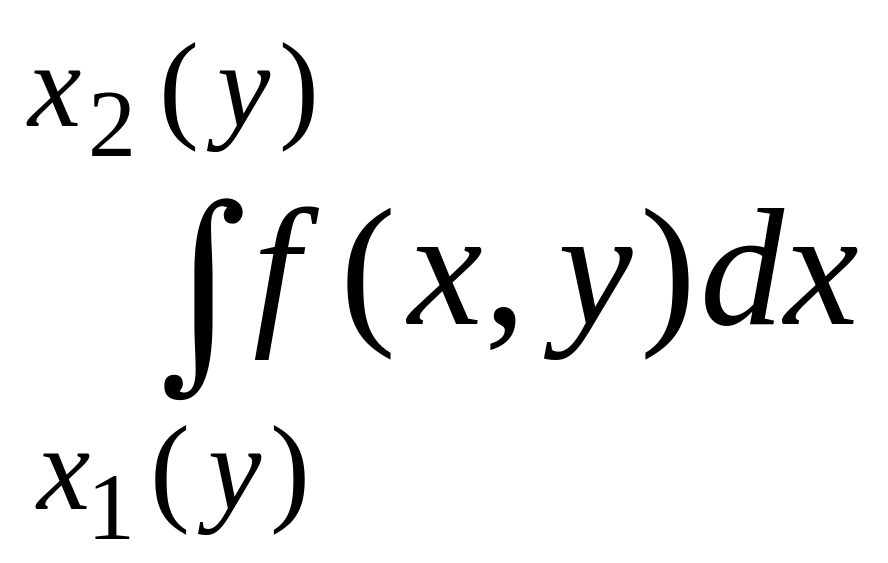величину y полагают постоянной.

Типовые примеры.

1. Вычислить двойной интеграл

.

Решение. Сначала вычисляем внутренний интеграл, где y является переменной величиной, а x постоянной

= - + = =

= .

Далее вычисляем внешний интеграл, т. е. интегрируем полученный результат по переменной x

= = .

Ответ: .

2. Вычислить двойной интеграл

,

если область D ограничена осями координат и прямой y=1-x.

Решение. Строим область интегрирования D.

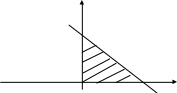y

A(0,1)

x

O B(1,0)

Рис. 3

По формуле (1) имеем

Пределы внешнего интеграла, как правило, всегда постоянны. Это значения абсциссы x крайней левой и крайней правой точек области D

0 ≤ x ≤ 1.

Пределы внутреннего интеграла по y найдем из уравнений линий, ограничивающих область D снизу и сверху

OB: y=0; AB: y=1-x.

Сначала вычислим внутренний интеграл по переменной y , считая x постоянной.

=

= =

= .

Теперь вычислим внешний интеграл по переменной x

= =

= .

Задание 1. Вычислить двойной интеграл , если область D ограничена линиями, указанными в таблице.

№	Интеграл	Область D	Ответы
1		x=0, y=0, x+y=3	9
2		x=1, x=2, y=x, y=2x	9,3
3		y= , y= .
4		x=0, y=0, x+y=1
5		x=1, y=0, y=x
6		y=x, y= , x=2
7		y=x, y= , x=1, x=2	0,9
8		y=x, y= .	0,1
9		y=x, y= , x=1, x=2	-4
10		y=x, y= , x>0
11		xy=1, y= , x=2
12		y=2- , y=2x-1	4
13		x=0, y=0, x+y=1
14		x=1, y=0, y=x	2
15		x=0, y=0, y=x-3
16		x=0, y=0, x=1, y=2	-
17		y=x, y=2x, x=2, x=4.	9
18		x=0, x=lny, y=1, y=2
19		x=-1, x=1, y=-2, y=2	8
20		y= , y=2
21		x=0, y=0, y=2, x=3	36
22		x=0, y=0, y=x+1	2
23		x=0, y=0, y=x+2	-
24		x=0, y=0, 6x+3y=12
25		=x, =y
26		y=x, y= .	0,1
27		x=0, y=0, y=2, x=3	36
28		x=1, y=0, y=x	2
29		x=0, y=0, 6x+3y=12	14
30		y=x, y= .	0,1

8