m32444_5
.doc
ТЕМА 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
В ЗАДАЧАХ 81-100 найти неопределенные интегралы, используя формулы таблицы интегралов и способом подстановки (методом замены переменной).
-
81.
.91.
82.
92.
83.
93.
84.
94.
85.
95.
86.
96.
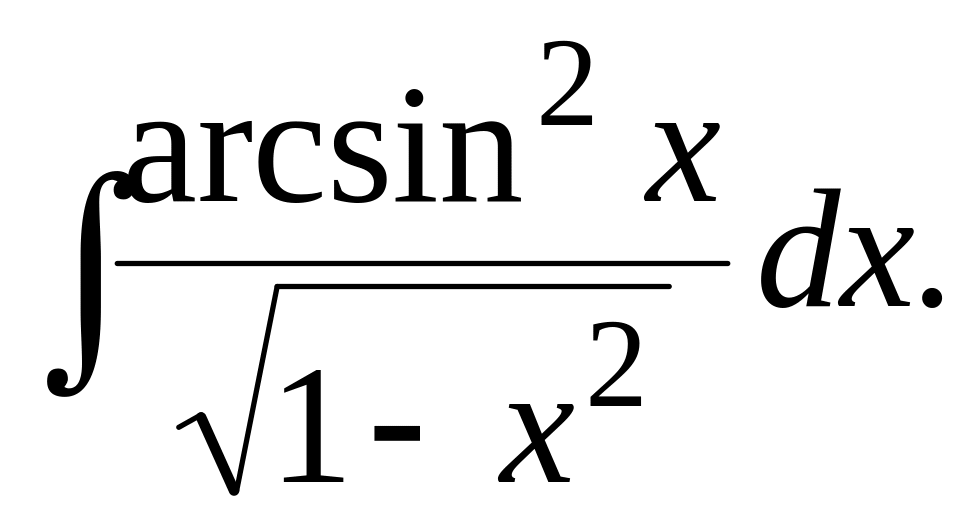
87.
97.
88.
98.
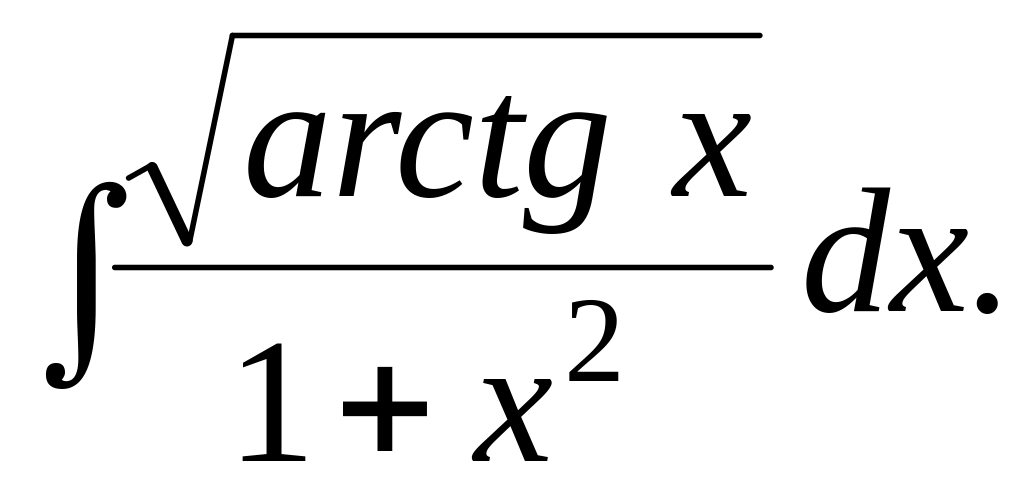
89.
99.
90.
100.
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.
1.Найти неопределенный
интеграл
.
Решение.
Применим подстановку
.
Тогда
и
.
2. Найти неопределенный
интеграл
.
Решение.
Применим подстановку
.
Тогда
,
.
Отсюда
=
=
=
.
В ЗАДАЧАХ 101-110 найти неопределенные интегралы, используя метод выделения полного квадрата.
-
101.
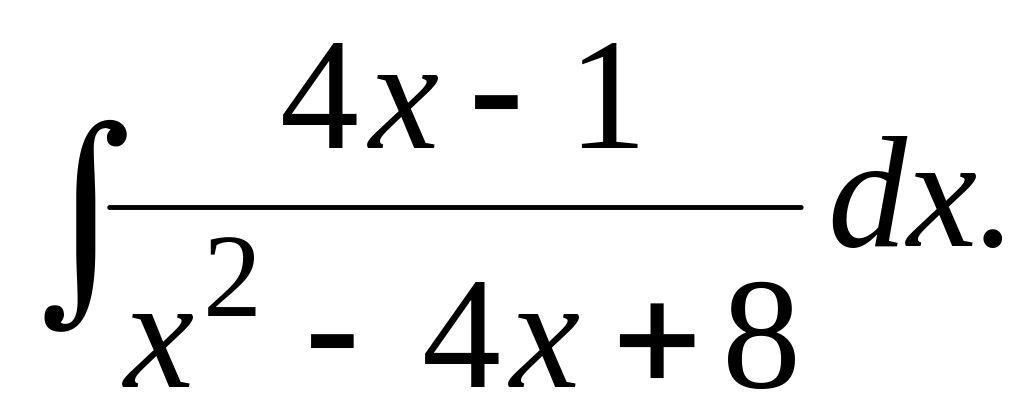
102.
103.
104.
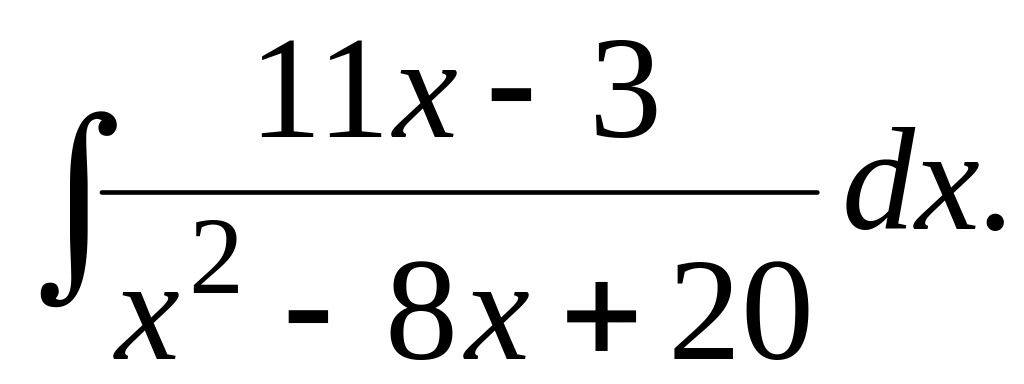
105.
106.
107.
108.
109.
110.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА.
Найти неопределенный
интеграл
.
Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла, следующим образом:
.
Тогда после
подстановки
получим
=
=
=
=
=
+
=
=
= .
ЗАМЕЧАНИЕ.
При вычислении интеграла
использована замена переменной
(подстановка)
.
Тогда
,
откуда
=
=
=
=
.
В ЗАДАЧАХ 111-120 найти неопределенные интегралы, применяя метод интегрирования по частям.
-
111.
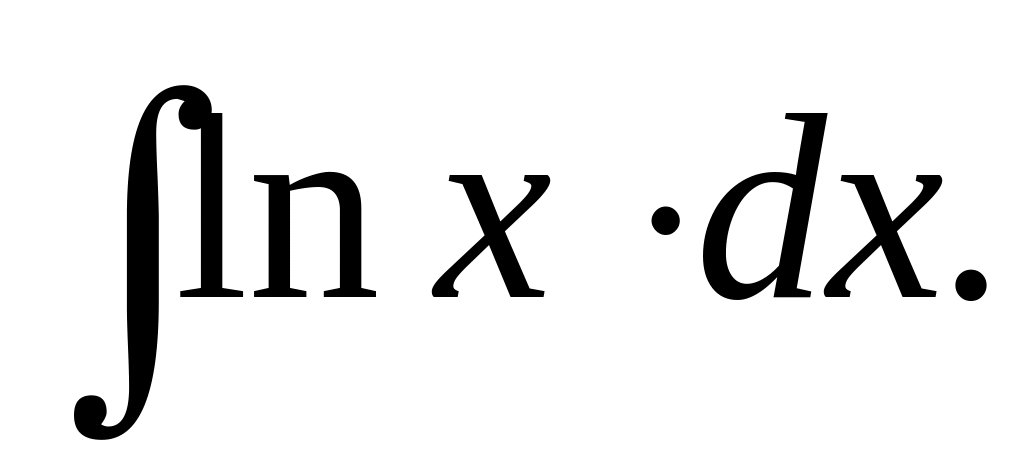
112.
113.
114.
115.
116.
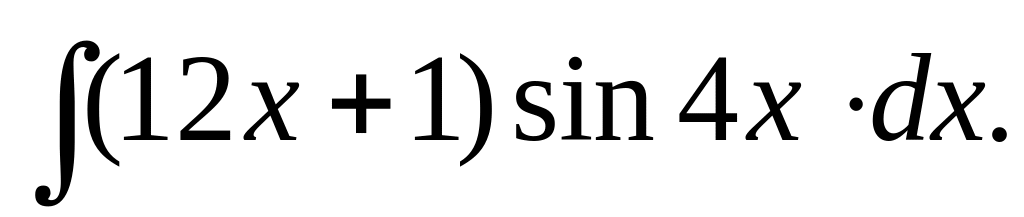
117.
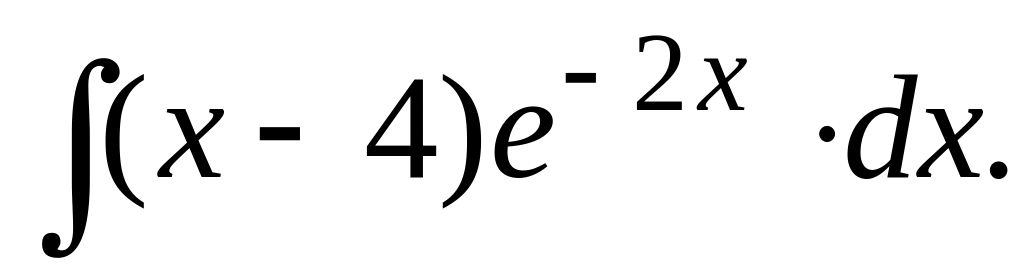
118.
119.
120.
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.
1.
Найти
неопределенный интеграл
.
Решение. Применим формулу интегрирования по частям
.
Положим
,
.
Тогда
,
=
.
Следовательно,
=
=
=
+
.
2.
Найти
неопределенный интеграл
.
Решение.
Положим здесь
,
.
Тогда
,
и
=
.
Применяя в последнем
интеграле подстановку
,
получаем
,
следовательно,
=
=
=
.
Отсюда окончательно имеем:
=
.