
m32352_11
.DOC
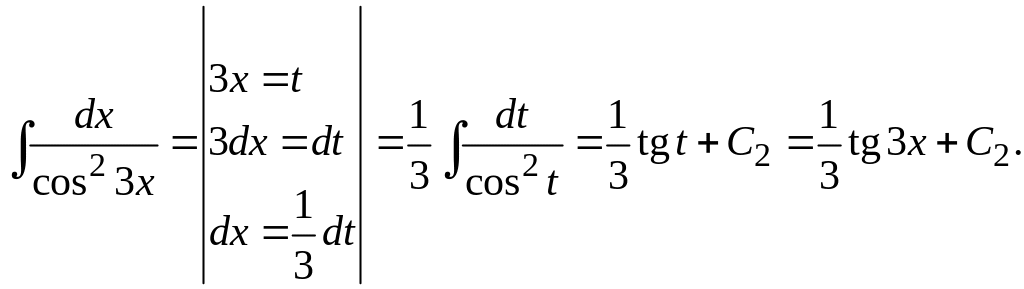
Таким образом, общее решение дифференциального уравнения имеет вид
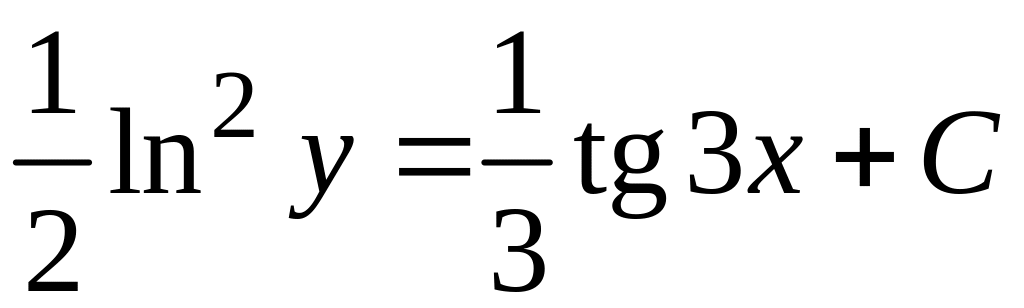
ПРИМЕР 2. Найти частное решение дифференциального уравнения первого порядка, удовлетворяющее заданному начальному условию (решить задачу Коши):
![]()
Решение.
Данное
уравнение является линейным. Разделим
обе его части на
![]() ,
а искомую функцию
,
а искомую функцию
![]() представим
в виде произведения двух других:
представим
в виде произведения двух других:
![]() .
Тогда
.
Тогда
![]() и
исходное уравнение примет вид
и
исходное уравнение примет вид

или
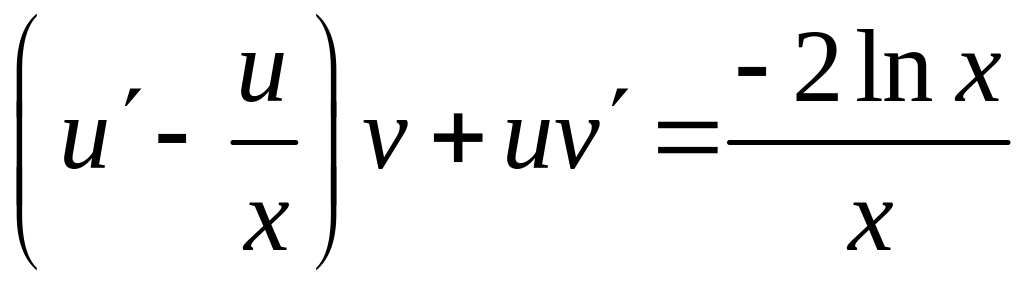 .
(**)
.
(**)
Выберем
функцию
![]() так,
чтобы полученная при группировке скобка
в (**) обратилась в нуль:
так,
чтобы полученная при группировке скобка
в (**) обратилась в нуль:
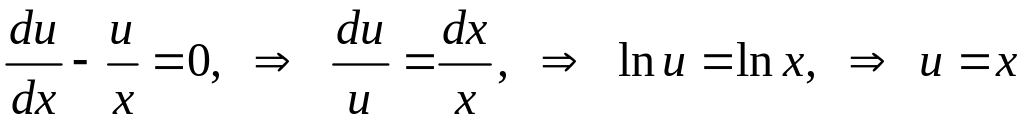
(здесь выбрано частное решение с C = 0 и без знаков модулей).
Подставим в (**). Тогда имеем
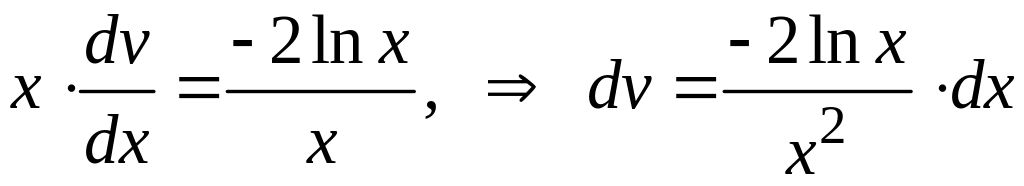 .
.
В
качестве функции
![]() возьмем
общее решение этого дифференциального
уравнения первого порядка с разделяющимися
переменными:
возьмем
общее решение этого дифференциального
уравнения первого порядка с разделяющимися
переменными:
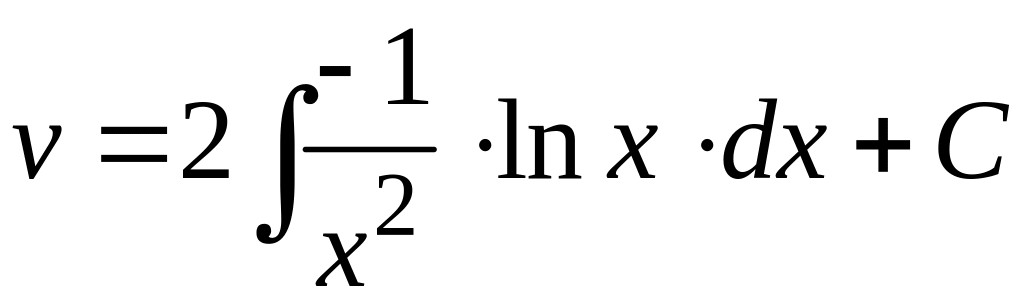 .
.
Вычислим интеграл с помощью формулы интегрирования по частям:
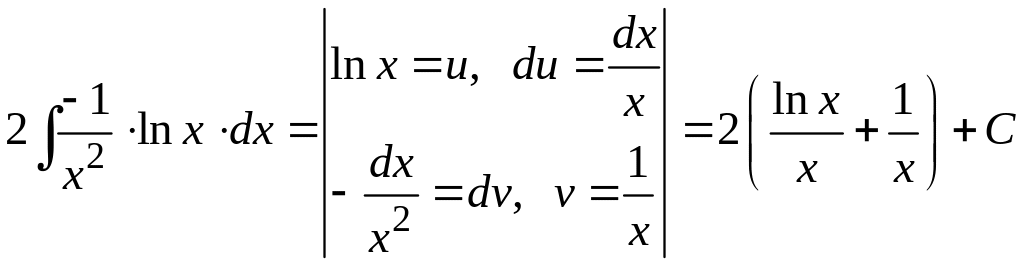 .
.
Таким
образом,
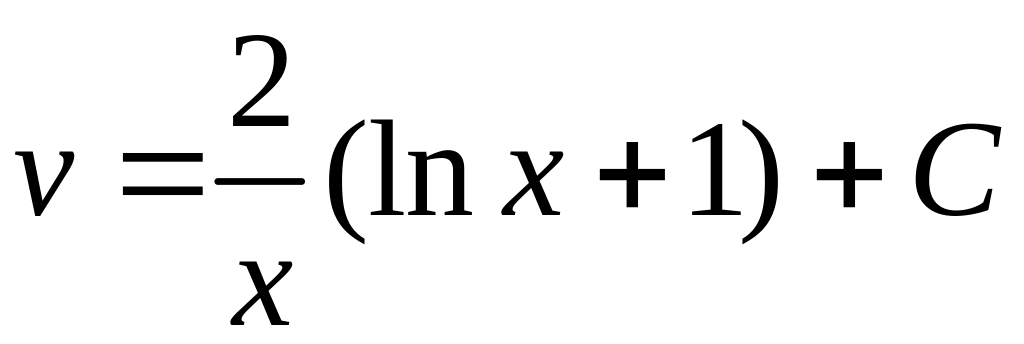 ,
а общее решение исходного уравнения
имеет вид
,
а общее решение исходного уравнения
имеет вид
![]() .
.
Теперь
для нахождения значения произвольной
постоянной C
воспользуемся начальным условием
![]() .
Тогда имеем
.
Тогда имеем
0,2=2(ln1 + 1)+C,
откуда
0,2=2(0+1)+C,
![]() С= –
1,8.
С= –
1,8.
Итак, искомое частное решение имеет вид
![]() .
.
ПРИМЕР 3. Найти частные решения следующих линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами при заданных начальных условиях:
1) |
|
|
|
2) |
|
|
|
3) |
|
|
|
Решение.
1)
Характеристическое уравнение
![]() имеет два различных вещественных корня
имеет два различных вещественных корня
![]() ,
,
![]() ,
поэтому общее решение этого дифференциального
уравнения записывается в виде
,
поэтому общее решение этого дифференциального
уравнения записывается в виде
![]() ,
,
где
![]() ,
,
![]()
произвольные постоянные.
произвольные постоянные.
Отсюда
![]() .
.
Используя начальные условия, получаем
![]() ,
т.е.
,
т.е.
![]() ,
,
и
![]() ,
т.е.
,
т.е.
![]() .
.
Решая систему уравнений
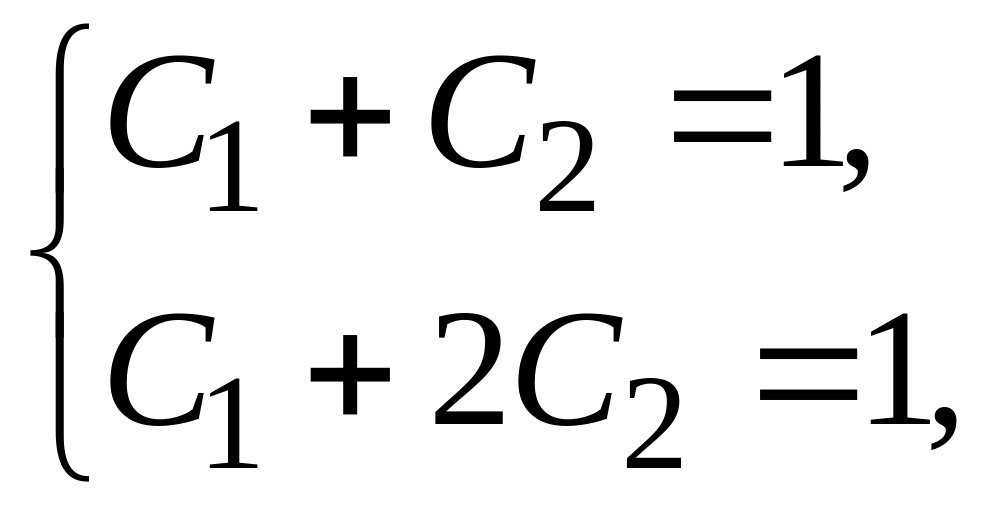
получаем
![]() ,
,
![]() .
Частное решение исходного уравнения,
удовлетворяющее заданным начальным
условиям, найдено и имеет вид
.
Частное решение исходного уравнения,
удовлетворяющее заданным начальным
условиям, найдено и имеет вид
![]() .
.
2)
Характеристическое уравнение
![]() имеет два равных корня
имеет два равных корня
![]() ,
поэтому общее решение соответствующего
дифференциального уравнения записывается
в виде
,
поэтому общее решение соответствующего
дифференциального уравнения записывается
в виде
![]() ,
,
откуда
![]() .
.
Учитывая начальные условия, получаем систему уравнений для определения , :
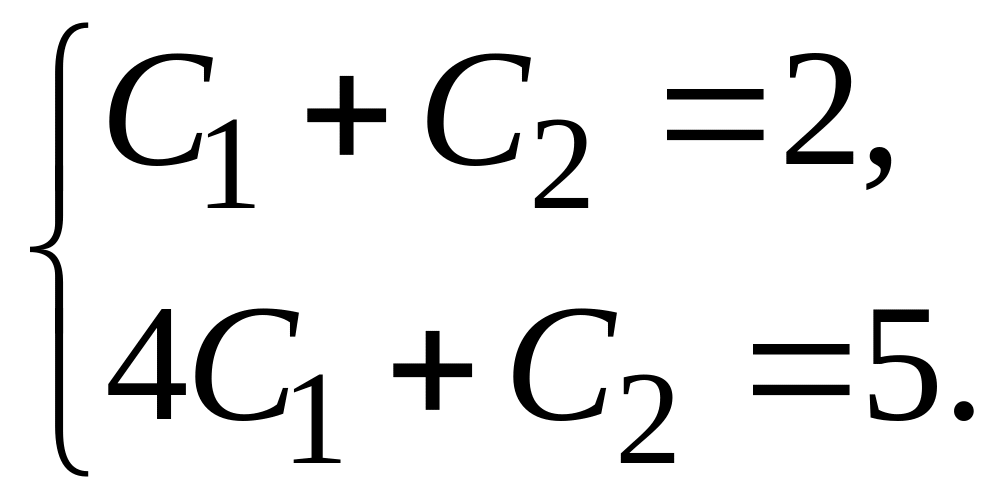
Отсюда
;
![]() ,
поэтому искомое частное решение имеет
вид
,
поэтому искомое частное решение имеет
вид
![]() .
.
3)
Характеристическое уравнение
![]() имеет комплексно-сопряженные корни
имеет комплексно-сопряженные корни
![]() ,
поэтому общее решение соответствующего
дифференциального уравнения записывается
в виде
,
поэтому общее решение соответствующего
дифференциального уравнения записывается
в виде
![]() .
.
Отсюда
![]() .
.
Таким образом, для определения значений , , исходя из начальных условий, получаем систему уравнений
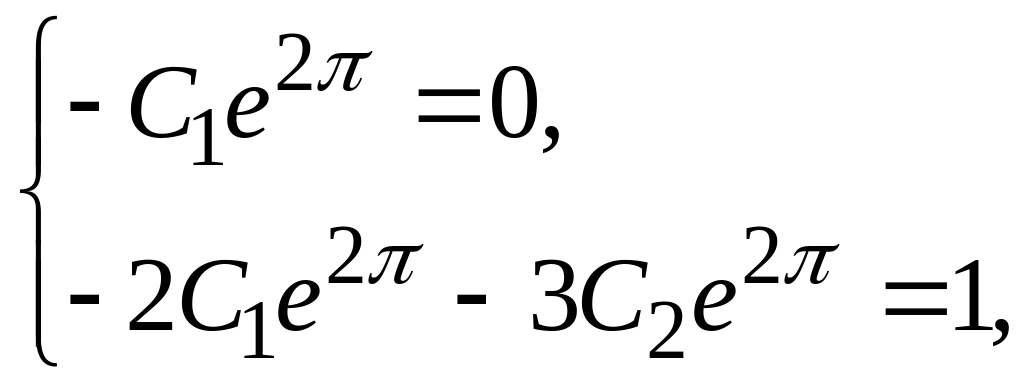
решая
которую, имеем
![]() ,
,
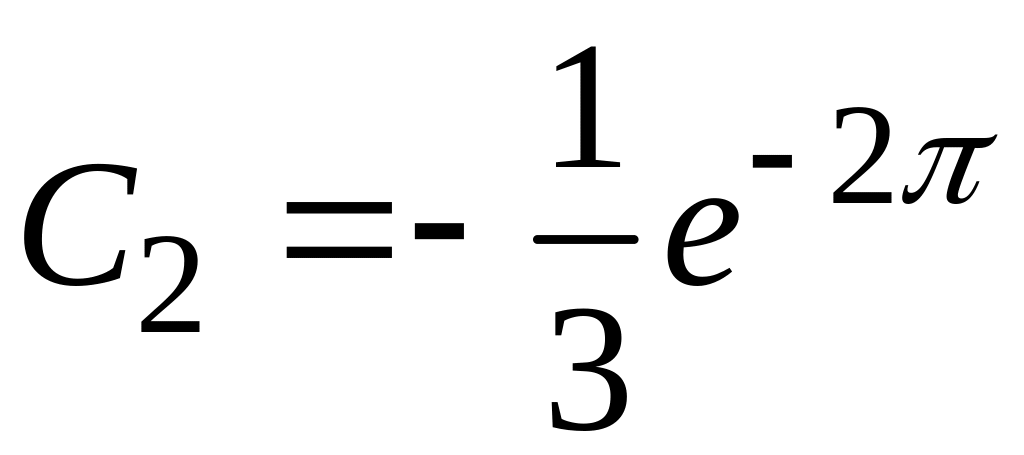 .
.
Таким образом, искомое частное решение имеет вид
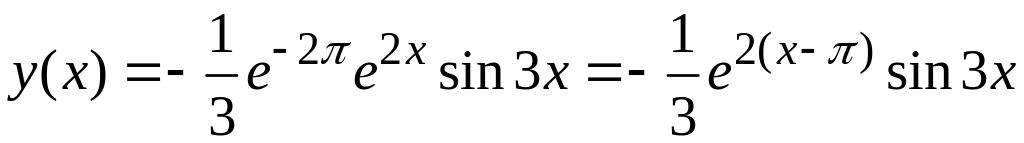 .
.
ПРИМЕР 4. Найти общие решения следующих линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
1)![]() ;
2)
;
2)
![]() .
.
Решение.
1)
Найдем общее решение
![]() линейного однородного уравнения с теми
же коэффициентами, что и в левой части
заданного:
линейного однородного уравнения с теми
же коэффициентами, что и в левой части
заданного:
![]()
Так
как корни его характеристического
уравнения
![]() действительны и различны (
действительны и различны (![]() ;
;
![]() ),
то общее решение однородного уравнения
записывается в виде
),
то общее решение однородного уравнения
записывается в виде
![]() ,
,
где , произвольные постоянные.
Правая
часть заданного неоднородного уравнения
относится к виду
![]() ,
где
,
где
![]() многочлен степени n
от переменной x.
В нашем случае
многочлен степени n
от переменной x.
В нашем случае
![]()
![]() ,
поэтому, учитывая совпадение одного из
корней характеристического уравнения
с параметром а,
подбираем частное решение исходного
неоднородного уравнения по формуле
,
поэтому, учитывая совпадение одного из
корней характеристического уравнения
с параметром а,
подбираем частное решение исходного
неоднородного уравнения по формуле
![]() ,
,
где А, В неопределенные коэффициенты. Для отыскания их значений находим
![]() ,
,
![]()
![]() .
.
Подставляя
![]() ,
,
![]() ,
,
![]() в исходное уравнение и сокращая все
слагаемые на множитель
в исходное уравнение и сокращая все
слагаемые на множитель
![]() ,
получаем
,
получаем
![]()
![]()
или, после упрощения,
![]() .
.
Отсюда следуют равенства
![]() ,
,
![]() ,
т.е.
,
т.е.
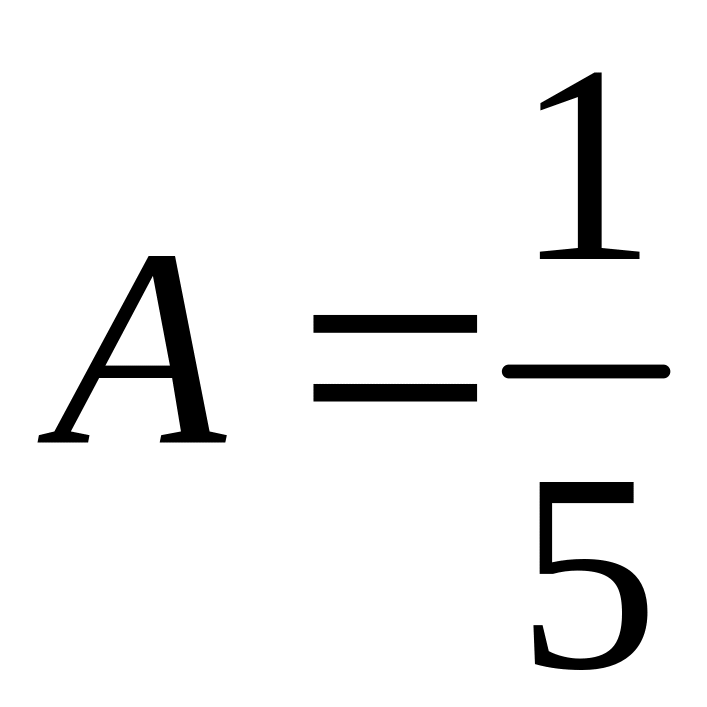 ,
,
 .
.
Таким образом, общее решение заданного неоднородного дифференциального уравнения имеет вид
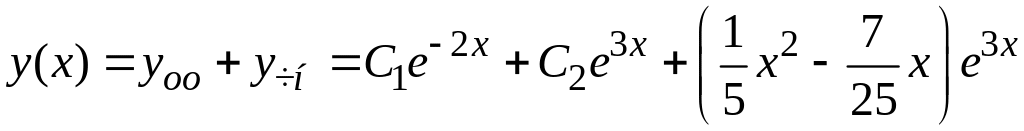 .
.
2) Решаем характеристическое уравнение:
![]() .
.
Отсюда записываем общее решение однородного уравнения:
![]() .
.
Так
как правая часть заданного неоднородного
уравнения относится к типу
![]() и имеется совпадение одного
и имеется совпадение одного
