
m35674_19
.DOC
Sfact
![]()
![]()
![]()
Sfact = 17.025
Sostat
![]()
![]()
![]()
Sostat = 46.044
3. Вычисляем исправленные выборочные факторную и остаточную дисперсии:
S2F
![]() S2OST
S2OST
![]()
S2F = 8.513 S2OST = 3.837
4. Находим наблюдаемое значение критерия Фишера:
F1
![]() F1 = 2.219
F1 = 2.219
5. Вычисляем вероятность того, что значение критерия Фишера с числом степеней свободы числителя k1 и знаменателя Nk превысит F1. Если полученная вероятность окажется меньше заданного уровня значимости =0,05, то принимается гипотеза о значимости влияния фактора А. В противном случае считается, что значимость фактора осталась недоказанной. В нашем случае имеем
Fkr 1 pF(F1,k1,Nk) Fkr = 0.151
Таким образом, в рассматриваемом примере нам не удалось подтвердить значимость влияния фактора А на 5% и даже на 10% и 15% уровнях значимости.
Простая парная регрессия
Имеются следующие данные об урожайности y сельскохозяйственной культуры в зависимости от дозы удобрений x:
x(0 20 60 90 120 150)
y(27.4 34.9 38.5 46.6 55.5 67.1)
Введем постоянные
k n6
где k – число объясняющих факторов, а n – число наблюдений в выборке.
1. Рассчитаем коэффициент корреляции между предсказывающим фактором х и результирующим фактором y, а также параметры a, b уравнения регрессии y=a + bx, получаемые по методу наименьших квадратов. Имеем:
corr![]() = 0.982
= 0.982
a intercept a = 26.914
b slope b = 0.247
Итак, коэффициент корреляции 0,982 весьма высокий, что свидетельствует о наличии тесной связи между фактором x и откликом y.
Уравнение простой парной регрессии имеет вид
y= 26.914 + 0.247*x.
2. Проведем дисперсионный анализ качества модели и проверим гипотезу о значимости уравнения регрессии. Для этого получим расчетные значения модели y1 и вектор остатков e:
y1 a + b x y1 = (26.914 31.846 41.712 49.111 56.51 63.909)
e y y1 e = (0.486 3.054 3.212 2.511 1.01 3.191)
Вычислим сумму квадратов модели S2mod и остаточную сумму квадратов S2ost:
S2mod
(y1
mean(y)) ![]() S2mod = (1017.856)
S2mod = (1017.856)
S2ost
e
![]() S2ost = (37.384)
S2ost = (37.384)
Для проверки значимости модели составим дисперсии модели и ее остатков, разделив суммы квадратов на соответствующие степени свободы этих сумм:
Smod
![]() Smod = (1017.856)
Smod = (1017.856)
Sost
![]() Sost = (9.346)
Sost = (9.346)
Наблюдаемое значение критерия Фишера равно отношению полученных дисперсий:
F![]() F = (108.909)
F = (108.909)
Выберем некоторый стандартный уровень значимости, например 0.05.
Если мы считаем гипотезу о незначимости уравнения регрессии нулевой, а альтернативной является гипотеза о значимости этого уравнения, то вероятность превышения наблюдаемого значения критерия Фишера не должна быть меньше 0.05. В противном случае нулевую гипотезу отвергают и принимают гипотезу о значимости уравнения регрессии. Вычисляем:
1
pF(F,
k, nk1)
=
![]()
Полученная вероятность меньше 0.05, следовательно, мы признаем уравнение регрессии значимым.
3. Проведем процедуру проверки значимости коэффициентов регрессии а и b. Для этого вычислим средние квадратические отклонения коэффициентов:
sb![]() sb = (0.072) sa
sb
sb = (0.072) sa
sb![]() sa = (6.529)
sa = (6.529)
Затем вычисляем наблюдаемые значения критерия Стьюдента для коэффициентов а и b и вероятности их превышения при использовании двустороннего критерия:
ta![]() ta = (4.122) tb
ta = (4.122) tb
![]() tb = (3.414)
tb = (3.414)
![]()
![]()
Как видим, оба коэффициента уравнения значимы на 95% уровне значимости. Это можно было бы доказать и другим способом, вычислив критическое значение двустороннего критерия Стьюдента при 95% уровне значимости:
0.95
1
qt![]() = 2.306
= 2.306
Так как наблюдаемые значения ta=4.122 и tb=3.414 больше критического значения 2.306, следует признать, что коэффициенты уравнения значимы.
4. Построим доверительные интервалы для прогноза по уравнению простой парной регрессии.
Сначала вычисляем среднеквадратическую ошибку расчетных значений результирующего признака y1 в некоторой точке х1:
Sy1(x1)Sost![]()
Выберем некоторый уровень надежности , например, равный 0.95. Тогда доверительный интервал для расчета прогноза Y1(x1) вычисляется в соответствии с формулами
Y1(x1)a + b x1
Y1left(x1)
Y1(x1)
qt![]() Sy1(x1)
Sy1(x1)
Y1right(x1) Y1(x1) + qt Sy1(x1)
Получаем:
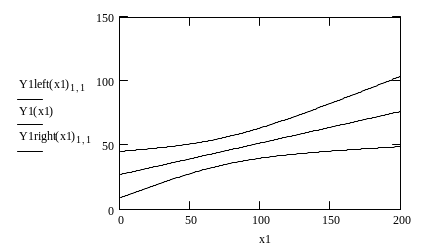
Y1left(50) = (27.664) |
|
Y1right(50) = (50.827) |
Y1left(100) = (39.71) |
|
Y1right(100) = (63.444) |
Y1left(150) = (45.234) |
|
Y1right(150) = (82.583) |
Изобразим прямую Y1=26.914+0.247*x1 и доверительный интервал для этой прямой:
Для индивидуальных значений результирующего признака Y доверительный интервал прогнозируемых значений рассчитывается по формулам
Syind(x1)Sost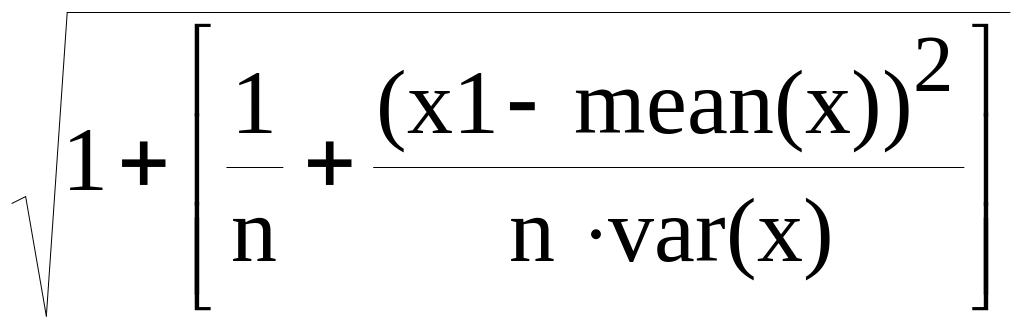
Y1left(x1) Y1(x1) qt Syind(x1)
Y1right(x1) Y1(x1) + qt Syind(x1)
Получаем:
Y1left(50) = (10.83) |
|
Y1right(50) = (67.661) |
Y1left(100) = (23.043) |
|
Y1right(100) = (80.11) |
Y1left(150) = (31.939) |
|
Y1right(150) = (95.878) |
СПИСОК ЛИТЕРАТУРЫ
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.M.: Высшая школа, 1999. 400 с.
Гмурман В.Е. Теория вероятностей и математическая статистика.М.: Высшая школа, 1999. 479 с.
Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов.М.: ЮНИТИ-ДАНА, 2001. 543 с.
Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика.M.: Высшая школа, 1991. 400 с.
Алейников С.М., Дементьева А.М. Элементы теории вероятностей и математической статистики: Курс лекций /Воронеж. гос. архитект.-строит. ун-т. – Воронеж, 2002.84 с.
Решение задач математической статистики с использованием персонального компьютера: Учебное пособие для студентов инженерно-технических специальностей сельскохозяйственных вузов /Дементьев С.Н., Стрыгина С.О., Яновский Л.П., Ясаков А.И. Воронеж: ВГАУ, 1999. 136 с.
Практикум по теории вероятностей: Методические указания для студентов факультета ветеринарной медицины ВГАУ /Стрыгина С.О., Дементьев С.Н., Слиденко А.М., Чернышова Г.И. Воронеж: ВГАУ, 1998. 66 с.
Теория вероятностей: Учебное пособие для студентов факультета ветеринарной медицины ВГАУ /Стрыгина С.О., Дементьев С.Н., Слиденко А.М., Чернышова Г.И. Воронеж: ВГАУ, 2001. 97 с.
Кудрявцев Е.М. Mathcad 2000 Pro.М.: ДМК Пресс, 2001. 576 с.

