m33255_3

3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР

С ПОМОЩЬЮ ДВОЙНОГО ИНТЕГРАЛА

Площадь S плоской фигуры D вычисляется по формуле

.

Если область D стандартного вида, то двойной интеграл сводится к повторным интегралам. В противном случае область D необходимо разбить на несколько областей, которые должны быть областями стандартного вида.

Типовой пример. Вычислить площадь фигуры, ограниченной прямой y=2x+1 и параболой y=x²+1.

Решение.

Найдем координаты точек пересечения прямой и параболы. Для этого решаем совместно систему уравнений этих линий.

Получаем . Отсюда находим координаты точек A(0;1) и B(2;5).

Построим область D в системе координат x0y.

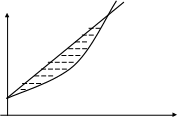
y B(2,5)

y=2x+1

y=x²+1

A(0,1)

x

Рис. 5

Теперь вычислим площадь области D, используя формулу (2) вычисления двойного интеграла

.

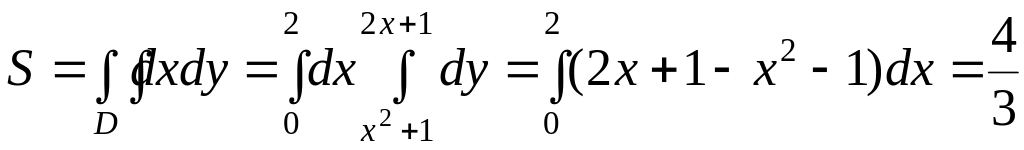Задание 3. Вычислить площади областей, ограниченными линиями, с помощью двойных интегралов

№	Линии, ограничивающие область D	Ответы
1	xy=4, y=x, x=4.	6-4ln2
2	y=x2, 4y=x2, y=4
3	y2=4+x, x+3y=0
4	y=x, y=2-x2
5	y=x2, y=x+2
6	y=sinx, y=cosx, x=0
7	, y=4x-4
8	, y=2x-4
9
10
11	, y=2x-4	12
12
13
14	, y=2x	8
15	y=2x-3
16
17	, y=x+1
18	, y=x-1	6
19		8
20		9
21
22	.
23		6
24	, y=3x-3
25	y=8-3x,
26	xy=4, y=x, x=4.	6-4ln2
27	y=x2, 4y=x2, y=4
28	y2=4+x, x+3y=0
29	y=x, y=2-x2
30	y=x2, y=x+2

14