
- •Литература
- •Лекция №1 Колебания и волны
- •Примеры решения задач
- •Колебательные системы в биологии и медицине
- •2. Механические волны
- •Примеры решения задач
- •Ультразвук
- •Эффект Доплера
- •Диагностическое применение эффекта Доплера
- •Примеры решения задач
- •Лекция №2 Течение и свойства жидкостей
- •Примеры решения задач
- •Формула Пуазейля
- •Примеры решения задач
- •Примеры решения задач
- •Лекция №3 Электростатика
- •4. Работа перемещения заряда в электрическом поле. Потенциал.
- •5. Использование электрического поля в медицине.
- •Примеры решения задач
- •Лекция №4 Контактные явления
- •Лекция №5 Электромагнетизм
- •5. Магнитные свойства тканей организма. Физические основы магнитобиологии.
- •Примеры решения задач
- •Лекция №6
- •2. Частица в электрическом поле
- •4. Электромагнитные счетчики скорости крови
- •Примеры решения задач
- •Лекция №7
- •Примеры решения задач
- •Лекция №8 Электрические колебания и электромагнитные волны
- •Примеры решения задач
- •Лекция №9 Оптика
- •4. Эндоскопическая аппаратура и ее применение в клинической практике.
- •Примеры решения задач
- •Лекция №10 Волновые свойства света
- •Примеры решения задач
- •Лекция №11
- •Примеры решения задач
- •Лекция №12 Квантовые свойства света и строение атома
- •Примеры решения задач
- •4. Дискретность энергетических состояний атома. Постулаты Бора.
- •5. Квантовая теория строения атома водорода.
- •Примеры решения задач
- •Лекция №13 Рентгеновское излучение, его использование в медицине
- •3. Использование р.И. В медицинской практике
- •Лекция №14 Лазерное излучение, его использование в медицине.
- •4.Использование лазера в медицине
- •Примеры решения задач
- •Лекция №15 Магнито-резонансные явления, их применение в медицине.
- •Примеры решения задач
- •Лекция №16 Основы ядерной физики. Понятия ядерной медицины.
- •Примеры решения задач
Литература
1. Ремизов А.Н. «Медицинская и биологическая физика»,М.2001 г.
2. Блохина М.Е., Эссаулова И.А. и др. «Руководство к лабораторным работам по медицинской и биологической физике»
3. Кумыков. В.К., Захохов Г.М. «Физические методы в функциональной диагностике» Нальчик, КБГУ,2006
4. Кумыков. В.К., Абазова З.Х «Физические методы в медицинских технологиях» Нальчик, КБГУ, 2004
Лекция №1 Колебания и волны
Гармонический осциллятор. Колебательные системы в биологии и медицине.
Механические волны, их уравнение. Вектор Умова. Ультразвук, его применение в медицине.
Эффект Доплера, его медицинские приложения
1. Колебания гармонического осциллятора являются очень важным примером периодического движения. К числу классических систем, аналогичных гармоническому осциллятору, относятсялюбые системы , которые, будучи слегка выведены из положения равновесия, совершают устойчивые колебания. К ним относятся:
Математический маятник в пределах малых углов отклонения.
Масса на пружине в пределах малых амплитуд колебаний
Колебательный контур , состоящий из конденсатора и катушки
Частота колебаний осциллятора не зависит от амплитуды.
Математический маятниксостоит из материальной (∙) массойm, расположенной на нижнем конце невесомого стержня длинойL, свободно вращающегося вокруг оси, проходящей через верхний конец.
Выведем уравнение колебаний маятника.
Проще всего записать уравнение F=ma,
однако поучительнее будет решить
поставленную задачу через закон
сохранения энергии. Отклонение маятника
определяется углом![]() ,
который стержень образует с вертикалью.
,
который стержень образует с вертикалью.

![]() (1)
(1)
Потенциальная энергия маятника
U(![]() )=Mgh(2)
)=Mgh(2)
![]()
![]() (3)
(3)
Кинетическая энергия маятника равна
![]() (4)
(4)
Полная энергия маятника равна
![]()
![]()
![]() (5)
(5)
Принимая во внимание, что ![]() (6)
(6)
 (7)
(7)
Решая это уравнение относительно
![]() находим
находим
![]() (8)
(8)
При
![]()
![]() .
Тогда из (7) получим с учетом того, что
.
Тогда из (7) получим с учетом того, что![]() :
:
![]() ,
,![]() (9)
(9)
Тогда (8) перепишется в виде:
![]() (10)
(10)
Или
 (11)
(11)
Этот вид удобен для интегрирования.
Если начальные условия таковы, что при
![]()
![]() ,
то
,
то
 (12)
(12)
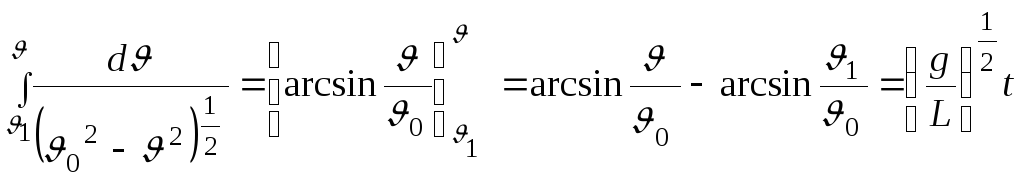 (13)
(13)
Так как
![]() ,
то (13) запишется
,
то (13) запишется
![]() (14)
(14)
Или
![]() (15)
(15)
Где
![]() -
круговая частота
-
круговая частота
![]() -фаза
-фаза
Период колебаний математического
маятника
![]()
пружинного
![]()
колебательного контура
![]()
Примеры решения задач
1. Материальная точка массой 5 г. колеблется
согласно уравнению
![]() .
Найти максимальную силу, действующую
на точку и полную энергию.
.
Найти максимальную силу, действующую
на точку и полную энергию.
Решение
Сила, действующая на материальную точку,
равна
![]() .
Ускорение
.
Ускорение![]() может быть найдено как вторая производная
смещения
может быть найдено как вторая производная
смещения![]() по
времени. Первая производная
по
времени. Первая производная![]() .
Вторая производная
.
Вторая производная![]() .
Максимальное значение косинуса -1,
.
Максимальное значение косинуса -1,![]() и
и![]()
![]()
![]()
Колебательные системы в биологии и медицине
Большинство процессов, анализ которых дает основной объем диагностической информации, имеют колебательный характер. В технике это механические, электромагнитные и др. виды колебаний. В биологии и медицине - ритмы, циклы и т.д. Циклами называют периодические изменения свойств биологических объектов. К ним относятся суточные, месячные, годовые и др. циклы.
Основными способами получения диагностической информации является анализ формы колебаний или их спектральный анализ. Информация о колебаниях в этом случае содержится в его периоде, частоте, амплитуде и фазе.
Примером может служить ЭКГ человека, в которой можно выделить ряд зубцов, несущих информацию о работе сердечно-сосудистой системы. Диагностическая информация содержится, прежде всего, в амплитудах разных зубцов ЭКГ и их соотношением.
Колебания интервалов между ударами сердца (R-Rинтервалов) или соответствующие колебаниям интервалов между пиками пульсовой волны используются для оценки работы системы регуляции человека.
