2.7. Скользящие режимы в релейных системах

Скользящим режимом называется режим работы релейной системы, характеризующийся колебательным движением изображающей точки вдоль линии переключения. Чем сильнее воздействие производной в цепи обратной связи, тем больше поворачиваются линии переключения реле против часовой стрелки. При этом интенсивность затухания переходного процесса возрастает. В том случае, когда в точке переключения угол наклона линии переключения становится равным наклону или меньше угла наклона касательной к фазовой траектории, по которой движется изображающая точка после переключения реле, возникают условия существования скользящего режима [10].

Рассмотрим возникновение скользящего режима в нелинейной системе, изображенной на рис. 2.20,а, с идеальным реле при отсутствии внешнего воздействия и при заданных начальных условиях x₀  0 и y₀ = 0.

Пусть начальное состояние системы задано точкой (x₀, 0) (рис. 2.25), от которой изображающая точка перемещается по фазовой траектории типа 1 до встречи с линией переключения AB в точке C. В этой точке происходит переключение реле и изображающая точка будет перемещаться по фазовой траектории типа 2 до точки D. В точке D происходит переключение реле в другую сторону, после чего изображающая точка будет перемещаться по фазовой траектории типа 1. Но как только увеличится результирующий сигнал обратной связи, произойдет переключение реле и изображающая точка будет перемещаться по фазовой траектории типа 2 и так далее, т.е. изображающая точка, подойдя к этому отрезку линии переключения - отрезку скольжения, не сможет уйти с него.

Таким образом, изображающая точка, достигнув точки D, непрерывно переходит с траектории типа 1 на траекторию типа 2 и обратно, как бы скользя вдоль линии переключения и асимптотически приближаясь к точке равновесия 0.

Как видно из рис. 2.25, скользящий режим возможен на тех участках, где фазовая траектория типа 2 проходит ниже линии переключения AB (после точки D). При начальном положении изображающей точки (x₀₂, 0) после ее прихода по траектории типа 1 в точку на линии переключения D сразу начинается скользящий режим. При начальном положении изображающей точки (x₀₃, 0) скользящий режим имеет место после переключения реле, когда изображающая точка скользит по линии переключения AB в четвертом квадранте. В последнем случае переходный процесс имеет перерегулирование.

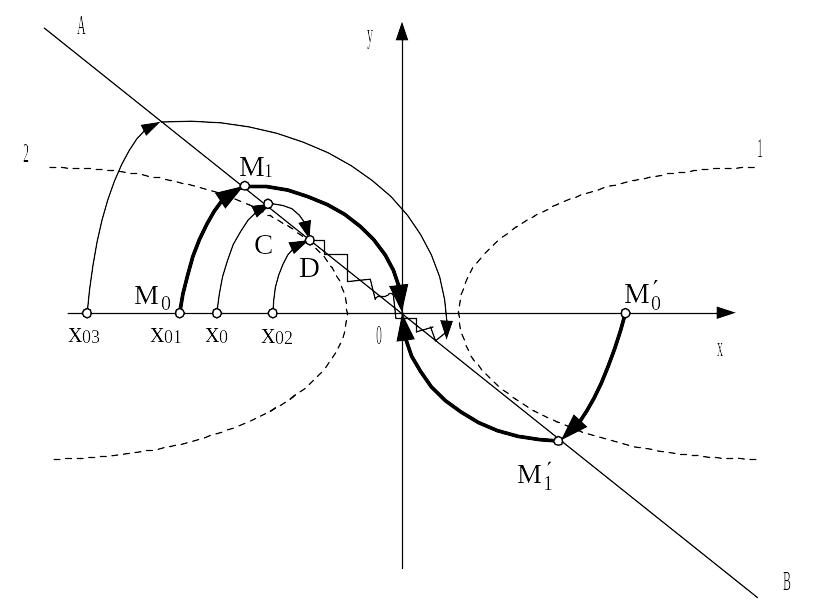
Рис. 2.25. Фазовые траектории релейной системы

В рассматриваемом примере предполагается, что переключение реле происходит мгновенно, в результате частота переключений бесконечно велика, а амплитуда колебаний бесконечно мала. Такой скользящий режим называется предельным. Если учесть неоднозначность характеристики или зону нечувствительности, то переключение реле при скользящем режиме происходит с конечной частотой, а амплитуда колебаний отличается от нуля.

В предельном скользящем режиме релейный элемент можно заменить эквивалентным линейным безынерционным звеном с коэффициентом передачи, стремящимся к бесконечности (k_p). Тогда эквивалентная передаточная функция системы, соответствующая структурной схеме, приведенной на рис. 2.20,а, будет

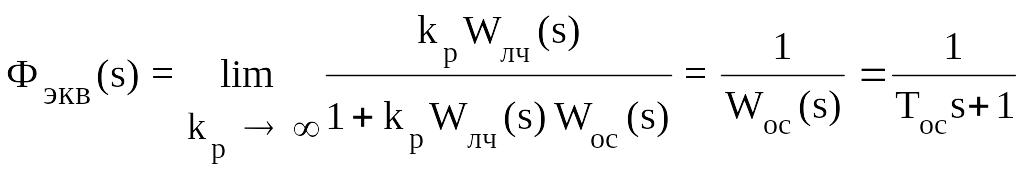. (2.73)

Следовательно, для предельного скользящего режима релейную систему можно представить эквивалентной структурной схемой в виде интегрирующего звена, охваченного обратной связью, или просто в виде апериодического звена первого порядка.

При начальном положении системы x₀₁ (точка M₀ на рис. 2.25) после переключения реле в точке M₁ изображающая точка по фазовой траектории типа 2 приходит в начало координат, характеризующее состояние покоя. При этом переходный процесс будет иметь минимальное время, а режим работы системы будет оптимальным по быстродействию. При заданной постоянной времени корректирующей цепи обратной связи T_oc такой режим будет существовать только для определенной группы начальных значений, когда изображающая точка в начальный момент времени оказывается на траектории M₀ M₁ 0 , проходящей через начало координат; во всех других случаях будет иметь место скользящий режим либо сразу после переключения реле, либо после нескольких переключений.

Для того чтобы процесс при любых начальных условиях был оптимальным по быстродействию, линией переключения должна быть сама фазовая траектория, проходящая через начало координат. Такая кривая линия переключения свидетельствует о нелинейном характере воздействия корректирующей обратной связи. Линия переключения не относится к фазовым траекториям. Но можно сделать так, что она будет совпадать с одной из фазовых траекторий. Тогда процесс в системе будет состоять из двух частей: подход к линии переключения по одной из траекторий, выбор которой зависит от начальных условий, и движение по линии переключения к положению равновесия.

Наглядное представление о совокупности оптимальных процессов при различных начальных условиях дает фазовый портрет, приведенный на рис. 2.26.

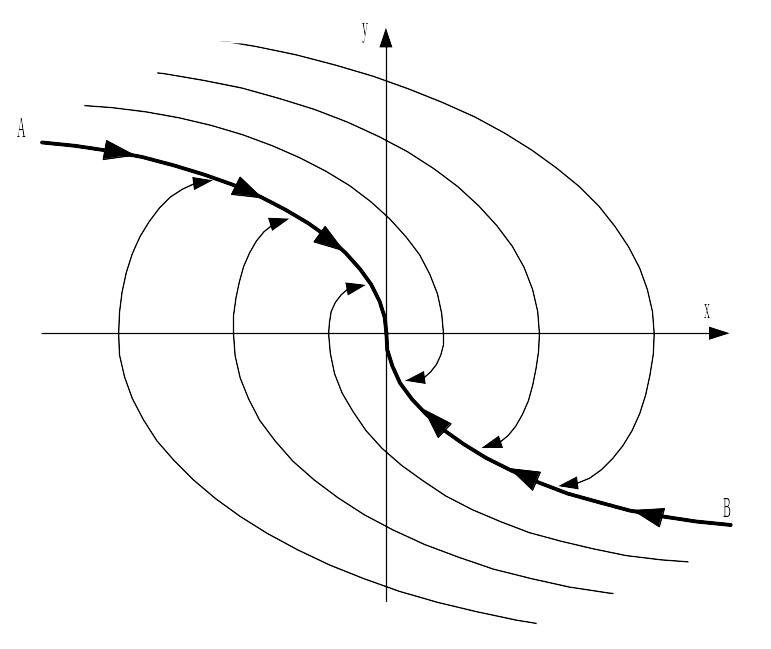
Рис. 2.26. Фазовый портрет оптимальной по быстродействию системы:

AB - линия переключения

При построении оптимальных по быстродействию систем основной задачей является формирование функции управления, характеризующей переключение релейного элемента. На рис. 2.27 приведена структурная схема системы с нелинейной обратной связью.

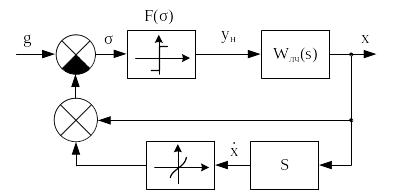
Рис. 2.27. Структурная схема оптимальной по быстродействию системы

В общем случае оптимальная по быстродействию система может содержать вычислительное устройство, формирующее функцию нелинейной обратной связи, логические элементы и иметь переменную структуру.