3 Отыскание условного экстремума при наличии нескольких

поверхностей отклика

На практике часто приходится отыскивать условный экстремум функции отклика при ограничениях, накладываемых другой функцией y₂=φ₂=(x₁, x₂,..x_k).

При большом числе независимых переменных задача решается методом неопределенных множителей Лагранжа.

Метод неопределенных множеств Лагранжа сводится к решению системы уравнений:

… (9)

относительно переменных х₁, х₂, ..x_k, λ при некотором фиксированном значении y₂.

Пример 3.

Для выхода реакции y₁ и чистоты продукта y₂ получены уравнения регрессии [1]:

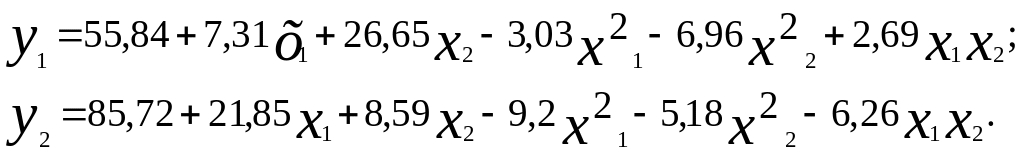
где – давление, – температура химического процесса.

Задавшись частотой продукта у₂=90%, находим условный экстремум для функции, определяющий выход реакции у₁.

Метод неопределенных множеств Лагранжа приводит к системе уравнений:

Методом скорейшего спуска были найдены три решения (табл. 1).

Таблица 1 – Результаты решения задачи на условный экстремум [1]

Варианты решений	1	2	3
	83,66	86,73	88,68
	94,87	92,47	89,99
	0,965	1,005	1,075
	1,088	1,316	1,479
λ	1,612	0,973	0,665

Анализ табличных данных показывает, что чистота продукта у₂ может быть достигнута за счет уменьшения выхода реакции у₁.

В ряде случаев при решении подобных задач сталкиваются со специфическими вычислительными трудностями, связанными с тем, что матрицы оказываются плохо обусловленными (определитель матрицы (X^тX) близок к нулю). Результаты вычислений при этом становятся неустойчивыми. Имеются ряд приемов, позволяющие преодолеть эти трудности [1].

Контрольные вопросы

1. Что нужно иметь для нахождения оптимальных условий функционирования системы и процессов?

2. Как выполняется крутое восхождение по поверхности отклика при поиске оптимальных условий функционирования систем?

3. Для чего приводятся уравнения регрессии к канонической форме?

4. Как проводится анализ уравнений в канонической форме?

5. Какие виды поверхностей отклика существуют и особенности их анализа?

6. Как отыскивается условный экстремум при наличии нескольких поверхностей отклика?

7. В чем сущность метода неопределенных множеств Лагранжа?

Лекция 4 Особенности планирования промышленного эксперимента

Промышленный объект исследования можно представить нижеприведенной схемой (рис.1). Независимые (факторные) переменные x₁⁰, x₂⁰, ..x_k⁰ регистрируются с погрешностью измерений e_i , i=1, 2, ..k. Зависимая переменная «y» «зашумлена» под влиянием неучтенных возмущающих воздействий d₁, d₂, ..d_s. Эквивалентный шум, приведенный к выходной переменной, представляет случайную величину, обозначен переменной «е».

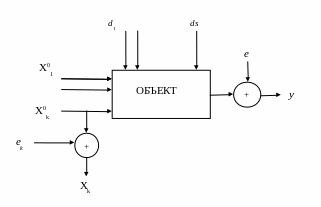
Рисунок 1 – Схема промышленного эксперимента по статистическому

описанию объекта в режиме нормального функционирования

Таким образом, при разработке модели регрессии, экспериментатор использует не точную информацию. Ниже рассматривается влияние погрешностей измерения входных и выходных переменных на точность коэффициентов регрессии и качество модели. Полагаем, что объект описывается линейной регрессионной моделью.

Допущения:

1) x_i, i=1, 2, ..k – нормально распределенный стационарный случайный процесс, обладает свойством эргодичности;

2) d₁- d_s – возмущающие воздействия, независимые случайные процессы с нулевым математическим ожиданием, среди которых нет доминирующих. Не коррелированны с входными переменными;

3) Объект исследования стационарный.

Выбор степени полинома возможно:

- с использованием априорной информации об объекте;

- выбор полинома 2-го и 3-го порядка и последовательный отсев незначимых коэффициентов.