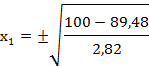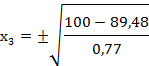2 Канонический анализ уравнения регрессии

Приведение уравнения к канонической форме и его анализ подробно излагается в курсе аналитической геометрии. Рассмотрим задачу с двумя независимыми переменными [1]:

² . (6)

В канонической форме (6) имеет вид:

(7)

Эта запись соответствует переносу начало координат в точку S и замене старых координатных осей х₁ и х₂ новыми осями Х₁ и Х₂, повернутыми на некоторый угол относительно старых осей. Y_s – значение выхода в новом начале координат S. Придавая Y некоторые фиксированные значения получаем контурные кривые равного выхода.

Возможны четыре типа контурных кривых: эллипсы, гиперболы, параллельные прямые, параболы.

Эллипсы: B₁₁ и B₂₂ имеют одинаковые знаки. Центр фигуры максимум, если коэффициенты отрицательны и минимум, если они положительные. Если B₂₂ по абсолютной величине меньше, чем B₁₁, то эллипс вытянут по оси Х₂. Поверхность отклика представляет собой эллиптический параболоид (рисунок 2).

Гиперболы: B₁₁ и B₂₂ имеют разные знаки. Если |B₁₁| < |B₂₂|, то контурные кривые вытянуты по оси X₂. Выход увеличивается при движении от центра S по одной оси и падает при движении вдоль второй оси. Центр фигуры - седло. Поверхность отклика представляет гиперболический параболоид. Попав в седловину исследователь изучает поверхность отклика в направлении осей Х₂ если его интересует максимум или оси Х₁, если его интересует минимум. Здесь, как и в методе крутого восхождения, намечаются мысленные опыты, и часть из них реализуется.

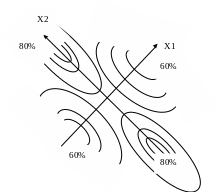
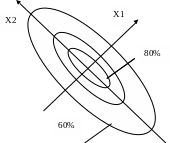
Эллипсы Гиперболы

Рисунок 2 – Кривые равного выхода поверхности отклика

(типа эллипса и гиперболы)

Параллельные кривые. Один из коэффициентов равен нулю B₂₂=0. Y_s – выход в любой точке на оси Х₂. Под определение центра фигуры попадает любая точка на оси Х₂. Поверхность отклика представляет стационарное возвышение (рис. 3).

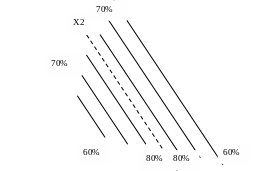
Рисунок 3 – Стационарное возвышение В₂₂=0, B₁₁<0.

Параболы. Один из коэффициентов равен нулю В₂₂=0, центр находится на бесконечности. Перенеся начало координат, в какую нибудь выбранную точку S^/ вблизи центра эксперимента, получаем уравнение параболы:

(8)

Центр находится в бесконечности, B₂ - крутизна наклона возвышения (рис. 4).

Практически возможны случаи, когда центр фигуры удален за перделы области, в которой варьировались переменные и один из коэффициентов В₁₁ или В₂₂ мало отличается от нуля [1]. В этом случае поверхность отклика, в зависимости от наклона возвышения, будет аппроксимироваться стационарным или возрастающим возвышением.

Условный экстремум в части факторного пространства, где проводиться эксперимент, может отыскиваться при ограничениях, накладываемых:

- сферой с центром в особой точке S;

- сферой с центром эксперимента;

- радиусом который задается точками планирования.

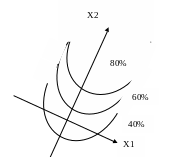
Рисунок 4 – Возрастающее возвышение, В₁₁<0, B₂₂=0, центр

в бесконечности.

Для отыскания условного экстремума в заданной области можно так же воспользоваться методом перебора всех комбинаций факторных переменных, квантуя переменные некоторым образом.

Пример 2.

Для описания поверхности отклика использовалось ротатабельное планирование второго порядка с величиной звездного плеча, равного α=2,0. Стационарная область описывалось уравнением регрессии:

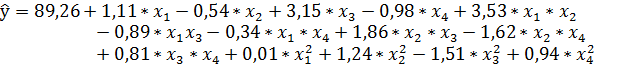
Была найдена каноническая форма уравнения:

Центр фигуры S имеет координаты:

.

попадающие в область варьирования факторных переменных. Зависимая переменная в центре новых координат S имеет величину .

Переход от старых координат к новым задается соотношениями:

Исследуемая поверхность отклика относиться к типу «минимакса»: при движении в направлении новых осей Х₁ и Х₃ переменная У увеличивается, а в направлении Х₂ и Х₄ – уменьшается.

Для поиска максимума y=100% надо «выползать» из точки S, двигаясь вдоль Для нахождения координат: это четырех точек нужно решить системы уравнений:

Проводя восхождение, находим точки локального экстремума:

Подставляя координаты этих точек в исходное уравнение регрессии, находятся выходы 100.32%; 100,73%; 99,78%; 100,78%. Из четырех точек только одна оказалась далеко удаленной от области факторного пространства, в которой производились эксперименты.