Задача состоит в том, чтобы получить разбиение, которое минимизирует функцию:

, (5)

где С (Ei) – функция, определенная на множестве разбиений Ei , i = 1, 2.,. N

Задача синтеза функциональной структуры системы состоит в разбиении Е на подмножества Е₁, Е₂….. ,Е_N при различных критериях разбиения системы на подсистемы. При этом близость операции e_i к e_j будем характеризовать величиной m_ij, где m_ij – значение потока по дуге h_ij графа Г, измеряемое объемом информации или количеством связей.

Можно выделить два принципа декомпозиции:

1. разложение переменных;

2. разложение ограничений.

Если дуга (e_i, V_k) разрывается и то в первом случае (разложение переменных) вместо вершины е_i вводятся две несвязанными между собой: вершина е_i^’ и е_i^’’. При этом вершина е_i^’ остается связанной только с вершинами первой подсистемы, а вершина е_i^’’ – с вершинами второй подсистемой. Это преобразование соответствует тому, что в целевой функции и ограничениях первой подсистемы x_i заменяется на x_i^/. а во второй на x_i^.//. Благодаря этому модели подсистем становятся формально независимыми и необходимым (а иногда достаточным) условием согласования является выполнение равенства:

х^’ = x^’’.

Разложение систем на несколько относительно автономных подсистем приводит к необходимости создания высшего координирующего органа. Формальными способами воздействия координирующего органа могут служить: плата за взаимодействие, фиксирование взаимодействий, оценки и предсказания взаимодействий.

В методе разложения ограничений вместо вершины V_k вводится две вершины: V_k^’ и V_k^’’, первая из которых связана только с первой подсистемой, а вторая – только со второй подсистемой. Это соответствует тому, что вместо одного ограничения

на ресурсы типа k вводят два несвязанных ограничения:

,

где U_k , U_k^’ , U_k^’’ – количество ресурсы соответственно V_k ,V_k’ и V_k^’’.

Здесь необходимо выполнение условия U_k = U_k^’ + U_k^’’.

Формальным способом воздействия координирующего органа на подсистемы в этом случае может служить распределение ресурсов и платы за ресурсы.

Таким образом, после решения задачи разбиения системы на подсистемы с помощью двух рассмотренных принципов декомпозиции проводится разрыв связей и выбор способов координации.

Не уменьшая общности дальнейших рассуждений, рассмотрим матричную модель системы, полученную из Г² и описываемую системой линейных ограничений:

Ах≤u; x≥0, (6)

где А – матрица; x и u векторы столбцы с критерием

cx→max; (7)

здесь с – вектор строка.

Рассмотрим квазиблочную матрицу:

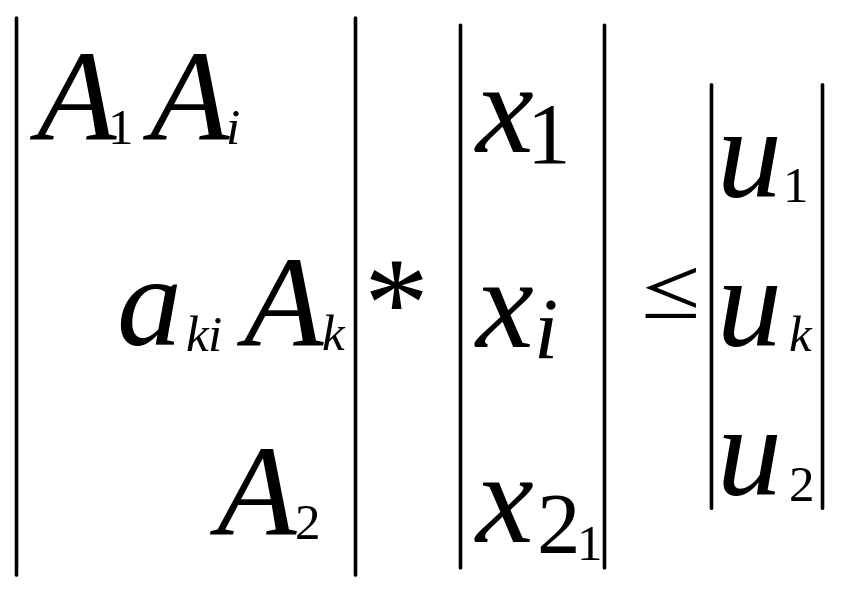(8)

где А₁ и А₂ подматрицы матрицы А ;

х₁, х₂, u₁, u₂ –вектор столбцы;

А_к – вектор строка.

Для того, чтобы матрица А распалась на две независимые подматрицы (подсистемы), можно воспользоваться одним из методов декомпозиции, рассмотренных выше. Если целесообразно объединить подразделение минимизируемой структуры в соответствии с типом используемых им ресурсов (т.е. по функциональному признаку), то применяется разложение переменных x_i на x_i^/ и x_i^//. Получаются две независимые подсистемы: первая оптимизирует x₁ и x_i^/ при ограничениях

, (9)

вторая – x₂ и x_i^// при ограничениях

(10)

Координирующий орган воздействует на подсистемы таким образом, чтобы

x_i^/-x_i^//→0 . (11)

В общем случае производится разложение графа Г по переменным u₁ и u₂.

Возможно другое разделение матрицы, при котором подразделения объединяют в соответствии с содержанием работ (по тематическому признаку). В этом случае образуются независимые подсистемы: первая оптимизирует x₁, x_i при ограничениях

(12)

Вторая – х₂ при ограничениях

(13)

Координирующий орган регулирует значения u_k^/, u_k^// таким образом, чтобы решения, полученные подсистемами, были оптимальны для организации в целом, и выполнялось условие

u_k^/+u_k^//=u_k.

В общем случае проводится разложение графа Г по ресурсным вершинам.

Иллюстрацией модели системы (6), (7) может служить управляющий орган, выполняющий функции планирования, формализуемую в виде задачи линейного программирования, имеющую матрицу условий рассматриваемого вида, например задач планирования выпуска продукции предприятием. При этом обозначения интерпретируются следующим образом:

вектор x – выпуск продукции ( x_i – выпуск продукции i-го вида);

А- матрица затрат сырья (a_ki – затраты сырья k-го вида на выпуск единицы продукции i-го вида);

с- вектор стоимостей или прибыли; u – вектор наличия сырья.

Особенность матрицы (два блока с зацеплением по i-му виду продукции) позволяют провести декомпозицию задачи на две задачи линейного программирования, которые соответствуют двум элементам организационной структуры (плановые отделы) по двум группам продукции и координирующего органа. После разбиения множества функций АСУ на подсистемы и задачи возникает необходимость распределения задач по узлам и уровням организационной структуры АСУ.

При определении оптимального распределения функций по узлам АСУ исходными являются:

1). Выполняемые системой функции, формализованные в виде множества решаемых задач, каждая из которых состоит из ряда этапов;

2). Связи между задачами и их этапами.

3). Множество возможных узлов АСУ и связей между ними.

4). Виды и характеристики технических средств, применение которых возможно в проектируемой системе.

5). Внешние для системы источники и потребности информации по всем задачам и их этапам.

Задача выбора оптимальной структуры ставится как нелинейная задача математического программирования:

F₀(x_ijkl)→extr;

F_n(x_ijkl)≤B_n n=1, 2, ..m;

(i=1, 2, ..n). (14)

x_ijkl – булевая переменная, равная единице, если функциональная задача i решается в j-м узле системы с помощью алгоритма k на l-м наборе технических средств, и равна нулю в противном случае.

Эффективность выбранной структуры должна базироваться на обоснованном соотношении величины выгод (затрат) и сроков их получения. Эффект от внедрения АСУ складывается из различных факторов, одни из которых представляют интерес для организации, непосредственно внедряющей систему, другие имеют общее народнохозяйственное значение (для региона, государства), и результаты их реализации на деятельность организации отражаются косвенным образом.

Модель позволяет учитывать такие характеристики эффективности вариантов структуры системы, как стоимость, оперативность, надежность и др.

Разработанные методы дают решение задачи синтеза структуры АСУ в случае аддитивных мультипликативных функций. Оптимальную структуру определяют при ограничениях на ресурсы, загрузку ТС, на своевременное решение задач и их этапов и т.д.