
4437
.pdfББК У9 (2) 26 Х12
Введение в финансовую математику : методические указания для выполнения контрольной работы для бакалаврантов 2–3-го курсов направления «Экономика» профилей «Страхование», «Финансы и кредит», «Налоги и налогообложение» заочной формы обучения / сост. д-р экон. наук, доцент М. Ю. Серкин. – Хабаровск : РИЦ ХГАЭП, 2011.– 32 с.
Рецензент
С. Н. Леонов, заместитель директора по науке
Института экономических исследований
ДВО РАН
доктор экономических наук, профессор
Утверждено издательско-библио- течным советом академии в качестве методических указаний
©Серкин Максим Юрьевич, 2011
©Хабаровская государственная академия экономики и права, 2011
2
ВВЕДЕНИЕ
Курс "Введение в финансовую математику" знакомит студентов с ос-
новными положениями теории процентных ставок в объёме, который принят в аналогичных учебных заведениях стран Запада.
В процессе изучения курса студент знакомится с кругом задач данной области (ренты, аннуитеты, кредитные расчёты, анализ инвестиционных проектов, ценных бумаг), которые практикуются в странах с рыночной экономикой. При этом следует иметь в виду, что наряду со знакомыми и достаточно простыми понятиями (простые, сложные проценты и др.)
появятся новые и непростые понятия, такие как "сила процента", "дискретные и непрерывные потоки наличности", "уравнение стоимости".
В этих новых терминах будут использоваться математические понятия производной и интеграла. Этого не следует бояться, так как в процессе выполнения заданий будут встречаться только интегралы, имеющиеся в таблицах интегралов любого учебника по высшей математике.
Знания, полученные при изучении дисциплины «Введение в финансовую математику», будут использоваться при анализе случайных потоков наличности, страховых рент и страхования жизни, оценки риска.
Методические указания содержат программу курса "Введение в финансовую математику", задания к контрольным работам и методические указания по их выполнению, а также список литературы, в которой излагаются соответствующие вопросы.
Методические указания включают общие положения и порядок выполнения заданий, содержат необходимые определения, формулы,
анализ их применения к решению задач контрольной работы. Каждая тема снабжена решением типовых примеров.
3
1.1. ТЕМАТИЧЕСКИЙ ПЛАН
Тема 1. ПРОСТЫЕ ПРОЦЕНТЫ План
1.Определение простых процентов.
2.Текущая стоимость.
3.Простой дисконт.
Тема 2. СЛОЖНЫЕ ПРОЦЕНТЫ План
1.Понятие сложных процентов.
2.Номинальные процентные ставки.
3.Коэффициенты накопления.
4.Принцип согласованности.
Тема 3. СИЛА ПРОЦЕНТА План
1.Определение силы процента.
2.Связь между силой процента и коэффициентом накопления.
3.Связь между номинальными процентными ставками и силой процента.
4.Текущая стоимость.
5.Формула Студли.
Тема 4. ПОТОКИ НАЛИЧНОСТИ План
1.Дискретные и непрерывные потоки наличности.
2.Текущая стоимость потока наличности.
3.Оценка текущей стоимости потока наличности.
4.Процентный доход.
Тема 5. УРАВНЕНИЕ СТОИМОСТИ План
1.Уравнение стоимости для дискретного и непрерывного потоков наличности.
2.Внутренняя норма прибыли или доходность сделки.
3.Условия существования доходности сделки.
4
1.2. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Бадюков В. Ф. Финансовая математика : учеб . пособие / В. Ф. Бадюков, С. Ю. Серкин. – Хабаровск : ХГАЭП, 2009.
2. Капитоненко В. В. Задачи и тесты по финансовой математике : учеб. пособие / В. В. Капитоненко. – М. : Финансы и статистика, 2007.
3.Кузнецов Б. Т. Финансовая математика : учеб. пособие для вузов / Б. Т. Кузнецов. – М. : ЭКЗАМЕН, 2005.
4.Лукашин Ю. Ф. Финансовая математика : учеб. пособие / Ю. Ф. Лукашин. – М., 2004.
5. Соловьёв А. К. Актуарные расчёты а пенсионном страховании / А. К. Соловьёв. – М. : Финансы и статистика, 2006.
6. Шапкин А. С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. / А. С. Шапкин. – 3-е изд. – М. : Дашков и Ко, 2009.
2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
2.1. ОБЩИЕ ПОЛОЖЕНИЯ Согласно учебному плану каждый студент обязан выполнить
контрольную работу, показав степень усвоения основных тем курса. Сту-
дент, правильно выполнивший контрольную работу, получает оценку
"зачтено" и допускается к экзамену, а получивший оценку "не зачтено"
вносит исправления согласно замечаниям преподавателя, рецензирующего
работу.
Варианты контрольной работы определяются по последней цифре
номера зачётной книжки. Если номер заканчивается на цифру "0", то
номер варианта – 10.
Каждый вариант предусматривает выполнение шести заданий:
-простые проценты (два задания);
-сложные проценты;
5
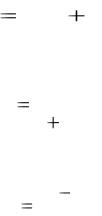
-сила процента и соотношения между процентными ставками;
-потоки наличности;
-уравнение стоимости.
Сначала в тетрадь переписывается задание, затем приводится решение. Последовательность внесения решения задач в контрольную работу регламентируется от первой до последней по порядку. В завершение контрольной работы должен быть приведён список использованной литературы.
2.2. Теоретические положения и решение |
типовых заданий |
контрольной работы
2.2.1. Простые проценты
Для решения задач на эту тему необходимо знать следующие расчётные
формулы:
A P(1 it), |
(1.1) |
P |
|
|
A |
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
it , |
|
(1.2) |
|||||
|
|
|||||||
i |
|
|
A |
P |
|
|
||
|
|
|
|
|
|
. |
(1.3) |
|
|
|
|
pt |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
В формуле (1.1) A – накопленная стоимость, P – начальная стоимость, i – простая процентная ставка, t – период времени. В формуле (1.2)
начальная стоимость носит название текущей или дисконтированной стоимости накопленной стоимости A . В формулах типа (1.1) – (1.3)
отражается в простейшем случае весь круг задач финансовой математики,
когда одна из величин выражается через три остальные. При
использовании формул (1.1) – (1.3) следует помнить о соответствии единиц измерения величин i и t .
6
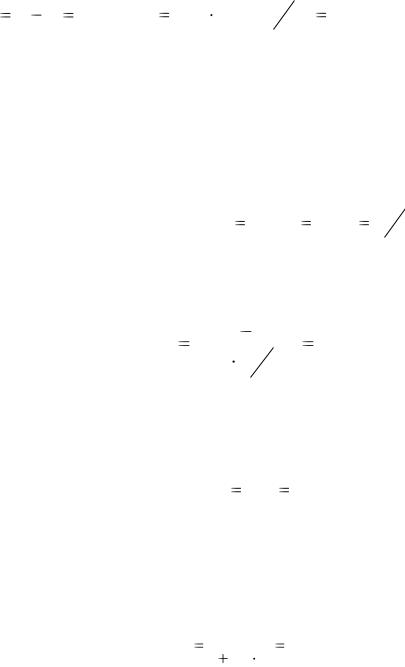
Пример 1.1. Найти сумму процентов по кредиту 1 000 у. д. е. (условных
денежных единиц) на 36 дней при простой процентной ставке 8 % в год.
Решение: Исходя из экономического смысла задачи сумма процентов
S находится по формуле
S A P iPt, т.е. S 0,08 1000 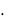 35365 7,67 (у. д. е.)
35365 7,67 (у. д. е.)
При решении этой задачи следует иметь в виду, что в финансовом
исчислении Запада расчётный год состоит из 365 дней, если не указано:
високосный год или нет.
Пример 1.2. Кредит 130 у. д. е. погашается суммой 150 у. д. е. за 25
дней. Найти простую полугодовую процентную ставку.
Решение: В данной задаче P |
130, A 150,t |
25 |
365. |
Тогда простая |
||||
|
||||||||
|
|
|
|
|
|
|
|
|
годовая процентная ставка находится по формуле (1.3): |
|
|
||||||
io |
150 |
130 |
|
2,25. |
|
|
|
|
|
|
|
|
|
|
|
||
130 |
25 |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
365 |
|
|
|
|
|
Полугодовая процентная ставка
i |
1 |
i0 1,12 . |
|
2 |
|||
|
|
Пример 1.3. Найти текущую стоимость суммы 250 у. д. е.,
выплачиваемой через 2 года при простой процентной ставке 10% в год.
Решение: Исходя из формулы (1.2)
P |
|
250 |
|
208,33. |
|
|
|
||
|
|
|
||
1 |
0,1 |
2 |
|
|
Наряду с простой процентной ставкой, определяемой формулой (1.3), в
финансовом исчислении используется простая дисконтная ставка или учётная ставка, определяемая формулой
7
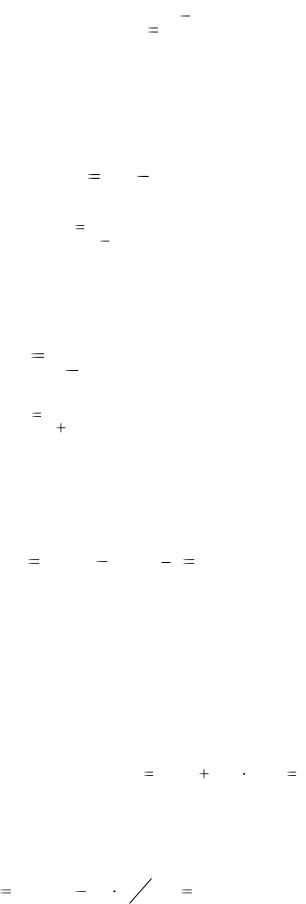
d |
A P |
|
|
|
|
. |
(1.4) |
||
At |
||||
|
||||
|
|
|
В терминах учётной ставки текущая и накопленная стоимости связаны соотношениями
|
|
|
P |
|
|
A(1 dt), |
(1.5) |
||
|
|
|
A |
|
|
P |
. |
(1.6) |
|
|
|
|
|
|
|
||||
|
1 dt |
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Связь между учётной и процентной ставками в единицу времени |
|||||||||
даётся формулами |
|
|
|
|
|
||||
i |
|
|
d |
|
|
|
, |
(1.7) |
|
|
|
|
|
|
|
|
|||
1 |
|
d |
|
||||||
|
|
|
|
|
|||||
d |
|
|
i |
. |
|
|
(1.8) |
||
|
|
|
|
|
|
||||
1 i |
|
|
|||||||
|
|
|
|
|
|
||||
Пример 1.4. Дисконтировать 200 у. д. е. на 4 месяца при простой учётной ставке 7 % в год.
Решение: Согласно формуле (1.5)
P 200(1 0,07  13 ) 195,33.
13 ) 195,33.
Пример 1.5. Вексель с номинальной стоимостью 200 у. д. е. под 12 %
годовых сроком на 70 дней продаётся банку с учётной ставкой 10 %
годовых через 30 дней после подписания векселя. Найти а) цену продажи;
б) норму прибыли (в год) продавца; в) норму прибыли (в год) банка.
Решение: Найдём фактическую стоимость векселя по формуле (1.1):
|
A |
200(1 0,12 |
70 |
) 204,6 . |
|
|
|
||||
|
|
|
365 |
|
|
Чтобы найти цену продажи, необходимо дисконтировать факти- |
|||||
ческую стоимость A |
по формуле (1.5): |
|
|||
P 204,6(1 |
0,1 40 |
365 |
) 202,36. |
|
|
|
|
|
|
|
|
Норма прибыли, как известно, находится по формуле |
|||||
8
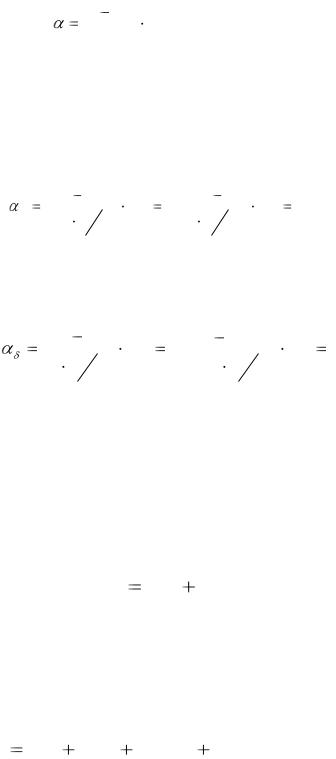
|
C Co |
100(%), |
(1.9) |
|
Cot |
||
|
|
||
|
|
|
|
где Co – начальная сумма; C – накопленная сумма, t – время |
|||
накопления. Тогда норма прибыли продавца |
|
||
n |
P1 |
200 |
100 |
202,36 200 |
100 14,34(%). |
||
200 |
30 |
200 |
30 |
||||
|
|
||||||
|
|
|
|||||
|
|
365 |
|
|
365 |
|
|
Норма прибыли банка
|
A P1 |
100 |
204,6 |
202,36 |
100 10,1(%). |
|
P |
40 |
202,36 |
40 |
|||
|
|
|||||
1 |
365 |
|
|
365 |
|
|
|
|
|
|
|
2.2. Сложные проценты Сложные проценты отличаются от простых, как известно, тем, что при
простой процентной ставке i в единицу времени накопление за n
единиц времени находится по формуле
A P(1 i)n . |
(2.1) |
Если простые процентные ставки в различные единицы времени
различны: i1 , i2 ,..., in |
то накопление за |
n единиц времени находится по |
формуле |
|
|
A P(1 i1 )(1 |
i2 )...(1 in ). |
(2.2) |
Формулы (2.1) и (2.2) описывают круг задач на сложные проценты,
то есть одна из величин находится, если заданы остальные. При этом дисконтирующий множитель V (n) имеет вид:
9

|
|
|
|
V (n) |
|
1 |
V n |
, |
|
|
|
|
|
|
|
||||
|
|
|
|
|
i)n |
||||
|
|
|
|
(1 |
|
|
|||
где |
V |
1 |
–- дисконтирующий множитель за 1единицу времени. |
||||||
|
|
||||||||
1 i |
|||||||||
|
|||||||||
Пример 2.1. Фактическая простая процентная ставка на настоящее время составляет 12 % в год, но через 2 года она понизится до 5 % в год.
Найти накопление вклада 2 000 у. д. е. за 4 года.
Решение: Согласно формуле (2.2)
A |
2 000 (1 |
0,12)2 |
(1 |
0,05)2 |
2 765,95. |
Иногда в реальной практике деловой жизни используются так
называемые номинальные процентные ставки в единицу времени ih (t) на срок h от момента времени t . Величина ih (t) определяется так, что
фактическая простая процентная ставка на срок |
h равна h ih (t) , то есть |
A P(1 h ih (t)), |
(2.3) |
где P – начальный капитал; A – накопленный капитал.
Пример 2.2. Номинальная годовая процентная ставка на срок 3 дня
равна 10,8 % Найти накопление капитала 1 000 у. д. е.
Решение: По формуле (2.3) находим
A |
1 000 (1 |
3365 |
0,108) |
1 000,89. |
Определим коэффициент накопления. Для t2 t1 под величиной
A(t1,t2 ) (коэффициент накопления) будем понимать накопленную
стоимость единичной суммы за время t |
2 |
t |
от момента t |
1 |
. |
|||
|
|
|
|
1 |
|
|
||
Из определения |
A(t ,t |
2 |
) и i (t) следуют формулы |
|
|
|||
|
1 |
h |
|
|
|
|
|
|
10
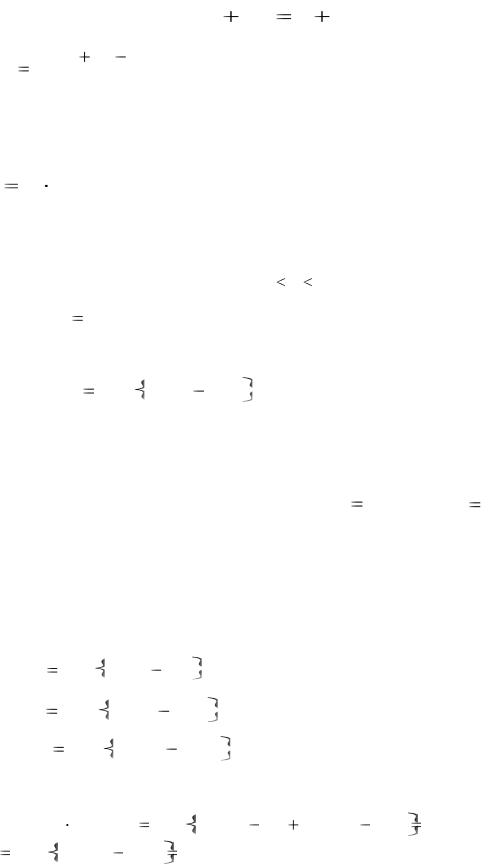
A(t, t h) 1 h  ih (t) ,
ih (t) ,
ih (t) |
A(t,t |
|
h) 1 |
|
|
|
|
. |
|
|
h |
|
||
|
|
|
|
|
Накопление капитала P находится по формуле
A P A(t1,t2 ). |
(2.4) |
При нормально функционирующей экономике выполняется принцип
согласованности, определяемый при to t1 t2 тождеством
A(t0 , t2 ) A(t0 , t1)  A(t1, t2 ).
A(t1, t2 ).
Пример 2.3. Коэффициент накопления определяется формулой
A(t1,t2 ) exp 0,09(t2 |
t1) |
|
||
в единицу времени – 1 год. |
|
|||
Найти: |
|
|
|
|
а) накопление суммы 250 у. д. е. от момента t |
3 на срок h 3 |
|||
(месяц); |
|
|
|
|
б) проверить принцип согласованности. |
|
|||
Решение: а) по формуле (2.4) находим |
|
|||
A(t0 , t1 ) |
exp 0,09(t1 |
t0 ) , |
(2.5) |
|
A(t1,t2 ) |
exp 0,09(t2 |
t1) |
, |
(2.6) |
A(t0 , t2 ) |
exp 0,09(t2 |
t0 ) . |
(2.7) |
|
Перемножая (2.5) и (2.6), получим |
|
|||
A(t0 , t1 ) A(t1, t2 ) exp |
0,09(t1 t0 ) 0,09(t2 |
t1 ) |
||
exp |
0,09(t2 t0 ) |
A(t0 , t2 ). |
|
|
11
