
4434
.pdfМинистерство образования Российской Федерации
Хабаровская государственная академия экономики и права
Кафедра математики и математических методов в экономике
Экономико-математические методы и модели
Методические указания и контрольные задания для студентов 3 курса специальности 062000 “Антикризисное управление” дневной и заочной форм обучения
Хабаровск 2003
2
В
Х 12
Экономико-математические методы и модели: Методические указания и контрольные задания для студентов 3 курса специальности 062000 “Антикризисное управление”, дневной и заочной формы обучения/ Сост. Т.В. Ракова.-Хабаровск: РИЦ ХГАЭП, 2003. – 24 с.
Рецензент: к.э.н. доцент завкафедрой экономической кибернетики ХГТУ К.Т. Пазюк
Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов
Ракова Татьяна Валерьевна
Экономико-математические методы и модели
Редактор Г.С. Одинцова
___________________________________________________________________________
Подписано в печать_____________. |
Формат 60х84/16. |
Бумага писчая |
|
Печать офсетная. |
Усл. п.л. 1,4 |
Уч.-изд.л.1,2 |
Тираж 100 экз. |
Заказ №_____ |
|
|
|
___________________________________________________________________________
680042, г. Хабаровск, ул. Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2003
3
Введение
Экономико-математические методы и модели – это научная дисциплина, имеющая важное методологическое значение в системе подготовки современного экономиста.
Методические указания разработаны для выполнения контрольных работ студентами 3 курса специальности 062000 “Антикризисное управление” дневной и заочной форм обучения.
Вметодических указаниях представлены следующие темы: “Теория игр”, “Динамическое программирование”, “Теория массового обслуживания” и “Планирование и управление запасами”.
Задача теории игр определяет оптимальные пропорции в выпускаемой продукции, гарантирующие прибыль, при любом состоянии спроса.
Задачи динамического программирования сводятся к нахождению оптимального распределения капитальных вложений между отраслями и оптимизации прибыли от эксплуатации оборудования.
Задачи массового обслуживания посвящены изучению и анализу систем обслуживания с очередями заявок или требований и состоят в определении показателей эффективности работы систем, их оптимальных характеристик.
Задачи планирования и управления запасами состоят в отыскивании оптимальных значений уровня запасов и размера заказа. Особенность таких задач заключается в том, что с увеличением уровня запасов, с одной стороны, увеличиваются затраты на их хранение, но с другой стороны, уменьшаются потери вследствие возможного дефицита запасаемого продукта.
Вметодических указаниях приводятся большое количество экономических задач с решением и задания для самостоятельного выполнения контрольных работ.
Вариант для контрольного задания выбирается в соответствии с последней цифрой зачетки (0 соответствует 10 варианту).

4
1. Теория игр
На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т.е. возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Такие ситуации, возникающие при игре, относятся к конфликтным: результат каждого хода зависит от ответного хода противника. Цель игры – выигрыш одного из партнеров.
Рассмотрим основные понятия теории игр. Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, - игроками, а исход конфликта – выигрышем. Для каждой формализованной игры вводятся правила, т.е. система условий, определяющая варианты действий игроков, объем информации каждого игрока о поведении партнеров, выигрыш, к которому приводит каждая совокупность действий.
Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Рассмотрим парные игры. В них участвуют два игрока А и В, интересы которых противоположны, а под игрой будем понимать ряд действий со стороны А и В.
Игра называется игрой с нулевой суммой, или антогонистической, если выигрыш одного из игроков равен проигрышу другого. Если а – выигрыш одного из игроков, b – выигрыш другого, то для игры с нулевой суммой b  a .
a .
Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход – это сознательный выбор игроком одного из возможных действий. Случайный ход – это случайно выбранное действие.
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от конкретной ситуации. Игра называется конечной, если у каждого игрока имеется конечное число стратегий, и бесконечной – в противном случае.
Для того чтобы решить игру или найти решение игры, следует каждому игроку выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Оптимальные стратегии должны также удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре.
Пример 1. Предприятие может выпускать три вида продукции (А1, А2 и А3), получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний (В1, В2, В3 и В4). Дана матрица (табл.1.1), элементы которой aij
характеризуют прибыль, которую получит предприятие при выпуске i-ой продукции с j-ым состоянием спроса.
|
|
|
|
|
Таблица 1.1 |
|
Матрица платежей |
|
|
|
|
||
|
|
В1 |
В2 |
В3 |
|
В4 |
|
А1 |
4 |
4 |
2 |
|
6 |
|
А2 |
9 |
9 |
6 |
|
3 |
|
А3 |
9 |
10 |
8 |
|
4 |
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.

5
Решение. Попытаемся упростить платежную матрицу, для чего отбросим стратегии заведомо невыгодные или дублирующие. Так, вторая стратегия (второй столбец матрицы) является невыгодной для игрока В по сравнению с первой (элементы второго столбца больше элементов первого столбца), так как цель игрока В – уменьшить выигрыш игрока А. Поэтому второй столбец можно отбросить. Получаем матрицу Р размера 3 3 :
4 2 6 P 9 6 3 .
9 8 6
Определим нижнюю и верхнюю цены игры в табл. 1.2. Таблица 1.2
Вспомогательные расчеты
Cпрос
Вид |
В1 |
В2 |
В3 |
ai |
|
|
|
|
|
продукции |
|
|
|
|
А1 |
4 |
2 |
6 |
2 |
А2 |
9 |
6 |
3 |
3 |
А3 |
9 |
8 |
4 |
4 |
j |
9 |
8 |
6 |
4 |
|
|
|
6 |
|
|
|
|
|
Нижняя цена игры – это гарантированный максимальный выигрыш игрока А при
любой стратегии игрока В. Нижняя цена игры рассчитывается по формуле |
|
max min aij |
(1.1) |
i 1,...,m j 1,...,n |
|
Верхняя цена игры – это гарантированный минимальный проигрыш игрока В при любой стратегии игрока А. Верхняя цена игры рассчитывается по формуле
|
|
|
|
|
|
|
|
|
min max aij |
(1.2) |
||
|
|
|
|
|
|
|
|
|
j |
1,...,n i 1,...m |
|
|
|
Следовательно, |
|
4 и |
6 . |
Так как |
|
, то седловая точка отсутствует и |
|||||
оптимальное |
решение |
следует |
искать |
в смешанных стратегиях игроков: |
||||||||
S * |
( p , p |
2 |
, p ) и |
S * |
(q , q |
2 |
, q ) . |
|
|
|
|
|
A |
1 |
|
3 |
B |
1 |
3 |
|
|
|
|
||
|
Для оптимальной стратегии S A* все средние выигрыши не меньше цены игры , |
|||||||||||
поэтому получаем первую систему неравенств: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4 p1 |
9 p2 |
9 p3 |
, |
|
|
|
|
|
|
|
|
|
2 p1 |
6 p2 |
8 p3 |
, |
|
|
|
|
|
|
|
|
|
6 p1 |
3 p2 |
6 p3 |
, |
pi 0, i 1,2,3
p1 p2 p3 1.
Каждое из неравенств разделим на число  0 . Введем новые переменные, используя формулу
0 . Введем новые переменные, используя формулу
xi pi / . |
(1.3) |
Получим x1 p1 / , x2 p2 / , x3 p3 / . Тогда система изменится следующим образом:
. Тогда система изменится следующим образом:

|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x1 |
9x2 |
9x3 |
1, |
|
|
|
|
|
|
|
|
|
||||||
|
2x1 |
6x2 |
8x3 |
1, |
|
|
|
|
|
|
|
|
|
||||||
|
6x1 |
|
3x2 |
6x3 |
1, |
|
|
|
|
|
|
|
|
|
|||||
p j |
0, |
j |
1,2,3 |
|
|
|
|
|
|
|
|
|
|
||||||
Z |
x1 |
|
x2 |
x3 |
1 |
|
|
|
min . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для оптимальной стратегии |
S * |
все средние выигрыши не больше цены игры , |
|||||||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому получаем вторую систему неравенств: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4q1 |
2q2 |
6q3 |
, |
|
|
|
|
|
|
||||||||
|
|
9q1 |
6q2 |
3q3 |
, |
|
|
|
|
|
|
||||||||
|
|
9q1 |
8q2 |
4q3 |
, |
|
|
|
|
|
|
||||||||
|
q j |
|
0, |
j |
1,2,3 |
|
|
|
|
|
|
|
|||||||
|
q1 |
|
q2 |
q3 |
1. |
|
|
|
|
|
|
|
|
|
|
||||
Каждое из неравенств разделим на число |
0 . |
|
|
|
|
|
|
|
|
|
|||||||||
Введем новые переменные, используя формулу |
|
|
|
|
|
|
|
||||||||||||
|
y j |
|
q j / . |
|
|
|
|
|
|
|
|
|
|
|
(1.4) |
||||
Получим y1 q1 / , y2 q2 / |
, |
y3 |
|
q3 / . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда система изменится следующим образом: |
|
|
|
|
|
|
|
||||||||||||
|
4 y1 |
|
2 y2 |
6 y3 |
1, |
|
|
|
|
|
|
|
|
||||||
|
9 y1 |
|
6 y2 |
3y3 |
1, |
|
|
|
|
|
|
|
|
|
|||||
|
9 y1 |
|
8 y2 |
4 y3 |
1, |
|
|
|
|
|
|
|
|
|
|||||
y j |
0, |
j |
1,2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
W |
y1 |
y2 |
y3 |
1 |
|
max |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Переменные уj (j = 1,2,3) удовлетворяют условию: y |
y |
|
y |
|
. |
||||||||||||||
2 |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Решаем симплексным методом одну из задач, например задачу 2. |
|||||||||||||||||||
Введем балансовые переменные и перейдем к уравнениям: |
|
|
|
|
|||||||||||||||
|
4 y1 |
|
2 y2 |
6 y3 |
|
|
y4 |
1, |
|
|
|
|
|
|
|||||
|
9 y1 |
|
6 y2 |
3y3 |
|
y5 |
1, |
|
|
|
|
|
|
||||||
|
9 y1 |
|
8 y2 |
4 y3 |
|
y6 |
1, |
|
|
|
|
|
|
||||||
y j |
0, |
|
y j |
1,...,6 |
|
|
|
|
|
|
|
|
|
||||||
W |
y1 |
|
y2 |
y3 |
1 |
|
|
max . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Получим оптимальное решение задачи 2: Y * |
|
|
|
(0,1;0;0,1;0,3;0;0) и W 0,2 . |
|||||||||||||||
Определим оптимальное базисное решение задачи 1 с помощью теории двойственности. Установим соответствие между переменными взаимно-двойственных задач:
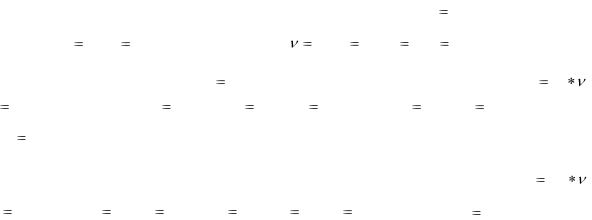
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
x4 |
|
x5 |
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y4 y5 |
y6 |
y1 |
|
y2 |
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Получим |
|
оптимальное |
|
решение |
задачи |
1: |
|
X * |
(0;0,05;0,15;0;0,25;0) , |
|||||||||||||||||
причем Z * |
W * |
0,2. |
Из соотношения |
|
1 |
|
1 |
|
1 |
5 . |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Z * |
W * |
|
|
|
|
|
|
||||||||||||||||||
|
|
min |
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
max |
|
|
|
|
|
|
|
||
|
Оптимальную стратегию S |
* |
( p , p |
2 |
, p ) |
находим, используя формулу p* |
x |
i |
, |
||||||||||||||||||
|
|
|
|
|
|
|
A |
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
i |
|
|
|||
i |
1, 2, |
3 |
и |
p* |
0 ; |
|
|
p |
* |
|
0,05 * 5 |
0,25 ; |
p* |
0,15*5 |
0,75 . |
Тогда |
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
* |
(0; |
0,25; |
0,75) и предприятие должно произвести 25 % продукции вида А2 , |
|
|
||||||||||||||||||||||
S A |
|
|
|||||||||||||||||||||||||
75 % - вида А3 , а продукцию А1 |
не выпускать. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Оптимальную стратегию |
S * (q , q |
2 |
, q ) находим, |
используя формулу: |
q* |
y |
j |
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
B |
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
j |
|
|
|||
j |
1,2,3 |
и |
* |
0,1* 5 |
0,5 ; |
|
* |
|
0 ; |
|
|
* |
0,1*5 0,5 . Тогда |
* |
(0,5; |
0; |
0,5) |
и |
|||||||||
q1 |
|
q2 |
|
|
q3 |
SB |
|||||||||||||||||||||
оптимальный спрос в 50 % находится в состоянии В1 |
и 50 % в состоянии В4 (с учетом |
||||||||||||||||||||||||||
отброшенной стратегии В2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. Динамическое программирование
Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Модели динамического программирования применяются при разработке правил управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывших из эксплуатации основных фондов
ит.п.
2.1.Задача об оптимальном распределении ресурсов между отраслями
Пример 1. Планируется деятельность двух отраслей производства на 4 года. Начальные ресурсы s0 = 10 000 у.е. Средства х, вложенные в отрасль А в начале года, дают в конце года прибыль f1(x) = 0,6х и возвращаются в размере q1(x) = 0,7х; аналогично для отрасли В функция прибыли равна f2(x) = 0,5х, а функция возврата – q2(x) = 0,8х. В конце года все возвращенные средства заново перераспределяются между отраслями А и В, новые средства не поступают, прибыль в производство не вкладывается.
Требуется распределить имеющиеся средства s0 между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за n лет была максимальной.
Решение. Пусть s0 = 10 000, n = 4, f1(x) = 0,7х, q1(x) = 0,8х, f2(x) = 0,6х, q2(x) = 0,9х.
Введем обозначения. Количество средств, подлежащие распределению на к-ом году - sk-1 (k=1, 2,…, n). Переменных управления на каждом шаге две: хк – количество средств, выделенных отрасли А, и ук – отрасли В. Но так как все средства sk-1

8
распределяются, то ук = sk-1 – хк, и поэтому управление на к-ом шаге зависит от одной переменной хn, т.е. Хк(хк, sk-1 – хк).
Уравнения состояний |
|
Sk=q1(xk)+ q2(sk-1 – хк ) |
(2.1.1) |
выражают остаток средств, возвращенных в конце к-го года.
Показатель эффективности к-го шага – прибыль, полученная в конце к-го года от обеих отраслей:
f1(xк)+ f2(sk-1 – хк). (2.1.2)
Суммарный показатель эффективности – целевая функция задачи – прибыль за n
лет:
n
Z |
f1(xk ) f2 (sk 1 xk ) . |
(2.1.3) |
k 1
Пусть Z k (sk 1) – условная оптимальная прибыль за n-k+1 лет, начиная с к-го года
до n-го года включительно, при условии, что имеющиеся на начало к-го года средства sk-1 в дальнейшем распределялись оптимально. Тогда оптимальная прибыль за n лет
|
|
|
|
|
|
|
|
|
|
|
|
Z |
max |
Z |
* |
(s |
0 |
). |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
Уравнения Беллмана имеют вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Z |
* |
(s |
n 1 |
) |
max |
f |
(x |
n |
) |
f |
2 |
(s |
n 1 |
|
x |
n |
) , |
|
|
|
|
|||||
|
n |
|
0 |
xk |
sk |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z |
* |
(s |
k 1 |
) |
max |
f |
(x |
k |
) |
f |
2 |
(s |
k 1 |
|
x |
k |
) Z |
* |
(s |
k |
) , |
|||||
|
k |
|
0 |
xk |
sk |
1 |
|
|
|
|
|
|
|
|
|
k 1 |
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(k n 1, n 2,...,2) .
(2.1.4)
(2.1.5)
|
|
Используя (2.1.1), запишем уравнение состояний к-го шага: |
|
||||||||||||
|
|
sk =0,8xk+0,9(sk-1– хк), или sk =0,9sk-1 – 0,1хк.. |
(2.1.6) |
||||||||||||
|
|
Целевая функция к-го шага примет вид: |
|
||||||||||||
|
|
0,7хк+0,6(sk-1 – хк)=0,1хк+0,6sk-1. |
|
|
|
|
|
(2.1.7) |
|||||||
|
|
Целевая функция задачи: |
|
|
|
|
|
|
|
||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z = |
0,6sk-1+ 0,1хк.. |
|
|
|
|
|
|
|
|
(2.1.8) |
|||
|
|
к |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим функциональные уравнения, используя (2.1.5): |
|
||||||||||||
|
|
Z * (s |
k 1 |
) |
max |
0,1x |
k |
0,6s |
k 1 |
Z * |
1 |
(s |
k |
) . |
(2.1.9) |
|
|
k |
0 |
xk sk 1 |
|
k |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Проводим условную оптимизацию. |
|
|
|
|
|
||||||||
|
|
4 шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целевая функция имеет вид: |
|
|
|
|
|
|
|||||||
|
|
Z4*(s3 ) |
|
max |
0,6s3 |
0,1x4 . |
|
|
|
|
|
|
|||
|
|
|
|
0 |
x4 |
s3 |
|
|
|
|
|
|
|
|
|
|
|
Т.к. |
х4>0, |
функция – |
Z4*(s3 ) достигает максимума при x*4 (s3 ) |
s3 и равна |
|||||||||
Z |
* |
(s ) |
0,7s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 шаг.
Используя формулу (2.1.9), запишем целевую функцию:
Z3*(s2 ) |
max |
0,1x3 0,6s2 Z 4*(s3 ) . |
0 |
x3 |
s2 |

9
Найдем s3 из уравнений состояний (2.1.6): s3=0,9s2 – 0,1x3 и, подставив его выражение в правую часть уравнения, получим:
|
|
Z3*(s2 ) |
|
max |
|
|
0,1x3 |
|
0,6s2 |
|
0,7 * (0,9s2 0,1x3 ) , |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
x3 |
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z3*(s2 ) |
|
max |
|
|
0,03x3 |
1,23s2 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
x3 |
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.к. x3 > 0, функция Z * |
(s |
2 |
) достигает максимума при x*(s |
2 |
) |
s |
2 |
|
и равна: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|||
|
|
Z3*(s2 ) |
1,26s2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Уравнение состояний при к = 2 имеет вид: s2 = 0,9s1 – 0,1x2. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Целевая функция Z 2*(s1) |
|
|
max |
|
0,1x2 |
0,6s1 |
1,26s2 ) |
|
или |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x2 |
|
s1 |
|
|
|
|
|
|
|
|
|
|
|
Z2* (s1) |
|
max |
|
|
0,026x2 |
1,734s1 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 |
x2 |
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Т.к. x2 |
< |
0, |
функция Z *(s ) |
достигает |
максимума при |
x* |
(s ) |
0 и равна: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
2 |
|
1 |
|
|
Z |
* |
(s ) |
1,734s . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Уравнение состояний при к = 1 имеет вид: s1 = 0,9s0 – 0,1x2. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Целевая функция Z1*(s0 ) |
|
|
max |
0,1x1 |
0,6s0 |
1,734s1) |
|
или |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x1 s0 |
|
|
|
|
|
|
|
|
|
|||
|
|
Z1*(s0 ) |
|
max |
|
|
0,0734x1 |
2,1606s0 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0 x1 s0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Т.к. x1 < 0, функция Z * |
(s |
0 |
) достигает максимума при x*(s |
0 |
) |
0 и равна: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
Z * |
(s |
0 |
) |
2,1606s |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Используя результат оптимизации, получим прибыль от вложения в отрасли А и В |
||||||||||||||||||||||||
за n лет: Zmax |
Z1* (1000) , Zmax |
2,1606 1000 |
2 160,б у.е. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
Итак, в первом году все средства вкладываются в отрасль В ( x* (s |
0 |
) |
0 ), и прибыль |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
от этого составит 600 у.е. (1 000 0,6). В конце года возвращенные средства в размере 900 (1 000 0,9) поступают опять в отрасль В. За второй год прибыль равна 540 (900 0,6). Затем неизрасходованные средства в размере 810 у.е. перераспределяются в отрасль А и приносят прибыль в 567 у.е. (810 0,7). За четвертый год средства, вложенные в отрасль А дают прибыль в 453,6 у.е.(648 0,7). Остаток средств составит
518,4. у.е.
2.2. Замена оборудования
Замена оборудования – это одна из важных проблем любой сферы производственной деятельности. Оборудование изнашивается как физически, так и морально, что ведет к росту производственных затрат, затрат на ремонт и обслуживание, снижению производительности труда.
Поэтому на определенном этапе выгоднее становится приобретение нового оборудования и его эксплуатация, нежели использование старого.

10
Критерием оптимальности являются оптимизация прибыли от эксплуатации оборудования или минимизация затрат на эксплуатацию в течение некоторого периода времени.
Процесс замены оборудования рассматривают как n шаговый, разбивая при этом весь период эксплуатации оборудования на n шагов. На каждом шаге рассматривается вопрос либо сохранить и дальше эксплуатировать оборудование (Хс), либо заменить его на новое (Хз), либо сделать ремонт существующего (Хp).
Пример 2. Оборудование эксплуатируется в течение 5 лет, после этого продается. В начале каждого года можно принять решение, сохранить оборудование или заменить его новым. Стоимость нового оборудования Р0 = 4 000 у.е. После t лет эксплуатации
(1 t 5 ) оборудование можно продать по ликвидной стоимости |
g (t) . Затраты на |
содержание оборудования в течение года определяются функцией |
(t) . Определить |
оптимальную политику замены оборудования, чтобы суммарные затраты были минимальны. В табл. 2.2.1 приведены ликвидная стоимость и затраты на содержание оборудования:
Таблица 2.2.1
t |
0 |
1 |
2 |
3 |
4 |
5 |
(t) |
500 |
600 |
800 |
1 000 |
1 500 |
- |
|
|
|
|
|
|
|
g (t) |
- |
3 000 |
2 500 |
2 000 |
1 200 |
1 000 |
|
|
|
|
|
|
|
Решение. Весь процесс разбивается на 5 шагов.
Показатель эффективности к-го шага определяется формулой
(t), |
если Х к Х э |
|
(2.2.1) |
|
Ft,k min |
|
если Х к |
Х з |
|
t P0 |
(t) g(t), |
, |
||
(t) - затраты на эксплуатацию |
машины |
возраста t. |
При |
замене оборудования |
машина продается по ликвидной стоимости g(t), покупается новая (Р0 = 4 000) и
эксплуатируется в течение первого года |
(t 1) 500 и общие затраты равны 4 500 – |
||
– g(t). Введем новую переменную r(t) = 4 500 – g(t), получим |
|||
(t), |
если |
Х к |
Х э |
Ft,k min |
|
Х к |
(2.2.2) |
t r(t), |
если |
Х з . |
|
Если представить все множество состояний в системе координат, то оценка состояния t,k, т.е. затрат на оборудование возраста t на к–ом году с использованием функционального уравнения Беллмана, представляется следующим образом
(t) |
F |
1,k |
1 |
, |
если |
Х к |
Х э |
Ft,k min |
t |
|
|
|
(2.2.3) |
||
|
|
|
|
|
|
||
t r(t) |
Ft |
1,k |
1, |
если |
Х к |
Х з . |
|
Таким образом в начале интервала планирования оборудование возраста t может: 1) либо эксплуатироваться дальше, и тогда к концу интервала, т.е. к+1, возраст его
станет t+1, а затраты на эксплуатацию определятся как (t 1) . А так как мы
планируем шаг t+1 c конца, то при этом вариант эксплуатации будет учитывать и функции затрат на последующих шагах, т.е. Ft+1, k+1;
2) либо быть проданным по ликвидной стоимости и заменено новым оборудованием, которое будут эксплуатировать на к+1 году с затратами r(t). При этом необходимо учитывать затраты на последующих шагах, т.е. Ft+1, k+1.
Из двух состояний на t+1-ом шаге выбирается то, которое дает наименьшие затраты.
