Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4391

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

580.65 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

При решении этой задачи следует иметь в виду, что в финансовом исчислении Запада расчетный год состоит из 365 дней, если не указано: високосный год или нет.

Пример 1.2. Кредит 130 у.д.е. погашается суммой 150 у.д.е. за 25 дней. Найти простую полугодовую процентную ставку.

Решение: В данной задаче P 130, A 150,t	25	365.	Тогда простая

годовая процентная ставка находится по формуле (1.3):

io	150	130	2,25.

	130	25
		365

Полугодовая процентная ставка

i	1	i0 1,12 .
	2

Пример 1.3. Найти текущую стоимость суммы 250 у.д.е., выплачиваемой через 2 года при простой процентной ставке 10% в год.

Решение: Исходя из формулы (1.2)

P	250		208,33.


1	0,1	2

Наряду с простой процентной ставкой, определяемой формулой (1.3), в финансовом исчислении используется простая дисконтная ставка или учетная ставка, определяемая формулой

d	A P
		.	(1.4)
	At

В терминах учетной ставки текущая и накопленная стоимости связаны

соотношениями

		P		A(1 dt),	(1.5)
A		P

	1		dt .		(1.6)
	1		dt .		(1.6)

Связь между учетной и процентной ставками в единицу времени дается

формулами

i	d	,	(1.7)

	d
1

d . (1.8)

1 i

Пример 1.4. Дисконтировать 200 у.д.е. на 4 месяца при простой

учетной ставке 7 % в год.

Решение: Согласно формуле (1.5)

P 200(1 0,07 13 ) 195,33.

Пример 1.5. Вексель с номинальной стоимостью 200 у.д.е. под 12 %

годовых сроком на 70 дней продается банку с учетной ставкой 10 %

годовых через 30 дней после подписания векселя. Найти а) цену продажи;

б) норму прибыли (в год) продавца; в) норму прибыли (в год) банка.

Решение: Найдем фактическую стоимость векселя по формуле (1.1):

A 200(1 0,12 36570 ) 204,6

A 200(1 0,12 36570 ) 204,6.

Чтобы найти цену продажи, необходимо дисконтировать фактическую стоимость A по формуле (1.5):

P 204,6(1 0,140365) 202,36.

Норма прибыли, как известно, находится по формуле

C Co 100(%),

Cot

где Co - начальная сумма; C - накопленная сумма, t - время накопления. Тогда норма прибыли продавца

n		P1	200	100		202,36 200				100 14,34(%).
	200		30	100		200		30		100 14,34(%).


			365					365
Норма прибыли банка
		A P1			100		204,6		202,36		100 10,1(%).
		P	40		100	202,36			40		100 10,1(%).
		P	40			202,36			40
	1		365							365
	1

3.2. Сложные проценты

Сложные проценты отличаются от простых, как известно, тем, что при

простой процентной ставке i в единицу	времени накопление за n
единиц времени находится по формуле
A P(1 i)n .	(2.1.)

Если простые процентные ставки в различные единицы времени различны: i1 , i2 ,..., in то накопление за n единиц времени находится по формуле

A P(1 i1 )(1 i2 )...(1 in ).

(2.2)

Формулы (2.1) и (2.2) описывают круг задач на сложные проценты, то есть одна из величин находится, если заданы остальные. При этом

дисконтирующий множитель V (n) имеет вид:

		V (n)	1	V n ,

			i)n
		(1	i)n
где V	1	- дисконтирующий множитель за 1единицу времени.

	1 i

Пример 2.1.Фактическая простая процентная ставка на настоящее время составляет 12 % в год, но через 2 года она понизится до 5 % в год. Найти накопление вклада 2 000 у.д.е. за 4 года.

Решение: Согласно формуле (2.2)

A	2000(1	0,12)2	(1	0,05)2	2765,95.
Иногда в реальной практике деловой жизни используются так
называемые номинальные процентные ставки в единицу времени						ih (t)
на срок	h от	момента		времени t .Величина ih (t) определяется		так,

что фактическая простая процентная ставка на срок h равна h ih (t) то есть

A P(1 h ih (t)),

(2.3)

где P - начальный капитал; A - накопленный капитал.

Пример 2.2. Номинальная годовая процентная ставка на срок 3 дня равна 10,8 % Найти накопление капитала 1 000 у.д.е.

Решение: По формуле (2.3) находим

A 1000(1 33650,108) 1000,89.

Определим коэффициент накопления. Для t2 t1 под величиной

A(t1 , t2 ) (коэффициент накопления) будем понимать накопленную стоимость единичной суммы за время t2 t1 от момента t 1.

Из определения A(t1,t2 ) и ih (t) следуют формулы

A(t, t h) 1 h 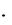ih (t) ,

ih (t)	A(t,t h) 1

	h

Накопление капитала P		находится по формуле
A P A(t1,t2 ).		(2.4)

При нормально функционирующей экономике выполняется принцип согласованности, определяемый при to t1 t2 тождеством

A(t0 , t2 ) A(t0 , t1) A(t1, t2 ).

Пример 2.3. Коэффициент накопления определяется формулой

A(t1,t2 ) exp 0,09(t2 t1)

в единицу времени – 1 год.

Найти:
а) накопление суммы 250 .у.д.е. от момента t				3 на срок h 3
(месяц);
б) проверить принцип согласованности.
Решение: а) по формуле (2.4) находим
A(t0 , t1 )	exp	0,09(t1	t0 ) ,	(2.5)
A(t1,t2 )	exp	0,09(t2	t1) ,	(2.6)
A(t0 , t2 )	exp	0,09(t2	t0 ) .	(2.7)
Перемножая (2.5) и (2.6), получим
A(t0 , t1 )	A(t1, t2 ) exp 0,09(t1 t0 ) 0,09(t2 t1 )
exp 0,09(t2 t0 )			A(t0 , t2 ).

Условие согласованности выполняется.

3.3. Сила процента

Во многих случаях при теоретических исследованиях и практических расчетах используется сила процента, т.е. процентная ставка, изменяющаяся с течением времени по произвольному закону. По определению, сила процента (t) равна пределу номинальной процентной

ставки ih (t) , когда величина h стремится к нулю. Исходя из этого

определения можно получить следующие соотношения между силой процента, коэффициентами накопления и номинальными процентными ставками:

A(t1, t2 ) exp	t2	(t)dt ,
	t1

t h

ih (t) exp t

(t)dt

1 h 1.

Особый интерес представляет случай, когда сила процента постоянна,

т.е.

(t) 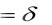const.

В этом случае процентная ставка i в единицу времени связана с 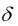формулами

	i	e		1,
		n(1 i).				(3.1)
		n(1 i).
Для номинальной процентной ставки
ih	e	h	1	,

		h
		h
1		n(1		h	i ).
		n(1		h	i ).
	h				n
	h
Для процентной ставки i						в единицу времени
1		i	(1		h ih ) 1h .	(3.2)

, p

целое , тоi

1 i ( p) -

Если

номинальная процентная

ставка,

конвертируемая p раз в единицу

времени. Тогда

( p)

i (1

)

1,i

(1 i)

1 p.

(3.3)

Накопление капитала

при переменной силе процента находится по

формуле

P exp

(t)dt

(3.4)

при постоянной силе процента -

A Pe

(t2 t1 )

P(1

i)t2

t1 .

(3.5)

Пример 3.1. Найти накопленную стоимость 150 у.д.е. за 1,5 года при постоянной силе процента 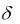0,175 в год. Найти годовую процентную ставку, соответствующую данной силе процента.

Решение: По формуле (3.5)

A 150exp(0,1751,5) 195,03.

По формуле (3.1) i exp(0,175) 1 0,19.

Пример З.2.Накопление происходит при переменной силе процента, определяемой формулой

(t) a bt

в год. Найти a, b , если известно, что сумма 100 у.д.е. дает накопление 125 у.д.е. за 1,3 года, 175 у.д.е. за 2,5 года.

Решение: Согласно формуле (3.4)

		1,3					bt 2		1,3
							bt 2
125	100exp			(a bt)dt 100exp (at				)
125	100exp	0		(a bt)dt 100exp (at			2	)	0
		0							0

100exp(1,3a		1	b 1,32 ),
100exp(1,3a		2	b 1,32 ),
		2
175	100exp(2,5a				1	b 2,52 ).
175	100exp(2,5a			2		b 2,52 ).
				2

Логарифмируя полученные равенства, имеем

n1,25	1,3a 0,845b,
n1,75	2,5a 3,125b.
Решая систему, получим a	0,53; b 0,222 ,
то есть (t) 0,053 0,222t .

Пример 3.3. Процентная ставка в год равна 15 %. Найти эквивалентную ей годовую процентную ставку, конвертируемую ежеквартально.

Решение. Воспользуемся формулой (3.3) при р = 4:

i(4)	(1 0,15) 14 1 4 (1,036 1) 4 0,14.

Пример. 3.4. При i 0,25 найти, эквивалентную процентную ставку, конвертируемую раз в 30 дней.

Решение: Согласно формуле (3.2)

		30			365
1 0,25	(1		i		)	30,

		365	30365
i30365	(1	0,25)	30	365	1	365	0,23.

						30

Если известна сила процента (t) ,то текущая или дисконтированная стоимость P накопленного капитала A находится по формуле

(t )dt

P A e	0	,	(3.6)
	0

дисконтирующий множитель

V (t) e 0

(t)dt

(3.7)

Если сила процента постоянна, то есть (t)					, то
P A e		t	A	,
P A e			(1 i)t	,	(3.8)
					(3.8)
V (t)		1	(1 d )t	e t ,	(3.9)

	(1 i)t

где i - процентная ставка; d - учетная ставка в единицу времени.

Довольно часто в высшем финансовом анализе используется модель силы процента, определяемая формулой Студли:

(t) p	s
		.	(3.10)
	1 re st

Формула (3.10) обладает тем замечательным свойством, что дисконтирующий множитель V (t) равен среднему взвешенному двух дисконтирующих множителей с постоянной силой процента:

V (t)	1		e	( p s)t	r	e	pt .	(3.11)

					1 r
1		r

Пример 3.5. Пусть:

1.Сила процента равна 8 % в год.

2.Сила процента является кусочно-постоянной функцией:

0, 12, 0 t 5,

(t)	0, 08, 5 t 10,

0, 04, t 10

в год.

Найти текущую стоимость суммы 750 у.д.е, накопленной за 20

лет.

Решение.

1. По формуле (3.8)

P	750	e 0,08t	750 e 0,08 20 151,42
2) По формуле (3.6)
		20		5	10	20
P 750 exp		(t)dt	750 exp	0,12dt	0,08dt	0,04dt
		0		0	5	10
750 exp(	5 0,12 0,08 5 0,04 10)			184,95
3.4. Потоки		наличности

Потоки наличности подразделяются на непрерывные и дискретные. Дискретный поток наличности определяется моментами времени

t1 , t2 ,..., tn и вложениями (выплатами или поступлениями)денег

Ct1 , Ct2 ,..., Ctn .

Непрерывные потоки определяются нормой вложений (t) ,где

(t) Ф/ (t) ,

Ф(t) -накопление капитала за время t .
Текущая стоимость на момент времени t		0 для дискретного потока
наличности равна
	n
A(0)	Ct j V (t j ) ,	(4.1)
j	1
для непрерывного -
	t
A(0)	V (t) (t)dt	(4.2)
	0

гдеV (t) дисконтирующий множитель, определяемый формулой (3.7)

Пусть A(t1 ) - текущая стоимость потока наличности на момент времени t t1 . Тогда текущая стоимость данного потока наличности на момент времени t t2 находится по формуле

A(t2 ) A(t1 )	V (t1 )	.	(4.3)
	V (t2 )

Пример 4.1. Пусть

			21
(t)	0,5,	0	t 2,
(t)	0,3,	t	2
	0,3,	t	2

в год. Найти текущую стоимость на момент t 0 непрерывно потока наличности за 5 лет при норме 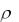1в год начиная с момента времени t 0.

Решение: Найдем вначале дисконтирующий множитель V (t) : а) при 0 t 2

V (t)

exp

(t)dt

exp(

0,5dt)

exp(

0,5 t

t0 )

exp( 0,5t)

б) при t

V (t)

exp(

0,5dt

0,3dt)

exp(

0,5

0,3(t

2))

exp( 0,4

0,3t) .

Итак,

V (t)

0,5t ,

t 2,

e 0,4 0,3t , t

По формуле (4.2)

0,5t

e 0,4

0,3t

A(0)

V (t)dt

0,5 t

0,4

0,3t

0,5

0,3

(e 0,5 2 1)

e 0,4

(e 1,5

e 0,6 )

2(1

e 1)

(e 1 e 1,9 )

1,99.

0,5

0,3

Пример 4.2. Найти цену ежегодной ренты, выплачиваемой в размере 100 у.д.е. в конце каждого года пожизненно с правом наследования, если сила процента равна 7 % в год.

Решение: Данную ренту можно рассматривать как поток наличности, определяемый равенствами

Сt	100, Ct	2	100,..., Ct	n	100,...
1		2		n
где	t1 1,t2		2,...,tn		n,... .

Цена ренты C равна текущей стоимости данного потока наличности на момент времени t 0 . Согласно формуле (4.1)

C A(0)	100e	j
		.	(4.4)
	j 1

Выражение (4.4) есть сумма убывающей геометрической прогрессии, то есть

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2022579.8 Кб04386.pdf
#
13.11.2022579.82 Кб14387.pdf
#
13.11.2022579.85 Кб24388.pdf
#
13.11.2022579.87 Кб24389.pdf
#
13.11.2022580.38 Кб14390.pdf
#
13.11.2022580.65 Кб14391.pdf
#
13.11.2022580.68 Кб14392.pdf
#
13.11.2022580.92 Кб24393.pdf
#
13.11.2022581.01 Кб54394.pdf
#
13.11.2022581.05 Кб44395.pdf
#
13.11.2022581.39 Кб24396.pdf