
3583
.pdf3
Министерство образования Российской Федерации Хабаровская государственная академия экономики и права Кафедра математики и математических методов в экономике
Математическое моделирование
Методические указания и контрольные задания для студентов заочного отделения
Хабаровск 2002
4
ББК В 1 Х 12
Математическая моделирование: Методические указания и контрольные задания для студентов заочного отделения /Сост. Л.А.Дойхен, В.Н.Захарова. – Хабаровск: РИЦ ХГАЭП, 2002. – 24 с.
Методические указания по курсу ''Математическое моделирование'' соотвествуют государственным стандартам; предназначено для студентов заочного отделения. Составлены варианты контрольной работы по курсу.
Рецензент кандидат ф.-м.н., доцент ХГТУ В.Я. Прудников
Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов
Дойхен Людмила Архиповна
Захарова Валентина Никитична
Математическое моделирование Методические указания и контрольные задания для студентов заочного отделения
Редактор Г.С. Одинцова
Подписано в печать 2002г. |
Формат 60 х 84/16 . Бумага писчая. |
|
Печать офсетная. Усл.п.л. 1,4 |
Уч.-изд.л. 1,0 |
Тираж 1300 экз. |
Заказ №
___________________________________________________________
680042, Хабаровск, ул. Тихоокеанская, 134, ХГАЭП, РИЦ.
© Хабаровская государственная академия экономики и права, 2002
5
Предисловие
Данные указания содержат основные вопросы курса, методические указания и контрольные задания для выполнения работ по курсу ''Математическое моделирование''.
В методических указаниях приведены необходимые сведения из отдельных разделов курса. Решены типовые задачи.
Методические указания составлены для студентов-заочников. Перед тем как приступить к решению контрольной работы, необходимо разобрать теоретические вопросы по соответствующему разделу и решения типовых задач.
Основные вопросы курса
1.Система m линейных уравнений с n неизвестными; базисные и свободные неизвестные; понятие базисного решения. Система с базисом. Метод Жордана – Гаусса . Каноническая система. Опорное решение. Метод однократного замещения в канонической системе.
2.Примеры экономико-математических моделей (задачи: использование сырья, о диете, транспортная). Задача линейного программирования (стандартная, основная, общая). Преобразование системы ограничений.
3.Общая теория линейного программирования. Понятие о выпуклых множествах. Множество допустимых решений систем линейных уравнений и неравенств. Экстремум целевой функции.
4.Каноническая задача линейного программирования. Симплексные таблицы. Симплексный метод. Альтернативный оптимум. Графический метод.
5.Двойственность в линейном программировании. Двойственная задача к стандартной и основной. Основная теорема двойственности. Теорема равновесия. Экономическая интерпретация двойственных переменных.
6.Транспортная задача. Разрешимость транспортной задачи. Методы построения исходного допустимого плана. Метод потенциалов.
7.Понятие о нелинейном программировании. Понятие о целочисленном программировании. Простейшие задачи динамического программирования.

6
Методические указания к отдельным темам программы
1. Система с базисом. Метод Жордана – Гаусса
Определение. Система m уравнений с n неизвестными называется системой с базисом, если в ней имеются какие-то m неизвестных, каждое из которых входит только в одно уравнение с коэффициентом единица и не входит в остальные уравнения.
Система с базисом может быть записана, например, так:
x1 + a1, m+1 xm+1 |
+ ... |
+a1n xn |
= a10, |
x2 + a2, m+1 xm+1 |
+ ... |
+a2n xn |
= a20, |
...............................................................
xm + am, m+1 xm+1 + ... +amn xn = am0.
Для того, чтобы произвольную систему m уравнений с n неизвестными привести к системе с базисом, воспользуемся методом Жордана – Гаусса. Рассмотрим систему
a11x1 + a12x2 + ... + a1kxk + ... + a1pxp + ... + a1n xn = a10, a21x1 + a22x2 + ... + a2kx k + ... + a2pxp + ... + a2nxn = a20,
....................................................................................... |
|
|
||||||||||||
ai1x1 + ai2x2 + ... |
+ aikxk |
+ ... |
+ aipxp + ... |
+ ainxn |
= ai0, |
|
|
|||||||
...................................................................................... |
|
|
||||||||||||
as1x1 + as2x2 + + aspxp + + aspxp + + asnxn = as0,... ... ... |
|
|
||||||||||||
...................................................................................... |
|
|
||||||||||||
am1x1 + am2x2 + ... |
+ amkxk + ... |
+ ampxp + ... |
+ amnxn = am0. |
|
|
|||||||||
Составим таблицу Жордана – Гаусса . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
|
|
|
|
xk |
|
|
xp |
|
|
xn |
ai0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 |
|
..... |
|
|
a1k |
|
..... |
a1p |
|
..... |
a1n |
a10 |
|
a21 |
a22 |
|
..... |
|
|
a2k |
|
..... |
a2p |
|
..... |
a2n |
a20 |
|
..... |
..... |
|
..... |
|
..... |
|
..... |
..... |
|
|
..... |
..... |
..... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ai1 |
ai2 |
|
..... |
|
|
aik |
|
..... |
aip |
|
|
..... |
ain |
ai0 |
..... |
..... |
|
..... |
|
|
..... |
|
..... |
..... |
|
|
..... |
..... |
..... |
as1 |
as2 |
|
..... |
|
|
asp |
|
..... |
asp |
|
|
..... |
asn |
as0 |
..... |
..... |
|
..... |
|
|
|
|
|
|
|
|
..... |
..... |
..... |
|
|
..... |
|
..... |
..... |
|
|
|||||||
am1 |
am2 |
|
..... |
|
amk |
|
..... |
amp |
|
..... |
amn |
am0 |
||
1.Выберем разрешающий элемент (asp). Удобно в качестве разрешающего элемента выбирать элемент, равный единице.
2.Элементы разрешающей строки разделим на разрешающий элемент.
3.Элементы остальных строк вычислим по ''правилу прямоугольника'':
Элемент а'ik равен |
aik asp – ask aip |

7
asp
При этом в новой таблице в разрешающем столбце на месте разрешающего элемента asp будет стоять 1, остальные элементы равны нулю. Таких ''единичных столбцов'' надо получить столько, сколько базисных неизвестных имеет данная система.
Приведя систему к системе с базисом и приравняв свободные неизвестные к нулю, мы получим базисное решение системы.
Пример: Найти базисное решение системы.
|
|
|
|
x1 + x2 – x3 + x4 = 2 |
|
||
|
|
|
|
2x1 – x2 +3x3 – 2x4 = 3 |
|
||
|
|
|
|
x1 – x2 + |
x4 =5 |
|
|
Составим таблицу: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
x3 |
x4 |
ai0 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
-1 |
1 |
2 |
|
2 |
|
-1 |
|
3 |
-2 |
3 |
|
1 |
|
-1 |
|
0 |
1 |
5 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
-1 |
1 |
2 |
|
0 |
|
-3 |
|
5 |
-4 |
-1 |
|
0 |
|
-2 |
|
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
-1 |
|
0 |
1 |
5 |
|
0 |
|
7 |
|
0 |
-4 |
-16 |
|
0 |
|
-2 |
|
1 |
0 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
3/7 |
19/7 |
|
0 |
|
1 |
|
0 |
-4/7 |
-16/7 |
|
0 |
|
0 |
|
1 |
-8/7 |
-11/7 |
|
|
|
|
|
|
|
|
Получим систему с базисом |
|
|
x1 + |
3/7x4 = |
19/7 |
x2 - |
4/7x4 = |
-16/7 |
x3 - |
8/7x4 = |
-11/7 |
Здесь x1, x2, x3 – базисные неизвестные, x4 – свободное неизвестное. Положим х4=0. Получим х1= 19/7, х2= -16/7, х3= -11/7. Итак, базисное решение х0=(19/7, -16/7, -11/7, 0). Подставим решение в исходную систему
19/7 - 16/7 + 11/7 = 14/7 = 2,
2 19/7 |
+ 16/7 |
– 33/7 = 21/7 = 3, |
19/7 |
+ 16/7 |
= 35/7 = 5. |

8
Решение найдено верно.
2. Симплексный метод
На предприятии имеется три вида сырья и можно производить два вида продукции. Данные о расходе сырья на производство единицы продукции, запасов сырья и прибыли от реализации единицы продукции предоставлены в таблице
Вид сырья |
Запасы сырья |
Расход сырья на 1 ед. продукции |
|
|
|
А |
В |
1 |
45 |
3 |
4 |
2 |
31 |
5 |
2 |
3 |
30 |
2 |
3 |
Прибыль от реализации 1 ед. |
7 |
5 |
|
продукции |
|
|
|
Найти оптимальный план выпуска продукции, при котором предприятие получит наибольшую прибыль.
Решить задачу симплексным методом и графически.
Решение. Составим математическую модель. Обозначим через х1 и х2 выпуск продукции А и В соответственно. Затраты материала первого сорта на план х (х1, х2) составят 3х1 + 4х2, и они не должны превосходить запасов, т.е. 45 кг:
3х1 + 4х2 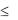 45.
45.
Аналогичны, ограничения по материалу второго сорта
5х1 + 2х2 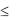 35
35
и по материалу третьего сорта
2х1 + 3х2 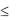 30.
30.
Прибыль от реализации х1 единиц А и х2 – В составит z = 7x1 + 5x2 – целевая функция задачи.
Получили модель задачи: |
|
|
|
3х1 |
+ 4х2 |
45 |
|
5х1 |
+ 2х2 |
35 |
|
2х1 + 3х2 |
30 |
(1) |
|
х1 |
0, x2 |
0 |
|
z = 7x1 + 5x2 |
max |
|
|
Вводом балансовых переменных х3, х4, х5 приводим модель к каноническому виду
3x1 |
+ 4x2 |
+ x3 |
= 45 |
|
5x1 |
+ 2x2 |
+ x4 |
= 31 |
|
2x1 + 3x2 |
|
+ x5 = 30 |
(2) |
|
|
xj 0, (j=1,...,5) |
|
||
z = 7x1 + 5x2 |
max |
|
||

9
Составим симплексную таблицу:
cj |
базис |
аi0 |
7 |
5 |
0 |
0 |
0 |
|
|
(xj) |
|
х1 |
х2 |
х3 |
х4 |
х5 |
|
0 |
x3 |
45 |
3 |
4 |
1 |
0 |
0 |
|
0 |
x4 |
31 |
5 |
2 |
0 |
1 |
0 |
|
0 |
x5 |
30 |
2 |
3 |
0 |
0 |
1 |
|
|
Z |
0 |
-7 |
-5 |
0 |
0 |
0 |
|
Первые три строки этой таблицы содержат в условной форме систему уравнений (ограничений) в задаче (2), а именно: в столбцах ''ai0'' записываются в свободные члены уравнений, в столбцах ''х1'', ''х2'',..., ''х5'' – коэффициенты при соответствующих неизвестных этой системы.
Слева от столбца ''ai0'' в столбце ''xj'' выписываются базисные неизвестные, содержащиеся в соответствующих уравнениях системы.
Верхняя строчка и крайний левый столбец содержат коэффициенты при соответствующих неизвестных в целевой функции z.
Последняя строка называется оценочной, а элементы строки – оценками. Первый элемент а00 оценочной строки представляет собой значение целевой функции z на начальном опорном плане
х0 = (0, 0, 45, 31, 30).
Это значение может быть получено как результат скалярного умножения вектора-столбца ''сj'' на вектор-столбец свободных членов ''аi0''
а00 = 0  45 0
45 0  31 0
31 0  30 0.
30 0.
Оценки при неизвестных вычисляются по правилу: оценка при хj равна сумме произведений элементов первого столбца на соответствующие элементы столбца xj минус коэффициент сj, записанный над столбцом хj. Так оценка при х1 равна
а01 = 0  3 0
3 0  5 0
5 0  2 7
2 7 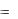 7
7
Оценки при всех базисных неизвестных всегда равны нулю.
Алгоритм симплексного метода
1.Если среди оценок симплексной таблицы при решении на максимум нет отрицательных оценок, то соответствующее опорное решение является оптимальным.
2.Если в оценочной строке содержится отрицательная оценка, над которой в столбце нет положительных элементов, то целевая функция не ограничена сверху на множестве допустимых планов. Задача не имеет решения.

10
3. Если в каждом столбце с отрицательной оценкой есть хотя бы один положительный элемент, то переходим к ''лучшему'' опорному решению. С этой целью:
а) выбираем разрешающий столбец по наименьшей отрицательной оценке;
б) вычисляем ; для этого делим свободные члены на положительные элементы разрешающего столбца. Выделяем разрешающий элемент, соответствующий наименьшиму ;
в) элементы разрешающей строки делим на разрешающий элемент, записываем единичные столбцы соответствующие базисным неизвестным; г)элементы остальных строк вычисляем по ''правилу
прямоугольников''; д) элементы оценочной строки вычисляются также по ''правилу
прямоугольников''. Кроме того, их можно вычислить по правилу нахождения оценок.
Процесс продолжается до тех пор, пока не возникнут ситуации пунктов
1 или 2.
Решим пример, используя алгоритм.
cj |
базис |
аi0 |
7 |
5 |
0 |
0 |
0 |
|
|
(xj) |
|
х1 |
х2 |
х3 |
х4 |
х5 |
|
0 |
x3 |
45 |
3 |
4 |
1 |
0 |
0 |
15 |
0 |
x4 |
31 |
5 |
2 |
0 |
1 |
0 |
31/5 |
0 |
x5 |
30 |
2 |
3 |
0 |
0 |
1 |
15 |
|
z |
0 |
-7 |
-5 |
0 |
0 |
0 |
|
0 |
x3 |
132/5 |
0 |
14/5 |
1 |
-3/5 |
0 |
132/5 |
7 |
x1 |
31/5 |
1 |
2/5 |
0 |
1/5 |
0 |
31/2 |
0 |
x5 |
88/5 |
0 |
11/5 |
0 |
-2/5 |
1 |
88/11 |
|
z |
217/5 |
0 |
-11/5 |
0 |
7/5 |
0 |
|
0 |
x3 |
4 |
0 |
0 |
1 |
-1/11 |
-14/11 |
|
7 |
x1 |
3 |
1 |
0 |
0 |
3/11 |
-2/11 |
|
0 |
x2 |
8 |
0 |
1 |
0 |
-2/11 |
5/11 |
|
|
z |
61 |
0 |
0 |
0 |
1 |
1 |
|
Исходное опорное решение
x1 = (0, 0, 45, 31, 30)
z1 = 0
В оценочной строке две отрицательные оценки: –7, -5. Выбираем в качестве разрешающего столбец, соответствующий х1, т.к. оценка этого столбца (-7) наименьшая отрицательная оценка. Разрешающая строка выбирается по
min 15, |
31 |
,15 |
31 |
, |
|
5 |
5 |
||||
|
|
|
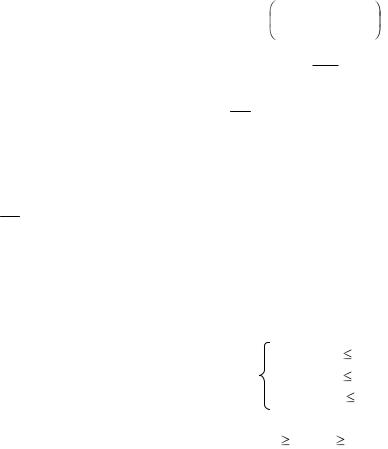
11
этот минимум достигается для 2-ой строки. Итак, в базис вводим х1, выводим из базиса х4. В результате первого шага получаем второе опорное решение
|
|
31 |
|
132 |
|
88 |
|
||
x2 = |
,0, |
,0, |
; |
||||||
5 |
|
5 |
5 |
||||||
|
|
|
|
|
|||||
z2 = 2175 .
После выполнения 2-го шага получаем оптимальное решение:
хопт = (3, 8, 4, 0, 0); zmax = 61
Дальнейшее увеличение z невозможно, т.к. все оценки стали неотрицательными.
Оптимальное решение исходной задачи (1) получается отбрасыванием
из хопт компонент, связанных с балансовыми переменными х3, х4, х5, т.е.
х*опт = (3,8).
При этом значение zmax не изменится.
Теперь дадим геометрическую интерпретацию задачи. Рассмотрим систему неравенств, определяющих множество допустимых планов:
3х1 + 4х2 |
45, |
|
|
||
5х1 + 2х2 |
31, |
|
|
||
2х1 + 3х2 |
30, |
(3) |
|||
х1 0, x2 |
0 |
|
|
||
Построим граничную прямую: |
|
|
|
|
|
3х1 + 4х2 = 45 |
|
|
|
|
|
|
х1 |
|
0 |
45/3 |
|
|
х2 |
|
45/4 |
0 |
|
Прямая 3х1 + 4х2 = 45 плоскостью ХОУ разделила на две части. Чтобы определить полуплоскость, точки которой удовлетворяют неравенству 3х1 + 4х2 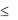 45, следует ''испытать'' одну точку. Проще подставить 0 (0,0).
45, следует ''испытать'' одну точку. Проще подставить 0 (0,0).
Получим верное неравенство: 0<45. Следовательно, полуплоскость включает точку 0 (0,0). Этот факт отмечается стрелочками.
Определяем положение полуплоскостей, отвечающих каждому неравенству и находим пересечение этих полуплоскостей. Два последних условия в (3) означают, что допустимые планы принадлежат неотрицательному квадрату. Тем самым областью решения системы (3) является четырехугольник ОАВС.

12
Линии уровня целевой функции z задаются уравнениями
7х1 + 5х2 = const
Легко видеть, что они образуют семейство параллельных прямых. Вектор N = (7, 5) называется целевым, он перпендикулярен линиям уровня. Этот вектор указывает направление, двигаясь в котором, мы переходим от меньших значений z к большим, т.е. он указывает направление возрастания функции z. Вершина многоугольника, через которую проходит последняя линия уровня, даст наибольшее значение целевой функции. На рисунке видно, что максимальное значение будет достигнуто в вершине В. Найдем координаты точки В. Эта точка лежит на пересечении прямых
5х1 + 2х2 = 31, 2х1 + 3х2 = 30
Решая систему из двух уравнений с двумя неизвестными, находим, что точка В имеет координаты х1 = 3, х2 = 8. Подставляя в целевую функцию найденные значения, получим: zmax 7  3 5
3 5  8 61
8 61
3. Двойственность в линейном программировании
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, называемую двойственной.
Рассмотрим стандартную задачу |
|
|
|
|
z = c1x1 + c2x2 + ..... + cnxn |
max |
|
||
|
|
|
|
|
a11x1 |
+ a12x2 |
+ ..... + a1nxn |
b1, |
y1 |
a21x1 |
+ a22x2 |
+ ..... + a2nxn |
b2, |
y2 |
|
|
|
|
|
