
5665
.pdf
Решение. При решении примера 3 указано, как по эмпирической функции нахо-
дятся варианты xi |
и их относительные частоты |
wi . Из вида данной эмпирической |
||||
функции |
имеем: |
x1 5, x2 10, x3 15 и |
w1 |
0,2 0 0,2 ; w2 0,7 |
0,2 |
0,5 ; |
w3 1 0,7 |
0,3 . Уже имеем один из ответов. |
Так как задан объём выборки |
n |
100 , |
||
то по (3.1) |
получаем следующие значения частот: n1 20, n2 50, n3 30 . |
|||||
Ответ: |
|
|
|
|
|
|
|
|
xi |
5 |
10 |
15 |
|
|
|
ni |
20 |
50 |
30 |
|
|
|
wi |
0,2 |
0,5 |
0,3 |
|
Пример 6. Эмпирическая функция распределения по тарифным разрядам 100 рабочих цеха имеет вид:
|
|
0 |
при |
|
x |
1, |
|
|
|
0,05 |
при |
1 |
x |
2, |
|
F100 |
x |
0,20 |
при |
2 |
x |
3, |
|
0,40 |
при |
3 |
x |
4, |
|||
|
|
||||||
|
|
0,65 |
при |
4 |
x |
5, |
|
|
|
1 |
при |
|
x |
5. |
Найти количество рабочих цеха, имеющих тарифный разряд не ниже четвёртого. Решение. Из определения эмпирической функции (см. (3.2)) и данных примера по
аналогии с решением примера 5 получаем следующий статистический ряд тарифных разрядов:
xi |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
wi |
0,05 |
0,15 |
0,20 |
0,25 |
0,35 |
|
|
|
|
|
|
Во второй строке записаны относительные частоты. Так как n 100, то соответствующие частоты ni (число рабочих, имеющих соответствующий разряд xi ) таковы:
n1 5, n2 15, n3 20, n4 |
25, n5 35 . Тогда число рабочих, имеющих тарифный разряд |
не ниже четвёртого xi |
4 , равно n4 n5 60 . |
Ответ: 60. |
|
Пример 7. Признак |
X генеральной совокупности является непрерывной случай- |
ной величиной. При извлечении случайной выборки наблюдатель получил следую-
щие значения вариант: 127, 121, 112, 114, 100, 111, 131, 117, 105, 109, 107, 155, 135,
140, 103, 145, 99, 100, 95, 150, 102, 122, 120, 115, 120, 110, 120, 100, 132, 105. Требует-
ся провести первичную обработку статистических данных.
Решение. Так как по условию признак является непрерывной случайной величиной, то сведения нужно оформить в виде интервального статистического ряда. В первой строке таблицы заполняются интервалы 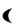
 в возрастающем порядке, во
в возрастающем порядке, во
второй строке – частоты ni вариант, попавших в соответствующий интервал. Полезно найти по формуле (3.1) относительные частоты и заполнить их в следующей строке.
71

Обычно единичные значения вариант, принадлежащие границам интервала, относят к тому промежутку, у которого эта граница является левой (отдельное значение граничной варианты учитывается в правой колонке). В случае чётной частоты можно такое значение распределить поровну в два соседних промежутка, а в случае нечётной – с превышением на единицу в правом промежутке.
Промежутки ai , ai 1 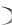 могут быть разной длины, но обычно всё множество выборочных значений разбивают на интервалы равной длины h . Если в таком равномер-
могут быть разной длины, но обычно всё множество выборочных значений разбивают на интервалы равной длины h . Если в таком равномер-
ном вариационном ряду будет r |
частичных интервалов, то для всех i 1, ..., r |
||
|
h |
ai 1 ai . |
(3.6) |
При этом первый интервал |
a1 , a2 |
должен содержать |
xm in , а последний интервал |
ar , ar 1 – xm ax . Не исключено, что эти крайние значения выборки являются кратными. Предварительное значение шага h выборки можно находить по формуле
h |
xm ax xm in |
. |
(3.7) |
|
|||
|
r |
|
|
При необходимости найденное так число h можно округлить до удобного значе-
ния. За начало a1 первого интервала принимается значение |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
a |
x |
|
|
h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.8) |
|||||
|
|
m in |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда концом первого интервала будет число a2 |
a1 |
h (оно же служит началом вто- |
||||||||||||||||||||||||||
рого интервала) и т.д. Отметим, что число xm ax |
xm in |
называется размахом варьирования. |
||||||||||||||||||||||||||
В практической статистике приняты обычные требования: n |
|
30, |
|
r |
5 . |
|
|
|
|
|||||||||||||||||||
Существуют различные рекомендации по выбору числа r |
частичных интервалов |
|||||||||||||||||||||||||||
выборки. Самыми простыми являются приближённые формулы |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
||||||
|
r |
|
n, |
r |
log 2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Второе приближённое равенство из (3.9) называют формулой Стёрджеса. |
|
|
|
|
|
|
||||||||||||||||||||||
В данном примере xm in |
95, xm ax |
|
155 , а n |
30 ; |
xm ax |
|
xm in |
155 |
|
95 |
|
60 |
есть раз- |
|||||||||||||||
мах варьирования. Теперь определимся с числом |
r . |
Так как |
|
n |
|
|
30 |
|
5,477 , а |
|||||||||||||||||||
log 2 n log 2 30 5 log 2 32 |
5 , то, согласно (3.9), |
можно положить r |
6 . Из (3.7) сле- |
|||||||||||||||||||||||||
дует, что такое число групп приведёт к удобному шагу выборки, а именно h |
60 |
10 . |
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
6 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
За начало первого интервала надо взять число |
|
a1 |
95 |
10 |
|
90 |
(см. равенство (3.8). |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Правым концом последнего интервала |
a6 , a7 |
будет |
a7 |
|
a6 |
|
h |
150 . Согласно ска- |
||||||||||||||||||||
занному выше в этот интервал надо отнести единственное значение xm ax |
155 . |
|
|
|||||||||||||||||||||||||
В результате обработки сведений по этой процедуре получим следующий интервальный статистический ряд:
72
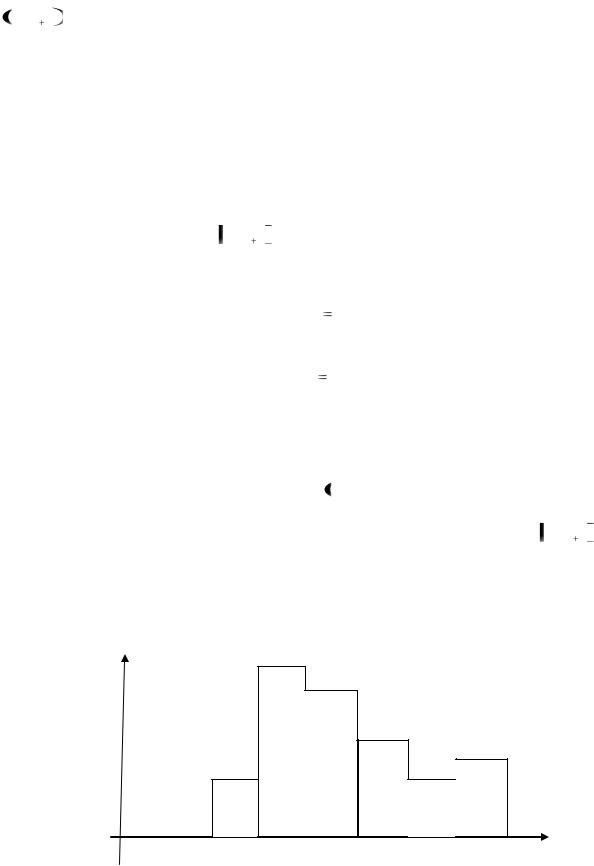
ai , ai 1 |
(90, 100) |
(100,110) |
(110,120) |
(120,130) |
(130,140) |
(140,150) |
|
|
|
|
|
|
|
|
|
ni |
3 |
8 |
7 |
5 |
3 |
4 |
(3.10) |
|
|
|
|
|
|
|
|
wi |
3/30 |
8/30 |
7/30 |
5/30 |
3/30 |
4/30 |
|
|
|
|
|
|
|
|
|
Ответ: сведения обработаны в виде интервального статистического ряда (3.10).
Пример 8. Построить гистограмму относительных частот статистического ряда (3.10). Решение. Геометрическим изображением интервального статистического ряда являет-
ся гистограмма. Различают гистограмму частот и гистограмму относительных частот. Гистограмма – это ступенчатая фигура, состоящая из r прямоугольников, где r
есть число частичных интервалов выборки. Основанием каждого прямоугольника с номером i является отрезок ai , ai 1 . В предположении, что все эти отрезки имеют
одну и ту же длину h , высота hi этого прямоугольника в случае гистограммы частот определяется равенством
h |
|
ni |
, |
(3.11) |
|
|
|
|
|||
i |
|
h |
|
||
|
|
|
|||
а в случае гистограммы относительных частот – равенством |
|
||||
h |
wi |
. |
(3.12) |
||
|
|||||
i |
h |
|
|||
|
|
||||
Нетрудно убедиться, что сумма площадей построенных прямоугольников в случае гистограммы частот равна объёму выборки, а в случае гистограммы относительных частот – единице.
Форма гистограммы относительных частот даёт представление о форме графика плотности (дифференциальной функции) f x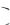 признака X генеральной совокупности как случайной величины.
признака X генеральной совокупности как случайной величины.
При построении гистограммы на оси абсцисс откладывают отрезки ai , ai 1 , а на оси ординат отмечают соответствующие им высоты hi , найденные соответственно по
формулам (3.11), (3.12).
График гистограммы относительных частот изображён на рисунке 21, при этом на оси ординат выбран другой масштаб.
wi / h
8 / 30 |
|
|
|
|
7 / 30 |
|
|
|
|
5 / 30 |
|
|
|
|
4 / 30 |
|
|
|
|
3 / 30 |
|
|
|
|
0 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
x |
Рисунок 21. – Гистограмма относительных частот интервальной выборки (3.10)
Ответ: гистограмма относительных частот построена на рисунке 21.
73

|
Пример 9. Гистограмма частот интервальной выборки объёма n |
100 имеет вид: |
|
||||||||||||||||
|
|
|
|
|
|
ni |
/ h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
4 |
6 |
8 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Рисунок 22. – Гистограмма частот примера 9 |
|
|
|
|||||||||
Требуется найти значение величины a . |
|
|
|
|
|
|
|
||||||||||||
|
Решение. |
Неизвестная величина |
a есть высота |
h4 четвёртого прямоугольника |
|||||||||||||||
a |
h4 |
. Так как высоты hi |
гистограммы частот определяются равенством (3.11), то |
||||||||||||||||
h |
n4 |
. Из рисунка 22 видно, что h |
2 . Тогда h |
n4 и, следовательно, надо найти |
|||||||||||||||
4 |
h |
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
частоту n4 вариант, |
попавших в четвёртый интервал. Поскольку сумма частот равна |
||||||||||||||||||
объёму выборки, |
то |
n4 |
n |
n1 |
n2 |
n3 . Так как объём выборки задан ( n |
100), |
то |
|||||||||||
надо найти частоты n1 , n2 , n3 . Из (3.11) имеем, что ni |
h |
hi . В данном примере h |
2 |
||||||||||||||||
и нужные hi заданы: h1 |
4, h2 |
12, h3 |
18 (см. ось ординат на рисунке 22). Итак, имеем |
|
|||||||||||||||
|
|
|
n1 |
2 h1 |
2 4 8, n2 |
2 h2 |
2 12 24 , n3 |
2 h3 |
2 18 36 . |
|
|
||||||||
Тогда n4 |
100 |
8 |
24 |
36 |
32 |
и, следовательно, |
h4 |
n4 |
32 |
16 . Нужная величина |
|||||||||
h |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
найдена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ответ: a 16 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 10. Случайная выборка некоторого признака |
X генеральной совокупно- |
|||||||||||||||||
сти имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
xi |
5 |
10 |
15 |
20 |
|
|
|
|
|
ni |
10 |
15 |
20 |
5 |
|
|
|
|
|
Найти точечную оценку математического ожидания (генеральной средней) этого признака.
Решение. Известно, что точечной статистической оценкой генеральной средней является выборочная средняя (средняя взвешенная) xв , которая определяется равенством
|
r |
|
|
|
|
xi |
ni |
|
|
xв |
i 1 |
|
, |
(3.13) |
n |
|
|||
|
|
|
|
|
при этом оценка является несмещённой и состоятельной.
74

Так как n 10 15 20 5 |
50 , то из (3.13) получаем |
|
||||
xв |
5 10 |
10 15 |
15 20 |
20 5 |
|
12 . |
|
|
|
|
|
||
|
|
50 |
|
|
||
|
|
|
|
|
|
|
Ответ: точечная оценка математического ожидания равна 12.
Пример 11. Найти точечную несмещённую и состоятельную оценку генеральной дисперсии признака X из примера 10.
Решение. Величину x k , определённую равенством
r
|
|
|
x k n |
i |
|
|
x k |
|
i 1 |
|
|
k 1, 2, 3, ... , |
(3.14) |
|
|
n |
|
|||
|
|
|
|
|
|
|
обычно называют выборочным начальным моментом k -го порядка.
Зная первый и второй выборочные моменты, легко вычислить величину
D |
|
x2 |
x 2 |
, |
(3.15) |
в |
|
|
|
|
|
называемую выборочной дисперсией. |
Отметим, |
что вычисление |
Dв по равенству |
||
(3.15) напоминает вычисление дисперсии дискретной случайной величины по равенству D X  M X 2 M 2 X . Однако выборочная дисперсия является смещённой оценкой для генеральной дисперсии.
M X 2 M 2 X . Однако выборочная дисперсия является смещённой оценкой для генеральной дисперсии.
Несмещённой и состоятельной оценкой генеральной дисперсии является исправленная выборочная дисперсия
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
x 2 . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
s |
2 |
|
|
|
|
D |
|
x2 |
|
(3.16) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
в |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как первый момент x |
(очевидно, что первым выборочным моментом является |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
выборочная средняя) уже вычислена в примере 10, |
то надо вычислить x 2 . Согласно |
||||||||||||||||||||||||||||||
(3.14) и данным выборки, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
52 |
10 |
|
10 2 |
15 |
|
|
15 2 |
20 |
20 2 |
5 |
|
8250 |
|
|
|
|
|
||||||
|
|
|
|
|
|
x 2 |
|
|
165 . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
50 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда по (3.16) получим, что s 2 |
|
50 |
165 |
12 |
2 |
50 |
|
|
21 |
21,43 . |
|
|
|
|
|||||||||||||||||
49 |
|
49 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: D X |
|
|
|
s 2 21,43 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание. Формула (3.16) показывает, |
что |
|
s 2 |
отличается от Dв |
поправочным |
||||||||||||||||||||||||||
множителем |
|
n |
|
|
. Так как lim |
|
n |
1, то при достаточно больших значениях объёма |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
n |
|
1 |
n |
1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выборки s 2 и Dв различаются мало, и поправку можно не делать. При объёме выбор-
ки n 30 в практических приложениях всегда делается поправка, то есть пользуются исправленной выборочной дисперсией.
Пример 12. По результатам интервальной выборки
ai ai 1 |
10-20 |
20-30 |
30-40 |
|
40-50 |
50-60 |
60-70 |
70-80 |
ni |
5 |
10 |
7 |
|
9 |
6 |
5 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|

оценить параметры a, b случайной величины (изучаемого признака X генеральной совокупности), распределённой по равномерному непрерывному закону, и найти её плотность распределения вероятностей.
Решение. Предполагаемое в примере заключение о характере изучаемого признака можно сделать на основе гистограммы данного интервального статистического ряда (рекомендуем построить, например, гистограмму относительных частот). Напомним ещё, что плотность f x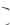 случайной величины X , распределённой по равномерному
случайной величины X , распределённой по равномерному
непрерывному закону, задаётся равенством (2.22). При этом M X и D X выражаются через параметры a, b закона равенством (2.23), то есть
M X |
a b |
, D X |
|
b a 2 |
. |
|
|
2 |
12 |
|
|
||||
|
|
|
|
|
|||
Для нахождения параметров |
a, b применим метод моментов. |
Так как точечной |
|||||
оценкой математического ожидания является выборочная средняя |
M X |
xв , а то- |
|||||
чечной оценкой дисперсии |
является |
исправленная выборочная |
дисперсия |
||||
|
|
n |
|
|
|
|
2 , то |
|
|
|
|
|
|
|
|
||
D X s 2 |
|
|
|
x 2 |
xв |
a, b |
найдутся из системы уравнений: |
||||||||||
|
|
|
|
||||||||||||||
n |
|
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
xв , |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
a 2 |
|
n |
|
|
2 . |
|||
|
|
|
|
|
|
|
|
|
x 2 x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
12 |
|
|
n 1 |
|
|
в |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Этим описана сущность метода моментов: параметры a, b закона находятся с по-
мощью моментов x и x 2 .
Применив для вычисления моментов формулу (3.14), получим для данной выборки систему
|
a |
b |
44,6, |
|
|
|
|
||
|
|
2 |
||
|
|
2 |
|
|
b |
a |
387,6. |
||
|
|
|
|
|
12 |
|
|||
|
|
|||
Или b a |
89,2 , а b a |
68,2 . Тогда a |
10,5 и b |
78,7 . При вычислении моментов за |
||||||||
значения xi |
берутся середины интервалов. |
|
|
|
||||||||
Согласно (2.22), плотность имеет вид: |
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
при |
x |
10,5, |
||
|
|
f |
x |
|
1 |
|
|
при |
10,5 |
x |
78,7, |
|
|
|
|
|
|
|
|||||||
|
|
|
68,2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
при |
x |
78,7. |
||
|
|
|
|
|
0 |
|
|
при |
x |
10,5, |
||
Ответы: a 10,5 ; b |
78,7 |
; |
f x |
1 |
|
|
при 10,5 |
x 78,7, |
||||
|
|
|
|
|
||||||||
68,2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
при |
x |
78,7. |
||
|
|
|
|
|
|
|
|
|
|
76 |
|
|

Пример 13. По результатам интервальной выборки
|
ai ai 1 |
5-10 |
10-15 |
15-20 |
20-25 |
25-30 |
30-35 |
35-40 |
|
|
|
ni |
4 |
7 |
9 |
12 |
|
10 |
8 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
оценить параметры a, |
2 случайной величины |
X , |
распределённой по нормальному |
|||||||
закону, и найти её дифференциальную функцию |
f x . |
|
|
|
||||||
Решение. Дифференциальная функция нормального закона имеет вид (2.28). При этом, согласно (2.29), параметр a совпадает с математическим ожиданием случайной
величины a M X , а параметр |
|
2 – |
с дисперсией 2 D X . Тогда по методу |
|||||
моментов эти параметры находятся из равенств |
|
|||||||
|
|
|
|
n |
|
|
2 . |
|
a x |
, |
2 |
|
x2 x |
||||
|
|
|
||||||
|
|
|
|
|||||
в |
|
|
|
n 1 |
|
|
в |
|
|
|
|
|
|
|
|
||
Последние равенства получаются рассуждениями, аналогичными проведённым
при решении предыдущего примера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По формуле (3.14) получим следующие значения моментов: |
x |
в |
23,05, x2 603,52 . |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда a |
23,05 , а |
2 |
43,30 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Согласно (2.28), дифференциальная функция (плотность) имеет вид: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x 23,05 2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
|
|
e 147,24 . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
43,30 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x 23,05 2 |
|
|
|
|
|
|
|
|
|
|||
Ответы: a 23,05 ; |
|
2 |
43,30 ; |
f x |
|
|
|
|
|
e |
147,24 . |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
43,30 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 14. Оценить параметр |
|
и выписать плотность f |
x |
случайной величины |
|||||||||||||||||||||||||||||||
X , распределённой по показательному закону, по результатам случайной выборки: |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ai |
ai |
1 |
|
0-8 |
|
|
8-16 |
|
16-24 |
|
|
|
24-32 |
|
|
|
32-40 |
|
|
40-48 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ni |
|
|
13 |
|
|
|
11 |
|
9 |
|
|
|
|
7 |
|
|
|
|
|
6 |
|
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. |
Плотность |
|
f |
x показательно (экспоненциально) |
распределённой слу- |
||||||||||||||||||||||||||||||
чайной величины |
X имеет вид (2.24), а параметр |
|
|
закона связан с математическим |
|||||||||||||||||||||||||||||||
ожиданием случайной величины равенством (2.25), |
то есть |
M X |
|
1 |
. Так как не- |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
смещённой и состоятельной оценкой математического ожидания является выбороч-
ная средняя M X xв , то найдётся из равенства |
1 |
xв . Следовательно, |
|
||
|
|
||||
|
1 |
. |
|
(3.17) |
|
|
|
||||
|
xв |
|
|
||
Теперь по данным выборки вычисляем xв по формуле (3.13). За значения xi |
берутся |
||||
середины интервалов данного интервального статистического ряда. В результате получим
77

|
4 13 |
12 11 |
20 9 |
28 7 |
36 6 |
44 |
4 |
|
952 |
19,04 . |
|||
|
xв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
50 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Согласно (3.17), находим |
0,053 . Из (2.24) следует, что f x имеет вид: |
||||||||||||
|
|
f x |
|
|
0 |
|
при |
x |
0, |
|
|
|
|
|
|
|
0,053e 0,053x |
при |
x |
0. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
Ответы: |
0,053 ; |
f |
x |
|
0 |
|
при |
x |
0, |
|
|
||
0,053e |
0,053x |
при |
x |
0. |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
Пример 15. Пусть |
g |
– несмещённая оценка g |
с конечной положительной дис- |
||||||||||
персией D g |
. Будет ли статистика |
|
g 2 несмещённой оценкой для параметра g 2 ? |
||||||||||
Решение. Напомним, что несмещённой называют оценку параметра, математическое ожидание которой совпадает с оцениваемым параметром. Поэтому нам необхо-
димо проверить равенство M g |
2 |
g 2 . По условию g является несмещённой оцен- |
|||||||||||||
|
|||||||||||||||
кой |
параметра |
g , |
откуда |
M g |
g . |
D g |
M g |
2 |
M g |
2 |
и |
потому |
|||
|
|
||||||||||||||
M g |
2 |
g 2 |
D g . Ввиду того, что D g |
0 , то оценка будет смещённой. |
|
||||||||||
|
|
||||||||||||||
Ответ: статистика |
g 2 будет смещённой оценкой для параметра g 2 . |
|
|
||||||||||||
Пример 16. В случае равномерного распределения случайной величины |
X на от- |
||||||||||||||
резке |
|
1 , 1 |
2 |
найти методом моментов точечные оценки параметров |
1 и |
2 . |
|||||||||
Решение. Идея метода моментов состоит в нахождении неизвестных параметров в условиях равенства соответствующих теоретических и выборочных моментов. Напомним, что теоретическим начальным моментом k-го порядка называют величину
|
k |
M X k |
|
; в частности, |
|
|
1 |
M X . Теоретическим центральным моментом k-го по- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рядка |
называют |
величину |
|
k |
|
M X |
M X k , при этом |
2 |
D X . Для |
решения |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
большинства практических задач необходимы только эти два момента ( |
|
1 |
M X |
и |
|||||||||||||||||
|
2 D X ). |
Выборочные |
|
моменты, |
соответствующие им, |
будут a1 |
1 |
n |
и |
||||||||||||
|
|
|
|
xi x |
|||||||||||||||||
|
|
n i |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
1 |
n |
|
|
2 |
, где x , x |
|
|
|
|
|
– выборка объёма n . Систему уравнений для нахож- |
||||||||
b |
2 |
|
x |
i |
x |
|
2 |
, ..., x |
n |
||||||||||||
|
|
||||||||||||||||||||
|
n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дения неизвестных параметров |
|
1 и |
2 |
получим, используя известные выражения для |
|||||||||||||||||
математического ожидания и дисперсии равномерного распределения (см. формулы
(2.23), где a |
1 , b |
1 |
|
2 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
x, |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
x, |
||||
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
, |
или |
|
|
2 |
, |
или |
|
|
. |
|||||||||
|
|
|
|
|
b2 |
b |
a |
|
2 |
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
b2 . |
|
|
|
2 |
|
|
|
b2 . |
||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||||
Из второго уравнения системы выразим |
2 2 |
3b2 ; подставим |
2 в первое, полу- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чим 1 x |
3b2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: 1 |
x |
3b2 , |
2 2 |
|
3b2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
78 |
|
|
|
|
|
|
|
|

Пример 17. Найти методом максимального правдоподобия точечную оценку параметра p геометрического распределения P X m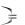 p
p  1 p m 1 , m 1 по выборке
1 p m 1 , m 1 по выборке
x1 , x2 , ..., xn .
Решение. Идея метода максимального правдоподобия состоит в нахождении оценки параметра при условии, что вероятность данного распределения выборки максимальна. Ввиду независимости выборочных значений вероятность выборки (обозначим вероятность выборки через L , которую называют функцией правдоподобия) будет равна произведению вероятностей значений выборки:
|
|
|
n |
|
|
L p 1 p x1 1 p 1 p x2 1 ... |
p 1 p xn 1 |
p n 1 |
p i |
1 |
xi n . |
Перед нами стоит задача нахождения оценки параметра |
p , |
при котором функция L |
|||
достигает максимума. Задачу можно упростить, взяв вместо функции L её натуральный |
|||||
|
n |
|
|
|
|
логарифм, так как функции L и l ln L |
n ln p ( |
xi n) |
ln 1 |
|
p достигают максиму- |
|
i 1 |
|
|
|
|
ма при одном и том же значении параметра p . Необходимым условием максимума (в данном случае оно будет и достаточным) является равенство нулю производной:
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
dl |
|
n i |
|
xi |
n |
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dp |
|
p |
1 |
|
p |
|
|
|
||||
Приводя левую часть равенства к общему знаменателю, получим |
|||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
p n p ( |
xi |
n) или |
|
1 x |
1, или p |
. |
|||||||||||
|
|
p |
|
||||||||||||||||
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
x |
||||
Ответ: p |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 18. Признак X генеральной совокупности подчинён нормальному закону |
|||||||||||||||||||
распределения со стандартом |
X |
1,8 . По случайной выборке объёма n 100 полу- |
|||||||||||||||||
чено значение |
|
xв |
4,6 . Найти доверительный интервал для оценки математического |
||||||||||||||||
ожидания a a M X при надёжности (доверительной вероятности) |
0,95 . |
Решение. При известном стандарте 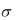 X
X 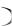 признак X генеральной совокупности с нормальным законом распределения, доверительным интервалом для математического ожидания a является интервал
признак X генеральной совокупности с нормальным законом распределения, доверительным интервалом для математического ожидания a является интервал
xв |
|
|
|
u , xв |
|
|
|
u |
(3.18) |
||||
|
|
|
|
|
|
||||||||
|
|
||||||||||||
|
|
n |
n |
|
|||||||||
с центром в точке xв и радиусом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u , |
|
|
|
(3.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
|||
характеризующим точность (предельную ошибку) интервальной оценки. Число u в
в
(3.19) есть аргумент функции Лапласа (1.16), при котором выполняется равенство
79

|
|
|
|
|
|
|
|
|
u |
|
|
, |
|
|
|
(3.20) |
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
где – заданная надёжность (доверительная вероятность). |
|
|
|
|||||||||||||||
Из |
равенства (3.20) и таблицы |
значений |
функции Лапласа |
найдём |
u : |
|||||||||||||
u |
0,95 |
0,475 ; |
тогда u |
1,96 . |
Теперь по |
формуле (3.19) |
найдём |
: |
||||||||||
|
|
|
||||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1,8 |
|
|
1,96 0,3528 . |
Согласно |
(3.18), |
искомым |
интервалом |
будет интервал |
||||||||||
|
|
|
|
|
||||||||||||||
100 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4,2472 ; 4,9528 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: доверительный интервал 4,2472 ; 4,9528 |
с надёжностью |
0,95 накрывает |
||||||||||||||||
неизвестное математическое ожидание. |
|
|
|
|
|
|
|
|
|
|||||||||
Пример 19. Исследуемый признак |
X |
генеральной совокупности подчинён нор- |
||||||||||||||||
мальному закону распределения, а доверительным интервалом для оценки математи-
ческого ожидания a a M X этого признака является интервал |
20,25; 20,75 . Ука- |
зать точечную оценку математического ожидания a и точность |
данной интерваль- |
ной статистической оценки. |
|
Решение. В случае, когда признак подчинён нормальному закону распределения, симметричные доверительные интервалы для оценки математического ожидания a имеют вид:
xв |
, xв |
, |
(3.21) |
где выборочная средняя xв есть центр этого интервала, а радиус |
является точно- |
||
стью указанной интервальной оценки. Так как интервал (3.21) симметричен относи-
тельно xв , то его длина равна 2 . |
|
|
|
|
|
|
|
|||||||
Пусть доверительным интервалом является интервал c, d . |
Из сказанного выше |
|||||||||||||
следует, что xв |
|
c |
|
d |
и |
d c 2 (тогда |
|
d |
c |
). |
|
|
||
|
|
2 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
По условию примера имеем следующее: |
|
|
|
|
|
|
||||||||
|
xв |
20,25 |
20,75 |
20,5; |
20,72 |
20,25 |
0,25 . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как точечной оценкой для M X является xв , то a 20,5 . |
|
|||||||||||||
Ответы: a 20,5 ; |
0,25. |
|
|
|
|
|
|
|
|
|||||
Пример 20. Точечная оценка математического ожидания a |
нормально распреде- |
|||||||||||||
лённого признака |
X генеральной совокупности равна 10. Выяснить, какой из интер- |
|||||||||||||
валов 1) (10; 10,4); 2) (8,5; 9,5); 3) (9,4; 10,6); 4) (9,6; 10) может быть доверительным интервалом для оценки a .
Решение. По условию дано, что xв 10 . Так как симметричные доверительные ин-
тервалы имеют вид (3.21), то варианты ответов 1) и 4) отпадают (одним из концов этих интервалов является xв 10 ). Отпадает и интервал 2), так как xв 10 ему не при-
80
