
5665
.pdf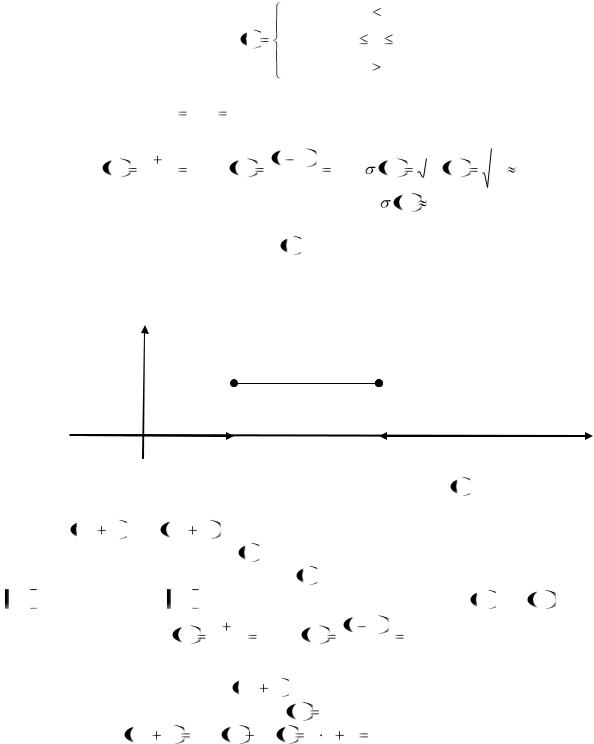
Пример 26. На перекрёстке дорог движение регулируется автоматическим светофором, включающим зелёный свет через каждые 2 минуты. Время простоя у этого светофора автомобиля, остановившегося на красный свет, является случайной величиной, распределённой равномерно на интервале (0, 2) минут. Найти среднее время простоя и среднее квадратическое отклонение.
Решение. Обозначим через X – случайную величину, равную времени задержки автомобиля на перекрёстке. В случае равномерного закона распределения функция плотности имеет вид (см. (2.22)):
|
0 |
при |
x |
0, |
|
f x |
1 |
при 0 |
x |
2, |
|
|
|||||
2 |
|||||
|
|
|
|
||
|
0 |
при |
x |
2. |
Используя (2.23), при a |
0, b |
2 , получим |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 2 |
|
|
|
|
|
|
|
|
|
|
|
0 2 |
|
|
|
2 |
|
1 |
|
|
|
|
|
1 |
0,58 . |
||
M X |
|
1, |
D X |
|
, |
X |
D X |
|||||||||
2 |
|
|
12 |
3 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: 1) среднее время простоя – 1 минута; 2) |
X |
0,58 . |
|
|
|
|
||||||||||
Пример 27. График плотности |
f |
x непрерывной случайной величины X изоб- |
||||||||||||||
ражён на рисунке 14: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y
0,5
0 |
2 |
|
|
4 |
|
|
x |
||
|
Рисунок 14 – График плотности f x |
||||||||
Найти M 4X 2 и D 4X |
2 . |
|
|
|
|
|
|
|
|
Решение. График функции f x |
показывет, что случайная величина распределена по |
||||||||
равномерному закону. Тогда плотность f x |
имеет вид (2.22). В данном примере отрезком |
||||||||
a, b является отрезок 2, 4 . Тогда из равенства (2.23) находим M X и D X : |
|||||||||
M X |
|
2 4 |
|
3, D X |
|
4 2 2 |
|
1 |
. |
2 |
|
12 |
|
6 |
|||||
|
|
|
|
|
|||||
Теперь найдём величину M 4X |
2 . Для этого воспользуемся свойством (2.10) ма- |
||||||||
тематического ожидания и тем, что M C |
C . В результате получим |
||||||||
M 4X 2 4M X M 2 4 3 2 14 . |
|
|
|||||||
|
|
|
|
|
61 |
|
|
|
|
Для нахождения величины |
D 4X |
2 |
воспользуемся следующими свойствами |
||||||||||
дисперсии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
D C |
0 , D C X |
C 2 D X |
при постоянной величине C ; |
|||||||||
2) |
D X |
Y |
D X |
D Y |
при независимости X , Y . |
||||||||
Тогда D 4X |
2 |
42 D X |
D 2 |
16 D X |
0 16 |
1 |
|
8 |
. |
||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
6 |
3 |
|||
Ответы: M 4X 2 |
14 ; D 4X 2 |
8 |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
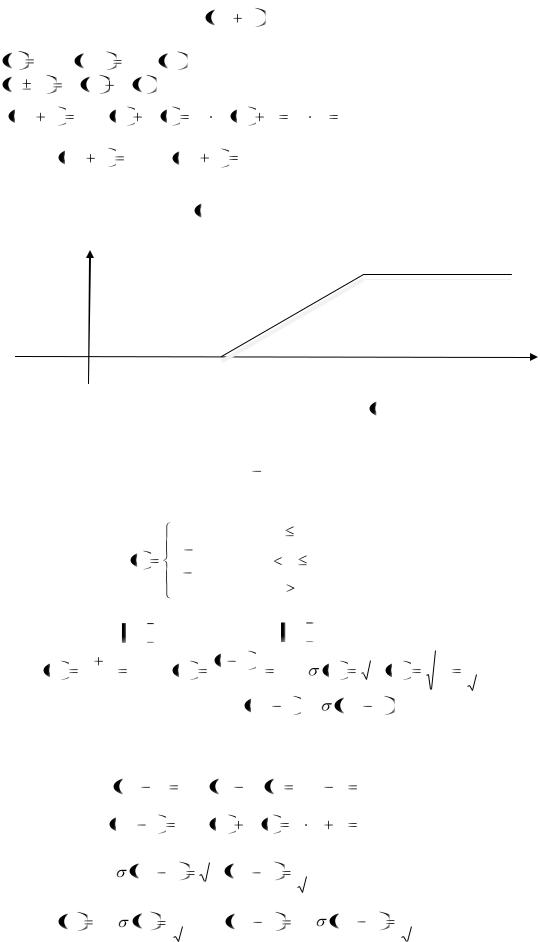
Пример 28. График функции F x распределения случайной величины X имеет вид:
распределения случайной величины X имеет вид:
y
1
0 |
4 |
8 |
x |
Рисунок 15 – График функции F x
Найти математическое ожидание и стандарт случайной величины X , а также те же характеристики случайной величины 2X 4.
Решение. Изображённый график является графиком функции
|
0 |
|
при |
x |
a, |
|
F x |
x |
a |
при |
a |
x b, |
|
|
|
|||||
b |
a |
|||||
|
|
|
|
|||
|
1 |
|
при |
x |
b. |
Это означает, что случайная величина распределена по равномерному закону. В дан-
ном примере отрезком |
a, b служит отрезок |
4, 8 . Тогда из равенств (2.23) имеем, что |
|||||||||||||||
|
|
|
8 4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 8 |
|
|
4 |
|
|
|
|
|
4 |
|
2 |
|
. |
|||
M X |
6, D X |
|
, |
X |
|
D X |
|||||||||||
2 |
12 |
|
3 |
3 |
|
|
|
||||||||||
|
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
Перейдём к нахождению величин M 2X |
4 |
и |
2X 4 . Для этого воспользуемся |
||||||||||||||
перечисленными при решении примера 27 свойствами математического ожидания и дисперсии. Тогда
M 2X 4 2M X
2M X  M 4
M 4 2
2  6 4 8 ,
6 4 8 ,
D 2X 4 2 |
2 D X D 4 4 |
|
4 |
|
0 |
16 |
, |
|
|
|
|
|||||||||||||
|
3 |
|
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
. |
|
|
|
|
|
|
|
|
|||
2 X |
4 |
|
|
|
|
D 2 X |
4 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответы: M X 6 ; X |
|
2 |
|
|
; M 2X |
4 |
8 ; |
|
|
|
|
2 X |
4 |
|
4 |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
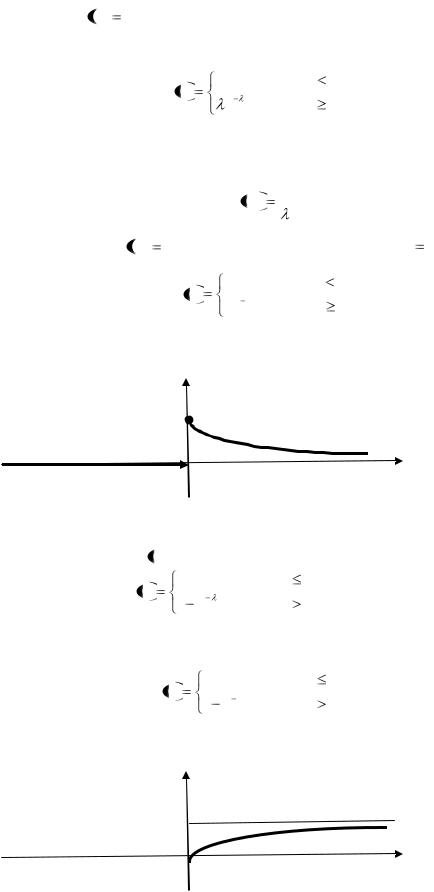
Пример 29. Непрерывная случайная величина распределена по показательному закону, при этом M X 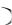 0,25 . Указать дифференциальную и интегральную функции
0,25 . Указать дифференциальную и интегральную функции
этой случайной величины, построить их графики.
Решение. Дифференциальная функция показательного закона имеет вид:
f x |
0 |
|
при |
x |
0, |
(2.24) |
|
e |
x |
при |
x |
0, |
|||
|
|
где 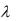 – некоторая положительная постоянная, называемая параметром закона. При этом в случае показательного закона справедливо равенство
– некоторая положительная постоянная, называемая параметром закона. При этом в случае показательного закона справедливо равенство
M X |
1 |
. |
(2.25) |
|
Так как по условию M X  0,25 , то из (2.24) получаем, что
0,25 , то из (2.24) получаем, что 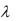 4 . Следовательно,
4 . Следовательно,
f x |
0 |
|
при |
x |
0, |
|
4e |
4 x |
при |
x |
0. |
||
|
График этой функции изображён на рисунке 2.7. y
4
0 |
x |
Рисунок 16 – График дифференциальной функции примера 29
Интегральная функция F x показательного закона с параметром
показательного закона с параметром 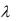 имеет вид:
имеет вид:
F x |
0 |
|
при |
x |
0, |
(2.26) |
|
1 e |
x |
при |
x |
0. |
|||
|
|
||||||
|
|
|
В данном примере этой функцией будет функция
F x |
0 |
|
при |
x |
0, |
|
1 e |
4 x |
при |
x |
0. |
||
|
Её график изображён ниже
y
1
|
x |
0 |
Рисунок 17 – График интегральной функции примера 29
63

|
|
0 |
при |
x |
0, |
|
0 |
|
при |
x |
0, |
|
|
Ответы: 1) |
f x |
4e 4 x |
при |
x |
0. ; 2) F x |
1 |
e |
4 x |
при |
x |
0. |
; |
3) |
графики функций изображены на рисунках 16, 17. |
|
|
|
|
|
|
|
|
|||||
Пример 30. |
Найти вероятность события 0,5 |
X |
|
2,5 , |
если случайная величина |
||||||||
распределена по закону примера 29.
Решение. Если случайная величина распределена по показательному закону с па-
раметром |
, то справедливо равенство |
|
|
|
|
|
|
|
|
|
P a X |
b |
e |
a |
e |
b . |
(2.27) |
В предыдущем примере установлено, |
что |
|
4 . |
По |
условию этого примера |
|||
a 0,5, b |
2,5 . Тогда по (2.27) имеем |
|
|
|
|
|
|
|
|
P 0,5 |
X 2,5 e 4 0,5 |
e 4 2,5 |
e 2 |
e 10 |
0,1353 . |
||
Ответ: P 0,5 X 2,5 |
0,1353 . |
|
|
|
|
|
|
|
Пример 31. Известно, что срок службы изделия распределён показательно со средним 2 года. Найти вероятность того, что изделие прослужит не менее: 1) одного года; 2) трёх лет.
Решение. Обозначим через X – случайную величину, равную сроку службы изделия. По условию она имеет показательное распределение с некоторым параметром . Соглас-
но (2.25) |
M X |
1 |
|
2 , откуда |
|
0,5 . Далее, используя равенство (2.27), получим |
||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
P X |
1 |
P 1 |
X |
e 0,5 |
e |
0,61 , |
|
|
|
|
P X |
3 |
P 3 |
X |
e 1,5 |
0,22 . |
|
Ответы: 1) P X |
1 |
0,61 ; 2) P X 3 |
0,22 . |
|
|
|||||
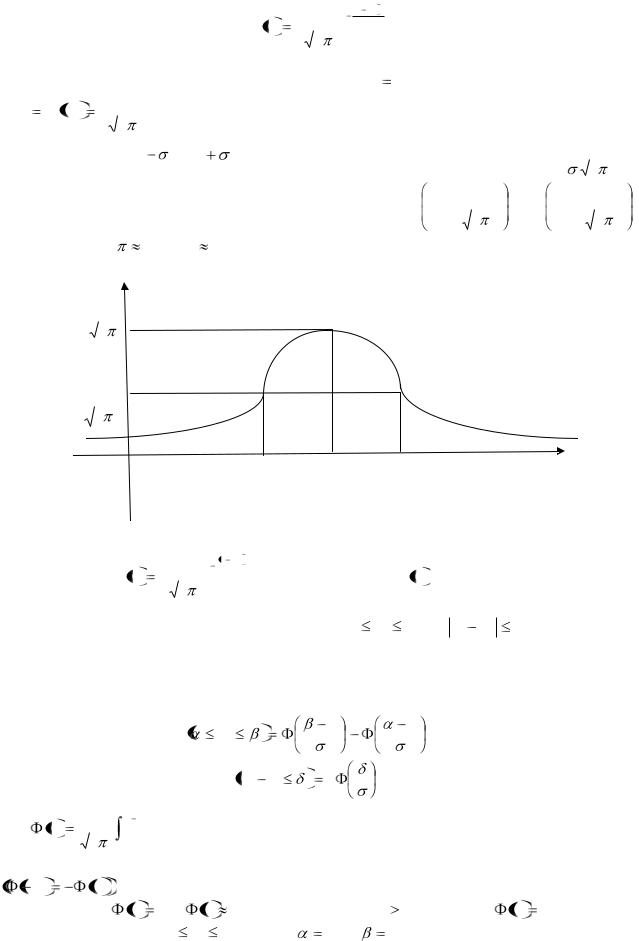
Пример 32. Непрерывная случайная величина распределена по нормальному закону, при этом M X  50,
50,  X
X  5 . Выписать плотность распределения вероятностей случайной величины и построить график этой функции.
5 . Выписать плотность распределения вероятностей случайной величины и построить график этой функции.
Решение. Если случайная величина имеет нормальный закон распределения, то её плотность f x имеет вид
|
|
|
|
1 |
|
|
|
x |
a 2 |
|
|
|
|
f |
x |
|
|
|
e 2 |
2 , |
(2.28) |
||||
|
|
|
|
|
|
|||||||
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
где постоянные a, |
0 есть параметры этого закона. Доказывается, что |
|
||||||||||
|
M X |
a, |
|
|
X |
. |
|
(2.29) |
||||
График функции (2.28) называют нормальной кривой, или кривой Гаусса. В силу условий данного примера получим, что
64
f x |
|
1 |
|
e |
|
|
|
|
|
||
|
|
|
|
||
|
|
||||
5 |
2 |
|
|
||
 x 50 2
x 50 2
50 .
Эта |
функция |
|
|
имеет |
максимум |
в точке |
x |
50 . |
При |
этом |
очевидно, |
|
что |
|||||||||||||||||||||||||||
ym ax f |
50 |
|
|
|
|
1 |
|
|
|
|
. График функции (2.28) имеет две точки перегиба, абсциссы ко- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
5 |
2 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
торых есть точки |
a |
и a |
|
на оси Ox , а ординаты совпадают и равны |
|
1 |
|
. В |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2 e |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
данном |
примере |
точками |
|
перегиба |
являются |
точки |
45, |
|
1 |
|
|
и |
55, |
1 |
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 e |
|
|
|
5 2 |
|
e |
|||||||
Напомним, что |
|
|
|
|
|
3,14, |
|
e |
|
|
2,72 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Примерный график кривой Гаусса этого примера изображён на рисунке 2.7. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
50 |
|
55 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 18 – График кривой Гаусса примера 32 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x 50 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы: 1) |
f |
x |
|
e |
50 |
; 2) график кривой |
f x |
изображён на рисунке 18. |
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 33. Найти вероятности событий 45 X 60 и X 50 5 для случайной
величины примера 32.
Решение. Известно, что для случайной величины, распределённой по нормальному закону, справедливы равенства
|
|
|
|
|
|
|
|
|
P |
X |
a |
|
|
|
a |
, |
(2.30) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(2.31) |
||
|
|
|
|
1 |
|
|
x |
t 2 |
|
P |
X a |
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
|
x |
|
|
|
e |
2 dt есть так называемая функция Лапласа, для вычисления значе- |
|||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
2 |
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ний |
которой |
имеются таблицы. Напомним, |
что эта |
функция |
является нечётной |
|||||||||||||||
|
x |
|
|
x |
|
|
, так что в таблице присутствуют только неотрицательные аргументы. |
|||||||||||||
Очевидно, что 0 0; |
5 |
0,499997 ; для всех X |
5 полагают |
x 0,5 . |
|
В случае события 45 |
X |
60 имеем |
45, |
60 и тогда по |
(2.30) получим |
|
|
|
65 |
|
|
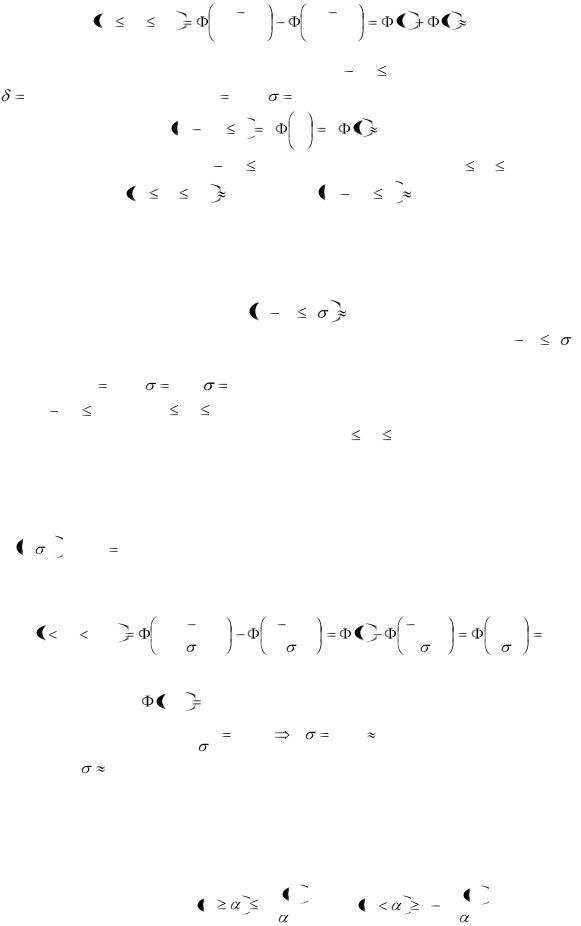
P 45 |
X |
60 |
|
|
60 |
|
50 |
|
|
|
|
45 |
|
50 |
|
|
2 |
1 |
0,8185 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для нахождения вероятности события |
X |
50 |
5 |
применим формулу (2.31) при |
||||||||||||||||||||
5 (по условию примера a |
50, |
|
5 ). Тогда |
|
|
|
||||||||||||||||||
|
|
P |
|
X |
50 |
|
5 |
2 |
5 |
|
2 |
1 |
|
0,6826 . |
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
5 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим, что событие |
|
X |
50 |
|
5 равносильно событию 45 |
X 55. |
||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответы: 1) |
P 45 |
X |
60 |
|
|
0,8185 ; 2) P |
X |
50 |
|
5 |
0,6826. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 34. Выяснить, что означает правило трёх сигм для случайной величины примера 32.
Решение. Для случайной величины, распределённой по нормальному закону, справедливо приближённое равенство
|
|
|
|
P |
X a |
3 |
0,9973, |
|
(2.32) |
|
|
|
|
||||||
называемое правилом трёх сигм. Так как вероятность события |
X a |
3 близка к |
|||||||
единице, то это означает, что данное событие практически достоверно. |
|
||||||||
Так как a |
50, |
5 ( 3 15 ), то в данном случае практически достоверно собы- |
|||||||
|
|
|
|
|
|
|
|||
тие |
X 50 |
|
15 или 35 |
X 65. |
|
|
|
||
Ответ: практически достоверно событие 35 |
X 65. |
|
|||||||
Пример 35. Коробки с шоколадом упаковываются автоматически, и их средняя масса равна 1,05 кг. Найти стандартное отклонение, если 5 % коробок имеет массу менее 1 кг. Предполагается, что масса коробок распределена по нормальному закону.
Решение. Случайная величина X – вес коробки имеет нормальное распределение N a, 2 , где a 1,05 , а стандартное отклонение  неизвестно. Так как 5 % коробок имеет вес менее 1 кг, то, ввиду симметрии относительно математического ожидания, 45 % коробок имеют вес в интервале от 1 кг до 1,05 кг. Поэтому, согласно формуле (2.30), получаем
неизвестно. Так как 5 % коробок имеет вес менее 1 кг, то, ввиду симметрии относительно математического ожидания, 45 % коробок имеют вес в интервале от 1 кг до 1,05 кг. Поэтому, согласно формуле (2.30), получаем
P 1 X 1,05 |
1,05 |
1,05 |
1 |
1,05 |
0 |
0,05 |
0,05 |
0,45 . |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
В данном случае мы использовали свойство нечётности функции Лапласа. В таблице находим, что 1,65 0,45 , поэтому
|
0,05 |
1,65 |
0,05 |
0,03 . |
|
|
|
|
|
||
|
|
|
1,65 |
||
|
|
|
|
|
|
Ответ: |
0,03. |
|
|
|
|
Пример 36. Средний вес клубня картофеля равен 100 г. Оценить вероятность того, что наудачу взятый клубень весит менее 300 г.
Решение. Случайная величина X – вес клубня – неотрицательная, поэтому для оценки веса клубня можно применить неравенство Маркова
P X |
M X |
или P X |
1 |
M X |
. |
(2.33) |
|
|
|||||
|
|
66 |
|
|
|
|
Воспользуемся вторым неравенством (2.33), в данном случае  300, а в качестве математического ожидания M X
300, а в качестве математического ожидания M X  нужно взять средний вес клубня. Тогда
нужно взять средний вес клубня. Тогда
|
|
|
|
|
|
|
|
P X |
300 |
1 |
100 |
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
300 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ответ: P X |
300 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 37. Оценить вероятность события 32 |
X |
72 , если случайная величина |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
имеет следующие характеристики: |
M X |
52, |
|
X |
2 |
|
6 . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Событие 32 |
X |
72 |
равносильно событию |
X |
52 |
|
20 . |
Вероятность |
||||||||||||||||||||||||
этого события можно оценить по неравенству Чебышева |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D X |
. |
|
|
|
(2.34) |
|||||||||||
|
|
|
|
|
|
|
P |
X |
|
M X |
|
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||||||||||||||||||
Положив в (2.34) |
20 (при этом по условию M X |
|
|
|
|
|
|
|
24 ), получим |
|||||||||||||||||||||||
52, |
|
|
|
D X |
X |
|||||||||||||||||||||||||||
|
|
|
|
|
P |
|
X |
52 |
|
20 |
1 |
24 |
|
376 |
|
0,94 . |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
202 |
|
400 |
|
|
|
|
|||||||||||||||||||
Ответ: P 32 |
X |
72 |
|
0,94 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 38. На заводе в среднем 70 % продукции первого сорта. С надёжностью 0,9 найти границы, в которых должна находиться относительная частота первосортной продукции в партии 10 000 единиц.
Решение. Пусть X – относительная частота первосортной продукции в партии
из10 000 единиц. Тогда X |
|
|
n |
. В данном случае |
|
– число первосортных изделий |
|||||||||||||||||||||||||||||||||||||||
|
|
|
n |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
из 10 000.Случайная величина |
|
n |
распределена по закону Бернулли B 10 000; 0,7 |
. Из- |
|||||||||||||||||||||||||||||||||||||||||
вестно (см. (2.12)), что M |
|
|
|
|
|
n p, D |
|
n n |
p |
1 |
p |
и |
D |
n |
|
|
D n |
|
|
p |
1 |
p |
. |
||||||||||||||||||||||
|
n |
|
|
|
|
n |
|
|
n2 |
|
|
|
n |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применяя (2.34), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
n |
|
10000 |
0,7 |
|
|
|
1 |
0,7 |
1 |
|
0,7 |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
10000 |
|
|
|
|
|
10000 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Левая часть неравенства – надёжность, которая по условию примера равна 0,9. Поэтому |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
P |
n |
0,7 |
|
|
|
0,9 |
1 |
0,0001 |
|
|
0,0001 |
0,1 |
|
|
|
|
|
|
0,0001 |
0,032 . |
|
|
|
||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда |
|
n |
0,7 |
|
0,032 |
или 0,7 |
0,032 |
|
|
n |
0,7 |
0,032 . Окончательно получим |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,668 |
|
|
n |
|
0,732 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: 0,668 |
|
n |
|
0,732 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Модуль 3. Математическая статистика
Пример 1. Наблюдатель провёл случайную выборку из генеральной совокупности и зафиксировал в порядке появления значения xi изучаемого признака X генераль-
ной совокупности, которыми оказались следующие числа: 4, 2, 5, 4, 4, 3, 4, 5, 4, 4, 5, 2, 2, 4, 5. Требуется произвести первичную обработку полученных случайных сведений.
Решение. Случайные сведения оформляются в виде таблицы, называемой распределением выборки или дискретным статистическим рядом. В верхней части этой таблицы записываются наблюдаемые значения (варианты) xi изучаемого признака в воз-
растающем порядке от xm in до xm ax , каждое значение записывается только один раз. Такая запись называется вариационным рядом. Во второй строке записываются ча-
стоты ni соответствующих значений |
xi или относительные частоты wi этих же зна- |
||||||||||||||||||||||||||||||||||
чений, которые определяются равенством |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
ni |
, |
|
|
|
|
|
|
|
|
(3.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
где n |
|
|
ni |
есть объём выборки. Часто в таблице заполняется как строка частот ni , |
||||||||||||||||||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
так и строка относительных частот wi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
В данном примере |
xm in |
|
|
2, xm ax |
5 . Тогда вариационный ряд имеет следующий |
|||||||||||||||||||||||||||||
вид: 2, 3, 4, 5. Видно, |
что частоты этих значений таковы: n1 |
3, n2 |
1, n3 |
7, n4 |
4 . |
||||||||||||||||||||||||||||||
Тогда |
|
n |
n1 |
n2 |
n3 |
n4 |
15 есть |
объём |
данной |
выборки. |
По |
(3.1) |
получаем |
||||||||||||||||||||||
w |
3 |
|
, w |
|
|
1 |
, w |
|
7 |
, w |
|
|
4 |
. Отметим, что всегда справедливо очевидное равен- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
15 |
2 |
15 |
3 |
15 |
4 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ство |
|
wi |
1. Итак, распределение выборки имеет вид: |
|
|
|
|
||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
2 |
|
|
|
3 |
|
4 |
|
5 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ni |
|
|
|
|
3 |
|
|
|
1 |
|
7 |
|
4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
wi |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
7 |
|
|
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
15 |
|
15 |
|
15 |
|
|
|
|
|
|
|||||||
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
2 |
|
|
|
3 |
|
4 |
|
5 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ni |
|
|
|
|
3 |
|
|
|
1 |
|
7 |
|
4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
wi |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
7 |
|
|
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
15 |
|
15 |
|
15 |
|
|
|
|
|
|
|||||||
|
Пример 2. Построить полигон дискретного статистического ряда примера 1. |
|
|||||||||||||||||||||||||||||||||
|
Решение. Геометрической характеристикой дискретного статистического ряда |
||||||||||||||||||||||||||||||||||
являются полигоны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Полигоном частот называют ломаную линию, отрезки которой соединяют точки |
||||||||||||||||||||||||||||||||||
xi , ni |
. При построении полигона частот на оси Ox откладывают варианты xi , |
а на |
|||||||||||||||||||||||||||||||||
оси ординат – соответствующие им частоты ni . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Полигоном относительных частот называют ломаную линию, отрезки которой соеди- |
||||||||||||||||||||||||||||||||||
няют точки |
|
xi , wi |
. Для построения такого полигона варианты xi |
снова откладывают на |
|||||||||||||||||||||||||||||||
оси абсцисс, а соответствующие им относительные частоты wi – на оси ординат. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
|
|
|
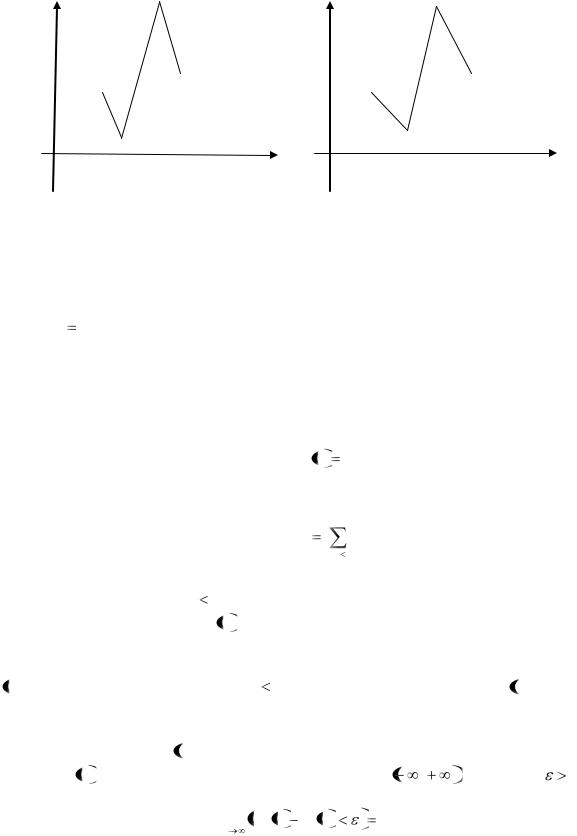
По виду полигонов можно предположить, какому теоретическому закону подчинён изучаемый признак.
Ниже на рисунках изображены полигоны рассмотренного статистического ряда.
|
ni |
|
|
|
wi |
|
7 |
|
|
|
7 /15 |
|
|
4 |
|
|
|
4 /15 |
|
|
3 |
|
|
|
3/15 |
|
|
1 |
|
|
|
1/15 |
|
|
0 |
2 3 |
4 5 |
x |
0 |
2 3 4 5 |
x |
|
Рисунок 19 – График |
|
|
Рисунок 20 – График |
|
|
|
полигона частот |
|
полигона относительных частот |
|
||
При построении полигонов выбраны разные масштабы по осям ординат.
Графики полигонов похожи друг на друга. При соблюдении масштаба график полигона относительных частот будет сжат относительно оси ординат в n раз (в данном примере n 15).
Ответы: 1) на рисунке 19 изображён полигон частот; 2) на рисунке 20 изображён полигон относительных частот.
Пример 3. Найти эмпирическую функцию распределения выборки примера 1. Решение. Эмпирическая функция распределения выборки определяется равенством
F x |
nx |
, |
(3.2) |
|
|||
n |
n |
|
|
|
|
||
где n – объём выборки, а n x – сумма частот вариант, которые меньше x . Число n x можно описать в виде формулы
|
nx |
ni . |
(3.3) |
|
|
i: xi x |
|
В записи (3.3) проводится суммирование частот ni |
по тем индексам i , для которых |
||
выполняется неравенство xi |
x . |
|
|
Интегральную функцию |
F x распределения признака (случайной величины) X |
||
генеральной совокупности будем называть теоретической функцией. Различие между теоретической и эмпирической функциями состоит в том, что теоретическая функция F x задаёт вероятность события X x , а эмпирическая функция Fn x
задаёт вероятность события X x , а эмпирическая функция Fn x даёт относи-
даёт относи-
тельную частоту этого же события.
Очевидно, что эмпирическая функция обладает свойствами теоретической функции. При этом Fn x является хорошей оценкой (хорошим приближением)
является хорошей оценкой (хорошим приближением)
функции F x , так как для любого аргумента x |
из |
, |
и любого |
0 спра- |
||
ведливо равенство |
|
|
|
|
||
|
|
1, |
|
|
(3.4) |
|
lim |
Fn x F x |
|
|
|
||
n |
|
|
|
|
|
|
69 |
|
|
|
|
||

являющееся упрощенным вариантом теоремы Гливенко – Кантелли. Равенство (3.4) практически означает следующее: значения неизвестной теоретической функции F x можно вычислить по значениям эмпирической функции Fn x
можно вычислить по значениям эмпирической функции Fn x сколь угодно точно при
сколь угодно точно при
выборках достаточно большого объёма.
Из ответа примера 1 и равенств (3.2), (3.3) получим, что Fn x имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
при |
|
|
|
x |
2, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
при |
2 |
x |
3, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Fn 15 |
x |
4 |
|
|
при |
3 |
|
x |
4, |
|
|
|
(3.5) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
при |
4 |
x |
5, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
при |
|
|
|
x |
5. |
|
|
|
|
|
|
|||
|
Отметим следующее. Значения x |
|
|
2, x |
3, x |
4, x 5 (правые концы промежутков) |
||||||||||||||||||||||||||
есть варианты ряда. Соответствующие относительные |
частоты получаются так: |
|||||||||||||||||||||||||||||||
w |
3 |
0 |
|
3 |
, w |
4 |
3 |
1 |
|
, w |
11 |
|
4 |
|
7 |
|
, w |
1 |
11 |
|
4 |
, то есть получаются |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
15 |
|
15 |
2 |
15 |
15 |
15 |
3 |
15 |
|
15 |
15 |
4 |
|
15 |
15 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
путём вычитания из значения функции на следующем промежутке её значения на предыдущем промежутке.
Ответ: эмпирическая функция задаётся формулой (3.5).
Пример 4. Найти частоту |
n3 значения x3 |
20 , если дискретный статистический |
||||||||||||
ряд объёма n 50 имеет вид: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
5 |
|
10 |
|
20 |
30 |
|
||||||
|
wi |
|
1 |
|
|
|
2 |
|
|
w3 |
|
1 |
|
|
|
|
5 |
|
|
5 |
|
|
|
10 |
|
|
|||
Решение. Распределение выборки задано так, что указаны относительные частоты
wi значений |
xi . Так как |
wi |
1 (см. пример 1), то w3 1 |
1 |
2 |
1 |
1 0,7 |
0,3 . |
|||
|
|
|
|
|
|||||||
5 |
5 |
10 |
|||||||||
|
|
i |
|
|
|
||||||
По (3.1) имеем равенство n3 |
n w3 . По условию примера n |
50 , а значение w3 |
уже |
||||||||
найдено ( w3 |
0,3 ). Таким образом, n3 50 0,3 15 . |
|
|
|
|
|
|
|
|||
Ответ: n3 |
15 . |
|
|
|
|
|
|
|
|
|
|
Замечание. Решение данного примера поможет выполнить тестовое задание 22 на странице 9.
Пример 5. Найти дискретный статистический ряд, если эмпирическая функция выборки объёма n 100 имеет вид:
|
|
0 |
при |
x |
|
5, |
|
Fn |
x |
0,2 |
при |
5 |
x |
10, |
|
0,7 |
при |
10 |
x |
15, |
|||
|
|
||||||
|
|
1 |
при |
x |
|
15. |
|
|
|
|
|
70 |
|
|
