5665

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

больше 10. Тогда m B

6 и по (1.1) P B

Исходы множества

1,2; 1,5; 2,1; 2,4; 3,3; 3,6; 4,2; 4,5; 5,1; 5,4; 6,3; 6,6 и только они будут

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

2.86 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Задание 24. Если генеральная совокупность имеет нормальное распределение, то вероятность того, что выборочное среднее будет меньше генеральной средней, равна …

Варианты ответов: 1) 0; 2) 1; 3) 0,5; 4) 0,3.

Решение.		Пусть		X ~ N a,	2 ,	тогда	известно, что		xв a	~ N 0, 1 . Поэто-
Решение.		Пусть		X ~ N a,	2 ,	тогда	известно, что			~ N 0, 1 . Поэто-
му P xв a	P		xв a	0 0,5 .
му P xв a	P			0 0,5 .
Задание 25. Неизвестная случайная величина X имеет функцию распределения
					0	при	x	0,
				F x	x	при 0	x	1,
					1	при	x	1.

Тогда оценка параметра , полученная методом моментов, равна …

Варианты ответов: 1)	xв ; 2)		xв	; 3)	xв	; 4)	1	xв	.

		1	xв		1 xв		1	xв

Решение. Для того чтобы найти математическое ожидание случайной величины,

вычислим плотность распределения f x						F	x	:
			0		при			x		0,
	f	x	x	1	при		0		x	1,
	f	x	x		при		0		x	1,
			0		при			x		1.
		1				x	1		1
		1					1		1
Тогда M X	xf x dx	x	x 1dx								. Из равенства теоретического


		0					1		0	1
		0					1		0

момента (математического ожидания) и выборочного момента (выборочного средне-

го) получим оценку параметра		:
	xв	xв	xв		ˆ	xв	.
	xв	xв	xв		ˆ	xв	.
1					1	xв
Задание 26. Неизвестная случайная величина X имеет функцию распределения:
	F x	0	при	x	0,
	F x	1 e x2	при	x	0.

Тогда оценка параметра , полученная методом максимального правдоподобия, имеет вид …

Варианты ответов: 1)

xв ; 2)

; 3)

; 4)

xв

n i

n i 1

Решение. Найдём плотность распределения случайной величины X :

f x

при

Составим функцию правдоподобия L

... f xn

L 2 x e

x12 2

x22

... 2

xn2

e i 1 i .

i 1

Оценку параметра 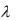найдем из условия максимума логарифма функции правдо-

подобия l ln L n ln 2 n ln

x 2

. Тогда

i 1

x 2

n i 1

Задание 27. Ежедневная заработная плата в отрасли является случайной величиной, распределённой по нормальному закону со средним 13,2 дол. и среднеквадратическим отклонением 2,5 дол. В каком интервале должна быть средняя заработная плата рабочих в компании, имеющей 25 рабочих, чтобы при уровне значимости 0,05 компанию не обвинили в заниженной или завышенной заработной плате?

Варианты ответов: 1) 12,22; 14,18 ; 2) 11,2; 15,2 ; 3) 12, 14,; 4) 11,22; 15,18 .

Решение. Пусть X – ежедневная заработная плата рабочего. Справедливо утверждение, что средняя заработная плата в компании также имеет нормальное распреде-

ление:			xв ~ N 13,2; 2,5 / 5 . Тогда								xв		13,2		~ N 0; 1			, и для уровня значимости 0,05 имеем
ление:			xв ~ N 13,2; 2,5 / 5 . Тогда										0,5		~ N 0; 1			, и для уровня значимости 0,05 имеем
													0,5
		xв	13,2					1,96		13,2 0,98			xв	13,2 0,98						xв 12,22; 14,18 .
		xв	13,2
		0,5
		0,5
	Задание 28. Пусть случайная величина принимает значения -1, 0, 1 с вероятностя-
ми	1			,	1	,	1		соответственно. Тогда точечная оценка величины , полученная ме-
ми				,		,
	3		3					3
тодом наименьших квадратов, равна …
	Варианты ответов: 1) xв ; 2)											1	xв	; 3)		2	xв ; 4)		3	xв .
	Варианты ответов: 1) xв ; 2)										2		xв	; 3)	3		xв ; 4)	2		xв .
											2				3			2

Решение. Так как параметр один, то рассмотрим уравнение, связывающее первые начальные моменты случайной величины X – теоретический и выборочный. Выборочным моментом будет выборочное среднее xв , а теоретическим – математическое

ожидание:

M X		1	1			0	1	1	1				1	1		2	.

					3		3		3					3	3
					3		3		3					3	3
Получаем уравнение	2	x			, откуда ˆ					3	x		.
Получаем уравнение		x		в	, откуда ˆ						x	в	.
3				в					2			в
3									2
Задание 29. Дана выборка пары случайных величин														X ,Y :
		1, 2 ,			0,3 , 1,5 .

Тогда линейное уравнение регрессии, коэффициенты которого вычислены мето-

дом наименьших квадратов, имеет вид …
Варианты ответов: 1) yx 1 x ; 2) yx	10		3	x ; 3) yx	1		3	x ; 4) yx	3 x .

		3	2			3	2

Решение. Линейное уравнение регрессии				имеет	вид:		y a bx .		Идея метода

наименьших квадратов состоит в минимизации суммы квадратов отклонений теоре-

тических значений y xi	от фактических yi :
	3	2 min .
L	a bxi yi	2 min .
	i 1
		22

Это в данном случае равносильно равенству нулю частных производных функции L :

L	3				3	3
	2 a bxi	yi	0,	3 a	xi b	yi ,

i 1

или

i 1

a bx y

i 1

Решая систему линейных уравнений методом Крамера, получим:

	3								3
				yi						xi
				i 1					i	1
	3								3	xi2	3				3		3						3
				xi yi						xi2				yi		xi2		xi							xi yi
a		i 1							i 1			i 1			i 1		i 1						i 1				,

									3						3			3					2


			3							xi
			3							xi			3			x 2			x		i
									i 1							i					i
									i 1						i 1		i	1
			3						3						i 1		i	1
			3						3
				x	i					x 2
					i					i
				i 1					i 1
									3
									3
		3								yi
									i 1
		3							3				3				3		3
				xi					xi yi		3			xi yi			xi						yi
b			i 1						i 1					i 1		i	1		i 1						.

									3				3				3				2


				3						xi
				3						xi			3		x 2			x	i
									i 1							i			i
									i 1					i	1		i 1
				3					3					i	1		i 1
				3					3
				x		i				x 2
						i				i
				i 1					i 1
											3				3								3			3
Из условия задачи получаем:														xi	0,		yi	10,							xi2	2,		xi yi 3 . Далее, под-
												i	1			i 1							i	1			i 1
ставляя это в формулы для коэффициентов, имеем:
				a				10 2 0			10			, b		3 3 0				3		.
				a										, b								.
									3 2	0	3				3 2		0		2
Задание 30. Дана выборка пары случайных величин																									X ,Y :
									1, 2 , 0,3 ,				1,5 .
Тогда оценка ковариации случайных величин X и Y равна …
Варианты ответов: 1) 1; 2) 0; 3) -1; 4) 3.
Решение. Ковариация cov X ,Y												случайных величин X															и Y	определяется равен-
ством cov X ,Y M X							M X			Y	M Y				M X Y						M X					M Y .

Заменяя математические ожидания их оценками (выборочными средними), полу-

чим выражение для оценки ковариации: cov X ,Y							x	y		xв yв . Так как
		1 2 0 3 1 5		1 0 1		2		3	5	10
	x y		1, xв		0, yв							, то cov X ,Y 1 0 1.
		3		3				3			3

					23

Модуль 1. Случайные события

Пример 1. Бросается игральная кость. Найти вероятности следующих событий:

1)А – выпадет пять очков;

2)В – выпадет нечётное число очков;

3)С – выпадет чётное число очков.

Решение. Обратимся к классическому определению вероятности P события,

согласно которому
P	m	,	(1.1)
P	n	,	(1.1)
	n

где n – общее число элементарных исходов эксперимента, а m – число исходов, благоприятных рассматриваемому событию. В данном эксперименте (брошена игральная кость) n 6 (на кости 6 граней). Исходы, что кость упадёт на какое-нибудь ребро или какую-нибудь вершину, отбрасываются как невозможные. Итак, множеством элементарных исходов опыта является конечное множество 1, 2, 3, 4, 5, 6 . Цифра означает возможное число выпавших очков. Все благоприятные исходы какого-нибудь события А будут подмножествами выписанного множества.

В случае события А благоприятным ему исходом является исход 5 ,														то есть m			1.
Следовательно, P A							1		.
Следовательно, P A						6			.
						6
Множеством благоприятных исходов событию В будет множество 1, 3, 5,															, а собы-
тию	С		– множество					2, 4, 6 .		В	каждой	ситуации m 3 . Тогда		P B		3	1	,
тию	С		– множество					2, 4, 6 .		В	каждой	ситуации m 3 . Тогда		P B	6		2	,
															6		2
P C		3		1	.
P C	6		2		.
	6		2
Ответы: 1) P A						1		; 2) P B		1	; 3) P C	1	.
Ответы: 1) P A						6		; 2) P B		2	; 3) P C	2	.
						6				2		2

Пример 2. Бросаются две игральные кости. Найти вероятности того, что сумма выпавших очков:

1)равна десяти,

2)не менее десяти,

3)делится без остатка на три.

Решение. В этом эксперименте (бросаются две игральные кости) элементарными исходами являются возможные пары граней (пары цифр, которые означают число выпавших очков на соответствующих гранях). Из основной теоремы комбинаторики получаем, что n 6 6 36 . Благоприятные исходы к рассматриваемым событиям данного примера будут среди этих 36 элементов. При подсчёте элементарных исходов легко допустить ошибку. Например, студенты говорят, что множеством благоприятных исходов событию А (сумма очков равна 10) будет множество

4,6; 5,5 , что не верно.

Чтобы не допустить ошибку, выпишем все элементарные исходы в виде таблицы (первая цифра которой означает число выпавших очков на первой кости, а вторая – на другой):

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6.2	6,3	6,4	6,5	6,6

Из этой таблицы видно, что множеством благоприятных исходов первому рассматриваемому событию будет множество 4,6; 5,5; 6,4 , то есть m A 3 , и тогда по

формуле (1.1) имеем P A	3		1	.
	36	12

Множество 4,6; 5,5; 6,4; 5,6; 6,5; 6,6 является множеством благоприятствующих исходов событию В: сумма выпавших очков будет не менее 10, то есть равна 10 или

благоприятны событию С: сумма выпавших очков делится на 3 без остатка. Тогда

m С 12 и P C	12		1	.

	36	3
Ответы: 1)	P A	1		; 2)	P B	1	; 3)	P C	1	.

		12				6			3

Пример 3. Акционерное собрание выбирает из 30 человек президента компании, председателя совета директоров и 5 членов совета директоров. Сколькими способами это можно сделать?

Решение. Найдём число способов выбора, используя основную теорему комбинаторики, согласно которой число различных наборов пар объектов будет ровно m n , где m – число объектов типа А, а n – число объектов типа В. Выбрать президента и председателя совета директоров можно 3029 87 способами, так как выбор происходит без повторений и с учётом порядка. Из оставшихся 28 человек можно выбрать

5 в совет директоров	C 5	28!	28	27	26		25	24	98280	способами, так как выбор


	28	5! 23!		2	3	4	5
		5! 23!		2	3	4	5

происходит без повторений и учёта порядка. Поэтому искомое число способов выбора, согласно основной теореме, комбинаторики будет 87 98280 8550360.

Ответ: 8550360 способов.

Пример 4. В очереди стоят 4 женщины и три мужчины. Найти вероятность того, что все женщины стоят рядом.

Решение. В эксперименте (размещение 7 человек в очереди) имеется ровно 7! различных равновозможных исходов, так как производится выборка 7 человек из 7 возможных без повторений и с учётом порядка. Применим классическую схему определения вероятности (с n 7!). Для подсчёта числа благоприятствующих исходов событию А (все женщины находятся рядом) выясним, что возможны всего 4 схемы расположения в очереди: (ж, ж, ж, ж, м, м, м), (м, ж, ж, ж, ж, м, м), (м, м, ж, ж, ж, ж, м), (м, м, м, ж, ж, ж, ж). В каждой такой схеме при учёте порядка мы можем переставлять между собой женщин 4! способами и мужчин – 3! способами. Число благоприятству-

ющих исходов, согласно основной теореме комбинаторики, будет равно 4 4!3!. Тогда,

Пример 5. 4 клиента обращаются в 3 фирмы равновероятно. Найти вероятность, что во все фирмы будут обращения.

Решение. Так как любой из четырёх клиентов может обратиться в любую из трёх фирм, то можно применить для определения вероятности события А (во все фирмы будут обращения) классическую схему (1.1). В данном случае, так как выбор фирм

для обращения клиентами будет производиться с повторениями, то n				34 81. Чтобы
подсчитать			благоприятствующие для А исходы отметим, что	имеется ровно
A3	4!	24	способов размещения обращений четырёх клиентов в три фирмы и 3 схе-


4	1!

мы обращения клиентов в фирмы: (2, 1, 1), (1, 2, 1) и (1, 1, 2). Так как неважно, в ка-

ком порядке обратятся 2 клиента в одну фирму, то						m	3	24	36	. Поэтому (по форму-

								2
								2
ле (1.1)) имеем: P A			36	4	.
ле (1.1)) имеем: P A			81	9	.
			81	9
Ответ: P A	4	.
Ответ: P A	9	.
	9

Пример 6. Из 10 студентов группы, изучающих французский язык, 6 имеют оценку «отлично». Для проверки знаний отобрали четырёх студентов этой группы. Найти вероятность того, что в выборке окажется три студента, имеющих оценку «отлично» по французскому языку.

Решение. Для решения задачи составим схему:

N	10		s	6		N	s	4
k	4		r	3		k	r	1
В этой схеме применены следующие обозначения:					N – число элементов всей со-
вокупности; s	–	число элементов данного качества (свойства), имеющихся во всей
совокупности;	k	– число элементов случайной выборки без возвращения в совокуп-

ность; r – число элементов данного качества, попавших в выборку объёма k . Согласно условию задачи, в таблице расставлены соответствующие значения N, s, k, r , а также значения чисел N s и k r .

Пусть событие А – это r элементов, попавших в выборку объёма k , имеют данное качество. Тогда из классического определения вероятности события вытекает формула

			r	k	r
	P A		Cs	CN	s	,	(1.2)
	P A			CNk		,	(1.2)
				CNk
где символом CMl	обозначается число сочетаний из				M элементов по l		элементов. В
формуле (1.2) n	C Nk есть общее число элементарных исходов, а m						Csr CN s k r –
		26

число исходов, благоприятных событию А (для его вычисления применена основная теорема комбинаторики).

В данном примере событие А состоит в том, что три студента выборки имеют оценку «отлично» по французскому языку. Тогда по (1.2)

								C 3	C1
						P A	6		4	.
						P A				.
								C 4
									10
Так как C 4		10 9 8 7			210 , C 3	6 5 4	20 , C 1				4 , то P A	80	8	.
Так как C 4					210 , C 3		20 , C 1				4 , то P A			.
10		1 2		3 4	6	1 2 3			4			210	21
		1 2		3 4		1 2 3						210	21
Ответ: P	8		0,38 .


	21
Пример 7.	В датчике случайных чисел содержатся все числа из отрезка 0, 100 .
Найти вероятность того, что наугад извлечённое число будет из отрезка													10, 50 .

Решение. Применим геометрическое определение вероятности события. Пусть всем возможным результатам эксперимента соответствуют точки области , а данному собы-

тию А – точки области D, которая является частью области			D	. Тогда
P A	mesD	,		(1.3)
	mes

где mesG – мера множества G (соответственно в одномерном, двумерном, трёхмерном пространствах – это длина, площадь, объём этой области).

В данном примере событие А состоит в том, что выбранное случайно число при-

надлежит отрезку 10, 50 ;	область	– это отрезок 0, 100 , а область D – отрезок
10, 50 . Так как mes 100	0 100,	mesD 50	10 40 (мерами являются длины со-
ответствующих отрезков), то, согласно (1.3), имеем P A				40	0,4 .

				100
				100
Ответ: 0,4.
Пример 8. Имеются два круга радиусов r			10 и r	5 с общим центром. В боль-

шой круг наугад бросается точка. Найти вероятности следующих событий:

1)А – точка попадёт в круг меньшего радиуса;

2)В – точка попадёт в кольцо между окружностями этих радиусов.

Решение. В данном случае необходимо использовать геометрическую схему опре-


деления вероятности, то есть формулу (1.3). В качестве области			имеем круг боль-
шего радиуса. Тогда mes	Sr 10	10 2 100 (мерой круга является его площадь

S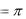r 2 ).

Вслучае события А областью D является круг меньшего радиуса. Тогда

mesD Sr 5	52 25 . Применив формулу (1.3), получим P A					25	0,25 .
mesD Sr 5	52 25 . Применив формулу (1.3), получим P A				100		0,25 .
					100
В случае события В областью D будет кольцо. Тогда
	mesD Sr 10		Sr 5 100 25 75 .
По формуле (1.3) получим P B		75		0,75 .

		100
		100
Обратим внимание, что событие В противоположно событию А. Тогда
		P B	1 P A ,
			27

так как сумма вероятностей противоположных событий равна единице. Так как число

P A было уже найдено, то P B	1 0,25 0,75 . Для вероятности события В получен
тот же ответ.
Ответы: 1) P A 0,25 ; 2) P B	0,75 .

Пример 9. Два теплохода должны подойти к одному причалу. Время прихода обоих теплоходов независимо и равновозможно в течение восьми часов с 8.00 до 16.00. Найти вероятность того, что ни одному из теплоходов не придётся ожидать освобождения причала, если время стоянки первого теплохода – 1 час, а второго – 2 часа.

Решение. Обозначим через x – время прихода первого теплохода, а через y – время прихода второго теплохода. Для того чтобы теплоходы не ожидали освобождения причала, необходимо либо x y 2 , либо y x 1.

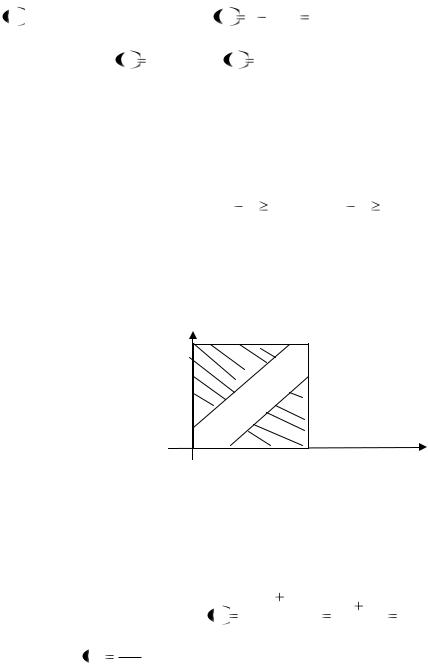
Используем геометрическую схему определения вероятности события А (формулу (1.3)). Изобразим x и y как координаты на плоскости, в качестве единицы масштаба выберем 1 час. Всевозможные исходы представляются точками квадрата со стороной 8, а благоприятствующие событию А располагаются в заштрихованной области (рисунок 4).

0	2	8	x
Рисунок 4 – Рисунок примера 9

Искомая вероятность равна отношению площади заштрихованной фигуры (два равнобедренных прямоугольных треугольника с катетами, равными 6 и 7 соответственно) к площади квадрата:

	1	6	2	1	7	2
P A	2			2			36	49	85	.

			82			128			128

Ответ: P A 12885 .

Пример 10. Первый стрелок поражает мишень в 80 % случаев, а второй – в 60 %. Стрелки сделали по одному выстрелу в мишень. Найти вероятности событий:

1)B0 – оба стрелка промахнутся;

2)B1 – попадёт только один какой-нибудь стрелок;

3)B2 – попадут оба;

4)B – попадёт в мишень хотя бы один из них.

Решение. Решение подобных задач связано с применением понятий алгебры событий, теорем сложения и умножения вероятностей. При этом необходимо знать такие понятия, как зависимые, независимые, совместные и несовместные события.

Введём вспомогательные события: 1) A1 – первый стрелок попадёт в мишень, 2) A2 – второй стрелок попадёт в мишень. По условию имеем: P A1 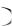0,8; P A2 0,6 (на основе обследования стрелков применено статистическое определение вероятно-

сти случайного события). Введём также противоположные события: A1

– первый

стрелок не попадёт (промахнётся), A2

–

второй промахнётся. Тогда

P A1 0,2 ,

P A2 0,4 (сумма вероятностей противоположных событий равна единице).

Очевидно событийное равенство B0

A2 . Тогда,

ввиду независимости событий,

получим

0,2 0,4 0,08 .

P B0

P A1 A2

P A1

P A2

Событие B1

можно представить как B1

A1 A2

A1 A2 . При этом очевидно, что собы-

тия A1 A2 и A1 A2 не совместны. Применив теорему сложения несовместных событий и

учитывая независимость событий, стоящих в произведениях, получим

0,2 0,6 0,44 .

P B1

P A1

P A2

P A1

P A2

0,8 0,4

Так как B2

A2 , то по теореме умножения вероятностей независимых событий

получим, что P B2

0,8 0,6 0,48 .

Обратим внимание на то, что события B0 , B1 ,

B2 образуют полную группу событий.

Известно, что сумма вероятностей событий, образующих полную группу, равна еди-

нице. Очевидно, что для B0 , B1 , B2

это свойство выполняется:

P B0

P B1

P B2

0,08

0,44

0,48

Вероятность четвёртого события B можно найти различными способами, исполь-

зуя алгебру событий.

Во-первых, из определения суммы событий вытекает равенство B

A2 . Так

как A1 и A2 совместны,

то можно применить теорему сложения вероятностей сов-

местных событий, то есть равенство

P A1

P A2

P A1 A2 .

Тогда P B

0,8 0,6

0,8

0,6

0,92 .

Во-вторых, очевидно равенство

B2 , и по аксиоме сложения вероятностей

несовместных событий B1 , B2

получим

P B

P B1

P B2

0,44

0,48 0,92 .

В-третьих, ясно, что B противоположно B0 . Тогда P B

1 P B0

0,08

0,92 .

Все три способа вероятности события B привели к одному и тому же результату.

Ответы: 1) P B0

0,08 ; 2) P B1

0,44 ; 3)

P B2

0,48 ; 4) P B

0,92 .

Пример 11. Пусть при испытаниях могут иметь место события

A и B , при этом

известно, что P A

0,7 ;

P B

0,5 ;

P AB

0,3 . Найти условные вероятности события

B при условиях, что событие A произошло или не произошло.

Решение.

Так как P A

P B

0,7

0,5

1,2

то события A

и B

совместны.

Справедливы равенства

P A , откуда найдём услов-

P B

P AB

P A

ные вероятности события B по формулам:

P AB

0,3

P A

0,7


P		B	P AB		P B	P AB	0,5	0,3	0,2		2	.
P		B										.
	A		P A	1		P A	1	0,7	0,3	3
			P A	1		P A	1	0,7	0,3	3

Ответы: 1) PA B 73 ; 2) PA B 23 .

Пример 12. Студент выучил 40 вопросов из 50, имеющихся в списке экзаменационных вопросов. В каждый билет преподаватель внёс случайно два вопроса из списка. Найти вероятность того, что студент знает оба вопроса своего билета.

Решение. Пусть A – студент знает первый вопрос своего билета, а B – знает второй вопрос. Тогда AB означает, что он знает оба вопроса. Так как A и B – зависимые события, то по теореме умножения имеем

		P AB P A P B	40	39		156	.
		P AB P A P B					.
		A	50	49	245
			50	49	245
Ответ:	156	.
Ответ:		.
	245

Пример 13. В урне имеются 10 шаров, из которых 6 белые, а остальные – чёрные. Из неё подряд извлекают 3 шара, не возвращая их обратно. Найти вероятность собы-

тия A – все три шара являются чёрными.
Решение.		Для		нахождения			вероятности P A можно	применить	классическое
определение		вероятности и					формулу (1.2). Так как	N 10 , s	4 , k 3, то
P A	C43 C60		4 1	1		.

	C 3	120			30
	10

Другой способ состоит в применении теоремы умножения вероятностей зависимых событий, то есть формулы

P A1 A2 A3	P A1	PA	A2	PA A A3 .		(1.4)
		1		1	2
Для этого введём обозначения событий:		A1	– первый взятый шар является чёрным,
A2 – второй взятый шар чёрный, A3	– третий взятый шар чёрный. Так как шары не

возвращаются, то эти события зависимы, и при этом, согласно определению произве-


дения		событий,					справедливо равенство A A1 A2 A3 . Тогда из (1.4) имеем, что
P A		4		3		2	1		.
P A	10		9		8		30		.
	10		9		8		30
Ответ: P A								1		.
Ответ: P A							30			.
							30

Пример 14. Найти надёжность системы, состоящей из двух последовательно соединённых элементов, работающих независимо друг от друга, при указанной на ри-

сунке 5 надёжности каждого элемента Ai i		1, 2 этой системы.
	A1		A2
	0,9		0,8

Рисунок 5 – Схема соединения системы

Решение. Надёжностью элемента (системы) называют вероятность безотказной работы в течение определённого времени этого элемента (системы).

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20222.72 Mб155660.pdf
#
13.11.20222.72 Mб35661.pdf
#
13.11.20222.72 Mб75662.pdf
#
13.11.20222.81 Mб25663.pdf
#
13.11.20222.82 Mб105664.pdf
#
13.11.20222.86 Mб675665.pdf
#
13.11.20222.89 Mб45666.pdf
#
13.11.20222.92 Mб35667.pdf
#
13.11.20222.96 Mб55668.pdf
#
13.11.20222.96 Mб35669.pdf
#
13.11.20223.01 Mб15670.pdf

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6.2	6,3	6,4	6,5	6,6

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6.2	6,3	6,4	6,5	6,6

1,1	1,2	1,3	1,4	1,5	1,6
2,1	2,2	2,3	2,4	2,5	2,6
3,1	3,2	3,3	3,4	3,5	3,6
4,1	4,2	4,3	4,4	4,5	4,6
5,1	5,2	5,3	5,4	5,5	5,6
6,1	6.2	6,3	6,4	6,5	6,6