5665
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Хабаровский государственный университет экономики и права» Кафедра математики и математических методов в экономике
Теория вероятностей и математическая статистика
Контрольно-измерительные материалы по дисциплине Учебное пособие
Хабаровск 2016
1
ББК В Д 47
Диреев Ю. В. Теория вероятностей и математическая статистика : контрольноизмерительные материалы по дисциплине: учеб. пособие / Ю. В. Диреев, М.Ф. Тиунчик. – Хабаровск: РИЦ ХГУЭП, 2016. – 92 с.
Рецензенты: С. В. Соловьёв, д-р физ.-мат. наук, профессор кафедры прикладной математики Тихоокеанского государственного университета В. И. Чеботарёв, д-р физ.-мат. наук, завлабораторией
приближённых методов и функционального анализа ВЦ ДВО РАН
Утверждено издательско-библиотечным советом университета в качестве учебного пособия для студентов и бакалаврантов
© Хабаровский государственный университет экономики и права, 2016
2
Предисловие
Учебное пособие предназначено для бакалаврантов всех профилей, обучающихся по направлению «Экономика» и изучающих математику отдельными базовыми дисциплинами, к которым относится и фундаментальная дисциплина – теория вероятностей и математическая статистика.
По учебному плану дисциплина изучается на втором курсе. В соответствии с государственным образовательным стандартом третьего поколения основной упор делается на самостоятельную работу студента и его индивидуальное общение с преподавателем. На аудиторную работу (лекции и практические занятия) отводится только 72 часа в течение всего учебного года. В связи с этим особое значение приобретают самоконтроль и контроль знаний преподавателем.
Пособие предназначается для проведения тестового контроля знаний в различных формах и для подготовки студентов к такому контролю. Первой обязательной формой контроля в Хабаровском государственном университете экономики и права является промежуточная аттестация студентов, которая проводится в середине каждого семестра. Кроме того, при необходимости кафедрой проводится контроль знаний и по отдельным разделам дисциплины. Завершающими формами контроля являются: зачёт по материалу первого семестра и экзамен по всем темам дисциплины в весеннюю сессию.
Для окончательного контроля знаний по всей дисциплине в пособии приведены два тестовых задания, каждое из которых состоит из 30 примеров. Первое из них служит для самостоятельной проверки знаний; решения примеров не приводятся; предлагается четыре варианта ответов, только один из которых является правильным. Во втором задании с вариантами ответов даны краткие решения примеров, типы которых отличаются от примеров первого задания. Оба задания затрагивают все основные понятия, утверждения и методы дисциплины. По этим двум образцам преподаватели готовят типовые аттестационные задания для каждого студента. При упомянутых промежуточных аттестациях используется часть заданий, затрагивающая изученные к тому времени темы дисциплины.
Основной материал дисциплины (тематическое наполнение содержания АПИМ – аттестационные педагогические измерительные материалы) изложены в наборах возможных заданий (без вариантов ответов) с подробными решениями и теоретическими пояснениями. Эти наборы разбиты на три модуля: 1) случайные события, 2) случайные величины, 3) математическая статистика. В модулях приведены решения 105 упражнений. Аналогичные примеры могут быть использованы для формирования аттестационных заданий. В пособии при решении примеров используются 22 рисунка. Нумерация рисунков в работе сплошная, через все модули. Формулы же нумеруются отдельно в каждом модуле. Например, формула 15 из модуля 2 обозначается как (2.15), а формула 21 из модуля 3 нумеруется как (3.21).
3
Изучение модулей не предполагает предварительных знаний по дисциплине. При решении примеров приведены основные теоретические положения. В случае затруднений надо обращаться к соответствующим темам рекомендуемой литературы.
Тематическое наполнение модулей следующее. В первом модуле содержатся определение вероятности, классическая схема, теоремы умножения и сложения вероятностей, формулы полной вероятности и Байеса, повторные независимые испытания, приближённые формулы в схеме Бернулли. Во втором модуле приведены примеры на законы распределения вероятностей дискретных и непрерывных случайных величин, на вычисление числовых характеристик случайных величин и их свойства. Также рассмотрены задачи, при решении которых используются важнейшие теоретические законы, законы больших чисел. В третьем модуле даны примеры на статистические распределения выборки, числовые характеристики выборки, точечные и интервальные статистические оценки, оценки математического ожидания и дисперсии, оценки параметров теоретических законов распределения. Кроме того, элементы корреляци- онно-регрессионного анализа, проверка статистических гипотез отражены в соответствующих примерах этого модуля.
Авторы надеются, что структура пособия позволит применять многоуровневую подготовку. При подготовке к аттестации любой формы студент должен самостоятельно выполнить примеры соответствующей тематики первого тестового задания. При неуспехе необходимо перейти к примерам соответствующей тематики тестового материала второго уровня – заданиям с вариантами ответов и решениями. В случае необходимости и для более глубокого изучения предмета надо переходить к изучению материала третьего уровня – обучающих примеров перечисленных модулей. Обращение к соответствующим модулям возможно и при проблемах с решениями примеров по отдельным разделам дисциплины.
Примеры, рассмотренные в модулях пособия, дают возможность преподавателям, ведущим занятия по данной дисциплине, подобрать задания для самостоятельной работы студентов и для контрольных мероприятий. Такая возможность возникает из того, что примеры в модулях имеют различные уровни трудоёмкости.
Пособие может быть использовано для подготовки к интернет-экзамену, который проводится при государственной аттестации образовательных направлений и профилей обычно на старших курсах обучения.
В заключение отметим, что пособие вместе с аналогичными пособиями [15], [16] позволяет преподавателям проводить аттестацию студентов в различных формах по основным математическим дисциплинам (линейная алгебра, математический анализ, теория вероятностей и математическая статистика), вести по ним многоуровневую подготовку, своевременно выявлять слабо усвоенные студентами темы и производить соответствующую корректировку учебного процесса.
4
Тестовые задания для самостоятельной работы
Задание 1. Брошены две игральные кости (игральная кость – шестигранный кубик). Вероятность того, что на обеих костях будет одинаковое число очков, равна …
Варианты ответов: 1) 12 ; 2) 361 ; 3) 16 ; 4) 13 .
Задание 2. В первой урне имеются 5 белых и 5 красных шаров, а во второй – 4 белых и 6 красных. Выбирающий наугад берёт из каждой урны по одному шару. Вероятность того, что оба шара будут красного цвета, равна …
Варианты ответов: 1) 12 ; 2) 53 ; 3) 10011 ; 4) 103 .
Задание 3. В корзине находятся 10 яблок и 5 груш. Из неё наугад достают четыре фрукта. Вероятность, что в выборке будет 2 яблока и 2 груши, равна …
Варианты ответов: 1) 13 ; 2) 3091 ; 3) 12 ; 4) 109 .
Задание 4. В коробке лежат 4 чёрных и 6 белых однотипных шаров. Из неё достают 3 шара подряд, не возвращая их обратно. Вероятность, что все три шара белые, равна …
Варианты ответов: 1) 16 ; 2) 103 ; 3) 12 ; 4) 23 .
Задание 5. На пяти одинаковых карточках написана одна из букв А, Г, И, К, Н. Ученик случайно берёт по одной карточке и расставляет их в одну линию. Вероятность образования слова «книга» равна …
Варианты ответов: 1) 15 ; 2) 1201 ; 3) 1; 4) 241 .
Задание 6. Первый стрелок поражает цель в 80 % случаев, второй – в 60 %. Стрелки сделали по одному выстрелу. Вероятность того, что попал только один какойнибудь стрелок, равна …
Варианты ответов: 1) 0,48; 2) 0,92; 3) 0,2; 4) 0,44.
Задание 7. Студент добирается на занятия в половине случаев на автобусе, а в половине случаев на трамвае. Вероятность опоздания на занятия при поездке на автобусе равна 0,06, а при поездке на трамвае – 0,03. Вероятность опоздания им на занятия в отдельный случайный день поездки равна …
Варианты ответов: 1) 0,045; 2) 12 ; 3) 0,0018; 4) 0,09.
Задание 8. Вероятность выпадения орла все 5 раз при пяти бросаниях монеты равна …
Варианты ответов: 1) 12 ; 2) 15 ; 3) 321 ; 4) 1.
5
Задание 9. Приживаемость саженцев данной культуры при посадке составляет 80 %. Наиболее вероятное число прижившихся при посадке 400 штук таких саженцев будет …
Варианты ответов: 1) 320; 2) 80; 3) 32; 4) 160.
Задание 10. За некоторое время до отправления электропоезда к автомату за покупкой билета в минуту подходило в среднем 3 пассажира. Вероятность того, что в
течение двух минут подходят не менее двух пассажиров, равна … |
|
|
||||||||||||||||||||||
|
Варианты ответов: 1) e 3 ; 2) 1 7e 6 ; 3) 1 |
e 6 ; 4) 1 6e 6 . |
|
|
|
|
|
|||||||||||||||||
|
Задание 11. Закон распределения дискретной случайной величины X имеет вид: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
-2 |
|
|
|
-1 |
|
|
1 |
|
|
|
2 |
|
||||||
|
|
P |
|
|
|
0,15 |
|
|
0,20 |
|
|
|
p3 |
|
|
|
0,25 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда вероятность p3 |
появления значения x3 |
1 равна … |
|
|
|
|
|
|||||||||||||||||
|
Варианты ответов: 1) 0,25; 2) 0,20; 3) 0,50; 4) 0,4. |
|
|
|
|
|
||||||||||||||||||
|
Задание 12. Функция распределения |
F x |
|
дискретной случайной величины X |
||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
при |
x |
10; |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0,15 |
при |
10 |
|
x |
15; |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F x |
0,45 |
при |
15 |
|
x |
20; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0,55 |
при |
20 |
|
x |
30; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0,8 |
при |
30 |
|
x |
35; |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
при |
x |
35. |
|
|
|
|
|
|
|
|
|
||||
Тогда распределением этой случайной величины является ряд … |
|
|
||||||||||||||||||||||
|
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X |
|
|
0 |
|
|
10 |
|
|
15 |
|
20 |
|
30 |
|
35 |
|
||||||
|
|
P |
|
|
0 |
|
|
0,15 |
|
|
0,45 |
|
0,55 |
|
0,8 |
|
1 |
|
||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X |
|
10 |
|
|
|
15 |
|
|
|
20 |
|
|
30 |
|
|
35 |
|
|||||
|
|
P |
|
0,15 |
|
|
0,45 |
|
|
|
0,55 |
|
|
0,25 |
|
|
1 |
|
||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X |
|
10 |
|
|
|
15 |
|
|
|
20 |
|
|
30 |
|
|
35 |
|
|||||
|
|
P |
|
0,15 |
|
|
0,30 |
|
|
|
0,10 |
|
|
0,25 |
|
|
0,20 |
|
||||||
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X |
|
10 |
|
|
|
15 |
|
|
|
20 |
|
|
30 |
|
|
35 |
|
|||||
|
|
P |
|
0,20 |
|
|
0,25 |
|
|
|
0,10 |
|
|
0,30 |
|
|
0,15 |
|
||||||
|
Задание 13. Функция распределения |
F x непрерывной случайной величины |
||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
при |
x |
1, |
|
F x |
1 |
x 2 |
x |
при 1 |
x |
2, |
|
2 |
|||||||
|
|
|
|
|
|
||
|
|
1 |
|
при |
x |
2. |
Тогда плотностью распределения (дифференциальной функцией) является функция f x
…
Варианты ответов:
|
|
|
|
0 |
|
|
|
при |
|
x |
1, |
|
1) |
f |
x |
x3 |
x 2 |
|
при |
|
1 |
x 2, ; |
|||
|
|
|
|
0 |
|
|
|
при |
|
x |
2. |
|
|
|
|
|
0 |
|
|
|
при |
|
x |
1, |
|
2) |
f |
x |
x |
1 |
|
при |
1 |
x |
2, ; |
|||
|
|
|
|
|||||||||
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
при |
|
x |
2. |
|
|
|
|
0 |
|
|
при |
x |
|
1, |
|
||
3) |
f |
x |
x |
|
|
при |
1 |
x |
2, ; |
|||
|
|
|
1 |
|
|
при |
x |
|
2. |
|
||
|
0 |
при |
x |
1, |
4) f x |
2x 1 |
при 1 |
x |
2, . |
|
0 |
при |
x |
2. |
Задание 14. Случайная величина задана плотностью распределения;
|
0 |
при |
x |
2, |
|
f x |
1 |
при 2 |
x |
10, |
|
|
|||||
8 |
|||||
|
|
|
|
||
|
0 |
при |
x |
10. |
Тогда её функция распределения F x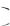
имеет вид …
Варианты ответов:
|
|
0 |
|
при |
|
x |
2, |
|||||
1) F x |
1 |
x |
1 |
при |
2 |
x |
10, ; |
|||||
|
|
|||||||||||
|
|
8 |
|
|
|
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
при |
|
x |
10. |
|||||
|
|
0 |
при |
x |
|
2, |
|
|||||
2) |
F x |
|
1 |
x |
при |
2 |
x |
10, ; |
||||
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
при |
x |
10. |
|
||||||
|
|
0 |
при |
x |
2, |
|
||||||
3) |
F x |
|
|
1 |
x |
при |
2 |
x |
10, ; |
|||
8 |
||||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
1 |
при |
x |
|
10. |
|
|||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
0 при x 2,
4) F x 8x при 2 x 8, .
1 при x 8.
Задание 15. Непрерывная случайная величина задана функцией распределения:
|
|
|
0 |
при |
x |
2, |
|
F x |
|
1 |
x 2 2x |
при |
2 |
x 5, |
|
15 |
|||||||
|
|
|
|
|
|||
|
|
|
1 |
при |
x |
5. |
|
Тогда вероятность P 0 X |
4 |
равна … |
|
|
|||
Варианты ответов: 1) 13 ; 2) 0; 3) 158 ; 4) 151 .
Задание 16. Плотность распределения имеет вид:
|
|
|
0 |
при |
x |
0, |
||
f x |
|
1 |
|
x2 |
при 0 |
x |
6, |
|
12 |
||||||||
|
|
|
|
|
||||
|
|
|
0 |
при |
x |
6. |
||
Тогда вероятность P 2 |
X |
4 |
равна … |
|
|
|
|||||
Варианты ответов: 1) |
|
1 |
; 2) |
|
1 |
; 3) |
2 |
|
; 4) |
8 |
. |
72 |
2 |
9 |
|
27 |
|||||||
|
|
|
|
|
|
||||||
Задание 17. Ряд распределения дискретной случайной величины имеет вид:
|
|
Х |
|
|
|
|
|
-2 |
|
|
1 |
|
|
|
Р |
|
|
|
|
|
0,6 |
|
|
0,4 |
|
Тогда математическое ожидание M X |
и дисперсия D X равны … |
|||||||||||
Варианты ответов: 1) M X |
1,2, |
D X |
1,44; |
|
||||||||
2) M X |
0,8, D X |
2,16; 3) M X |
0,4, |
D X 0,16; 4) M X 1,6, D X 2,8. |
||||||||
Задание 18. Плотность распределения имеет вид: |
||||||||||||
|
|
|
0 |
при |
x |
0, |
|
|
|
|||
|
|
f x |
|
1 |
x |
при |
0 |
x |
4, |
|
|
|
|
|
8 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
при |
x |
10. |
|
|
||||
Тогда дисперсия случайной величины равна …
Варианты ответов: 1) 89 ; 2) 83 ; 3) 8 ; 4) -2.
8
Задание 19. График функции F x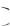
распределения вероятностей имеет вид:
y |
|
y |
|
F x |
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
2 |
|
6 |
|
x |
|
|
||
Рисунок 1 – График функции распределения F x |
|
|
|||||||
Тогда математическое ожидание M X и дисперсия D X |
равны … |
|
|
||||||
Варианты ответов: |
1) M X |
4, D X |
2 ; |
2) M X 4, D X |
4 |
; |
|||
3 |
|||||||||
|
|
|
|
|
|
|
|
||
3) M X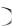 
2, D X 
4 ; 4) M X 
6, D X 
4 .
Задание 20. Непрерывная случайная величина распределена по нормальному за-
кону с математическим ожиданием M X |
50 и средним квадратическим отклонени- |
|||||||||||||||||||||||||||||||
ем |
X |
5 . |
Тогда для вероятности события 40 |
X |
60 , записанной с помощью |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функции Лапласа |
x |
|
|
e |
2 dt , получим ответ … |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Варианты |
|
ответов: |
|
|
1) |
60 |
40 ; |
|
2) |
|
12 |
8 ; |
3) |
2 |
2 ; |
|||||||||||||||||
4) |
40 |
10 |
|
60 |
10 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задание 21. Случайные величины X , Y , Z, V независимы, одинаково распределе- |
||||||||||||||||||||||||||||||||
ны, с математическим ожиданием, равным нулю, и дисперсией, равной |
2 . Тогда ма- |
|||||||||||||||||||||||||||||||
тематическое ожидание и дисперсия определителя |
|
X |
Y |
|
равны … |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
V |
|
|
|
|
|
|
|
|
Варианты |
|
|
ответов: |
1) |
|
|
M |
0, D |
0 ; |
2) |
M |
0, D |
2 |
2 ; |
||||||||||||||||||
3) M |
|
0, D 2 4 ; 4) M 1, D |
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Задание 22. Дискретный статистический ряд с вариантами |
xi и их частотами ni |
|||||||||||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xi |
|
|
|
5 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
20 |
|
|
30 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ni |
|
|
|
10 |
|
|
|
|
|
|
20 |
|
|
|
|
|
n3 |
|
|
5 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Причем объём выборки n |
50 . Тогда относительная частота w3 значения x3 |
20 равна … |
||||||||||||||||||||||||||||||
Варианты ответов: 1) |
|
3 |
; 2) |
2 |
; 3) 15 |
; 4) |
13 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
5 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
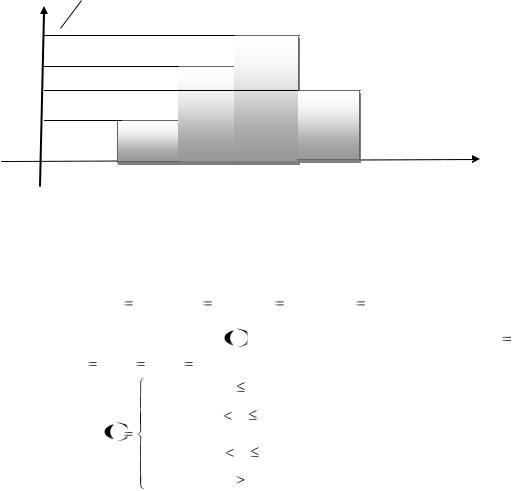
Задание 23. Гистограмма частот интервальной выборки имеет вид:
ni h
20
15
10
5
0 |
2 |
4 |
6 |
8 |
10 |
xi |
Рисунок 2 – Гистограмма интервальной выборки (по вертикальной оси применён другой масштаб)
Тогда частота n4 значений, попавших в четвёртый промежуток (от 8 до 10), равна …
Варианты ответов: 1) n4 |
10 ; 2) n4 |
8 ; 3) n4 20 ; 4) n4 2 . |
|||||||||||
Задание 24. Эмпирическая функция Fn |
x |
распределения выборки объёма n 20 с |
|||||||||||
вариационным рядом x1 |
2, x2 |
|
4, x3 8 |
имеет вид: |
|||||||||
|
|
|
|
|
0 |
|
при |
|
x |
2, |
|
||
|
|
|
|
|
1 |
|
при |
2 |
x |
4, |
|||
|
|
|
|
|
|
|
|
||||||
|
|
Fn |
x |
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
при |
4 |
x |
8 |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
при |
|
x |
8. |
|
||
Тогда её статистическим рядом с частотами ni будет… |
|||||||||||||
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
2 |
|
|
4 |
|
|
|
|
8 |
|
|
|
|
ni |
2 |
|
|
8 |
|
|
|
|
10 |
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
2 |
|
|
4 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ni |
5 |
|
|
10 |
|
|
|
5 |
|
|
||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
0 |
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
2 |
|
|
8 |
|
|
|
|
10 |
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
0 |
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ni |
5 |
|
|
10 |
|
|
|
5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|