4959

20

слишком много, а с учётом тех, которые влияют на них, теория становилась многофакторной и слишком сложной, поэтому А. Маршалл не включил её в конечный вариант «Принципов экономической науки».

Теория экономического роста развивалась в форме абстрактных моделей, обосновывающих взаимосвязь и взаимозависимость основных факторов производства и темпов его расширения. Стимул в создании такой теории – необходимость государственного регулирования роста рыночной экономики. И если сам Дж. М. Кейнс не рассматривал проблемы долгосрочного экономического роста, то его исследования послужили основанием для появления кейнсианского варианта теории экономического роста. Попытка формализовать условия экономического роста привела в 1930-е гг. к появлению моделей роста, первой из которых считается модель Харрода – Домара

2.2. Модель Харрода – Домара Англичанин Рой Харрод (1900 – 1978) и американец Евси Домар (1914 – 1997) почти одновременно разработали концепцию экономического роста в конце 30-х – 40-е гг. ХХ века. В основе её лежат две предпосылки.

Первая – рост общего выпуска определяется только одним фактором – долей инвестиций в национальном доходе. Все остальные факторы: увеличение занятости, степень использования оборудования, улучшения в организации производства, – отражающиеся на росте капиталоотдачи (У/К), исключаются.

Тогда и спрос на капитал при данной капиталоёмкости (k=К/У) или капиталоотдаче (1/k=У/К) определяется только темпом роста национального дохода.

Вторая предпосылка: сама капиталоёмкость не зависит от соотношения цен на факторы производства. Она определяется лишь техническими условиями производства, которые сохраняют её неизменной вследствие неизменного

21

Связь между долей инвестиций в национальном доходе и капиталоёмкостью

Левая часть равенства (2.7) не что иное как темп роста валового продукта, т.е. темп роста экономики.

Поскольку в условиях равновесия I = S , а S = sY , темпы роста объёма выпуска и национального дохода равны темпам роста инвестиций:

∆У /У =∆ I /I = s / k.

Выражение (2.7) – это упрощённая форма известного уравнения из теории экономического роста Харрода – Домара, из которого следует, что темп роста валового продукта (и национального дохода) находится в прямой зависимости от нормы сбережений и в обратной – от коэффициента капиталоёмкости.

Основной акцент в модели сделан на темпы роста национальных сбережений, определяющих в конечном итоге и темпы экономического роста, и объёмы инвестиций в национальную экономику. Длительное время этот тезис являлся фундаментальным при разработке национальной экономической политики. Представление о том, что рост пропорционален инвестициям, не ново. Е. Домар заметил, что более раннее поколение экономистов, крайне озабоченных вопросами роста, – советские экономисты 1920-х гг. – уже использовали ту же идею.

Таким образом, рецепт развития был крайне прост: наращивание объёма сбережений. Специалисты по развитию считали, что бедные страны настолько бедны, что у них нет особых надежд на рост объёма собственных сбережений. Это приводило к несоответствию между «требуемыми инвестициями» и реальным уровнем национальных сбережений. Существующий «дефицит финансирования» в этом случае должны заполнить западные доноры, что приведёт к достижению требуемого объёма инвестиций и, в свою очередь, обеспечит достижение целевых показателей экономического роста.

22

Экономисты, защищавшие данный подход, не очень хорошо понимали, сколько времени понадобится на то, чтобы помощь привела к увеличению инвестиций и, соответственно, к увеличению темпов роста. Но на практике они ожидали быстрых результатов: помощь этого года пойдёт на инвестиции этого же года, что отразится на росте ВВП в следующем году

В развивающихся странах модель роста Харрода – Домара была применена впервые при определении темпов роста первого пятилетнего плана Индии 1951 – 1956 гг. Модель была подвергнута некоторой модификации американским экономистом Х.Б. Зингером. Вскоре стало очевидным, что даже с учётом внесённых уточнений, с её помощью невозможно обеспечить качественный прогноз на будущее и тем более использовать её как инструмент для выработки экономической политики.

Основные выводы модели легли в основу теорий «большого толчка» («big push») и перехода к «самоподдерживающемуся росту». Достижение нормы накопления, достаточной для поддержания целевого темпа роста в будущем символизирует собой переход страны к «самоподдерживающемуся росту». Выводы модели широко использовались, в частности, для расчёта необходимых ресурсов, получаемых в качестве помощи от иностранных государств. Эту модель позже называли моделью «дефицита сбережений». Один из существенных недостатков модели состоит в том, что анализ факторов роста ограничен капиталом и из поля зрения выпадают естественные и трудовые ресурсы.

2.3. Модель экономического роста с двумя дефицитами. Дальнейшее совершенствование модели «дефицита сбережений» шло как в направлении её детализации и уточнения в соответствии с особенностями развивающейся экономики (учёта внешнеэкономических связей и т.п.), так и по пути разработки моделей для более низких уровней экономики развивающихся стран: секторного и отраслевого.

Модель экономического роста с двумя дефицитами (two gaps model) была разработана в 60 – 70-е гг. группой американских исследователей – X. Ченери, М. Бруно, А. Страутом, П. Экстейном, Н. Картером и др. Она представляет собой систему средне- и долгосрочных регрессивных моделей, в которых темп роста определяется в зависимости от дефицита внутренних (дефицит сбережений) либо внешних (торговый дефицит) ресурсов. Модель включает три основных элемента: во-первых, расчёт необходимых ресурсов, получаемых как разность сбережений (S) и инвестиций (I); во-вторых, вычисление внешнеторгового дефицита: экспорт (X) минус импорт (М); в-третьих, определение абсорбционной (поглотительной) способности, понимаемой как

23

максимальный объём капитальных ресурсов, которые развивающаяся страна способна производительно использовать в данный момент. Поэтому в статике модель можно записать следующим образом:

внутренние сбережения, I – валовые внутренние инвестиции, X – экспорт, М – импорт.

Разница между валовыми внутренними инвестициями и валовыми внутренними сбережениями может быть компенсирована иностранной

Объём иностранной помощи для обеспечения предусмотренного политикой модернизации заданного целевого темпа роста определяется наибольшим из этих двух дефицитов. Помощь осуществляется не только для того, чтобы уменьшить внутренний и внешний дефициты, но и для того, чтобы с течением времени либо вообще отказаться от иностранной помощи, либо значительно снизить её величину.

Проделанный X. Ченери и А. Страутом анализ 50 развивающихся стран показал, что средние темпы прироста сбережений составили в 1957 – 1962 гг. 6 – 8%, а максимальные – 12 – 15%. Эти последние и были приняты в качестве абсорбционной способности стран «третьего мира». Максимальные темпы прироста сбережений обеспечивали при этом ежегодный темп прироста ВНП на уровне 5 – 7%. Поэтому в

возможный темп роста инвестиций; k – приростный капитальный коэффициент (IСОR); α – предельная норма сбережений или предельная склонность к сбережениям (α = ∆Ŝ/∆У, где ∆Ŝ – потенциальные внутренние сбережения).

24

Предполагается, что первая стадия модернизации закончится тогда, когда темп роста инвестиций сравняется с темпом роста ВНП. Допустим, что это произойдёт в момент времени t = т. Тогда Iт = k řУт , где ř – целевой темп роста ВНП.

В зависимости от того, какой именно дефицит преобладает, наступает вторая или третья стадия модернизации.

Компенсировать нехватку внутренних сбережений может импорт иностранных товаров и услуг, однако целью данной стадии модернизации является обеспечение таких условий, при которых этот приток должен постепенно уменьшаться. Это достигается при α' > k ř, тогда S= I, М→ 0, где М – требуемый объём импорта товаров и услуг.

Для ликвидации внешнеторгового дефицита необходимо перераспределить внутренние инвестиции таким образом, чтобы этот дефицит был ликвидирован. Допустим, что третья стадия модернизации начнется в момент времени t= п. Тогда

где μ' – предельная склонность к импорту (μ' = ∆М/∆У); х – темп роста экспорта, рассчитанный экзогенно (характеризует меры государства по стимулированию экспорта).

Дефицит торгового баланса будет ликвидирован, если х > ř, а μ'< μср, где μср – средняя склонность к импорту. Достаточный объём сбережений находится как

Рост объёма потенциальных сбережений не только обеспечит внутренние потребности в капиталовложениях, но и позволит со временем полностью отказаться от иностранной помощи (если Ŝ > I ).

Решая проблему нехватки сбережений, экономика одновременно избавляется от торгового дефицита и, наоборот, решая проблему нехватки торгового дефицита, одновременно решает проблему дефицита сбережений. Всё зависит в конечном счёте от правильного выбора целевого темпа роста ВНП и мер, которые обеспечивают его достижение. Поэтому существует такая точка, в которой стратегии пересекаются, она и определяет целевой темп роста ВНП.

Описанная модель модернизации была разработана для Израиля. В дальнейшем она была значительно усовершенствована и широко применялась для определения размеров иностранной помощи в странах Азии и Латинской Америки. В 1972 г. X. Ченери и Н. Картером была осуществлена корректировка модели с целью показать влияние прироста иностранных ресурсов и экспорта на

25

размеры внутренних сбережений. Поэтому формула для определения

где Ŝ1, – предельная склонность к сбережениям; Ŝ2, Ŝ 3 – коэффициенты, отражающие влияние прироста иностранных ресурсов (F) и экспорта (X) на размер внутренних сбережений (S).

По принципу теоретической модели с двумя дефицитами в 70-е гг. было

Модель с двумя дефицитами есть дальнейшая конкретизация идеи «большого толчка». Её цель – проследить взаимосвязь развития внутреннего накопления и внешних источников финансирования. Она явно недооценивала внутренние ресурсы развивающихся стран, что объективно вело к завышению потребности в иностранной помощи и в конечном счёте – к стремительному росту внешнего долга. Усиление внешнеэкономической зависимости вызвало резкую критику кейнсианской модели со стороны леворадикальной политической экономии.

Рассмотренные модели экономического роста были ориентированы на использование такого ограниченного в развивающихся странах фактора, как капитал, и явно не учитывали возможности использования такого относительно избыточного фактора, как труд. Это и определило справедливую критику неокейнсианского направления со стороны неоклассиков.

Ещё одним заметным недостатком этой модели является фактическое обоснование вмешательства стран-доноров во внутренние дела страндолжников. Существенным недостатком оказался весьма агрегированный (приблизительный) характер модели. В условиях ограниченности и ненадёжности статистической информации многие важные показатели модели (например, определение абсорбционной способности экономики развивающихся стран) носят чрезвычайно условный характер, что снижает ценность полученных

сих помощью прогнозов и рекомендаций.

2.4.Модель Р.Солоу. В 1950-е гг. было обращено внимание на тот факт, что модель Харрода – Домара позволяет описать лишь краткосрочный экономический рост, поскольку в долговременной перспективе рост ВНП ограничивается темпами роста населения (или рабочей силы). Реакцией на это открытие явилось создание в 1957 г. американским экономистом лауреатом Нобелевской премии Робертом Мертоном Солоу (р. 1924), неоклассической

27

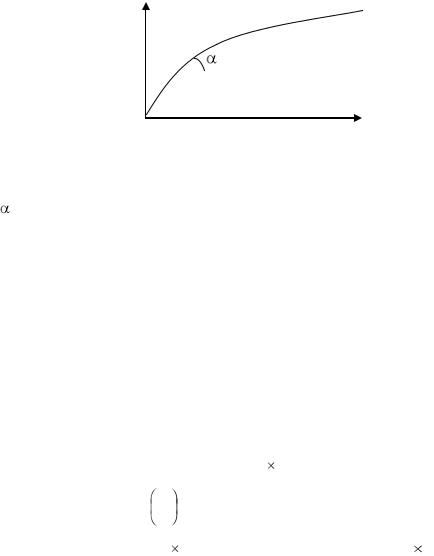
капиталовооружённостью. Построим график этой производственной функции

(рисунок 2.4.1):

Рисунок 2.4.1 – Производственная функция

предельной производительностью капитала.

Солоу упрощает анализ экономики, предполагая, что нет государства и внешней торговли. Тогда спрос на произведённый продукт – это спрос со стороны домохозяйств (потребителей) и фирм (инвесторов), то есть продукция, произведённая каждым работником делится между потреблением и инвестициями, в

Таким образом, инвестиции (как и потребление) пропорциональны доходу. Если i = s, норма сбережений s также показывает, какая часть произведённой

продукции направляется на капиталовложения.

Представив две главных составляющих модели Солоу – производственную функцию и функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост.

Запасы капитала могут меняться по двум причинам:

-инвестиции приводят к росту запасов капитала;

-часть капитала изнашивается, то есть амортизируется, что приводит к уменьшению запасов капитала.

28

Инвестиции в расчёте на одного работника i = sy, а y = f(k), тогда i = s f(k). Отсюда, чем выше уровень капиталовооружённости (k), тем выше объём производства f(k) и больше инвестиции (i).

Представим графически (рисунок 2.4.2): f(k)

y

c

sf(k)

y

i

0 k k

Рисунок 2.4.2 – Производство, потребление и инвестиции

Хорошо видно, как норма сбережений (s) определяет разделение продукта на потребление и инвестиции для каждого из значений капиталовооружённости.

Чтобы учесть в модели амортизацию, предполагаем что ежегодно выбывает

графика видно, что выбытие пропорционально запасам капитала (рисунок 2.4.3). Тогда изменение запасов капитала на 1 работника ( k)

Рисунок 2.4.3 – Инвестиции, выбытие и устойчивый уровень капиталовооружённости

В точке А выбытие капитала компенсируется инвестициями 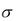k = s f(k), поэтому k* – единственный уровень капиталовооружённости, который не будет

29

меняться во времени. Тогда k* – устойчивая капиталовооружённость. Устойчивый уровень капиталовооружённости соответствует равновесию экономики в долгосрочном плане. Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она достигает затем устойчивого состояния. Докажем это.

Пусть k1 < k*, при k1, как видно на графике i1 > 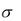k1, следовательно капиталовооружённость растёт, что приводит к росту производства до тех пор, пока не приблизится к устойчивому уровню капиталовооружённости (k*).

При k2 > k* всё будет происходить наоборот.

Таким образом, если экономика не находится в устойчивом состоянии, то независимо от размера капитала на одного работающего начинают действовать силы, приводящие её к долгосрочному устойчивому равновесию. Параметр, обеспечивающий равномерный рост в модели Солоу – капиталовооружённость труда. Динамические системы, в которых переменные обладают свойством автоматически возвращаться к состоянию устойчивого равновесия, называются стабильными системами. То есть модель роста Солоу описывает стабильный динамический процесс роста.

Может ли более высокий уровень сбережений обеспечить высокий экономический рост?

Рассмотрим, что происходит в экономике с изменением нормы сбережений. Пусть норма сбережений (S) растёт с S1 до S2 (рисунок 2.4.4)

k

i k S2 f(k) = i2 S1 f(k) = i1

инвестиции больше выбытия (Ii > k1), что приводит к росту капитала до тех пор, пока экономика не достигает нового устойчивого состояния k c большей капиталовооружённостью и более высокой производительностью труда, чем в исходном периоде.