Однородные уравнения с постоянными коэффициентами
Схема решения
Составим характеристическое уравнение
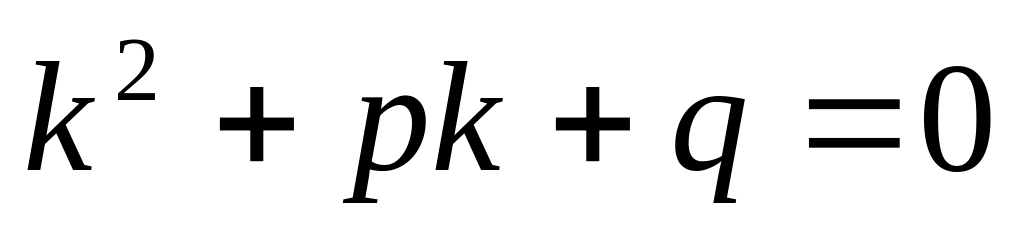и найдём его дискриминант
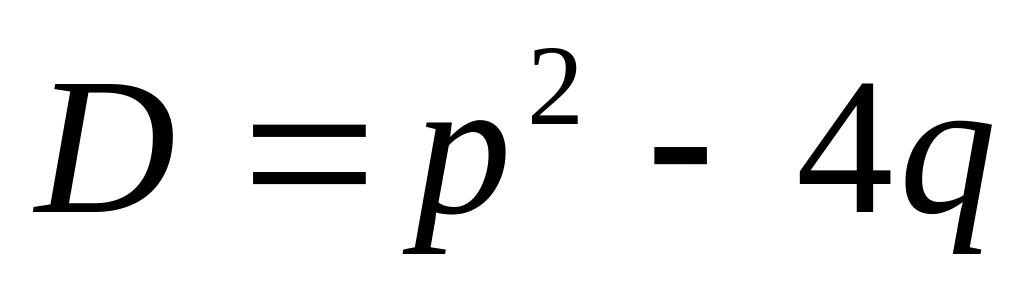;Если
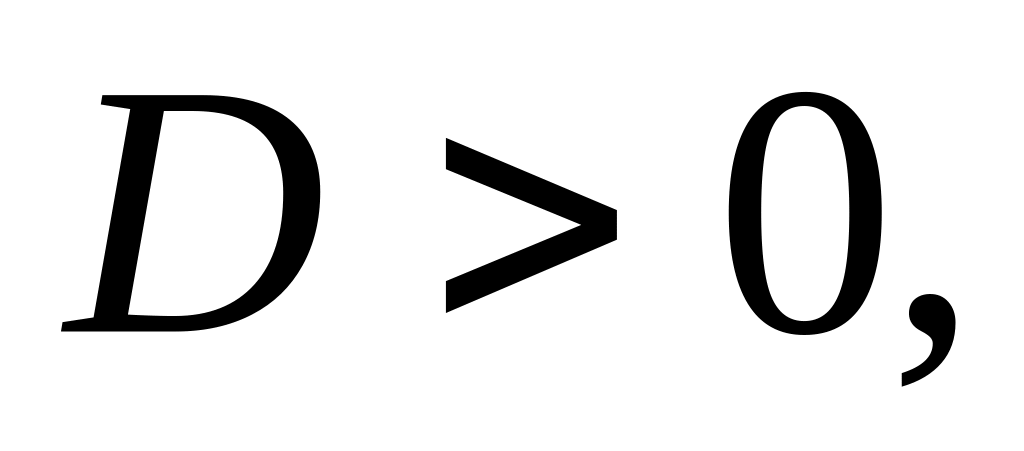уравнение имеет 2 действительных корня
,
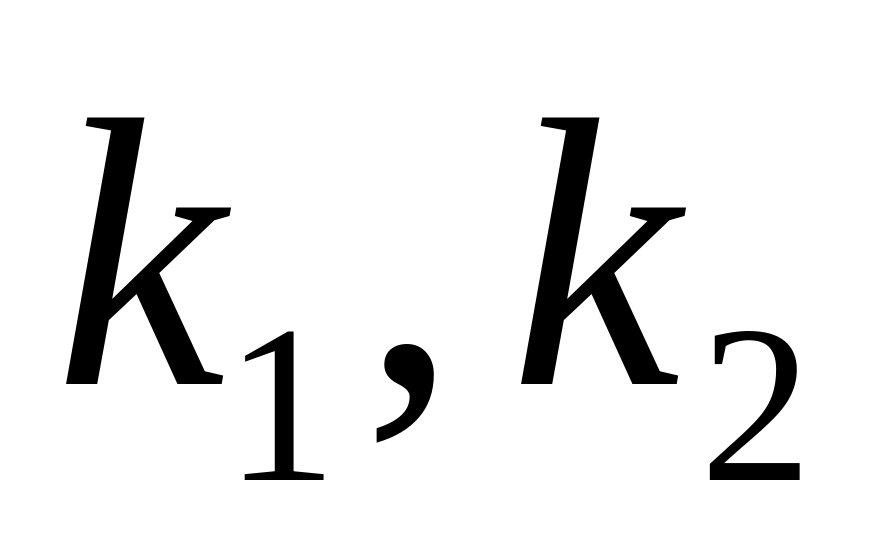причём
,
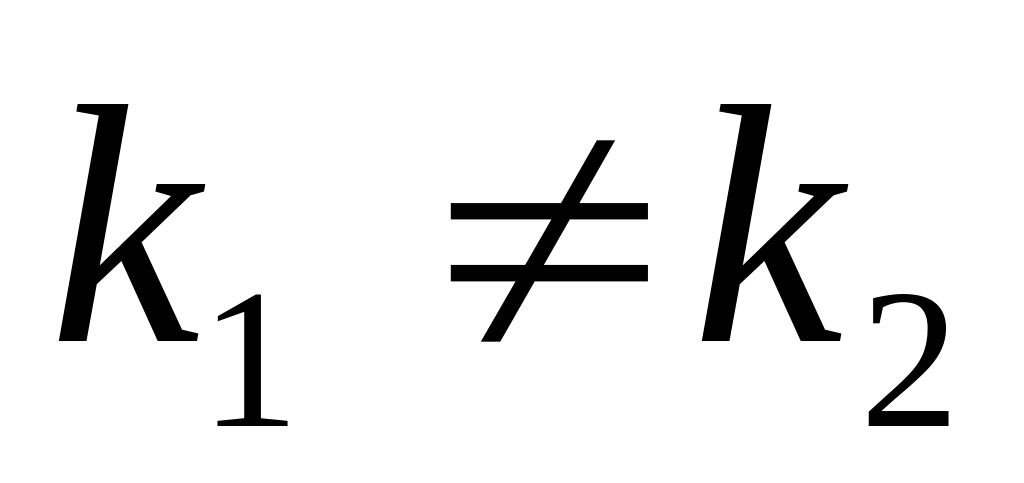и тогда, как доказано в теории,
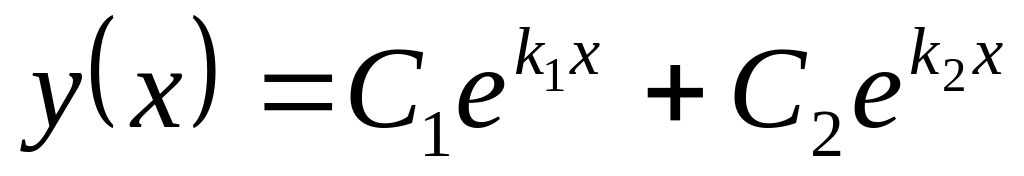;Если
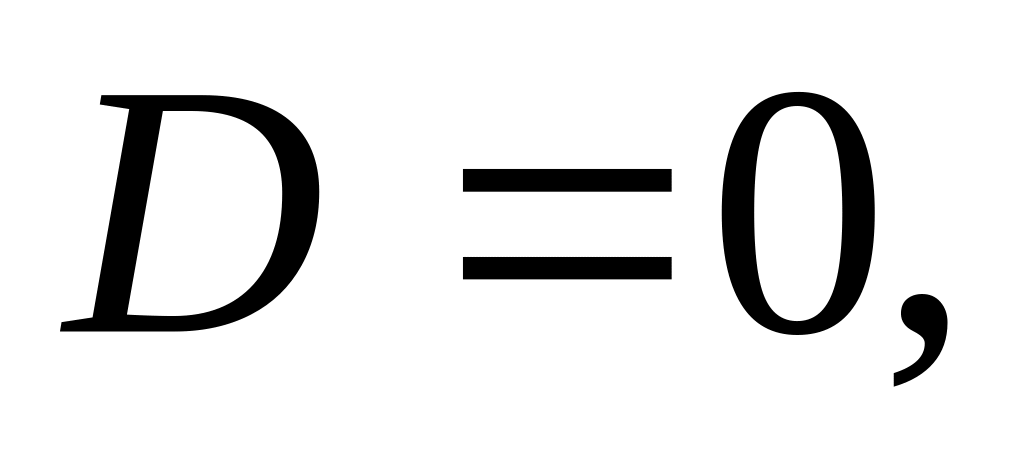уравнение имеет 2
одинаковых
корня
,
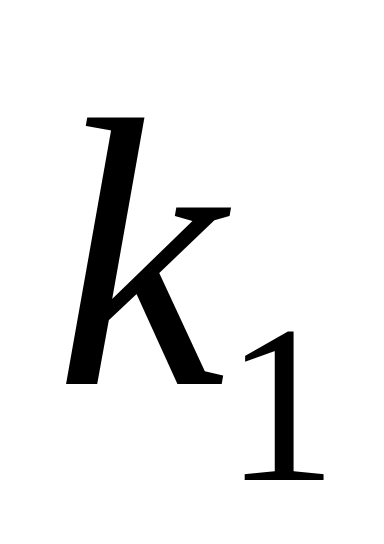поскольку
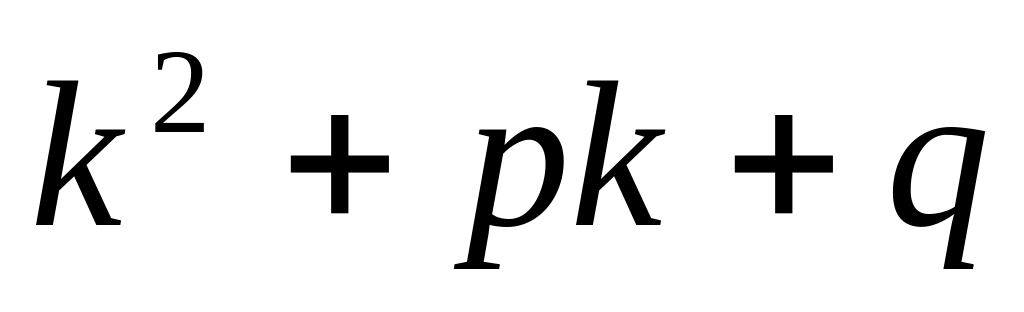2 раза
делится на
.
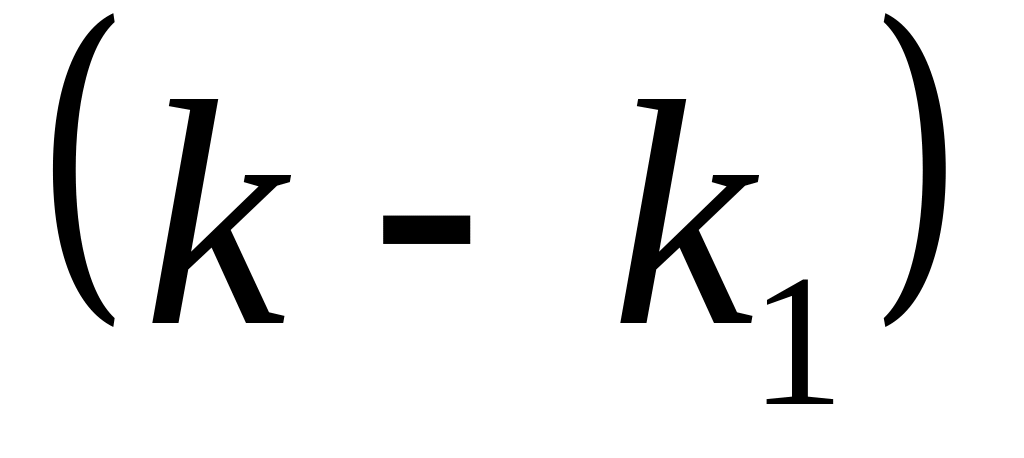В этом случае
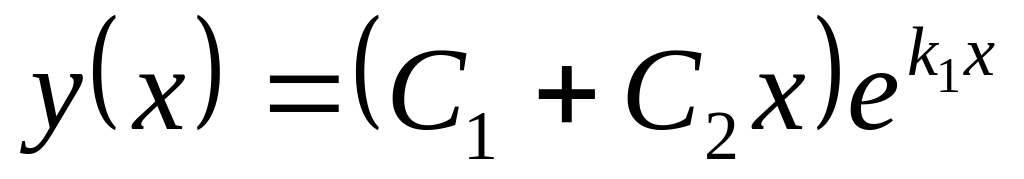;Если
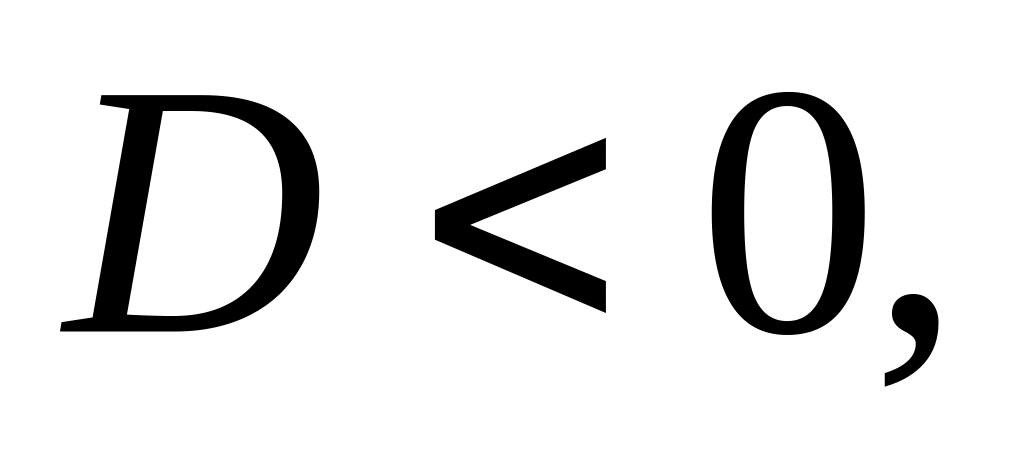уравнение имеет комплексные корни.
Находим параметры
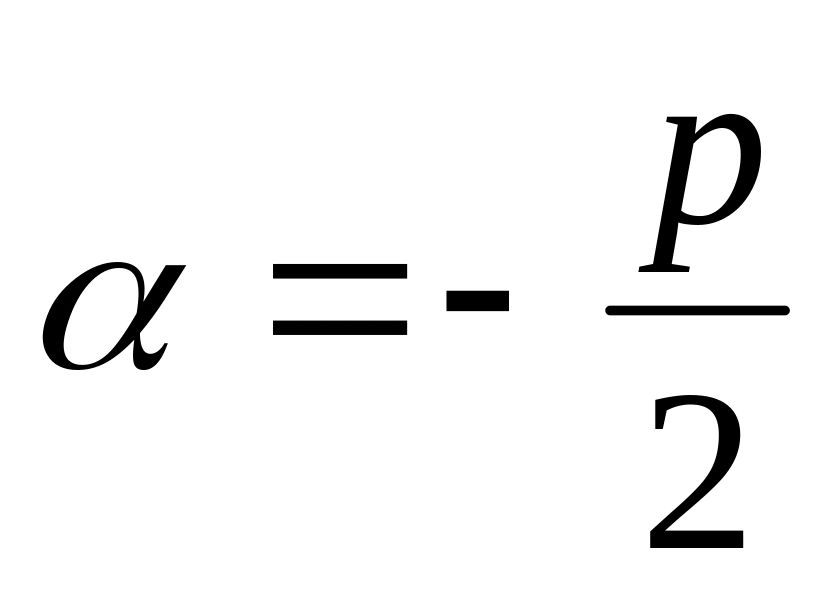и
,
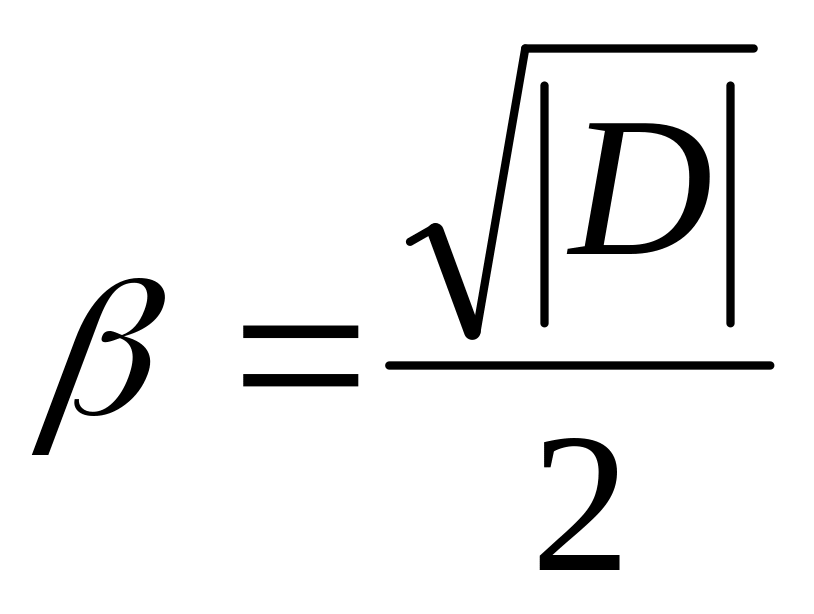тогда
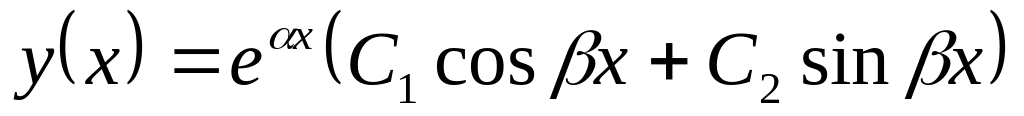.Для уравнения
,
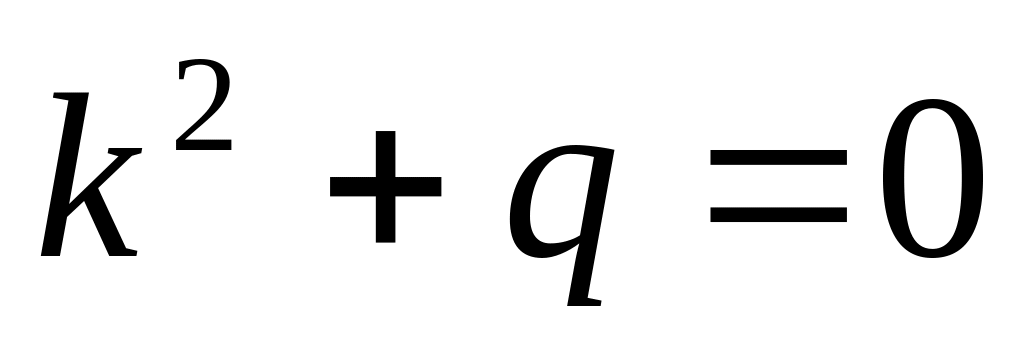где
,
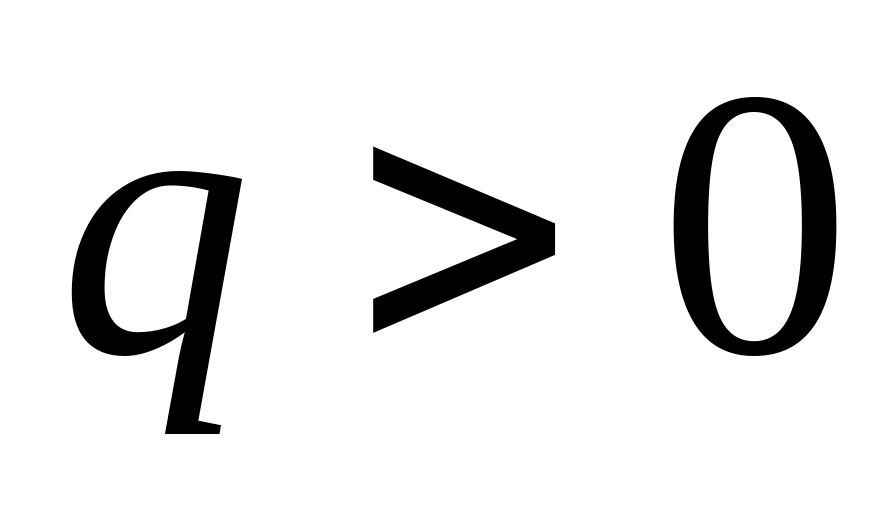в ситуации (4) получается
,
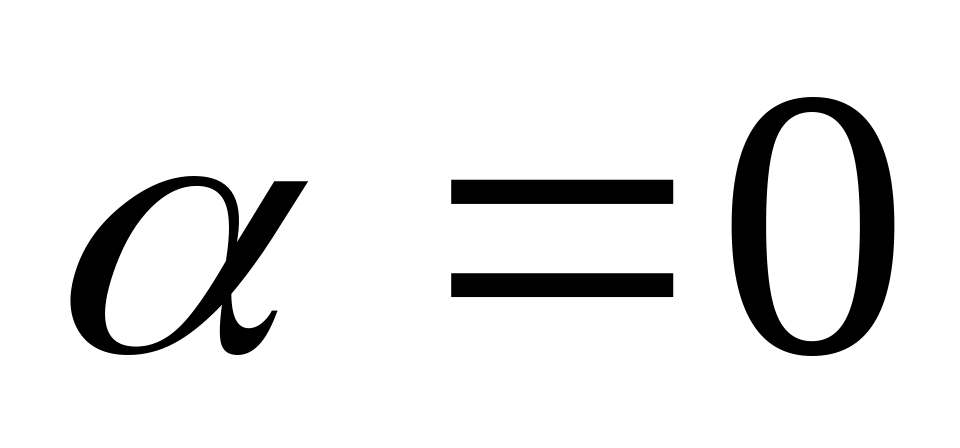и тогда
,
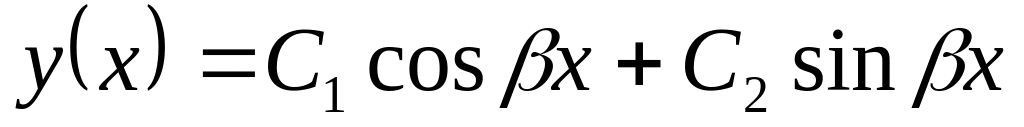где
.
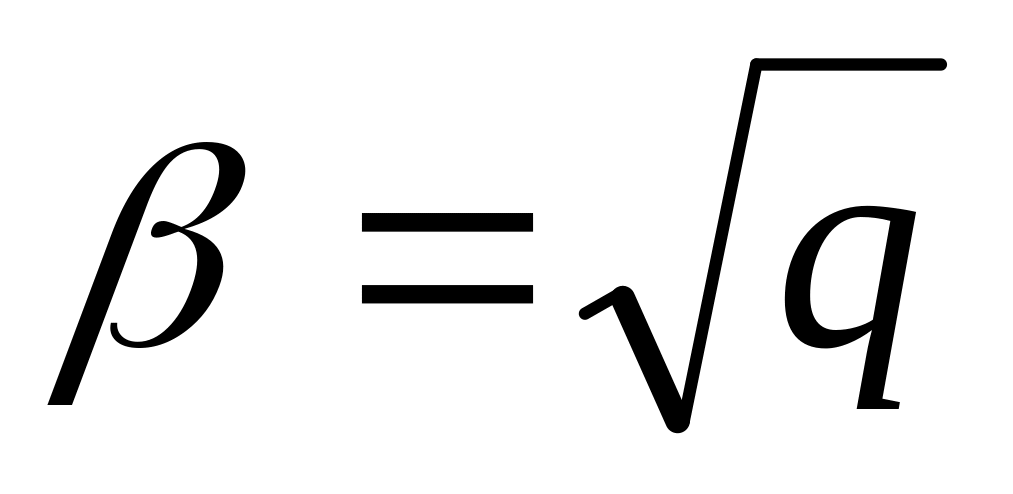Во всех случаях – произвольные постоянные, и – общее решение.
Удобно воспользоваться
обозначением мнимой
единицы
и считать, что при
получаем комплексно-сопряжённые
корни
.
Для уравнений
высокого порядка
получается характеристическое уравнение
,
каким-либо способом находятся все его
корни, решение составляется отдельно
для каждого корня, и все решения
суммируются. В экономике такие уравнения
возникают редко.
Пример 1.
Решим уравнение
.
Составляем характеристическое уравнение
,
его корни
действительны и не совпадают. Общее
решение
,
где
– произвольные постоянные.
Пример 2.
Для уравнения
соответствующее характеристическое
уравнение
имеет 2 совпадающих корня
.
Получаем общее решение
.
Пример 3.
Уравнение
приводит к характеристическому уравнению
,
или
.
Но
,
тогда
.
Пример 4.
Решая уравнение
,
из уравнения
получаем корни
.
В этом случае
.
В практических
задачах уравнение обычно дополняется
условиями
и
(или
и
),
и тогда можно найти значения констант
и получить частное
решение.
Пример 5.
Решим уравнение
при условии
.
Составляем уравнение
,
находим
,
составляем общее решение
.
Из условия
получаем уравнение
(поскольку
).
Чтобы учесть
условие
,
находим
и подставляем
и
:
.
Получили систему
,
из которой
и
.
Частное решение
,
или
.
Пример 6.
Решим уравнение
при начальном условии
.
Уравнение
имеет 2 корня
,
поэтому общее решение
.
Подставив
и
из условия
,
получаем, что
,
откуда
.
Затем находим
и подставляем
и
.
Приходим к системе
,
из которой
.
Частное решение
.
Пример 7.
Чтобы решить уравнение
с начальным условием
и
,
решаем уравнение
и по корням
составляем
общее решение
.
Чтобы найти , нам понадобится производная
.
Подставим
,
и
.
Поскольку
и
,
приходим к системе
Из неё следует,
что
и
,
и частное решение
,
или
.
ПК1.
Найдите общее решение уравнения
.
Найдите решение задачи Коши (частное
решение при указанных начальных
условиях):
1)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
2)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
3)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
4)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
5)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
6)
;
а) ; б) ; в) ;
г)
; д)
; е)
;
7)
;
а)
; б)
;
в)
; г)
;
д)
;
е)
.
ПК2. Найдите общее решение уравнения и частное решение, соответствующее краевому условию:
1) а)
; б)
; в)
;
г)
; д)
; е)
;
2) а)
; б)
; в)
;
г)
; д)
; е)
.
Пример 8.
Пусть дано уравнение
и условие
.
Составляем
уравнение
и по стандартной схеме получаем общее
решение
.
Подставим и :
;
Подставим
и
:
.
Частное решение
имеет вид
,
или
.
В общем случае приходится решать систему относительно .
Пример 9.
Решим уравнение
при условии
.
По характеристическому
уравнению
определяем, что
.
По условию, если , то , поэтому
;
Если же
,
то
,
и тогда
.
Умножив оба уравнения на 2, решаем алгебраическую систему
Можно выразить из
1-го уравнения
и подставить во 2-е, тогда
.
Значит,
.
Итак, частное
решение:
.
Неоднородное уравнение с постоянными коэффициентами
в общем случае решают методом вариации произвольных постоянных. При этом нередко получают интегралы, не берущиеся в элементарных функциях. Этот метод выходит за рамки пособия.
В простых случаях, когда правую часть уравнения можно представить в виде
,
где полиномы
,
а также числа a
и b
известны, применяют метод неопределённых
коэффициентов.
Его идея в том, что решение неоднородного уравнения можно представить как сумму двух решений:
– общего решения соответствующего однородного уравнения;
– частного решения неоднородного уравнения.
При этом частное
решение выглядит так же, как правая
часть, но отличается только коэффициентами
и, возможно, множителем
.
Идею метода и некоторые важные моменты лучше разобрать на примерах.
Пример 10.
Решим уравнение
,
где правая часть
а)
; б)
;
в)
;
г)
.
Решаем однородное
уравнение
.
Характеристическое уравнение
имеет два различных действительных
корня
и
,
и общее решение однородного
уравнения – функция
.
а)
правой части
соответствует частное решение
.
Когда правая часть
– полином, смотрим, был ли среди корней
0. Такого корня нет, поэтому
(иначе было бы
,
т.е.
).
Находим
и
.
Подставим их в левую часть уравнения:
.
Ищем
,
чтобы для всех x
выполнялось
.
Это равносильно тому, что
и
(коэффициенты при одинаковых степенях
переменной должны совпадать). Значит,
и
.
Итак, в случае а) частное решение
;
б)
по правой части
строим частное решение
.
Проверяем, было ли среди корней число
–2, стоящее перед переменной в показателе.
Такого корня нет, поэтому
без умножения на x.
Соответственно
;
.
Подставим в левую
часть уравнения:
.
Чтобы для всех x
выполнялось
,
достаточно равенства
,
или
.
Итак, в случае б) имеем
;
в)
когда справа
,
составляем
и смотрим, есть ли среди корней –5. Такой
корень есть:
,
поэтому умножаем на x:
.
Поиск производных немного усложняется:
;
.
Подставим:
.
Должно выполняться
,
поэтому
и
.
Получили, что
;
г)
по правой части
составим
.
Среди корней не было сопряжённой пары
,
и умножать
на переменную x
не надо.
Производные
;
подставляем в
уравнение
.
Получаем, что
или
.
Тогда
и
,
откуда
и
.
Значит,
.
Ответ:
,
где
а)
; б)
; в)
; г)
.
Пример 11.
Решим уравнение
,
где правая часть
а)
; б)
;
в)
;
г)
.
Однородное
уравнение имеет вид
.
Характеристическое для него – это
,
и его корни – числа
и
.
Общее решение однородного уравнения –
функция
,
или
.
а)
по правой части
составляем
и ищем число 0 среди корней характеристического
уравнения. Такой корень есть (
),
поэтому
.
Удобно раскрыть скобки:
.
Производные
и
подставим в уравнение
:
,
или
.
Приравниваем
коэффициенты при одинаковых степенях:
и
(справа отсутствует свободный коэффициент).
Очевидно,
,
тогда
.
Значит,
;
б)
когда справа
,
составляем
,
среди корней ищем число 2. Такого корня
нет, и умножать
на переменную x
не надо.
Находим
и
,
тогда
.
Но
,
поэтому
,
откуда
и
.
Итак,
;
в)
если
,
то
.
Но коэффициент –2 есть среди корней:
,
поэтому
.
Дифференцируем:
,
,
и подставляем в левую часть уравнения:
.
Из тождества
определяем, что
.
Тем самым
;
г)
для
составляем
и ищем среди корней сопряжённую пару
.
Такой пары нет, и
на
переменную x
не умножаем.
Дифференцируем:
,
,
Подставляем:
,
группируем:
,
приравниваем к
:
.
Система
имеет решение
и
.
Поэтому
.
Ответ:
,
где
а)
; б)
; в)
; г)
.
ПК 3. Найдите общее решение неоднородного уравнения.
1)
,
где
а)
; б)
; в)
;
г)
;
д)
;
е)
; ж)
; з)
;
2) , где
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
3)
,
где
а)
;
б)
; в)
;
г)
;
д)
.