§ 12. Линейные и однородные дифференциальные уравнения
Линейное
дифференциальное уравнение 1-го порядка
– это уравнение вида
,
где функции
известны. Предполагается, что решение
определено во всех точках, в которых
определены функции
и
.
Есть 2 основных способа решения таких
уравнений.
1-й способ.
Ищем решение в виде
или кратко,
.
Функцию
находим по собственному усмотрению, а
функцию
так, чтобы с учётом найденного
уравнение обратилось в тождество.
Для краткости
обозначим
и
.
Заметим, что
,
или
.
Тогда уравнение
превращается в
.
Подберём
так, чтобы выполнялось равенство
.
Разделив на v,
получаем уравнение с разделяющимися
переменными
.
Находим его решение – функцию u,
и подставляем в то, что осталось, а
именно, в уравнение
.
Находим v
и тем самым – общее решение
.
Функции
и
равноправны, поэтому можно вначале
решать уравнение
,
т.е.
,
а затем при полученном
– оставшееся уравнение
.
Результат получится тот же.
2-й способ.
Решаем соответствующее уравнение
.
Получаем некоторое
.
Но С
считаем не константой, а функцией
.
Производную от
подставляем в исходное
уравнение и получаем дифференциальное
уравнение относительно
.
Решив его, записываем окончательный
ответ.
Трудоёмкость способов примерно одинакова.
ЛО1. Найдите общее и частное решение линейного дифференциального уравнения. Сделайте проверку:
а)
; б)
; в)
;
г)
; д)
; е)
.
Пример 1.
Решим уравнение
в общем виде 1-м способом, затем найдём
частное решение для условия
.
Пусть
,
соответственно
.
Тогда
.
Подберём функцию u,
чтобы выполнялось
,
или
.
Поскольку
,
то
,
откуда
.
Из интеграла
находим, что
.
По свойствам логарифма
.
Подставив
в оставшуюся часть (в
),
получим, что
,
или
,
поэтому
.
Остаётся перемножить полученные u
и v.
Общее решение
уравнения – функция
,
или
.
Из условия
найдём C.
Подставим
и
в общее решение:
,
откуда
.
Функция
– частное решение.
Подставив
и
в исходное уравнение, проверим, выполнено
ли оно для всех x:
.
Получили тождество
.
Уравнение решено верно.
Ответ: общее решение , частное решение .
Пример 2.
Найдём 2-м способом общее решение
уравнения
,
а затем – частное решение для условия
.
Решаем уравнение
.
Оно равносильно уравнению
,
в котором можно разделить переменные:
,
затем
.
Интегрируем:
,
получаем
.
Удобно считать,
что
,
тогда по свойствам логарифма будет
,
откуда
(знак C
определится начальным условием).
Теперь считаем,
что
.
Найдём
и подставим вместе с решением y
в исходное уравнение:
.
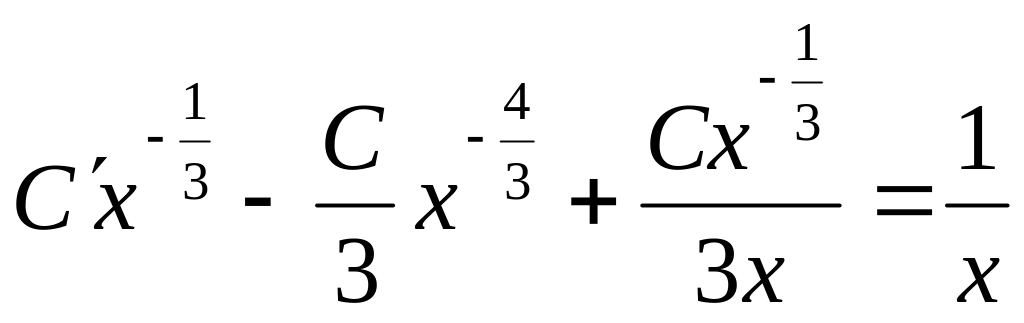Но
,
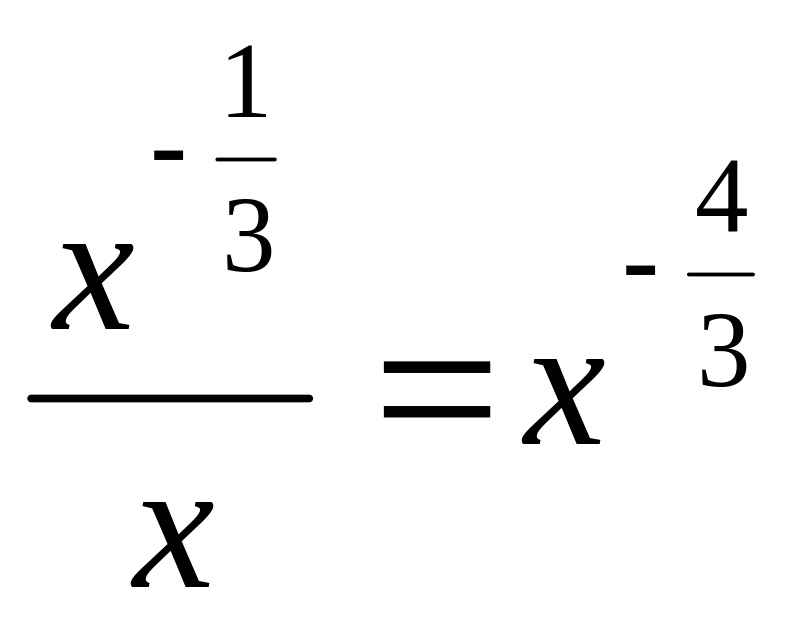и остаётся
,
что равносильно
,
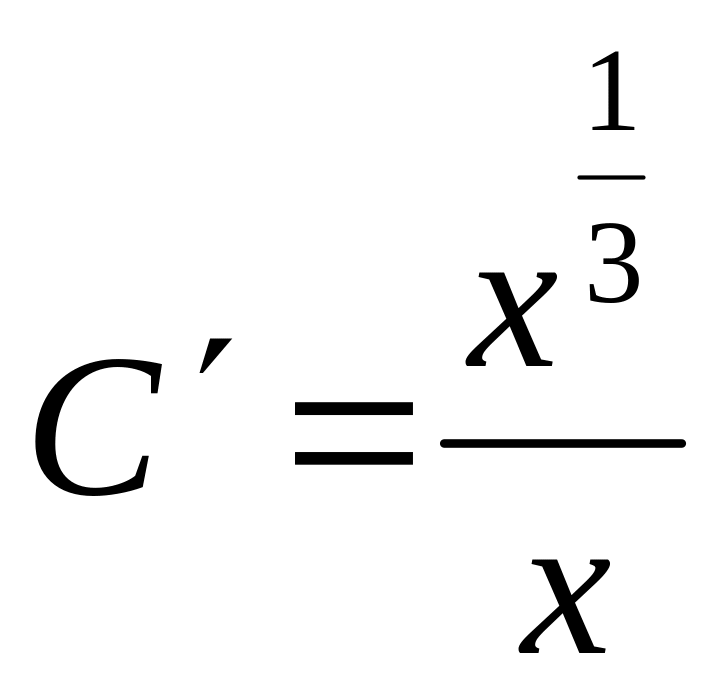или
.
Поэтому
,
где
уже
– обычная постоянная.
Таким образом,
,
т.е.
– общее решение уравнения.
Подставив в него
и
из начального условия
,
получаем, что
,
т.е.
и тем самым
.
Частное решение:
.
Подставим
и его производную
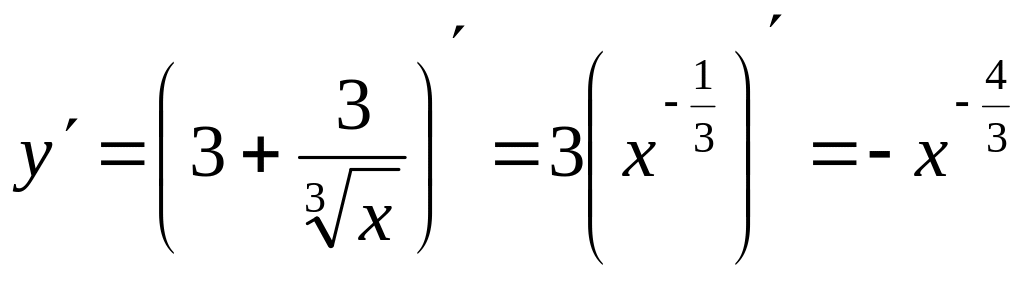в левую часть исходного уравнения:
.
Упростив, получаем
,
что совпадает с правой частью. Решение
верно.
Ответ: общее решение , частное решение .
ЛО2. Найдите общее и частное решение линейного дифференциального уравнения. Сделайте проверку:
а)
; б)
; в)
;
г)
; д)
; е)
.
Пример 3. Решим
1-м способом уравнение
.
Снова считаем,
что
и соответственно
,
тогда уравнение запишется как
,
или
.
Составляем систему
и решаем 1-е уравнение, сократив на v:
.
Подставим
во
2-е уравнение:
.
Тогда
.
Упростим:
.
Это – общее решение.
Чтобы найти
частное, подставляем в общее
и
,
согласно начальному условию. Получаем,
что
,
или
.
Тогда
.
Записываем частное решение
.
Проверим, что эта функция – решение задачи. Найдём производную
и подставим в левую
часть уравнения
:
.
Результат совпадает
с правой частью:
при любом x.
Также
,
что и должно быть по условию.
Ответ: общее решение , частное решение .
Уравнение
Бернулли имеет
вид
или приводится к такому. Здесь n
– любое конкретное число. Решается
уравнение теми же способами, что и
линейное, а заменой
и вовсе сводится к нему.
ЛО3. Найдите общее и частное решение уравнения Бернулли:
а)
; б)
; в)
;
г)
; д)
; е)
.
Пример 4.
Решим уравнение
с условием
.
Пусть
и
,
тогда
и
.
Составляем систему
и решаем 1-е уравнение, сократив на v:
.
Подставим
во 2-е уравнение:
,
откуда
.
Выразим функцию
:
и
.
Удобно обозначить
,
тогда
.
Общее решение
,
или
.
Подставив
и
,
найдём частное решение:
.
Ответ:
общее решение
,
частное –
.
Однородные
дифференциальные уравнения. Уравнение
называют однородным,
если для любого множителя t
(не обязательно числового) выполнено
равенство
.
Это означает, что фактически
– функция не от двух аргументов, а от
их отношения:
.
Однородные
уравнения можно сводить к разделяющимся
при помощи замены
,
где
– новая функция. При этом по свойствам
производной
.
Но
,
и тогда
,
где
.
Иногда однородное уравнение можно решить, как линейное, и наоборот – некоторые линейные уравнения решаются заменой .
Более того, несложное уравнение может оказаться и линейным, и однородным одновременно. Соответственно решить его можно любым способом.
Пример 5.
Заменим
и
,
тогда
,
или
.
Отсюда
.
В результате
,
где
.
Удобно заменить
,
тогда
.
Но
,
и получаем функцию
.
Тем самым
– общее решение уравнения.
При подстановке
в уравнение слева будет
,
а справа
.
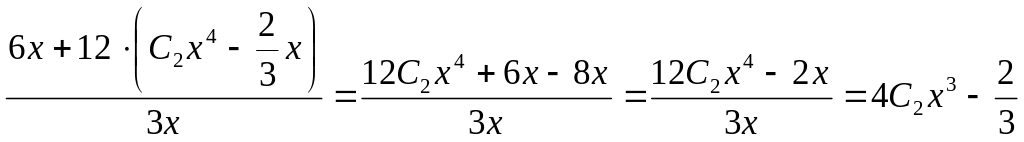При уравнение выполнено как тождество. Решение верно.
Ответ: .
ЛО4. Решите уравнение вначале как линейное (любым способом), затем как однородное. Найдите частное решение в каждом случае. Сравните результаты:
а)
; б)
;
в)
;
г)
; д)
;
е)
.
Пример 6.
Пусть дано уравнение
с условием
.
Решим его, считая линейным
(2-м способом):
.
Считая, что
,
находим
и подставляем в уравнение:
.
Записав как
,
получаем, что
,
или
.
Из условия
подставляем
,
откуда
и
.
Теперь решим
уравнение как однородное.
Делаем в исходном уравнении замену
и
:
,
откуда
и тем самым
,
где знак C
определяется начальным условием. Но
,
поэтому
,
что равносильно
.
Видно, что общие решения одинаковы, независимо от способа. Частные решения также совпадут.
Замечание. Если ответы выглядят по-разному, можно посмотреть, нельзя ли добиться совпадения при помощи каких-то свойств элементарной математики.
Например, решения
и
равносильны, поскольку
,
и слагаемые
поглощаются постоянной C.
При этом
и
– одно и то же обозначение
произвольной постоянной.
ЛО5. Решите уравнение 2 способами – как уравнение Бернулли и как однородное. Найдите частное решение в каждом случае:
а)
; б)
;
в)
.
Пример 7.
Решим двумя способами уравнение
.
1) Решение
однородного уравнения.
Заменяем
и
:
.
Разделяем переменные:
.
Таким образом,
.
Учтём, что
:
(в силу произвольного
знака C
считаем, что
).
Условие
означает, что
,
откуда
,
и тогда
.
Частное
решение:
,
или
.
Знак «–» невозможен по начальному
условию
.
Можно было выразить
,
где
переобозначено как C,
и подставить так:
,
и тоже исключить знак «–», при котором
нельзя получить
.
В любом случае
.
2) Решение
уравнения Бернулли.
Заменим
и
,
подставим:
.
Решим уравнение
,
или
:
.
Подставим
в оставшееся уравнение
:
,
и проинтегрируем:
.
Здесь величина
заменена постоянной C
в силу своей произвольности.
Таким образом,
– общее решение. Его можно записать в
виде
.
Поскольку при
должно быть
,
подставим:
.
Частное решение
совпадает с тем, что получено 1-м способом.
Совпадают и общие решения.
Ответ: – общее решение, – частное решение.
ЛО6. Решите однородное уравнение
а)
; б)
; в)
; г)
.
Пример 8. Пусть
.
Заменим
и
:
,
затем
.
Как обычно,
,
другой интеграл разобьем на 2:
.
Находим
а)
;
б)
,
тогда
.
Приравнивая
результат к
и умножая на –1, решение можно записать
так:
,
где
,
однако выразить или в явном виде невозможно.
ЛО7. Найдите общий интеграл однородного уравнения:
1) а)
; б)
; в)
;
2) а)
; б)
; в)
;
3) а)
; б)
; в)
.
Пример 9.
Пусть
.
По-прежнему
и
,
и
,
разделяем переменные:
,
по таблице находим
.
Это и есть общий интеграл уравнения.
Можно выразить :
.
Это уже – общее решение.
Задания 2) решаются так же, но применяется табличный интеграл
,
где
и
.
Например, уравнение
приводит к общему интегралу
,
откуда
.
Общее решение в явном виде существует, но выглядит громоздко.
При решении заданий 3) появится интеграл от квадратичного выражения, его можно найти заменой, как указано в § 3.