
Ермолаева Физика разделы Колебания и волны Оптика 2015
.pdfлизатора; α – угол между направлением колебаний света, падаю- щего на анализатор, и плоскостью пропускания анализатора (если колебания падающего света совпадают с этой плоскостью, то ана- лизатор пропускает длинный свет без ослабления).
Степень поляризации света равна
P = |
Imax − Imin |
, |
(1.84) |
|
Imax + Imin |
||||
|
|
|
где Imax и Imin – максимальная и минимальная интенсивности ча- стично поляризованного света, пропускаемого анализатором.
Угол поворота плоскости поляризации φ монохроматического света при прохождении через оптически активное вещество равен:
а) в твердых телах
ϕ = αd, |
(1.85) |
где α – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
б) в растворах
φ = [α]Cd , |
(1.86) |
где [α] – удельное вращение; C – массовая |
концентрация опти- |
чески активного вещества в растворе; |
|
в) в чистых жидкостях |
|
φ = [α]ρd, |
(1.87) |
где ρ – плотность жидкости. |
|
1.1.8. Законы теплового излучения
Закон Стефана–Больцмана |
|
|
|
R |
= σT 4 |
, |
(1.88) |
e |
|
|
|
где Re – излучательность (энергетическая светимость) абсолютно черного тела; σ – постоянная Стефана–Больцмана; Т – термо- динамическая температура.
Закон смещения Вина
λ0 = b / T , |
(1.89) |
где λ0 – длина волны, на которую приходится максимум энергии излучения; b – постоянная Вина (b = 2,90∙10-3 мК).
Формула Планка
21
r |
= |
2πhc2 |
|
1 |
|
, |
(1.90) |
|||
|
λ5 |
exp(hc / λkT ) −1 |
||||||||
λ,T |
|
|
|
|
||||||
rω,T = |
ω3 |
|
|
1 |
|
, |
(1.91) |
|||
4π2с2 |
|
|
exp( ω / kT ) −1 |
|||||||
где rλ,T , rω,T – спектральные плотности энергетической светимости абсолютно черного тела; h – постоянная Планка; – штрихованная постоянная Планка; λ – длина волны; ω – круговая частота; с – ско- рость света в вакууме; Т – термодинамическая температура; k – постоянная Больцмана.
1.1.9. Фотоэффект. Давление света |
|
|||||
Энергия фотона равна |
|
|
|
|
|
|
ε = hν |
или ε = ω , |
(1.92) |
||||
где h – постоянная Планка; |
– штрихованная постоянная Планка; |
|||||
ν – частота фотона; ω – циклическая частота. |
|
|||||
Масса фотона определяется по формуле |
|
|||||
m = |
ε |
= |
h |
, |
(1.93) |
|
c2 |
|
|||||
|
|
|
cλ |
|
||
где с – скорость света в вакууме; λ – длина волны фотона. |
|
|||||
Импульс фотона равен |
|
|
|
|
|
|
p = mc = h / λ. |
(1.94) |
|||||
Формула Эйнштейна для фотоэффекта имеет вид
hν = A |
+ Т |
|
= A + |
mV2 |
|
|
mаx |
max |
, |
(1.95) |
|||
|
||||||
вых |
|
вых |
2 |
|
|
|
|
|
|
|
|
|
|
где hν – энергия фотона, падающего на поверхность металла; Авых – работа выхода электрона с поверхности металла; Tmax – максималь- ная кинетическая энергия фотоэлектронов.
Красная граница фотоэффекта определяется по формуле
ν0 = Aвых / h , λ0 = hc / Aвых , |
(1.96) |
где ν0 – минимальная частота света, при которой еще возможен фо- тоэффект; λ0 – максимальная длина волны света, при которой еще возможен фотоэффект.
22
Давление света при нормальном падении на поверхность определяется по формуле
p = |
Ee |
(1+ ρ) = ω(1+ ρ) , |
(1.97) |
|
|||
|
c |
|
|
где Ее – облученность поверхности; ω – объемная плотность энер- гии излучения; ρ – коэффициент отражения света поверхностью.
1.1.10. Эффект Комптона. Атом водорода по теории Бора
Формула Комптона имеет вид
Δλ = λ′ − λ = |
h |
(1 − cos θ) |
или Δλ = λ′ − λ = 2 |
h |
2 θ |
|
(1.98) |
|
|
|
sin |
2 |
, |
||||
m c |
m c |
|||||||
0 |
|
0 |
|
|
|
|
||
где λ – длина волны фотона, встретившегося со свободным или слабо связанным электроном; λ′ – длина волны фотона, рассеян- ного на угол θ после столкновения с электроном; m0 – масса по- коящегося электрона.
Комптоновская длина волны определяется по формуле
λC = |
h |
. |
(1.99) |
|
|
||||
m c |
||||
|
|
|
||
|
0 |
|
|
При рассеянии фотона на электроне λC = 2,436 пм.
Первый постулат Бора (постулат стационарных состояний): в
атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии.
В стационарном состоянии атома электрон, двигаясь по круго- вой орбите, имеет дискретные квантованные значения момента им- пульса, удовлетворяющие условию
meVrn = n (n = 1, 2,3,...), |
(1.100) |
где me – масса электрона, V – его скорость по n-й орбите радиуса
rn.
Второй постулат Бора (правило частот): при переходе элек-
трона с одной стационарной орбиты на другую излучается (погло- щается) один фотон с энергией равной разности энергий соответ- ствующих стационарных состояний:
hν = En − Em , |
(1.101) |
23
где En и Em – соответственно энергии стационарных состояний ато- ма до и после излучения (поглощения).
При En < Em происходит излучение фотона (переход атома из со- стояния с большей энергией в состояние с меньшей энергией, т.е. переход электрона с более удаленной от ядра орбиты на близлежа- щую), при En > Em – его поглощение (переход атома в состояние с большей энергией, т.е. переход электрона на более удаленную от ядра орбиту).
Выражение для радиуса n-й стационарной орбиты:
|
r = n2 |
2 4πε |
0 |
(п = 1,2,3,…). |
(1.102) |
|||||||||
|
m Ze2 |
|||||||||||||
|
n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
Для атома водорода (Z = 1) радиус первой орбиты электрона при |
||||||||||||||
n = 1, называемый первым боровским радиусом (а), равен |
|
|||||||||||||
r |
= a = |
2 4πε |
0 |
= 0,528 10−10 м = 52,8 пм . |
(1.103) |
|||||||||
m e2 |
|
|||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
Собственные значения энергии Еn электрона в атоме водорода |
||||||||||||||
|
|
E |
|
= − |
|
|
me4 |
|
|
1 |
, |
1.104) |
||
|
|
n |
32π2ε 2 |
2 n2 |
||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
где ћ – перечеркнутая постоянная Планка; n – главное квантовое число (n = 1, 2, 3…).
Самый нижний уровень Е1, отвечающий минимальной возмож- ной энергии, – основной, все остальные (En > E1, n = 1, 2, 3, …) –
возбужденные.
При E < 0 движение электрона является связанным, а при E > 0
– свободным. Область непрерывного спектра Е > 0 соответствует
ионизированному атому.
Частота спектральной линии, излучаемой атомом водорода при квантовом переходе с уровня En2 на уровень Еn1,
|
|
|
me4 |
|
|
|
|
1 |
|
1 |
|
|
||||
hν = En2 |
− En1 = |
|
|
|
|
|
|
|
|
|
|
− |
|
|
. |
(1.105) |
|
2 |
ε |
|
2 |
2 |
n |
2 |
n |
2 |
|||||||
|
|
32π |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|||||
Обобщенная формула Бальмера: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ν = R |
1 |
− |
1 |
|
, |
|
|
|
|
|
|
(1.106) |
|||
|
2 |
2 |
|
|
|
|
|
|
|
|||||||
|
|
m |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
24
где R = 3,293 1015 с-1 – постоянная Ридберга, m и n – целые числа,
причем для данной серии n = m + 1, m + 2, m + 3 и т.д.
Всего различают шесть серий спектральных линий: серия Лай- мана (m = 1), серия Бальмера (m = 2), серия Пашена (m = 3), серия Брэкета (m = 4), серия Пфунда (m = 5), серия Хэмфри (m = 6).
Спектральная формула для длин волн линий в спектре водорода
1 |
= R′ |
1 |
− |
1 |
, |
(1.107) |
λ |
2 |
2 |
||||
|
n |
|
n |
|
|
|
|
1 |
2 |
|
|||
где R′ = 1,1 107 м-1 – постоянная Ридберга.
1.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.1. Материальная точка совершает гармонические ко- лебания с частотой ν = 0,5 Гц. Амплитуда колебаний А = 10 см. Определить скорость точки в момент времени, когда смещение
х = 6 см.
Дано: |
|
СИ |
|
|
|
Решение. |
|
||
|
|
|
|
|
|||||
|
|
|
|
1. |
Уравнение гармонических коле- |
||||
ν = 0,5 Гц |
|
|
|
|
|
||||
|
0,01 м |
|
баний имеет вид: |
|
|||||
А = 10 см |
|
|
|
||||||
|
|
|
|
|
|
x = Acos(ωt + ϕ), |
(1) |
||
х = 6 см |
|
0,06 м |
|
|
|
|
|
||
|
|
где ϕ – начальная фаза. |
|
||||||
υ = ? |
|
|
|
|
|||||
|
|
|
|
|
|
Мгновенная скорость материальной |
|||
точки, совершающей гармонические колебания, равна |
|
||||||||
|
|
|
υ = − Aωsin(ωt + ϕ). |
(2) |
|||||
Исключим из (1) и (2) время t, возведя оба уравнения в квадрат: |
|||||||||
|
|
x2 = A2 cos2 (ωt + ϕ), |
(3) |
||||||
|
|
υ2 = A2ω2 sin2 (ωt + ϕ). |
(4) |
||||||
Разделим уравнение (3) на |
А2, уравнение (4) на А2ω2 |
и сложим |
|||||||
полученные выражения: |
|
х2 |
|
υ2 |
|
|
|||
|
|
|
|
+ |
= 1 . |
(5) |
|||
|
|
|
|
А2 |
А2ω2 |
||||
|
|
|
|
|
|
|
|||
Выразим из (5) скорость: |
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
υ2 = 1 |
− |
х |
|
А2ω2 = (А2 − х2 ) ω2 |
|
||
|
|
2 |
|
||||||
|
|
|
|
А |
|
|
|
|
|
25

υ = ω А2 − х2 . |
(6) |
С учетом того, что ω = 2πν, получим:
υ = 2πν А2 − х2 . |
(7) |
Подставим в (7) числовые значения в системе СИ:
υ = 2 3,14 0,5 0,12 − 0,062 = 0, 25 м / c.
Ответ: υ = 0,25 м/с.
Задача 1.2. Полная энергия тела, совершающего гармонические колебания равна Е = 24 мкДж, максимальная сила, действующая на тело Fmax = 2,0 мН. Написать уравнение движения того тела, если период колебаний Т = 2 с и начальная фаза φ = π/6.
Дано: |
|
СИ |
|
|
Решение. |
|
|
|||
|
|
|
|
|
||||||
|
|
|
1. Полная энергия тела, |
со- |
||||||
Е = 24 мкДж |
|
24 10-6 Дж |
|
|
||||||
Fmax = 2,0 мН |
|
2 10-3 Н |
|
вершающего гармонические |
ко- |
|||||
Т = 2 с |
|
|
|
лебания: |
|
|
||||
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
||||
φ = π/6 |
|
|
|
|
|
E = |
|
mA2 |
ω2 , |
(1) |
|
2 |
|||||||||
x = f(t) = ? |
|
|
|
где m, А – масса точки и амплиту- |
||||||
|
|
|
|
|||||||
да ее колебаний; ω – круговая (циклическая) частота: |
|
|
||||||||
|
|
|
ω = |
2π |
. |
|
(2) |
|||
|
|
|
|
|
||||||
|
|
|
|
|
Т |
|
|
|||
2. Согласно второму закону Ньютона сила равна F = ma, откуда максимальная сила:
F max = mamax .
3. Ускорение тела, совершающего гармонические определяется по формуле
a = −Aω2 cos(ωt + ϕ) = −a |
|
cos(ωt |
+ ϕ) , |
||||||
|
|
|
|
max |
|
|
|
|
|
следовательно, |
|
|
2π 2 |
|
|
|
|
|
|
2 |
|
|
= |
4π2 A |
|
||||
amax = Аω |
= |
A |
|
|
|
|
, |
||
|
T |
2 |
|||||||
|
|
|
T |
|
|
|
|
||
(3)
колебания,
(4)
(5)
4. |
С учетом (5) получим |
4π2тА |
|
|
|
2 |
|
|
|
|
F = mAω = |
|
, |
(6) |
|
Т2 |
|||
|
тах |
|
|
|
5. |
Выразим амплитуду колебаний А из уравнений (1) и (6): |
|
||
26

|
|
Е |
1 |
|
|
|
А |
|
|
|||||
|
|
|
|
= |
|
mA2ω2 : mAω2 = |
|
|
, |
|
|
|||
|
|
F |
2 |
2 |
|
|
||||||||
|
|
|
тах |
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
24 10−6 |
|
|
|
|
|
|
|
|||||
А = 2 |
Е |
= 2 |
= 24 10−3 м = 0,024 м. |
|
||||||||||
|
2 10−3 |
|
||||||||||||
|
F |
|
|
|
|
|
|
|
|
|||||
|
max |
|
|
|
|
|
|
|
|
|
|
|
||
6. Общее уравнение гармонических колебаний: |
|
|
||||||||||||
|
x = Asin(ωt + ϕ) = Asin |
2π |
t + ϕ |
. |
(7) |
|||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
||||
7.Подставим в (7) числовые значения:
x= 0,024sin 22π t + π6 = 0,024sin πt + π6 .
Ответ: x = 0,024sin |
πt + |
π . |
|
|
6 |
Задача 1.3. Разность потенциалов на обкладках конденсатора в колебательном контуре изменяется со временем по закону U = = 100sin1000πt. Электроемкость конденсатора 0,5 мкФ. Определить период собственных колебаний, индуктивность, энергию контура и максимальную силу тока, текущего по катушке индуктивности.
Дано: |
|
СИ |
|
Решение. |
|
|
|
|
|
||||
|
|
1. Напряжение на |
об- |
|||
U = 100sin1000πt |
|
|
|
|||
|
-6 |
|
кладках |
конденсатора |
ме- |
|
С= 0, 5 мкФ |
|
Ф |
||||
|
0,5 10 |
няется |
по гармоническому |
|||
Т = ? L = ? W = ? Imax =? |
|
|
|
|||
|
|
|
закону |
|
|
|
|
|
|
|
|
|
|
(1)
– максимальное значение напряжения на обкладках кон- денсатора, w – собственная циклическая частота колебаний, кото- рая связана с периодом соотношением
T = |
2π |
. |
(2) |
|
|||
|
w0 |
|
|
По условию задачи, U = 100sin1000πt, таким образом, имеем
Umax = 100 В, w = 1000π с-1, тогда
T = |
2π |
= |
2π |
= 0,002 с . |
|
1000π |
|||
|
w |
|
||
0 |
|
|
|
|
27
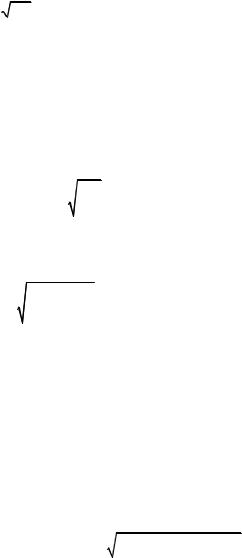
2. Период собственных колебаний в контуре определяется по
формуле Томсона T = |
2π |
|
LC , отсюда |
|
||||
L = |
T |
2 |
|
= |
|
0,0022 |
= 0, 2 Гн. |
(3) |
4π2C |
|
4 3,142 0,5 10−6 |
||||||
3. Энергия контура равна максимальной энергии поля конденса- тора Wэ max или максимальной энергии катушки индуктивности
Wм max: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = W |
|
= W |
|
= |
|
CU max2 |
= |
LImax2 |
, |
(4) |
||||
|
|
|
|
|
|
|
|||||||||
|
эmax |
|
|
мmax |
2 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
= |
|
2W |
. |
|
|
|
(5) |
||
|
|
|
max |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
0,5 10−6 |
1002 |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
= 2,5 10−3 Дж = 2,5 мДж, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2,5 10−3 |
|
|
|
|
|||||||
|
Imax = |
|
|
|
|
|
|
|
= 0,15 А. |
|
|
||||
|
|
|
0, 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: Т = 2 мс, L = 0,2 Гн, W = 2,5 мДж, Imax = 0,15А.
Задача 1.4. В цепь, состоящую из последовательно соединен- ных резистора сопротивлением R = 20 Ом, катушки индуктивности L = 36 мГн и конденсатора емкостью С = 28 мкФ подключено внешнее переменное напряжение с амплитудным значением Umax = = 180 В и частотой ω = 314 рад/с. Определить амплитудное значе- ние силы тока Imax в цепи и сдвиг фаз ϕ между током и внешним напряжением.
Дано: |
|
СИ |
|
Решение. |
|
|
|
|
|
||||
|
|
1. Полное сопротивление це- |
||||
R = 20 Ом |
|
|
|
|||
|
36 10-3 Гн |
|
пи равно |
|
||
L = 36 мГн |
|
|
|
|||
С = 28 мкФ |
|
28 10-6 Ф |
|
Z = |
R2 + (ωL −1/ (ωC))2 . |
(1) |
ω = 314 рад/с |
|
|
|
2. |
Связь между током |
и |
Umax =180 В |
|
|
|
|||
|
|
|
напряжением |
|
||
Imax = ? ϕ = ? |
|
|
|
(2) |
||
|
|
|
|
Umax = ImaxZ, |
||
|
|
|
|
|||
28

Откуда
I |
|
= |
Um |
= |
Um |
. |
(3) |
m |
|
R2 + (ωL −1 / (ωC))2 |
|||||
|
|
Z |
|
|
|||
|
|
|
|
|
|||
3. Сдвиг фаз между током и внешним напряжением определим из формулы
tg ϕ = ωL −1/ (ωC) ,
|
|
R |
|
откуда |
|
|
|
|
ϕ = arctg ωL −1/ (ωC) . |
||
|
|
R |
|
4. Подставим в (3) и (5) числовые значения: |
|||
Imax = |
180 |
|
=1,72A, |
|
|
||
202 + (314 36 10−3 −1/ |
|
||
|
(314 28 10−6 ))2 |
||
ϕ = arctg 314 36 10−3 −1 / (314 28 10−6 ) =
20
= arctg(−5,122) = −78,95°
Знак минус указывает на то, что ток опережает напряжение.
Ответ: Imax = 1,72 А, ϕ = –78,95°.
(4)
(5)
Задача 1.5. Энергия затухающих колебаний маятника, происхо- дящих в некоторой среде, за время t = 2 мин, уменьшилась в N = = 100 раз. Определить коэффициент сопротивления, если масса маятника m = 0,1 кг.
Дано: |
|
СИ |
|
Решение. |
|
|
|
|
|
||||
|
|
1. Коэффициент сопротивления r |
||||
t = 2 мин |
|
120 |
с |
|
||
|
|
связан с коэффициентов затухания β |
||||
N = 100 |
|
|
|
|
||
|
|
|
|
и массой тела m соотношением |
|
|
m = 0,1 кг |
|
|
|
|
|
|
|
|
|
|
r = 2mβ. |
(1) |
|
r = ? |
|
|
|
|
||
|
|
|
|
2. Полная энергия тела, соверша- |
||
|
|
|
|
|
||
ющего гармонические колебания, определяется формулой |
|
|||||
29

W = |
mw2 A2 |
. |
(2) |
|
|||
2 |
|
|
|
3. Обозначим начальное и конечное значение энергии колебаний через W0 и W соответственно и найдем отношение данных величин c учетом исходных данных:
W0/W = (A0/A)2 = N, |
(3) |
откуда
A0 = N . A
Для затухающих колебаний справедливо соотношение
|
|
|
|
|
А |
= А е−βt , |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
ln ( N ) |
|
|
|||
|
|
|
|
|
ln |
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
β = |
|
|
A |
= |
|
|
|
. |
|
|||
|
|
|
|
t |
|
|
|
t |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
C учетом (6) из выражения (1) получаем |
|
|
|||||||||||||
r = |
2m |
ln ( |
N ) |
= 2 |
0,1 |
ln ( |
100 ) |
|
= 0,0038 |
кг/с |
|||||
|
|
|
|
|
|
|
|||||||||
|
t |
120 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: r = 0, 0038 кг/с.
(4)
(5)
(6)
Задача 1.6. Груз массой m = 300 г, подвешенный на спиральной пружине жесткостью k = 30 Н/м, совершает колебания в вязкой среде с коэффициентом сопротивления r = 0,6 кг/с. На верхний ко- нец пружины действует вынуждающая сила, изменяющаяся по за- кону F = 0,2sinωt Н. Определить коэффициент затухания β данной колебательной системы и резонансную амплитуду Арез.
Дано: m = 300 г
k =30 Н/м r = 0,6 кг/с
F = 0,2sinωt Н
β = ? Арез = ?
СИ |
|
Решение. |
β |
|
|
||||
|
1. Коэффициент затухания |
|||
0,3 |
кг |
|
||
|
системы определим из соотноше- |
|||
|
|
|
||
|
|
|
ния |
|
|
|
|
β = r/2m, |
(1) |
|
|
|
где r – коэффициент сопротивле- |
|
|
|
|
ния; m – масса тела. Тогда |
|
|
|
|
|
|
β = 0,6/2 0,3 = 1 с-1. |
|
|||
30
