Катин МОЛЕЦУЛАР ДЫНАМИЦС ИН МУЛТИСЦАЛЕ МОДЕЛИНГ 2015

A.Write the interatomic distance every twenty steps (every 20 fs) and compute the average value. Define how many values should be averaged to reach the convergence. The convergence criterion implies that the doubling the number of values does not lead to the changing of the average.

B.Vary the v to define the dependence of the averaged molecule

length l on the microcanonical temperature Tm. Make the linear approximation of the l(Tm) dependence and derive the “linear expansion coefficient” for the hydrogen molecule.

Monte-Carlo methods as an alternative to MD

MD simulation is not the only way to obtain the thermodynamically correct sampling of the system’s states. The deserved alternative is the Monte-Carlo methods that generate the sequence of states using the special algorithms based on the random numbers. Note that the MonteCarlo methods are applicable only to equilibrium processes. MD and Monte-Carlo methods usually demonstrate nearly the same computational efficiencies in the study of system’s phase space. But in some cases one of these approaches will be more preferable.

The Metropolis algorithm

The Metropolis algorithm is very simple and especially computationally efficient method that provides generation of the statistically correct sampling of the states for the case of canonical ensemble. In the frame of the algorithm, a new state is chosen randomly (for example, all nuclei positions are randomly changed). If the potential energy U of a new state is lower than the energy of the current one, a new state is certainly accepted and added in the sampling, and further regarded as the current. Otherwise, a new state is accepted with the exp(– U/T) probability or rejected (with the 1 – exp(– U/T) probability), where U is the energy difference between the new and the current states and T is the temperature. In the case of rejection, the current state is further regarded as current one. Also, it is added to the sampling once again.

To clarify the idea of the algorithm, let us consider the simplest model system, which can be located only in two states: ground and exited. Energies of these states are equal to Ug = 0 and Ue = 100 meV, re-

31

spectively. The system is in thermal contact with the thermostat, and thermostat has the temperature T = 50 meV (canonical ensemble). With regard to these assumptions, the ground state is more energetically favorable. The probability to find the system in this state is equal to

The probability to find the system in the exited state is equal to 0.12 that is ≈ 7 times less than 0.88. So, the averaged energy of the system can be calculated as 0.88Ug + 0.12Ue = 12 meV. Correct statistical sampling should include approximately seven ground states per each exited state.

Let us apply the Metropolis algorithm to this system. If the exited state is current, then new state is ground and it is certainly accepted. If the ground state is current, the next state is exited and it can be accepted with the probability exp(–(Ue – Ug)/T) ≈ 1/7. Therefore, in the average the only seventh attempt to conversion to the exited state will be successful. So, the sampling obtained within the Metropolis algorithm contains seven ground states per one exited state as it is required. Complex systems have many billions of states. However, the Metropolis algorithm allows choosing a few thousands of them to reproduce the system properties correctly.

Exercise 32. Let us consider the system that has only three states: one ground and two exited. Their potential energies are Ug = 0, Ue1 = 20 meV, Ue2 = 50 meV. The temperature is equal to 300 K.

A.Calculate the mean potential energy of the system.

B.Let us consider that the system is investigated using the Metropolis algorithm. Obtain the probabilities of the following transitions: g

→e1, g → e2, e1 → e2, e1 → g, e2 → e1, e2 → g.

Criterion of the event appearing

If the non-equilibrium problem is solved, then the Metropolis algorithm is inapplicable. In this case, the MD simulation is running until the specific event will be occurred. Multiplying the time step value by the number of steps passed, one can obtain the full time required for the process. So, it is important to identify the appearance of the expected event during the MD simulation.

If the chemical reaction plays the role of the event, then the most re-

32

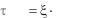
liable criterion is to optimize geometry of the system and find its potential energy. Changing in the potential energy indicates that the reaction was passed. In many cases, the simple geometry criteria based on the interatomic distances are used. It is considered that the covalent bond is formed if the interatomic distance becomes smaller than ≈ 1.8 Å. On the other hand, larger interatomic distances indicate the bond rupture. For the study of phase transition, the monitoring of the order parameter at every MD step is needed. The changing of microcanonical temperature (for the isolated molecule) can also imply that the chemical reaction or phase transition are finished. Sometimes the visual analysis of the calculated data as a molecule animation is very effective.

Thermal decay as an example of non-equilibrium process

Thermal decay is one of the simplest examples of chemical reaction that characterized by the decomposition of the molecule into a few parts under the influence of its thermal oscillations. MD simulation can provide the observation of this process in a “real-time mode”. Therefore, it helps to identify the decay channels, intermediate and final products. MD simulation provides the detailed understanding of physical and chemical processes concerned with the reaction. The determination of the reaction trajectory opens wide possibilities for the design of its optimization. The molecule lifetime τ can be also defined. Note that the τ value depends on the initial nuclei positions and velocities. Nevertheless, we can compute the averaged value of τ, which is defined by the system’s temperature. To compute the averaged value, one should repeat the same MD simulation of thermal decay for different initial conditions chosen randomly.

Let us consider the thermalized system at the temperature T. Its average lifetime can be calculated by using the Arrhenius law:

where Ea is the activation energy that can be interpreted as the minimum potential energy required for decomposition, and ξ is the reverse frequency factor, which is equal to the average lifetime at the “infinity” temperature. Note that the decay is possible even at very low temperatures, due to the thermostat may provide the unlimited energy. However, the lifetime increases exponentially as the temperature decreases (see Fig. 6).

33

as in (15). The equality of mean kinetic and potential energies of the

system is proposed. The limit lim(1 1/ x) x e should be used.

x

Exercise 34. The milk shelf live is eight hours at room temperature (T = 300 K) and five days in the fridge (T = 280 K). Define the activation energy and frequency factor of the souring process (see formula (18)).

Exercise 35. Estimate the milk shelf live at T = 320 K (see the previous Exercise).

Slight thermalization accounting

If the energy exchange between the system and thermostat takes place, it can be characterized by the time τth. Here we try to estimate the τth value. Imagine that the thermostat is a buffer gas under the pressure P ~ 100 kPa and at the temperature T ~ 300 K. The atomic concentration can be estimated as follows n ~ P/kBT ~ 1022 m-3. The number of gas atoms colliding with the molecular system with the area S per second is nvS, where v ~ 100 m/s is the characteristic atomic velocity. So, if we estimate the S value as 1000 Å2, then the number of gas atoms is about 107. It means that the averaged time between two collisions, which has the same order as τth, is about 10-7 s. Therefore, τth ~ 100 ns. Of course, the estimated value can vary for different systems in a wide range (usually 100 ps – 10 μs). Note that in the most MD simulations the modeling time belongs to this range. In practice, the relation τ ≈ τth takes place. In this case, the system cannot be regarded as neither microcanonical nor canonical ensemble. So, both equations (18) and (19) are nonapplicable. Let us develop the analytical theory for such systems.

As was mentioned above, the lifetime τ is determined as the average of the lifetimes of several molecules decayed at the same temperature (for thermalized system) or total energy (for the isolated system), but at different initial distributions of the atomic velocities of these molecules. If the number of molecules M0 is sufficiently large, then the number of molecules M(t) non-decomposed in time t decreases exponentially as follows M(t) = M0exp(–t/τ). At a sufficiently large number of statistical tests, the probability density n of finding the molecule in a certain state can be described in the framework of the kinetic equation. For the system contained Nat atoms, the n value is generally a function of 6Nat co-

35

ordinates of the phase space and the time. To solve the considered problem, it suffices to assume that n depends only on the time t and the total

0

equation, it is convenient to consider that the molecules are introduced into the system continuously at a constant rate I rather than simultaneously at the time t = 0. In that case, the initial energy of the system is E0 = CT (or CTm for the isolated system). It is also assumed that the system lifetime is much longer than the characteristic period of its natural oscillations and the characteristic time of the internal heat transfer between its normal modes. The kinetic equation of the particle balance is

where E0 = CT, S(E, T) is the equilibrium distribution density of an individual thermalized molecule in the energy E at the temperature T. To avoid the consideration of the heat transfer processes from the environment to the individual atoms of the molecule, we assumed that the entire cluster is simultaneously thermalized, i.e., the nonequilibrium distribution of its states with the density n(E, t) is transformed in the characteristic time interval τth to the equilibrium one with the density S(E, t). The dependence of the average molecule lifetime τ on the characteristic thermalization time τth and other parameters of interest can be obtained from the stationary solution n0(E) of Equation (20), the left part of which is equal to zero. For the steady-state process, the average lifetime

τ, the total number of the clusters M(t)|t=+∞ in the system, and the rate I of their addition to the system are related as follows

0

Substituting equation (21) into stationary equation (20) (in which the left part is equal to zero), we obtain

36

Integrating the expression (22) with respect to E and taking into account

the equation (21) and the relation S (E,T )dE 1, we obtain the desired

0

dependence of τ on the parameters of the problem in the form

In the harmonic approximation, which is applicable in many cases, the S(E, T) can be expressed as EXexp(–E/T)/(X! TX+1). It is interesting, that the reaction rate depends on τth in the non-monotonic manner (see Fig. 7).

Fig. 7. Non-monotonic dependence of the duration of the propyne isomerization to allene on the characteristic heat exchanging time τth at different temperatures.

This reaction plays an important role in the methane cracking

Exercise 36. Please simplify the expression (23) in the following limits: τth tends to zero and τth tends to infinity. Please compare the expressions obtained with the formulae (18) and (19) and try to explain these results.

Special software for MD simulation

There are many special programs for MD simulations. Such packages as Abinit, CP2K, GAMESS, Gaussian, GROMACS, LAMMPS,

37

Spartan, SIESTA, VASP and many other programs are widely used. Every program has its own type of input file with initial nuclei positions and velocities. It should also contain information about the potential function used, total number of MD steps or stopping criterion, external conditions, etc. This file should be prepared before the MD simulation. During the calculation the program returns nuclei positions, velocities and other data (if required) at the each step of MD simulation. As a result, the obtained data can be visualized by using the same program package or any external software (for example, ClustVis). The permitted syntax for every package should be studied carefully (see the corresponding user manual) before the simulation begins.

Exercise 37. Please visit the Internet homepages of the MD programs listed above. Clarify for every package the following aspects: is it commercial or free; what are the types of potential functions (empirical, semi-empirical, ab initio) supported by the program; does the program have the built-in visualizer. Collect the answers in the table.

How to design the MD simulation

If someone wants to carry out the MD simulation, first of all, he should answer on the following questions.

A.What is the physical process that I want to simulate? What important features of this process should be taken into account? Can I neglect any effects for simplicity? Can I simulate the smaller model of the system for computer resources economy? Is the simulated system large enough for demonstration the similar behavior as the real system?

B.What potential function should I choose? Can it provide the satisfactory accuracy? Does it describe energy, geometry and oscillation frequencies of the relevant molecules correctly? How much computational time can I spend simulating the system? Are my computers productive enough to perform the calculations?

C.What additional conditions should be considered? What physical quantities are conserved (energy, temperature, pressure, volume, number of particles, etc.)? What methods should I employ to simulate these conditions?

D.What software should I use to provide the simulations correctly? Should I combine two or more program packages to simulate the processes considered? Should I use my own programs? What is the realiza-

38

tion of MD algorithm in the chosen software? Is that realization suitable for solving the regarded problem?

E.How many MD time steps should be done? What is the stop criterion for the program?

F.How should I visualize and interpret the results obtained?

A few examples of using MD methods in multiscale modeling

I. Accelerated thermal decay with MD/MD multiscale simulation

In multiscale approaches the system is simulated in various scales, and the lower scales provide necessary information for the higher ones (Fig. 8). At first, we regard the accelerated thermal decay modeling where two MD levels are implemented. The thermal decay of a given molecule at low temperature can be divided in two phases. The first (quasi-equilibrium) phase is characterized by the system oscillations near the equilibrium state for a long time.

Fig. 8. Scheme of the multiscale modeling in solid state physics.

QM – quantum mechanics, MD – molecular dynamics, MC – Monte-Carlo,

DD – dislocation dynamics, SM – statistical mechanics, CA – continuum approximation

39