Механические_колебания_и_волны_Основы_биоакустики
.pdf
ЛЕКЦИЯ № 3
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. БИОАКУСТИКА.
БИОАКУСТИКА
-раздел биофизики, в котором изучают происхождение и свойства звуков, их воздействие на живые организмы.
Актуальность темы:
1. Физической основой биоакустики является теория колебаний и волн, которая универсальна в описании многих процессов в природе. КОЛЕБАНИЯ - это движения или процессы, обладающие той или иной степенью повторяемости во времени.
ВОЛНЫ – перенос энергии колебаний в пространстве.
По физической природе
механические |
электромагнитные |
(связаны с движением)
Описываются сходными уравнениями!!!
2. Слух человека – наиболее важное чувство (с точки зрения социального взаимодействия). Изучение темы является основой физиологии слухового анализатора.
3. Материал темы является основой для изучения ультразвуковых методов исследования и лечения в медицине, понимания действия вибрации и шума на организм.
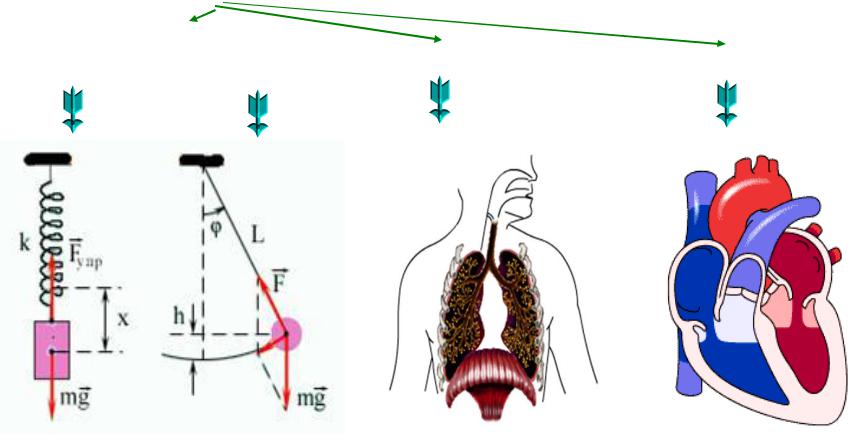
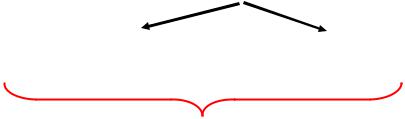
Механические колебания - это движения тела, выведённого из положения равновесия, в ходе которых тело многократно движется по одной и той же траектории, проходя одни и те же точки пространства через равные промежутки времени.
Примеры механических колебаний
пружинный |
математический |
дыхание |
сердцебиение |
|
маятник |
маятник |
|||
|
|
Осцилляции – синоним слова «колебания», который часто встречается в учебной и научной литературе.
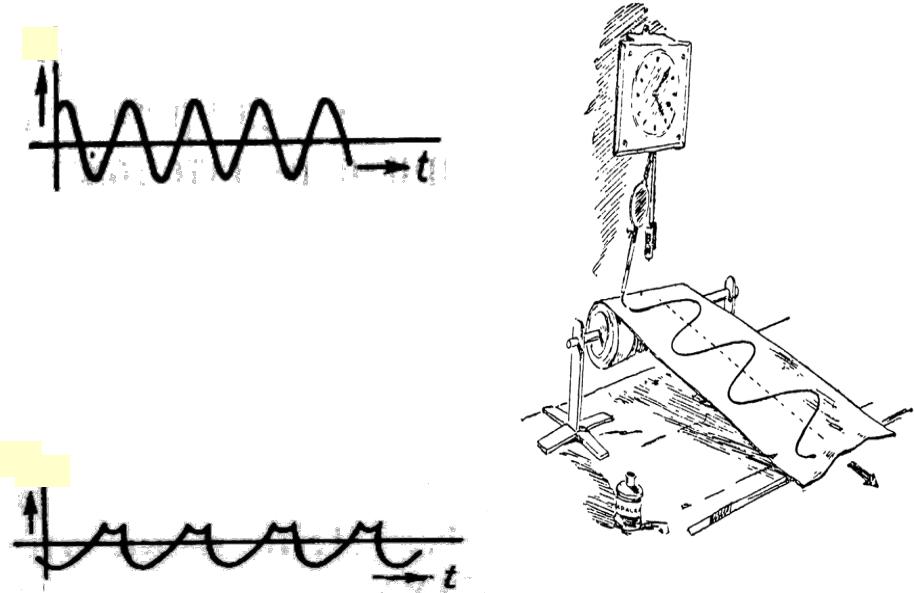
Гармонические колебания - простейший вид колебаний, которые осуществляются по закону синуса (косинуса), т.е. их графиком служит синусоида (косинусоида), а в их уравнение входит функция синус (косинус).
S
Синусоида описывает изменение смещения колеблющегося тела от 
положения равновесия во времени, а не тело движется по синусоиде!
Негармонические колебания не осуществляются по закону синуса или косинуса.
S
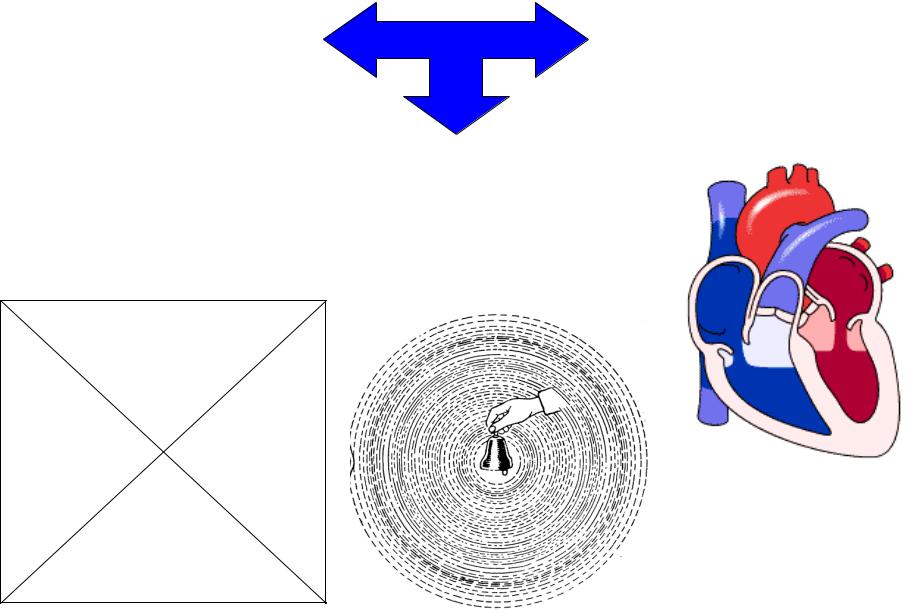
Колебания (в зависимости от источника энергии )
Свободные (собственные)
осуществляются за счёт внутренних сил, возникающих в колебательной системе при однократном выведении её из положения равновесия.
Автоколебания
осуществляются за счёт внутренней энергии системы.
Вынужденные
осуществляются за счёт действия периодической внешней силы.
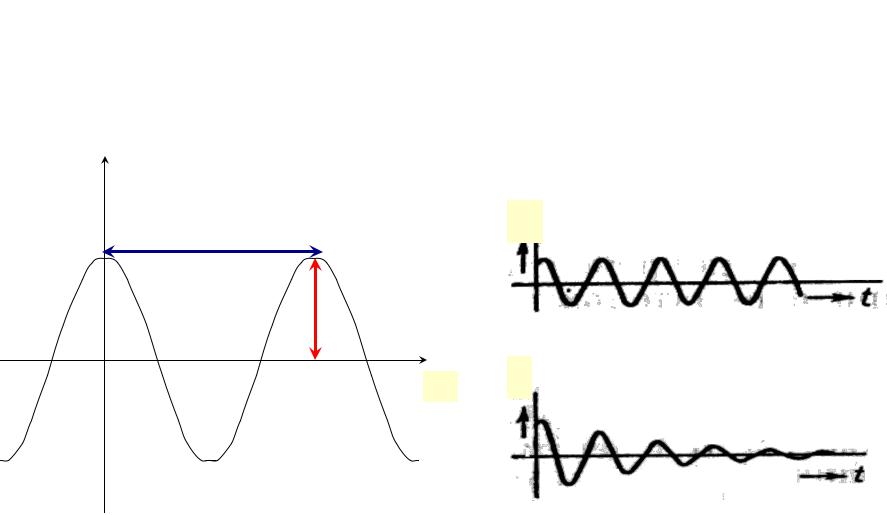
ПАРАМЕТРЫ КОЛЕБАНИЙ
S
ПЕРИОД
AМПЛИТУДА
t
1. Амплитуда колебаний (А) – это максимальное смещение колеблющегося тела от положения равновесия. Измеряется в метрах.
S
Незатухающие колебания
S амплитуда постоянна
Затухающие колебания
амплитуда уменьшается во времени
2. Период колебания (T) – время одного полного колебания. Единицей измерения периода является секунда.
ПАРАМЕТРЫ КОЛЕБАНИЙ
3. Линейная частота колебаний ( ) - число колебаний в единицу времени. Измеряется в Герцах.
|
n |
|
|
1Гц 1 |
кол |
|
|
|
|
||||
|
t |
|
|
|
||
|
|
|
сек |
|||
Т1
Частота и период – физические величины, обратные друг другу.
Т 1
4.Фаза (φ )- свойство колебательного движения, которое характеризует положение колеблющегося тела в любой момент времени в радианах.
5.Угловая скорость, или круговая частота колебаний ( ω) –
число радиан, пройденных колеблющимся телом за единицу времени. Измеряется в рад/с.
2
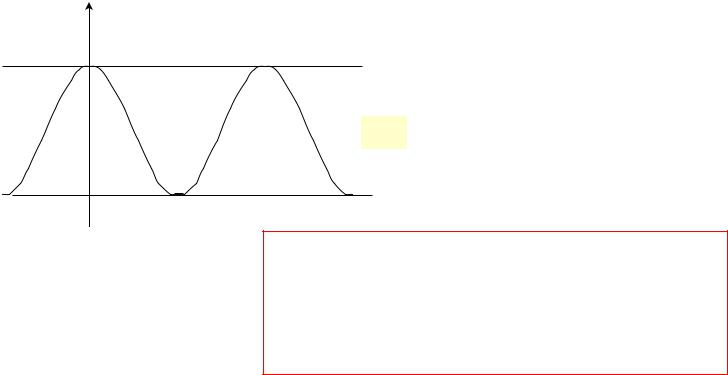
СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Такие колебания мог бы совершать маятник, если бы на него не действовала сила трения.
S
Уравнение свободных незатухающих гармонических колебаний описывает изменение
t смещения колеблющегося тела во времени.
S A sin( 0t 0 )
S A cos( 0t 0 )
S смещение |
0 |
частота |
0 |
начальнаяфаза |
|
A амплитуда |
t время |
||||
|
|
||||
В реальных системах свободные колебания всегда затухающие из-за наличия силы трения, на преодоление которой тратится энергия.
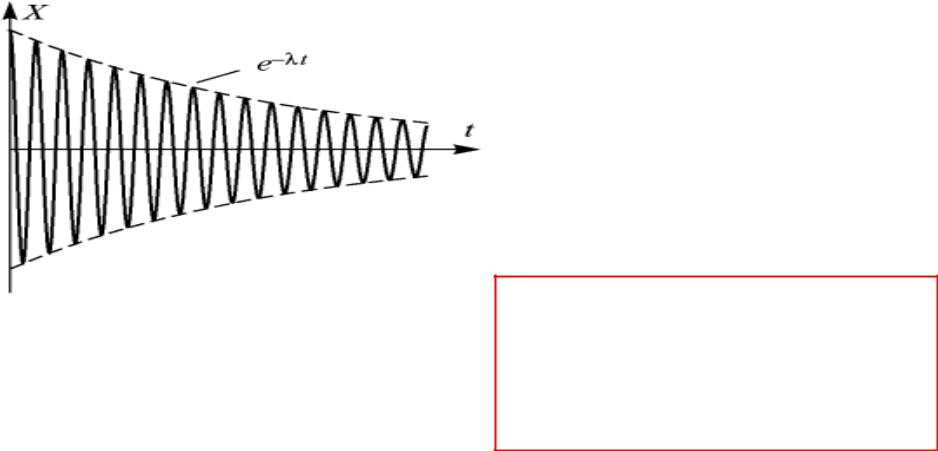
СВОБОДНЫЕ ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
|
|
|
|
A(t) A e t |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
A0 начальнаяамплитуда |
||
|
|
|
|||
|
|
|
Коэффициент затухания (β) – |
||
|
|
|
величина, являющаяся мерой |
||
|
|
|
снижения амплитуды колебаний в |
||
|
|
|
единицу времени. |
||
Уравнение свободных затухающих гармонических 
колебаний
S A0 e t sin( t 0 ) S A0 e t cos( t 0 )
частотазатухающих |
|
|
|
|
|
|
2 |
2 |
|
2 |
|
колебаний |
|
0 |
|
||
|
|
|
|
|
Логарифмический декремент затухания (λ) – величина, являющаяся мерой снижения амплитуды колебаний за один период, натуральный логарифм отношения амплитуд двух последовательных колебаний:
ln |
A(t) |
T |
A(t T ) |
При описании различных процессов (химических и биологических) термин «декремент» всегда означает уменьшение амплитуды.
Пример. Если мы говорим: «Потенциал действия распространяется бездекрементно по нервному волокну», это значит, что его амплитуда в любой точке волокна одинакова.