
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ЭПУ
ОТЧЕТ
по лабораторной работе №4
по дисциплине «квантовая и оптическая электроника»
Тема: Исследование прохождения лазерного излучения через световод
Студенты гр. 7201 |
|
Лукпанов Т. |
|
|
Шапошников В.А |
|
|
Шурыгин А.С. |
|
|
Яковенко Е.В. |
Преподаватель |
|
Ламкин И.А. |
Санкт-Петербург
2020
Цель работы – исследование прохождения лазерного излучения через многоволоконный световод, оптических потерь в световоде, трансформации распределения излучения в сечении лазерного пучка после световода.
Описание лабораторной установки. В данной работе основные исследования проводятся с использованием многоволоконного нерегулярного световода. Установка включает газоразрядный лазер, укрепленный на оптической скамье соосно с входным торцом световода (рис.1). Поворотный столик П1 обеспечивает изменение угла падения (θпад) лазерного пучка на входной торец световода. Мощность пучка, отраженного от входного торца световода Ротр регистрируется фотоприемником ФП1 и измерительным прибором ИП1. При необходимости зарегистрировать полную мощность излучения лазера Рвх фотоприемник ФП1 устанавливается перед световодом. Мощность пучка, прошедшего световод Рвых, регистрируется тем же фотоприемником ФП1, устанавливаемым вплотную к выходному торцу световода. При регистрации мощностей излучения лазера, отраженного и прошедшего световод пучков лазерный луч должен попадать в центр приемной площадки фотоприемника. Снятие радиального распределения интенсивности в поперечном сечении выходного пучка осуществляется с помощью перемещаемого подвижкой П2 точечного фотоприемника ФП2 с диаметром приемного окна порядка 1 мм.
Установка позволяет исследовать также прохождение лазерного излучения через оптические элементы в виде стеклянных параллелепипеда, прутка и трубки. Источником излучения в данном случае служит полупроводниковый лазер видимого диапазона. Эксперименты по передаче изображения базируются на использовании регулярного световода с входной и выходной оптическими системами и экрана.
Оценка степени пространственной когерентности излучения производятся с помощью регулярной дифракционной структуры Д – металлической мелкоструктурной сетки с круглыми отверстиями диаметром d и шагом D по координатам x, y в плоскости сетки. Структура устанавливается поочередно на пути прямого лазерного пучка либо перед световодом, либо – после световода.
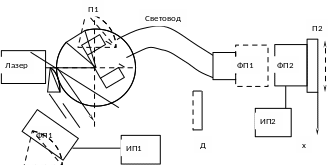
Рис.1. Структурная схема лабораторной установки
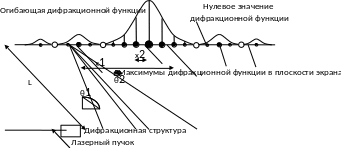
Рис.2. Распределение экстремумов дифракционной функции
Контроль распределения интенсивности в поперечном сечении дифрагированного пучка осуществляется вручную или фотографически (рис.2). Углы дифракционной расходимости θ1 и θ2 могут быть найдены экспериментально по измеренным расстояниям между экстремумами x1, x2 и расстоянию от сетки до экрана L: θ1 ≈ x1 / L, θ2 ≈ x2 / L. Используя известные из теории дифракции соотношения для θ1 ≈ λ / d и θ2 ≈ λ / D, а также их экспериментальные значения, можно оценить размеры дифракционной структуры d и D.

Обработка результатов
Pвх=452 отн. ед.
Табл.1. Зависимость отраженной мощности и коэффициента отражения от угла падения
θпад, град |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
Pотр, отн. ед. |
12,7 |
13,1 |
13,5 |
14,4 |
15,8 |
17,7 |
20,6 |
24,3 |
28,6 |
33,7 |
34,5 |
60,1 |
67,8 |
103 |
139,7 |
ρ |
0,028 |
0,029 |
0,030 |
0,032 |
0,035 |
0,039 |
0,046 |
0,054 |
0,063 |
0,075 |
0,076 |
0,133 |
0,150 |
0,228 |
0,309 |
Табл.2. Зависимость прошедшей (выходной) мощности и коэффициента пропускания от угла падения
θпад, град |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
Pвых, отн. ед. |
215 |
201 |
179 |
160 |
148 |
144,4 |
138,8 |
13,3 |
2,3 |
0,7 |
0,2 |
0 |
τ |
0,476 |
0,445 |
0,396 |
0,354 |
0,327 |
0,319 |
0,307 |
0,029 |
0,005 |
0,002 |
0,000 |
0,000 |
Табл.3. Зависимость коэффициента потерь от угла падения
θпад, град |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
ρ. |
0,028 |
0,029 |
0,030 |
0,032 |
0,035 |
0,039 |
0,046 |
0,054 |
0,063 |
0,075 |
0,076 |
0,133 |
0,150 |
0,228 |
0,309 |
τ |
0,445 |
0,396 |
0,354 |
0,327 |
0,319 |
0,307 |
0,029 |
0,005 |
0,002 |
0 |
0 |
0 |
0 |
0 |
0 |
α |
0,527 |
0,575 |
0,616 |
0,641 |
0,646 |
0,654 |
0,925 |
0,941 |
0,935 |
0,925 |
0,924 |
0,867 |
0,850 |
0,772 |
0,691 |
Табл.4. Распределения интенсивности в поперечном сечении выходного пучка (θ = 0°)
x, мм |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Iвых, отн. ед. |
0,2 |
0,9 |
4,0 |
10,2 |
13,8 |
9,2 |
3,7 |
0,5 |
0,1 |
Табл.5. Распределения интенсивности в поперечном сечении выходного пучка (θ = 10°)
x, мм |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Iвых, отн. ед. |
0,1 |
0,2 |
1,3 |
3,4 |
3,2 |
2,0 |
1,6 |
1,9 |
3,2 |
3,9 |
1,8 |
0,3 |
0,1 |
Табл.6. Распределения интенсивности в поперечном сечении выходного пучка (θ = 20°)
x, мм |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
Iвых, отн. ед. |
0,1 |
0,2 |
0,5 |
1,0 |
1,5 |
0,7 |
0,2 |
0,1 |
0 |
0 |
0,1 |
0,2 |
0,3 |
1,0 |
1,2 |
0,5 |
0,1 |
0 |
Формулы для расчета:
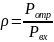
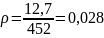
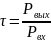
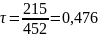
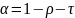
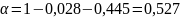
Расчет средних значений диаметра отверстий d и шага D дифракционной структуры.
x1=28 мм
x2=3 мм
L=250 мм
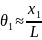
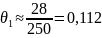
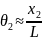
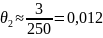
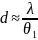
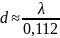
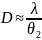
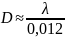
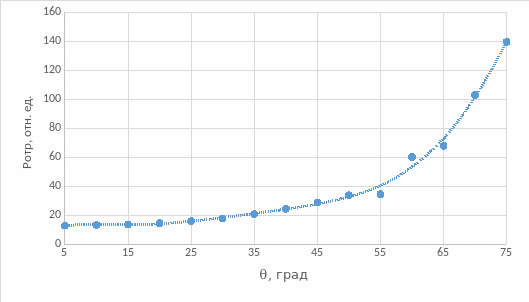
Рис.3. Зависимость отраженной мощности и от угла падения
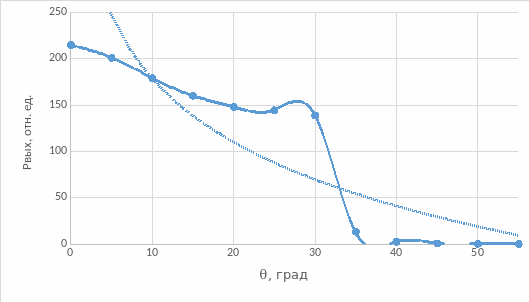
Рис.4. Зависимость прошедшей (выходной) мощности от угла падения
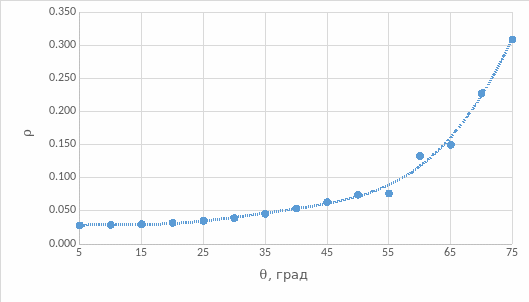
Рис.5. Зависимость коэффициента отражения от угла падения
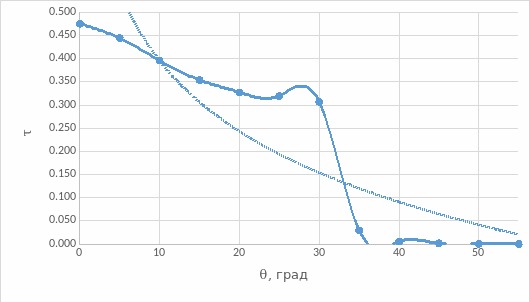
Рис.6. Зависимость коэффициента пропускания от угла падения
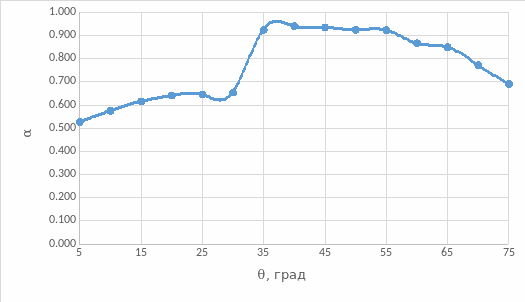
Рис.7. Зависимость коэффициента потерь от угла падения

Рис.8. Распределения интенсивности при θ = 0°
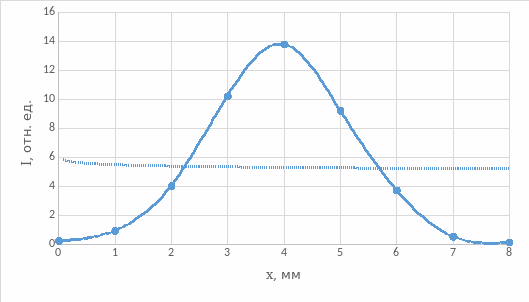
Рис.9. Распределения интенсивности в поперечном сечении выходного пучка при θ = 0°

Рис.10. Распределения интенсивности при θ = 10°
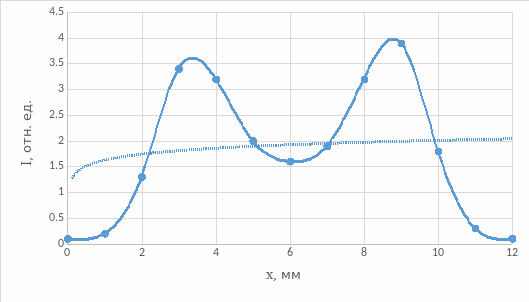
Рис.11. Распределения интенсивности в поперечном сечении выходного пучка при θ = 10°

Рис.12. Распределения интенсивности при θ = 20°
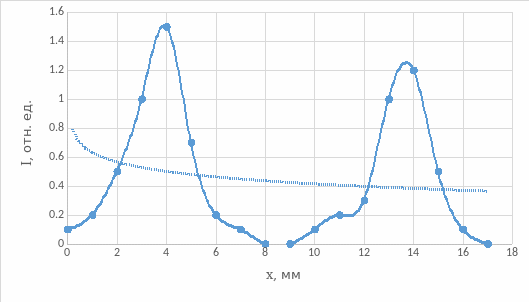
Рис.13. Распределения интенсивности в поперечном сечении выходного пучка при θ = 20°
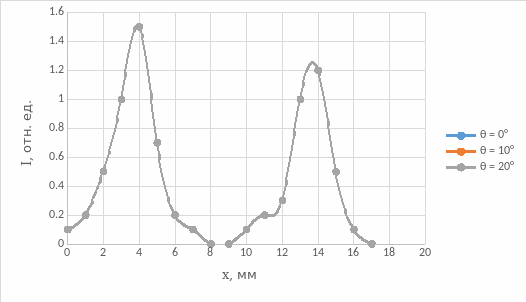
Рис.14. Распределения интенсивности в поперечном сечении выходного пучка

Рис.15. Распределение интенсивности пучков за дифракционной решеткой при L=250 мм
Вывод: из рис. 3 и 5 видно, что при увеличении угла падения отраженная мощность и коэффициент отражения экспоненциально растут. Из рис. 4 и 6 видно, что при увеличении угла падения прошедшая (выходная) мощность и коэффициент пропускания вначале плавно, а затем резко (ступенчато) уменьшаются. Из рис.7 видно, что при увеличении угла падения коэффициент потерь вначале плавно увеличивается (рост коэффициента потерь определяет уменьшение с ростом угла падения коэффициента пропускания), затем он резко увеличивается (за счет резкого уменьшения коэффициента пропускания), а затем уменьшается (на этом участке спад коэффициента потерь связан с увеличением коэффициента отражения, коэффициент пропускания равен нулю). Из рис. 9 видно, что распределения интенсивности в поперечном сечении выходного пучка при θ = 0° имеет колоколообразный вид. Из рис. 10 видно, что распределения интенсивности в поперечном сечении выходного пучка при θ = 10° уже имеет два перекрывающихся максимумов, при том максимальные значения интенсивности в данном случае меньше, чем при θ = 0°. При θ = 20° эти максимуму расползаются и не перекрываются, максимальные значения интенсивности в данном случае меньше, чем при θ = 10°. На рис.15 видно распределение интенсивности пучков за дифракционной решеткой. Оценить параметры d и D дифракционной решетки мы не можем, так провели измерение только при L=250 мм (не сможем решить систему уравнений) и не знаем длину волны лазера.
