

1. Классификация ИС по степени интеграции. Закон Мура. Прогноз развития микроэлектроники на ближайшие годы. (ITRS – International Technology Roadmap for Semicondactor).

2. Усилитель бегущей волны как базовый элемент функциональной СВЧ микроэлектроники: принцип действия, элементы конструкции
Усилитель на БВ реализуется за счет нарастания волн пространственного заряда, распространяющихся от входного к выходному БШ в среде обладающей отрицательной дифференциальной подвижностью. Свойства такой среды определяются зависимостью средней скорости дрейфа электронов от напряженности электрического поля.
Арсенид Галия хорош тем, что у него есть так называется область отрицательной дифференциальной подвижности. ОДП возникает из-за то го что арсенид Галия является прямозонным полупроводником с несколькими долинами.
Энергетическая Диаграмма арсенида Галия.
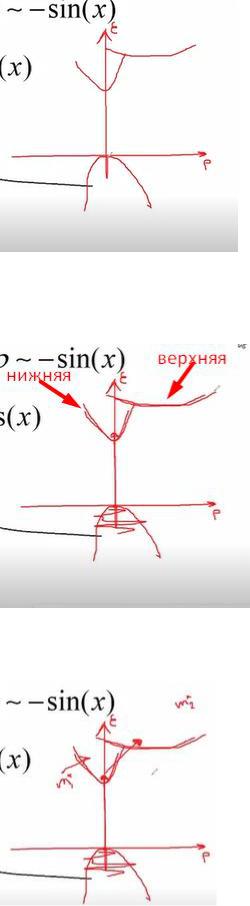
По мере того, как мы подаем на арсенид галия потенциал, и заряжаем электроны, находящиеся внизу (в валентной зоне). Электроны начинают приобретать энергию достаточную для того, чтобы преодолеть запрещённую зону и попасть в зону проводимости (наверх). При этом зона проводимости у арсенида галия состоит из двух долин. Нижняя долина имеет более крутые склоны. Верхняя долина более высокоэнергетиченая более пологая.
Соответственно электроны с относительно небольшой энергии попадают в нижнюю долину, но если энергии достаточно много сообщается электрону, то они могут попасть уже в верхнюю долину. Но за счёт того, что форма долины нижней и верхней разная, то эффективная масса электрона в долине снизу и сверху отличаются. Так что М1 меньше чем м2 (верхняя )
А раз эффективная масса электронов становится больше с ростом энергии то и скорость дрейфа этих электронов становится меньше. Это говорит о том, что подвижности электронов, попадающих в верхнюю долину, резко падает. То есть пока у нас энергия электронов маленькая, т.е. поле маленькое, подвижность большая, потому что электроны лёгкие. После того как энергия начинает увеличиваться так что отдельный электрон уже способный попадать в зону с низкой подвижностью. То поле скоростная характеристика начинает изменяться и выходить на максимум. (Точка называет критическим полем Екр порядка 3.5 кВ на см).

После этого на характеристики возникает перегиб, и мы видим спадающий участок. И на этом участке подвижность электрона начинает падать. Он называется область отрицательной дифференциальной подвижности. Т.е. дифф подвижность в этой части <0. С ростом энергии подвижность электронов падает, а значит и скорость дрейфа с ростом энергии, ростом поля снижается.
Коэффициент анизотропии.
µс -статическая подвижность, те скорость дрейфа на напряженность Эл поля. (Та самая, когда мы говорили о распространении (дрейфе) электронов в различных материалах). µддифференциальная подвижность дv/дЕ |Е=Е0.
Рассмотрим поле скоростную характеристику гаас (АРСЕНИД Галия используется в качестве основного П/П с ОДП). Видно, что есть область нарастания максимум и область убывания, которая плавно переходить обратно в область нарастания. Чтобы рассчитать статическую подвижность надо соединить начало координат с точкой в которой мы хотим знать эту подвижность и посмотреть какой угол будет получаться. И тангенс этого угла будет равен µс.
Везде угол острый, везде подвижность имеет положительное значение.
Дифференциальная подвижность. Геометрически ее нахождение — это надо проводить касательную (зелёная штриховая линия) и посмотреть угол тетта 2. Если проводим к точке на нарастающей части кривой, то угол тетта 2 острый и µд будет положительная. Если говорить о точках, где спадающий характер зависимости µд будет отрицательная.

(Опечатка в слайде ) к<0 , коэффициент анизотропии отрицательный.
Т.е. при переходе через напряженность электрического поля равной критической, КОЭФФИЦИЕНТ анизотропии меняет свой знак. Сначала положительный потом ноль в максимуме потом отрицательный.
Вобласти линейного нарастания (начало характеристики), т.е. там, где пока скоростная характеристика имеет ещё линейный характер, статическая и динамическая подвижность не смотря на разные формулы имеют одно значение. Т.к. линейная характеристика и здесь коэффициент анизотропии равен 1. Это нужно чтобы проанализировать решение дисперсионного уравнения.
Воснове работы большинства волновых приборах (работающих на бегущих волнах) лежит дисперсионная характеристика. Чаще всего дисперсией для микроволновой электроники называют законы или формулу связывающую между собой частоту и волновое число или частоту и постоянную распространения (принципиально одно и то же что волн число).
Как вариант записи дисперсионного уравнения. Некая функция связывающая амега и гамма. Амега-частота, гамма-постоянная распространения. И они равны 0. Зная закон дисперсии, большинство рабочих характеристик приборов можно посчитать. Записываем уравнение, описывающее волновой процесс.
Это амплитуда*експ^гамма*р. Гамма-постоянная распространения. Дальше если гамму предоставим как комплексную число постоянной амплитудной и фазовой Альфа и бетта. То можно поделить уравнение на 2 экспоненты и получим что у нас есть фчх (постоянная фазовая на расстояние пройденное бетта (зависит от амега)*р) и АЧХ (амплитудная постоянная (зависит от амега на расстояние и это показатель эксп). Можно посчитать групповую скорость и время задержки взяв производную. Дбетта/дамега.
Т.е. зная закон дисперсии можно выразить гамму от амега и посчитать ачх, фчх, групповую скорость.

Если говорить о УБВ разбираемся только с ачх. Те какой коэффициент усиления или ослабления у прибора на данной частоте или диапазоне.
ДИСПЕРСИОННОЕ УРАВНЕНИЕ ВОЛН ПРОСТРАНСТВЕННОГО ЗАРЯДА В ПП
Релаксационная частота — это величина обратно пропорциональная времени, в течение которого амплитуда колебаний затухает в е раз. Частота это просто 1/тау, где тау -время затухания сигнала в е раз. Для каждого типа волны релаксационная частота рассчитывается по-своему. На слайде это сигма(проводимость)/диэлектрической ПРОНИЦАЕМОСТЬ П/П. Сигма это qnµ, где n это концентрация носителей заряда, µ-подвижность этих зарядов. По сути, релаксационная частота
— это характеристика того с какой скоростью затухают колебания. Дельта - параметр, учитывающий асимметрию структуры убв.
(В нижней формуле не гамма, а фигня на е похожая). Это поперечное волновое число, т.е. т.к.
структура имеет некоторую толщину (пленка п/п-ая), то в ней реализуется некоторое распределение электрического потенциала и это распределение характеризуется поперечным волновым числом.
Также введено 2 обозначения: беттар и беттае по размерности соответствуют фазовой постоянной.
Чтобы понять, как распространяются волны имея в виду такое ДИСПЕРСИОННОЕ УРАВНЕНИЕ. Надо вывести как гамма зависит от амега попытаться найти как запись альфа, бетта от амега. Как зависят постоянная распространения, амплитудная и фазовая от частоты. По сути, решаем уравнение.
Решение дисперсионного уравнения позволит понят как зависит коэффициент усиления усилителя от частоты.
Надо перейти к бездиффузионному приближению и приравнять Д (коэф. диффузии) к 0. Первое слагаемое равно нулю и останется форма дисперсионного уравнения в нулевом приближении.
Для нахождения связи гамма и амега а также значения альфа(амега) и бетта(амега) Уравнение у нас линейное. Слева единственное слагаемое с гамма, его оставляем слева остальное направо и делим на v0. Дальше если гамма будет иметь форму альфа+iбетта то две части уравнения выглядят так:

Где бетта е это частота на фазовую постоянную. Если это выражение, представляющее собой постоянную распространения подставить в показатель экспоненты у бегущей волны, раскрываем скобки и получаются две эксп. Где часть с беттае на р фчх. Первая экспонента это ачх. Отсюда можно найти фазовую скорость. Фазовая скорость для любой волны это амега/фазовую постоянную (бета е). (Скорость распространения волны ранее скорости дрейфа электронов!)
С какой скоростью электрон дрейфует с такой скоростью и происходит распространение волны. Так как бетае>0 то волна прямая (в нулевом приближении только прямая волна) Существуют различные моды прямой волны. Т.к. дельта (в первой экспоненте) никуда не делась. А она зависит от поперечного волнового числа. То мы можем наблюдать различные моды этой прямой волны с таким решением.
Если напряженность постоянного электрического поля больше критического, то величина (каппа) имеет знак минус. Т.е. весь показатель экспоненты отрицательный. А раз отрицательное то вся экспонента нарастает. Те по мере распространения волны (роста р) амплитуда волны начинает расти благодаря тому, что постоянная нарастания имеет отрицательный знак.
Дельта зависит от частоты таким образом что с ростом частоты величина альфа (постоянной нарастания) достигает максимального значения и выходит в насыщение. По сути, максимальное значение Альфа не может превышать модуля |каппа на бетта р | (бетта р это отношение амегар
/в0).
Из всего этого можно построить амплитудно-частотную характеристику.
МОДЫ В БЕЗДИФФУЗИОННОМ ПРИБЛИЖЕНИИ

Из всего этого можно построить амплитудно-частотную характеристику. По сути, мы наблюдаем набор мод. Для каждой моды постоянная нарастания альфа, или коэффициент усиления усилителя с частотой нарастает. Для любой моды нулевой, первой и т.д. видно нарастание и выход в насыщение, все выходят в насыщение с альфа равным одинаковому значению (каппа на беттар).
Для всех мод существует критическая частота. Если частота соответственная этой моде ниже, чем критическая, то не смотря на отрицательный КОЭФФИЦИЕНТ анизаторопии волны все равно будет затухать. Замечание: нулевая мода (низшая и основная для усилителя бегущей волны на волнах пространственного заряда, потому что она начинает работать с 0 гц и работает во всем доступном диапазоне) для нее критическая частота=0, а раз так частот ниже, чем 0 мы не знаем, то нулевая мода усиливает во всем диапазоне частот. В то время как более высшие моды работают в режиме усиления только при достаточно высоких частотах. Значения критически частоты для разных мод мб рассчитаться по формуле:
Где Величина беттае*а критическое значение этого произведения. n - номер моды. Максимальный коэффициент усиления или максимальное значение амплитудной постоянной будет у всех одинаковое (каппа*беттар).
Что представляют собой отдельно взятые моды. Моды для любых волн — это различные распределения волн по толщине рассматриваемой структуры.
ВЛИЯНИЕ ДИФФУЗИИ. УСИЛЕНИЕ С УЧЁТОМ ДИФФУЗИИ.(объяснение на 5)
Здесь все не так просто потому, что мы можем рассматривать при распространении волны 2 вида диффузии. Диффузия продольная и поперечная.
(Синее - волна, зелёное - волноведущая среда) можем наблюдать Диффузию продольную j|| - продольный ДИФФУЗИОННЫЙ ток, он будет перемешать заряды из области, где их много в область, где их мало. Но мы должны помнить, что существует поперечный ДИФФУЗИОННЫЙ ток. Т.е. из синей области электроны могут идти наверх, однако важно понимать, что по мере распространения волны поперечная составляющая диффузионного тока она для нас не имеет большой проблемы. Потому что когда мы принимаем волну, по сути, мы смотрим сколько электронов просто под барьером Шоттки и то, что они растянулись вверх и вниз не имеет большого значения. Потому что амплитуда колебания по длине в направлении оси х, она не меняется, т.е. где их было много, там их много и осталось, они просто в конкретно этом сечении определены в большем объеме П/П (по большему сечению). В то время как продольная составляющая j|| она играет роль крайне негативную.
Векторная сумма продольной и поперечной составляющей будет составлять суммарный диффузионный ток и имеет этот ДИФФУЗИОННЫЙ ток будет определяться коэффициентом ДИФФУЗИИ. Поэтому если волна распространяется в объеме П/П, то может существовать как

поперечная, так и продольная составляющие и их сумма обязательно должна быть равна ДИФФУЗИОННОМУ. Т.е. ДИФФУЗИОННЫЙ ток суммарный будет определяться свойствами структуры. А соотношение продольной поперечной компонент определяться условиями, в которых распространяется волна. Если волну прижать к поверхности рисунок справа) то поперечная составляющая поскольку тут будет граница раздела (голубой выше это Дэ) значит вверх электроны уже практически не пройдут. Поэтому ДИФФУЗИОННая составляющая поперечная будет практически нулевая. Продольная составляющая при этом увеличится, поскольку сам итоговый суммарный коэффициент диффузии не поменялся. Поэтому при условии, когда волна прижата к поверхности и поперечная составляющая ДИФФУЗИОННОго тока практически равна 0, то можно говорить о том, что продольная составляющая, негативно влияющая на распространение волны, она равна самому ДИФФУЗИОННОМУ ТОКУ, по сути, продольная составляющая и определяется коэффициентом ДИФФУЗИИ.
Мы уже не можем выкинуть КОЭФФИЦИЕНТ диффузии из дисперсионного уравнения. Должны решать с его учётом, но помнить, что если волна распространяется вблизи с границей раздела, то коэффициент диффузии определяет именно продольную составляющую тока те весь коэффициент диффузии влияет на коэффициент усиления. Если мы говорим о потоке электронов, располагающихся в глубине, то можно сказать, что продольная составляющая здесь не так велика и нам нужно будет что-то сделать с коэффициентом ДИФФУЗИИ чтобы уменьшение продольной составляющей учесть. По сути, надо будет использовать уменьшенный КОЭФФИЦИЕНТ диффузии. В любом случае надо модифицировать ДИСПЕРСИОННОЕ УРАВНЕНИЕ с учётом коэффициента диффузии. Эти два приложения носят два названия:
1)где в глубине структуры -свободная граница, те границам потока ничем не ограничена, никак не ХАРАКТЕРИСТИКи не заданы, границам свободная. Так же как в прикладной механики, когда стержень не закреплён, свободный конец.
2)жёсткая граница-при жёсткой границе поток электронов его характеристики строго определены, из-за того, что есть граница, он распространяется рядом с ней. Поперечная составляющая невозможна. Аналогия, когда стержень закреплён.
ЖЁСТКАЯ ГРАНИЦА ДИСПЕРСИОННОЕ УРАВНЕНИЕ:
Это то же уравнение что и на первых слайдах ток поделенное на D. Беттар с чертой-нормированная беттар с учётом 1+дельта.
Решаем квадратное уравнение, следовательно, 2 решения.
Первая часть это постоянная нарастания альфа, вторая часть фазовая постоянная бета. Рассмотрим фазовую постоянную для конкретной моды (н ой). Здесь знак +, это говорит о том, что ваша по-прежнему распространяется в прямом направлено.

Т.е. одна из волн которая возбуждается в такой структуре является прямой волной, при этом дробь стремится чаще всего к 0. За счёт того, что беттад она обычно имеет очень большое значение и если на него поделить произведение каппа на беттарн то получается очень маленькая величина и по сути фазовая постоянная для случая учёта ДИФФУЗИИ она все равно остаётся беттае.
Это говорит о том, что даже при условии учёта коэффициент диффузии скорость распространения волны все равно останется скоростью дрейфа электронов. (Скорость распространения волны не меняется при учете коэффициента диффузии).
А меняется величина амплитудной постоянной (альфа н пр). Помимо каппы на беттар появляется слагаемое беттае ^2/бетад. Чтобы происходили усиление произведение Кана на беттар должно быть отрицательным. А частная бета е квадрат на бета д положительная. Поэтому, когда суммируют то альфа н начинает стремиться к 0. Те КОЭФФИЦИЕНТ усиления начинает так же стремится к 0. Более того если отношение беттае на бетад оказывается больше, чем каппа на беттар то альфа становится положительным и коэф усиления превращается в КОЭФФИЦИЕНТ ослабления.
Т.о. с учётом диффузии мы должны всегда помнить о том, что диффузия усиление уменьшает. Наличие ДИФФУЗИОННОго тока она узнает процесс усиления. Бетае пропорциональна частоте сигнала, который распространяется в П/П. С ростом частоты беттае растет соответственно и дробь становится больше, поэтому альфа становится (по сути, больше) все ближе к 0, поэтому ещё один вывод: с ростом частоты амплитудная постоянная будет стремиться к 0 и даже может стать положительной. Для любой моды 0,1,2,3 с ростом частоты ВЛИЯНИЕ ДИФФУЗИИ увеличивается. Потому что в амплитудной постоянной возникает дополнительная постоянная, которая все это дело объясняет. Спадание достаточно быстрое.
Если говорить о условиях жёсткой границе. Когда КОЭФФИЦИЕНТ диффузии для данного конкретного случая будет равен коэффициенту диффузии из справочника или измерен экспериментально, то мы можем наблюдать второе решение.
По сути, это вторая волна, которая может распространяться по такой структуре, которая возбуждается в любом случае (при возбуждении в принципе волн пространственного заряда ВОЗНИКАКТ знакперед фазовой постоянной, что говорить о том, что волна у нас обратная.
Т.е. если (на рисунке краснон) у нас стоит элемент возбуждения то, снизу появляется обеденная область и она начинает, с одной стороны, гнать волну прямую которая усиливается за счёт отрицательного значения капа на относительно низких частотах. И есть обратная волна она так же одновременно возбуждается. Обратная волна — это волна, у которой фазовая постоянная меняется, в одну сторону с прямой волной, а групповая скорость в другую или наоборот.
Будет распространяться обратная волна и она направлена, а сторону противоположную дрейфу электронов. Если для прямой волны электроны движутся в право (от истока к стоку), то для обратной волны дрейф электронов будет все туда же, а фаза меняться в другую сторону. При этом за счёт того, что величина бета д а в данном случае она является параметром Альфа, а бета е параметром бета (фазовая), за счёт большого значения бета д, она будет быстро-быстро затухать. По сути длинного распространения для обратной волны не возникает, она затухает.
