
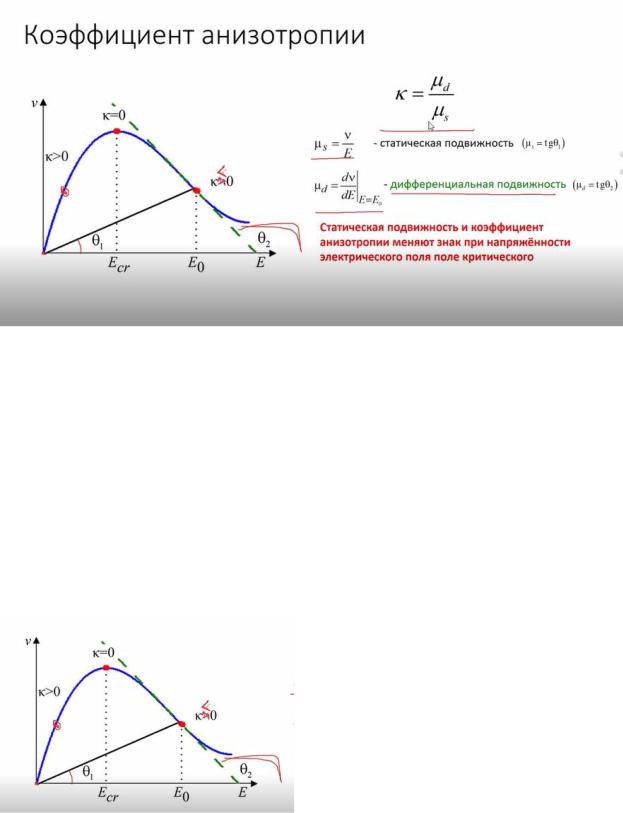
µс -статическая подвижность, те скорость дрейфа на направленность Эл поля. (Там самая, когда мы говорили о распространении (дрейфе) электронов в различных материалах). µд-дифференциальная подвижность дv/дЕ |Е=Е0.
Рассмотрим поле скоростную характеристику гаас (АРСЕНИД Галия используется в качестве основного П/П с отрицдифподвиж). Видно, что есть область нарастания максимум и область убывания, которая плавно переходить обратно в область нарастания. Чтобы рассчитать статическую подвижность надо соединить начало координат с точкой в которой мы хотим знать эту подвижность и посмотреть какой угол будет получаться. И тангенс этого угла будет равен µс.
Везде угол острый, везде подвижность имеет продолжительное значение.
Дифференциальная подвижность. Геометрически ее нахождение — это надо проводить касательную (зелёная штриховая линия) и посмотреть угол тетта 2. Если проводим к точке на нарастающей части кривой, то угол тетта 2 острый и µд будет положительная. Если говорить о точках, где спадающий характер зависимости µд будет отрицательная.
(Опечатка в слайде ) к<0 , коэффициент анизотропии отрицательный.
Т.е. при переходе через напряженность электрического поля равной критической, КОЭФФИЦИЕНТ анизотропии меняет свой знак. Сначала положительный потом ноль в максимуме потом отрицательный. В области линейного нарастания (начало характеристики), т.е. там, где пока скоростная характеристика имеет ещё линейный характер, статическая и динамическая подвижность не смотря на разные формулы имеют одно значение. Т.к. линейная характеристика и здесь коэффициент анизотропии равен 1. Это нужно чтобы проанализировать решение дисперсионного уравнения.
Решение дисперсионного уравнения позволит понят как зависит коэффициент усиления усилителя от частоты.

Надо перейти к бездиффузионному приближению и приравнять Д (коэф. диффузии) к 0. Первое слагаемое равно нулю и останется форма дисперсионного уравнения в нулевом приближении.
Для нахождения связи гамма и амега а также значения альфа(амега) и бетта(амега) Уравнение у нас линейное. Слева единственное слагаемое с гамма, его оставляем слева остальное направо и делим на v0. Дальше если гамма будет иметь форму альфа+iбетта то две части уравнения выглядят так:
Где бетта е это частота на фазовую постоянную. Если это выражение, представляющее собой постоянную распространения подставить в показатель экспоненты у бегущей волны, раскрываем скобки и получаются две эксп. Где часть с беттае на р фчх. Первая экспонента это ачх. Отсюда можно найти фазовую скорость. Фазовая скорость для любой волны это амега/фазовую постоянную (бета е). (Скорость распространения волны ранее скорости дрейфа электронов!)
С какой скоростью электрон дрейфует с такой скоростью и происходит распространение волны.
Так как бетае>0 то волна прямая (в нулевом приближении только прямая волна) Существуют различные моды прямой волны. Т.к. дельта (в первой экспоненте) никуда не делась. А она зависит от поперечного волнового числа. То мы можем наблюдать различные моды этой прямой волны с таким решением.
Если напряженность постоянного электрического поля больше критического, то величина (каппа) имеет знак минус. Т.е. весь показатель экспоненты отрицательный. А раз отрицательное то вся экспонента нарастает. Те по мере распространения волны (роста р) амплитуда волны начинает расти благодаря тому, что постоянная нарастания имеет отрицательный знак.
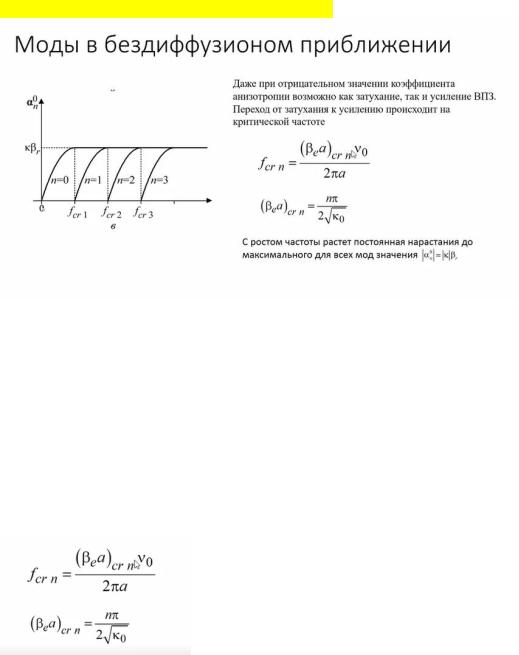
Дельта зависит от частоты таким образом что с ростом частоты величина альфа (постоянной нарастания) достигает максимального значения и выходит в насыщение. По сути, максимальное значение Альфа не может превышать модуля |каппа на бетта р | (бетта р это отношение амегар /в0). Из всего этого можно построить амплитудно-частотную характеристику.
МОДЫ В БЕЗДИФФУЗИОННОМ ПРИБЛИЖЕНИИ
Из всего этого можно построить амплитудно-частотную характеристику. По сути, мы наблюдаем набор мод. Для каждой моды постоянная нарастания альфа, или коэффициент усиления усилителя с частотой нарастает. Для любой моды нулевой, первой и т.д. видно нарастание и выход в насыщение, все выходят в насыщение с альфа равным одинаковому значению (каппа на беттар).
Для всех мод существует критическая частота. Если частота соответственная этой моде ниже, чем критическая, то не смотря на отрицательный КОЭФФИЦИЕНТ анизаторопии волны все равно будет затухать. Замечание: нулевая мода (низшая и основная для усилителя бегущей волны на волнах пространственного заряда, потому что она начинает работать с 0 гц и работает во всем доступном диапазоне) для нее критическая частота=0, а раз так частот ниже, чем 0 мы не знаем, то нулевая мода усиливает во всем диапазоне частот. В то время как более высшие моды работают в режиме усиления только при достаточно высоких частотах. Значения критически частоты для разных мод мб рассчитаться по формуле:
Где Величина беттае*а критическое значение этого произведения. n - номер моды.
Максимальный коэффициент усиления или максимальное значение амплитудной постоянной будет у всех одинаковое (каппа*беттар).
Что представляют собой отдельно взятые моды. Моды для любых волн — это различные распределения волн по толщине рассматриваемой структуры.

Индексы у номера моды определяются функциями, которые описывают распределение если мы говорим об электромагнитной волне электрического магнитного поля. Мы будем рассматривать распределение электрического потенциала волны пространственного заряда. Особенность заключается в том, что они распространяться в сильно асимметричной структуре, т.е. внизу у этой структуры полупроводниковая подложка и если волноведущая структура это гаас то и подложка гаас. На поверхности у него либо диэлектрик, либо воздух, либо где-то металлизация, поэтому структура очень сильно асимметричная и изза этого мы не можем использовать только синус или только косинус.
Для случая бездиффузионного (нулевое приближение) мы обязаны использовать сумму синуса и косинуса, описывающих распределение потенциала в структуре (и Син и кос учитываются при расчете распределения).
Из-за этого получаются интересные картинки. Наверху нулевая мода. С ростом частоты там происходит наклон этой характеристики, фактически только с одной стороны, с другой очень мало влияет на потенциал в нижней части пленки. С ростом частоты как обычно и бывает в любых волноведущих структурах потенциал фокусируется внутри волноведущей структуры и его практически не остаётся снаружи. Если говорим о низких частотах, то потенциал п/п-ой пленки, снаружи бы мы видели экспоненциальное спадение. Для более высоких все равно есть экспоненциальное спадение этого потенциала.
На высоких частотах поперечное волновое число настолько маленькое что потенциал на поверхности будет практически равен 0 и снаружи не увидим никакого потенциала. Т.о. если потенциал волны не высовывается наружу из волноведущей структуры (в данном случае из пленки ПП) не возбудить не принять этот сигнал мы эффективно на можем, поэтому для высоких частот, не смотря на то что дисперсионная характеристика говорить о том что коэффициент усиления будет фиксированный, на самом деле если мы соберем итоговое устройство эффективно возбудить такие колебания (эффективно принять) на таких высоких частотах мы уже не сможем поэтому сам по себе прибор на совсем высоких частотах работать не будет.

Если говорить о структурах с более высоким значением мод (на рисунке н = 1 нижние графики), то видим что распределение имеет более сложный характер, имеет перегиб. В общем здесь что на низких что на высоких частотах значение потенциала вблизи поверхности ПП имеет маленькое значение ив общем не очень хорошо такая мода возбуждается. При этом мода 1-2-3я все имеют дополнительный перегиб, более высокого порядка мода будет иметь, к примеру не один, а ещё один перегиб. Но, по сути, на поверхности будет иметь практически нулевой потенциал, и он не позволит нам не возбудить не принять эффективно эту могу не на низких не на высоких частотах. Поэтому из-за сложности с возбуждением и приемом чаще всего и наиболее эффективно устройство работает именно за счёт низшей (нулевой) моды, а не мод более высокого порядка, их влияние на процесс распространения волн достаточно не велик.
ВЛИЯНИЕ ДИФФУЗИИ. УСИЛЕНИЕ С УЧЁТОМ ДИФФУЗИИ.(объяснение на 5)
Здесь все не так просто потому, что мы можем рассматривать при распространении волны 2 вида диффузии. Диффузия продольная и поперечная.
(Синее - волна, зелёное - волноведущая среда) можем наблюдать Диффузию продольную j|| - продольный ДИФФУЗИОННЫЙ ток, он будет перемешать заряды из области, где их много в область, где их мало. Но мы должны помнить, что существует поперечный ДИФФУЗИОННЫЙ ток. Т.е. из синей области электроны могут идти наверх, однако важно понимать, что по мере распространения волны поперечная составляющая диффузионного тока она для нас не имеет большой проблемы. Потому что когда мы принимаем волну, по сути, мы смотрим сколько электронов просто под барьером Шоттки и то, что они растянулись вверх и вниз не имеет большого значения. Потому что амплитуда колебания по длине в направлении оси х, она не меняется, т.е. где их было много, там их много и осталось, они просто в конкретно этом сечении определены в большем объеме П/П (по большему сечению). В то время как продольная составляющая j|| она играет роль крайне негативную.
Векторная сумма продольной и поперечной составляющей будет составлять суммарный диффузионный ток и имеет этот ДИФФУЗИОННЫЙ ток будет определяться коэффициентом ДИФФУЗИИ. Поэтому если волна распространяется в объеме П/П, то может существовать как поперечная, так и продольная составляющие и их сумма обязательно должна быть равна ДИФФУЗИОННОМУ. Т.е. ДИФФУЗИОННЫЙ ток суммарный будет определяться свойствами структуры. А соотношение продольной поперечной компонент определяться условиями, в которых распространяется волна. Если волну прижать к поверхности рисунок справа) то поперечная составляющая поскольку тут будет граница раздела (голубой выше это Дэ) значит вверх электроны уже практически не пройдут. Поэтому ДИФФУЗИОННая составляющая поперечная будет практически нулевая. Продольная составляющая при этом увеличится, поскольку сам итоговый суммарный коэффициент диффузии не поменялся. Поэтому при условии, когда волна прижата к поверхности и поперечная составляющая ДИФФУЗИОННОго тока практически равна 0, то можно говорить о том, что продольная составляющая, негативно влияющая на распространение волны, она равна самому ДИФФУЗИОННОМУ ТОКУ, по сути, продольная составляющая и определяется коэффициентом ДИФФУЗИИ.
Мы уже не можем выкинуть КОЭФФИЦИЕНТ диффузии из дисперсионного уравнения. Должны решать с его учётом, но помнить, что если волна распространяется вблизи с границей раздела, то коэффициент диффузии определяет именно продольную составляющую тока те весь коэффициент диффузии влияет на

коэффициент усиления. Если мы говорим о потоке электронов, располагающихся в глубине, то можно сказать, что продольная составляющая здесь не так велика и нам нужно будет что-то сделать с коэффициентом ДИФФУЗИИ чтобы уменьшение продольной составляющей учесть. По сути, надо будет использовать уменьшенный КОЭФФИЦИЕНТ диффузии. В любом случае надо модифицировать ДИСПЕРСИОННОЕ УРАВНЕНИЕ с учётом коэффициента диффузии. Эти два приложения носят два названия:
1)где в глубине структуры -свободная граница, те границам потока ничем не ограничена, никак не ХАРАКТЕРИСТИКи не заданы, границам свободная. Так же как в прикладной механики, когда стержень не закреплён, свободный конец.
2)жёсткая граница-при жёсткой границе поток электронов его характеристики строго определены, из-за того, что есть граница, он распространяется рядом с ней. Поперечная составляющая невозможна. Аналогия, когда стержень закреплён.
ЖЁСТКАЯ ГРАНИЦА ДИСПЕРСИОННОЕ УРАВНЕНИЕ:
Это то же уравнение что и на первых слайдах ток поделенное на D. Беттар с чертой-нормированная беттар с учётом 1+дельта.
Решаем квадратное уравнение, следовательно, 2 решения.
Первая часть это постоянная нарастания альфа, вторая часть фазовая постоянная бета.
Рассмотрим фазовую постоянную для конкретной моды (н ой). Здесь знак +, это говорит о том, что ваша по-прежнему распространяется в прямом направлено.
Т.е. одна из волн которая возбуждается в такой структуре является прямой волной, при этом дробь стремится чаще всего к 0. За счёт того, что беттад она обычно имеет очень большое значение и если на него поделить произведение каппа на беттарн то получается очень маленькая величина и по сути фазовая постоянная для случая учёта ДИФФУЗИИ она все равно остаётся беттае.
Это говорит о том, что даже при условии учёта коэффициент диффузии скорость распространения волны все равно останется скоростью дрейфа электронов. (Скорость распространения волны не меняется при учете коэффициента диффузии).
А меняется величина амплитудной постоянной (альфа н пр). Помимо каппы на беттар появляется слагаемое беттае ^2/бетад. Чтобы происходили усиление произведение Кана на беттар должно быть отрицательным. А частная бета е квадрат на бета д положительная. Поэтому, когда суммируют то альфа

н начинает стремиться к 0. Те КОЭФФИЦИЕНТ усиления начинает так же стремится к 0. Более того если отношение беттае на бетад оказывается больше, чем каппа на беттар то альфа становится положительным и коэф усиления превращается в КОЭФФИЦИЕНТ ослабления.
Т.о. с учётом диффузии мы должны всегда помнить о том, что диффузия усиление уменьшает. Наличие ДИФФУЗИОННОго тока она узнает процесс усиления. Бетае пропорциональна частоте сигнала, который распространяется в П/П. С ростом частоты беттае растет соответственно и дробь становится больше, поэтому альфа становится (по сути, больше) все ближе к 0, поэтому ещё один вывод: с ростом частоты амплитудная постоянная будет стремиться к 0 и даже может стать положительной. Для любой моды 0,1,2,3 с ростом частоты ВЛИЯНИЕ ДИФФУЗИИ увеличивается. Потому что в амплитудной постоянной возникает дополнительная постоянная, которая все это дело объясняет. Спадание достаточно быстрое.
Если говорить о условиях жёсткой границе. Когда КОЭФФИЦИЕНТ диффузии для данного конкретного случая будет равен коэффициенту диффузии из справочника или измерен экспериментально, то мы можем наблюдать второе решение.
По сути, это вторая волна, которая может распространяться по такой структуре, которая возбуждается в любом случае (при возбуждении в принципе волн пространственного заряда ВОЗНИКАКТ знакперед фазовой постоянной, что говорить о том, что волна у нас обратная.
Т.е. если (на рисунке краснон) у нас стоит элемент возбуждения то, снизу появляется обеденная область и она начинает, с одной стороны, гнать волну прямую которая усиливается за счёт отрицательного значения капа на относительно низких частотах. И есть обратная волна она так же одновременно возбуждается. Обратная волна — это волна, у которой фазовая постоянная меняется, в одну сторону с прямой волной, а групповая скорость в другую или наоборот.
Будет распространяться обратная волна и она направлена, а сторону противоположную дрейфу электронов. Если для прямой волны электроны движутся в право (от истока к стоку), то для обратной волны дрейф электронов будет все туда же, а фаза меняться в другую сторону. При этом за счёт того, что величина бета д а в данном случае она является параметром Альфа, а бета е параметром бета (фазовая), за счёт большого значения бета д, она будет быстро-быстро затухать. По сути длинного распространения для обратной волны не возникает, она затухает.
Факт что здесь: альфа обр = - беттад , стоит минус не должен смущать потому что волна направляется в другую сторону. Если рассматривать как выглядит амплитуда волны обратной, это нарастающая слева направо экспонента, и тк волна в обратную сторону то и амплитуда должна рассматриваться в обратную сторону, как затухающий процесс.

Альтернативой является свободной границей
В случае свободной границы у нас есть распространение волны и существует как продольная, так и поперечная составляющие диффузионного тока. Сумма их определяется коэффициентом ДИФФУЗИИ D. То продольная составляющая, негативно влияющая на процесс распространения, уменьшается, соответственно при рассмотрении волнового процесса мы должны коэффициент ДИФФУЗИи сделать поменьше. По сути, использовать модифицированный КОЭФФИЦИЕНТ диффузии
Модифицированный КОЭФФИЦИЕНТ диффузии, в нем используется исходный коэф. диффузии который уменьшается в соответствии с геометрией структуры и коэффициентом анизотропии. Новое обозначение бетта д с чертой это то же беттад но делкнное на модиф. Коэф диффузии. (В0/д).
Уравнение выглядит более сложно, потому что мы должны использовать модиф коэф дифф. Но все равно уравнение по-прежнему квадратное.
Корня два и по-прежнему распространяется две волны, но в случае свободной границы одно из уравнений решения имеют сильно отличающийся вид. (Первый ответ такой же, как и при жесткой границе только беттад с чертой).
Это говорит о том, что одна из волн остаётся такой же прямой волной с такими же самыми характеристики, с одним лишь дополнением беттад становится другим. (Т.к. модиф коэф дифф это коэф лиф уменьшенный на величину соответственно и бетад увеличилось, раз так то немного уменьшилась дробь (бета е^2 на бетад с чертой)
, значит влияние ДИФФУЗИИ стало меньше. И с частотой ВЛИЯНИЕ не так сильно сказывается, особенно на низких частотах, на высоких не могу на то, что беттад немного меньше все равно ВЛИЯНИЕ оказывается уже очень сильное.
Поэтому про прямую волну тоже самое: она усиливается, влияет диффузия, влияет с частотой, направление прямо, скорость распространения волны (фазлвая) равна скорости дрейфа.
А вторая волна имеют форму отличную от жесткой границы.
Разница от первого ответа что мы здесь видим каппу, а там нет. Это говорит о том, что первая скобка (сумма слагаемых) — это альфа (амплитудная постоянная для данной волны, всегда больше нуля, просто
здесь нет отрицательного слагаемого. Т.е. амплитуда волны номер 2 (не путать со второй модой, это второй вид волны) она все время снижается. При этом рассматривая вторую часть уравнения, можно сказать, что она все равно прямая, скорость распространения очень близка к скорости дрейфа, но она затухающие.
По сути, не вносит влияния в процесс распространения волн в такой структуре.
АМПЛИТУДНОЧАСТОТНАЯ ХАРАКТЕРИСТИКА
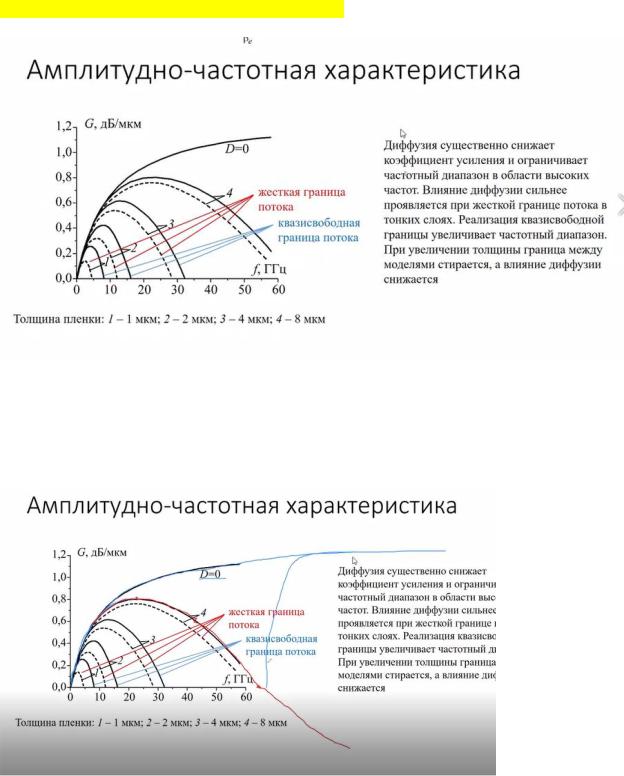
Это погонный Коэф. усиления, т.е. на единицу длины структуры {дБ/мкм} Верхняя линия показывает нулевое приближение. Для нее имеем нарастание и выход в насыщение. Если
мы говорим об учете влияния диффузии, то должны понимать, что у нас растет растет коэф усиления потом возникает максимум и с ростом частоты влияние ДИФФУЗИИ становится все сильнее и коэф усиления начинает снижаться. Можно достигнуть предельного значения, при котором кожф усиления равен 0, и при большИх частотах диффузия будет оказывать новодел более серьезное влияние чем процесс усиления, и мы не будем видеть никакого усиления будет только затухание.
Если сравнивать модели жёсткой и свободной границы потока то можно говорить, что даст модели жесткой границы в силу того что коэффициент ДИФФУЗИи весь работает на то чтобы погасить волну (снизить коэф усиления), то и во всем частотном диапазоне он будет ниже и ВЛИЯНИЕ его начнется чуть раньше на меньших частотах и амплитуда максимальная (Макс коэф усиления) во всем диапазоне ачх тоже будет меньше, только потому что коэф диффузии в данном процессе будет выше.
Из-за использования модифицированного коэф диффузии с меньшим значения для свободной (квазисвободной) границе потока будет меньше влияние ДИФФУЗИИ, больше коэффициент усиления. Если говорить о влиянии толщины пленки на процесс распространения волны.
Если мы говорим об очень тонкой пленке, то в этой пленке весь поток электронов будет распространяться вблизи границы те все электроны всего электронного потока (волны пространственного заряда), все будет двигаться в рамках модели жёсткой границы. Для них для всех КОЭФФИЦИЕНТ диффузии будет большим. И соответственно в тонкой пленке весь поток электронов, вся волна пространственного заряда работает в рамках модели жёсткой границы.
Если говорить о Толстой пленке, то даже если волна прижата к поверхности, то за счёт того, что поток электронов будет распределен в большЕм объеме пленки, в рамках модели свободной границы и жёсткой, двигаться будет разное количество электронов. Т.е. те, которые двигаются вблизи поверхности в рамках модели жёсткой границы, те кто движутся вдали от границы в рамках свободной границы. Резкого перехода между этими моделями нет. И чем толще пленка, тем больше электронов может двигаться в рамках свободной границы с меньшим коэффициентом усиления???наверно диффузии (тем выше коэф усиления).
Если говорить про тоненькую границу, из-за того, что очень малое число электронов может двигаться в такой структуре в рамках свободной границы, то и влияние самой модели (жёсткой или свободной) очень сильное. Потому что в тонких пленках, если мы берём модель жёсткой границы, то все электроны будут двигаться в рамках этой жёсткой границы, и мы не сможем выделить сколько-либо электронов чтобы они двигались в рамках свободной. Поэтому влияние модели очень сильное.
КАК МЫ МОЖЕМ УПРАВЛЯТЬ ГРАНИЦЕЙ ПОТОКА. (в рамках какой модели движется поток электронов)
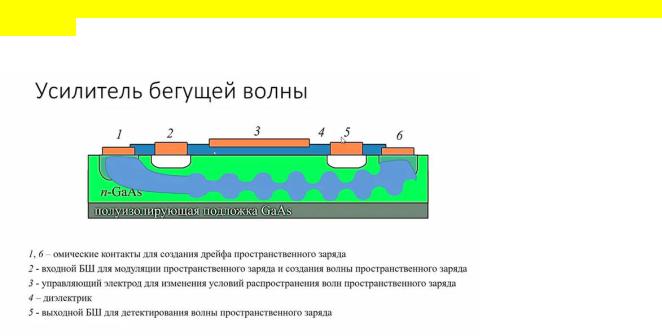
Сделать это можно при помощи 3го электрода
Помимо того, чтобы использовать толстую или тонкую пленку можем воспользоваться 3м электродом, который отделен от всей структуры диэлектрическим слоем. Т.е. он гальванически отвязан от потока электронов и даже если поток электронов двигался вдоль границы раздела П/П Д/Э электроны все равно нас управляющий электрод не попадали.
Если мы на такой затвор (упр электрод) начинаем подавать отрицательный потенциал, то он, как и в случае с мдп начинает создавать в этой области (под ним и Д/Э) дополнительный изгиб энергетических зон, он будет приводить к тому, что отрицательный потенциал будет загибать энергетическую диаграмму вверх и мы будем делать потенциальный барьер в области для электронов (там, где обедненная). Таким образом электроны будут этим потенциальным барьером отжиматься (отталкиваться) от Д/Э слоя, от управляющего электрода вглубь пленки. т.о. граница потока электронов (полная ПРОСТРАНСТВЕННОГО заряда) будет отделена от границы раздела Дэ ПП (в область п/п -п/п). И мы сможем говорить, что модель распространения свободная. Если мы подаем положительный потенциал, то мы, наоборот, можем притянуть электроны. Создав не потенциальный барьер, а потенциальную яму и электронная, приблизившись будут делаться, а рамках модели жёсткой границы. т.о. можем наблюдать способ электронного управления коэф. усиления такого усилителя, при этом расчетные и экспериментальные измерения показали, что такой усилитель может давать коэф усиления до 30дб, это неплохо.
