
Практика 1 - Сортировки массивов - СФ
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕЕНЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
Сортировка массивов Отчет по практической работе №1
По дисциплине «Структуры данных»
Студент гр. ххххх
________ ххххх
________
Принял Преподаватель КИБЭВС
________ ххххх
________
Томск 2022
Содержание
1 Введение ……………………………………………………………………….. 3
2 Ход работы …………………………………………………………………….. 4
2.1Сортировка «расческой» ……………………………………………… 4
2.2Быстрая сортировка ………………………...…………………………. 6
2.3Сортировка Шелла ...………………………………………………….. 6 3 Алгоритмическая сложность ………………………………………………..… 8
Заключение ………………………………………………………………………. 9
Приложение А ………………………………………………………………..… 10
Приложение Б …………………………………………………………………... 11
Приложение В …………………………………………………………………... 13
2
1 Введение
Целью данной практической работы является получение навыка работы с сортировками. Будут изучены сортировка «расческой», быстрая сортировка и сортировка Шелла. Для разработки сортировок будет использован язык программирования C#.
3

2 Ход работы
Будет реализовано 3 сортировки: сортировка «расческой», быстрая сортировка и сортировка Шелла. Также дополнительным условием варианта было то, что входные данные представлены только числами двоичной точности с плавающей точкой.
2.1 Сортировка «расческой»
Сортировка «расческой» является усовершенствованным вариантом сортировки «пузырьком». Идея этой сортировки заключается в том, что элементы будут сравниваться через определенный шаг. Шаг будет постепенно уменьшаться, благодаря фактору уменьшения. Он высчитывается по формуле
2.1 и равен 1.247:
1 |
= 1,247 |
(2.1) |
1−− |
где – золотое сечение или золотое число;
е – экспонента, равна 2.718.
На последней итерации цикла шаг будет равен одному и это эквивалентно одному проходу сортировки пузырьком.
На рисунке 2.1 представлена блок-схема данной сортировки, на рисунке
2.2 представлена работа конструкции Try-Catch - это конструкция обрабатывает вводимые данные и если они не верны, то выводит предупреждение на экран. Эта конструкция реализована во всех последующих алгоритмах. И также на рисунке 2.3 представлен результат работы программы.
В приложении А представлен листинг программы сортировки
«расческой».
4
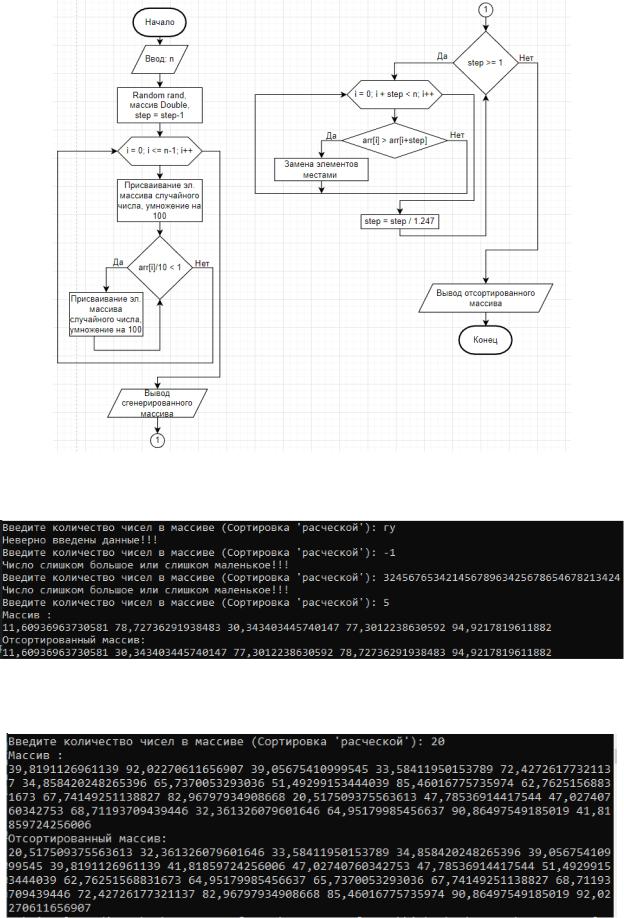
Рисунок 2.1 - Блок-схема сортировки
Рисунок 2.2 - Работа конструкции Try-Catch
Рисунок 2.3 - Результат работы программы
5

2.2 Быстрая сортировка
Общая идея этой сортировки заключается в том, чтобы разделить входной набор данных относительно опорного элемента. Все элементы,
которые меньше опорного перемещаются в нижнюю часть массива, большие остаются на своих местах. В результате выполнения этих действий весь массив должен разделиться на три группы, следующие друг за другом: меньше опорного, равная опорному и больше опорного. Для «больших» и «меньших» отрезков рекурсивно выполняется та же последовательность действий.
Опорный элемент выбирается на каждой итерации. Сортировка реализована рекурсией.
Реализация алгоритма быстрой сортировки была осуществлена с помощью рекурсии, опорный элемент выбирался на каждой итерации по методу разбиения Хоара, где берется сумма первого элемента последовательности и последнего, и делится на два.
На рисунке 2.4 представлен результат работы программы.
Рисунок 2.4 - Результат работы быстрой сортировки В приложении Б представлен листинг программы быстрой сортировки.
2.3 Сортировка Шелла
Является усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и
6
на определённом расстоянии друг от друга. Элементы сравниваются через определенный шаг.
На первой итерации шаг равен половине длины массива, т.е.
сравниваются первый и последний элементы массива. Затем шаг уменьшается в два раза, пока не станет равным нулю. Когда шаг будет равен единице, это будет эквивалентно одному проходу сортировки вставками.
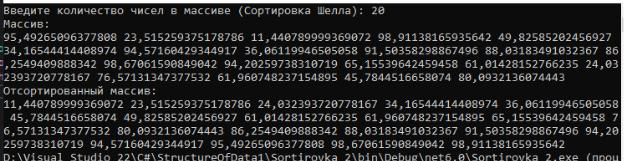
На рисунке 2.5 представлен результат работы программы.
Рисунок 2.5 - Результат работы сортировки Шелла В приложении В представлен листинг программы сортировки Шелла.
7
3 Алгоритмическая сложность
Все три сортировки в худшем случае имеют O(n^2). Но в лучшем случае быстрая сортировка и сортировка «расческой» имеют одинаковую временную сложность, она равна O(n log n), но сортировка Шелла в лучшем случае имеет временную сложность O (N lg N) соответственно, также она неустойчива к одинаковым элементам. Следовательно сортировка Шелла – самая худшая из трех представленных сортировок.
8
Заключение
В ходе выполнения данной практической работы были получены навыки разработки алгоритмов сортировки на языке программирования C#. Были изучены алгоритм сортировки «расческой», алгоритм быстрой сортировки, а
также алгоритм сортировки Шелла.
Наиболее затруднительным был алгоритм быстрой сортировки.
9
Приложение А
(обязательное)
Сортировка «расческой»
using System;
namespace StructureOfData1
{
class Program
{
static void Main(string[] args)
{
try
{
Console.Write("Введите количество чисел в массиве (Сортировка 'расческой'): ");
int n = int.Parse(Console.ReadLine()); Random rand = new Random();
double[] arr = new double[n]; for (int i = 0; i <= n-1; i++)
{
arr[i] = rand.NextDouble(); arr[i] *= 100;
while (arr[i] / 10 < 1)
{
arr[i] = rand.NextDouble(); arr[i] *= 100;
}
}
Console.WriteLine("Массив : ");
foreach (double d in arr) Console.Write(d + " "); int step = n - 1;
while (step >= 1)
{
for (int i = 0; i + step < n ; i++)
{
if (arr[i] > arr[i + step])
{
double temp = arr[i]; arr[i] = arr[i + step]; arr[i + step] = temp;
}
}
step = Convert.ToInt32(Math.Floor(step / 1.247));
}
Console.WriteLine(); Console.WriteLine("Отсортированный массив: "); foreach (double d in arr) Console.Write(d + " ");
}
catch (System.FormatException)
{
Console.WriteLine("Неверно введены данные!!!"); Main(args);
}
catch (System.OverflowException)
{
Console.WriteLine("Число слишком большое или слишком маленькое!!!"); Main(args);
}
}
}
}
10
