Лаба 3 - Интерполяция и аппроксимация - СФ

1 Введение

Цель работы: получить навыки вычисления интерполяционного полинома Лагранжа и аппроксимирующей функции.

2

2 Ход работы

2.1 Вычисление точек

Необходимо вычислить 14 точек с координатами (xi , yi). xi = 0, 2 i

i = 0, 13 yi = f(xi)

f(xi) – индивидуальная функция.

Индивидуальная функция изображена на рисунке 2.1.

Рисунок 2.1 - Индивидуальная функция

На рисунке 2.2 показано, какие точки были получены.

Рисунок 2.2 - Полученные точки

3

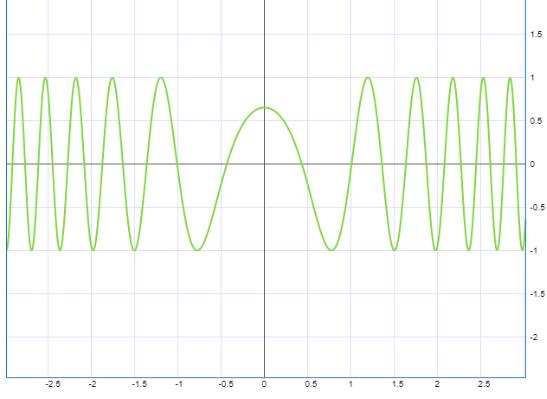
На рисунке 2.3 показана построенная индивидуальная функция.

Рисунок 2.3 - Индивидуальная функция

2.2 Вычисление полинома Лагранжа

Интерполяционный полином Лагранжа в коде реализует метод Lagrange.

На вход подаются введенный x, индексы точек, которые находятся рядом с введенным х, они определяются методом Findindex, в котором введенная точка сравнивается с х, и находятся 1 индекс слева от точки и 2 индекса справа, если это точка не попадает в интервал от 12 до 13 точек, в таком случае берутся 2

точки слева и 1 справа, т.е. 13 точка.

Далее вычисляется полином Лагранжа второй степени, т.к. выбранных точек 3. Вместе с полиномом Лагранжа на экран выводится и индивидуальная функция, которая считается методом Function. На рисунке 2.4 приведен пример показаний полинома Лагранжа и индивидуальной функции, и как видно они совпадают, что и должно происходить согласно определению полинома Лагранжа.

4

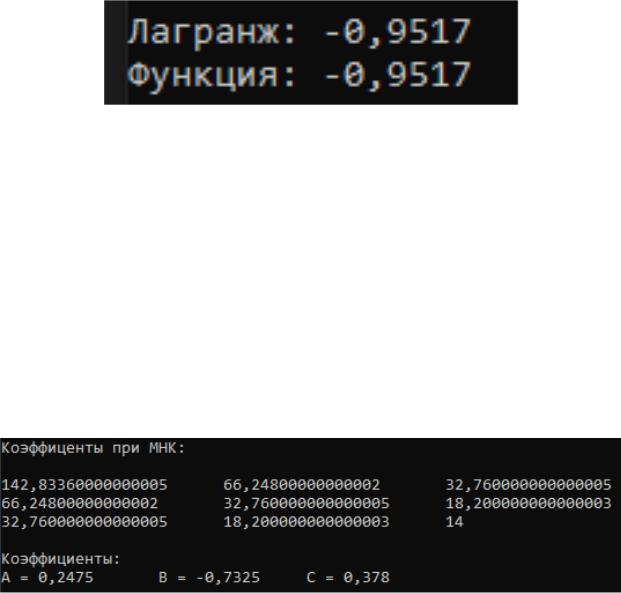
Рисунок 2.4 - Проверка корректности полинома Лагранжа

2.3 Аппроксимация и метод наименьших квадратов(МНК)

Для аппроксимации использовалась квадратичная функция ax2+bx+c, в

которой неизвестны коэффициенты a,b,c. Они были найдены с помощью МНК.

Реализация МНК осуществляется в методе MinQuadro, в котором вычисляются ∑x4,∑x3,∑x2,∑y*x2,∑x,∑y,∑x*y. Для нахождения a,b,c, т.е.

неизвестных коэффициентов в квадратном уравнении, был использован метод Зейделя. На рисунке 2.5 приведены найденные коэффициенты.

Рисунок 2.5 - Коэффициенты для МНК

На рисунке 2.6 представлены точки полученной аппроксимирующей точки.

5

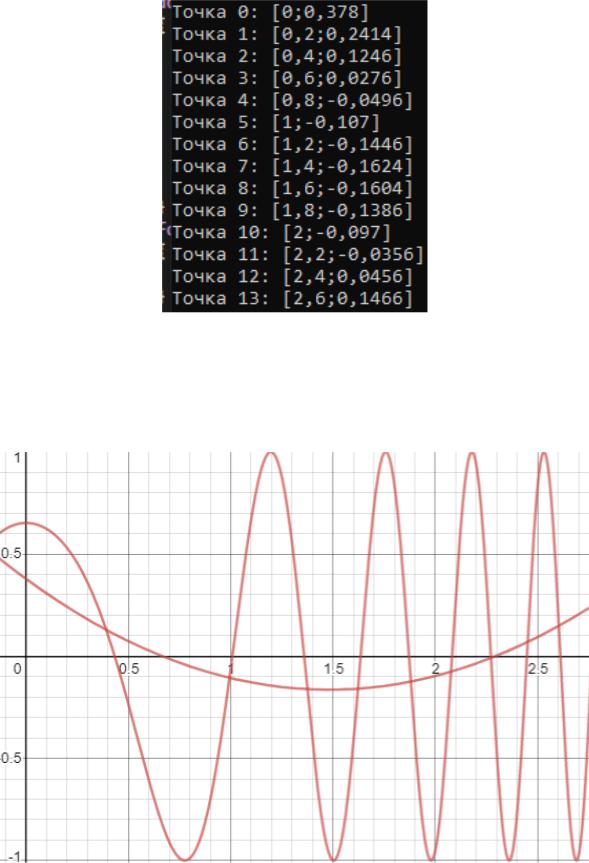
Рисунок 2.6 - Точки при аппроксимации

На рисунке 2.7 представлен совместный график аппроксимирующей и индивидуальной функций.

Рисунок 2.7 - Совместный график индивидуальной и аппроксимирующей функций

6

В таблице 1 указаны значения х для индивидуальной, аппроксимирующей

функций, а также для полинома Лагранжа.

Таблица 1 – Сводная таблица

7

3Заключение

Входе выполнения данной лабораторной работы были получены навыки вычисления интерполяционного полинома Лагранжа и аппроксимирующей функции.

Листинг программы представлен в приложении А.

8

Приложение А

(обязательное)

using System; namespace m43

{

class Program

{

static void Findindex(double[] X, double x,ref int zLeft,ref int z, ref int

zRight)

{

for (int i = 0; i < 14; i++)

{

if (x == 0) break;

if (X[i] < x) zLeft = i; if (X[i] == x)

z = i;

if (X[i] > x)

{

zRight = i; break;

}

}

if (zRight == 13)

{

zLeft = 11; z = 12; zRight = 13;

}

if (zLeft == 13)

{

zLeft = 11; z = 12; zRight = 13;

}

if (z == 0)

{

z = zRight; zRight++;

}

}

static double Function(double X)

{

double F = Math.Cos(3.79 * Math.Pow(X, 2) + 0.86); return F;

}

static void MinQuadro(double[] X,double[] Y,ref double[,] A, ref double[] B, ref double[] XMinQ)

{

B[1] += X[i] * Y[i]; B[2] += Y[i];

}

A[2, 2] = 14;

double Eps = 0.000000000001; do

{

for (int i = 0; i < 3; i++)

{

XPast[i] = XMinQ[i];

}

XMinQ[0] = B[0] / A[0, 0] - (XPast[1] * A[0, 1]) / A[0, 0] - (XPast[2] * A[0,2]) / A[0, 0];

XMinQ[1] = B[1] / A[1, 1] - (XMinQ[0] * A[1, 0]) / A[1, 1] - (XPast[2] *A[1, 2] / A[1, 1]);

XMinQ[2] = B[2] / A[2, 2] - (XMinQ[0] * A[2, 0]) / A[2, 2] - (XMinQ[1] *A[2, 1]) / A[2, 2];

} while (Math.Abs(XMinQ[0] - XPast[0]) >= Eps || Math.Abs(XMinQ[1] - XPast[1]) >= Eps || Math.Abs(XMinQ[2] - XPast[2]) >= Eps);

for (int i = 0; i < 3; i++)

{

XMinQ[i] = Math.Round(XMinQ[i], 4);

}

}

static void Lagrange(double[] X, double[] Y,double x,int zLeft, int z, int zRight, double[] XMinQ)

{

if (zLeft == 0 && zRight == 0)

{

Console.WriteLine("С нуля начинается исследование"); Console.Write("X для Лагранжа: ");

double index = Convert.ToDouble(Console.ReadLine()); Lagrange(X, Y, index, zLeft, z, zRight, XMinQ);

}

else

{

double l1 = (x - X[z]) / (X[zLeft] - X[z]) * (x - X[zRight]) / (X[zLeft] - X[zRight]);

double l2 = (x - X[zLeft]) / (X[z] - X[zLeft]) * (x - X[zRight]) / (X[z] - X[zRight]);

double l3 = (x - X[z]) / (X[zRight] - X[z]) * (x - X[zLeft]) / (X[zRight] - X[zLeft]);

double L = l1 * Y[zLeft] + l2 * Y[z] + l3 * Y[zRight]; Console.WriteLine($"Лагранж: {Math.Round(L, 4)}"); Console.WriteLine($"Функция: {Math.Round(Function(x),4)}"); double Appr = XMinQ[0] * Math.Pow(x, 2) + XMinQ[1] * x + XMinQ[2]; Console.WriteLine($"Аппроксимация: {Math.Round(Appr,4)}");

}

}

static void Main(string[] args)

{

double[] Approx = new double[14];

double[,] Arr = { { 0, 0, 0 }, { 0, 0, 0 }, { 0, 0, 0 } }; double[] B = {0,0,0};

double[] XMinQ = { 0, 0, 0 };

double[] X = new double[14]; double[] Y = new double[14]; int zRight = 0; int zLeft = 0; int z = 0;

for (int i = 0; i < 14; i++)

{

X[i] = 0.2 * i;

Y[i] = Function(X[i]);

Console.WriteLine($"Точка {i}: [{Math.Round(X[i], 3)};{Math.Round(Y[i],4)}]");

}

Console.Write("\nХ для Лагранжа: ");

10