
Лаба 2 - Численное решение нелинейных уравнений с одной переменной - СФ
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕЕНЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
Численное решение нелинейного уравнения с одной переменной Отчет по лабораторной работе №2
По дисциплине «Численные методы»
Студент гр. Ххх-хх
________ Х. Х. Хххх
________
Принял Старший преподаватель КИБЭВС
________ Х. Х. Хххх
________
Томск 2022
1 Введение
Цель работы: получить навыки решения нелинейного уравнения с одной переменной методом ньютона, простых итераций и методом дихотомии.
Для тестирования использовать систему уравнений:
X2 + 4x − 5 = 0
Решения: x1 = −5; x2 = 1.
Начальная точка при всех тестированиях равна половине отрезка, а отрезок задан, так что X [-2;2].
2
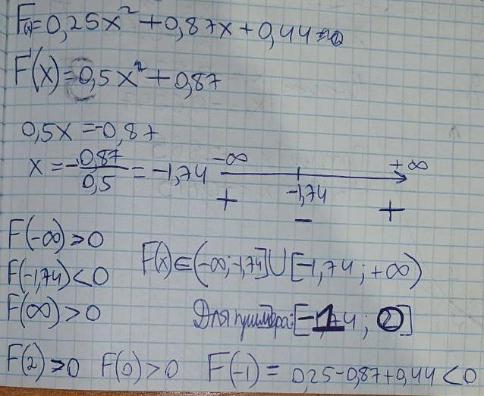
2 Ход работы
2.1 Этап отделения корня
Отделение корня – это первый шаг, который необходим для нахождения границы, в которой функция монотонная и имеет один корень, т.е. пересекает ось X ровно один раз.
Нахождение начального отрезка было выполнено вручную и представлено на рисунке 2.1. Отрезок был выбран X[-1;0].
Рисунок 2.1 - Преобразование функции
Функция индивидуального уравнения представлена на рисунке 2.2
3
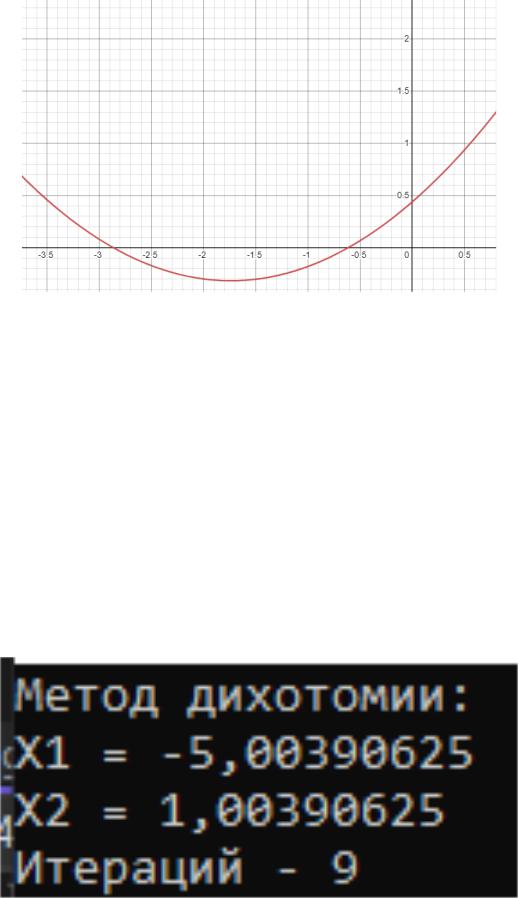
Рисунок 2.2 - График индивидульной функции
2.2Нахождение корня методом дихотомии
Вданном методе отрезок делится пополам и в ищется функция от точки на середине данного отрезка, если функция имеет такой же знак как правая точка,
то средина становится правой границей, если же как левая точка, то левой границей. Так продолжается до тех пор пока модуль разности X на предыдущей операции не станет меньше условия остановы. На рисунке 2.3 приведено тестирование функции, а на рисунке 2.4 приведено решение индивидуальной функции.
Рисунок 2.3 - Тестирование функции
4
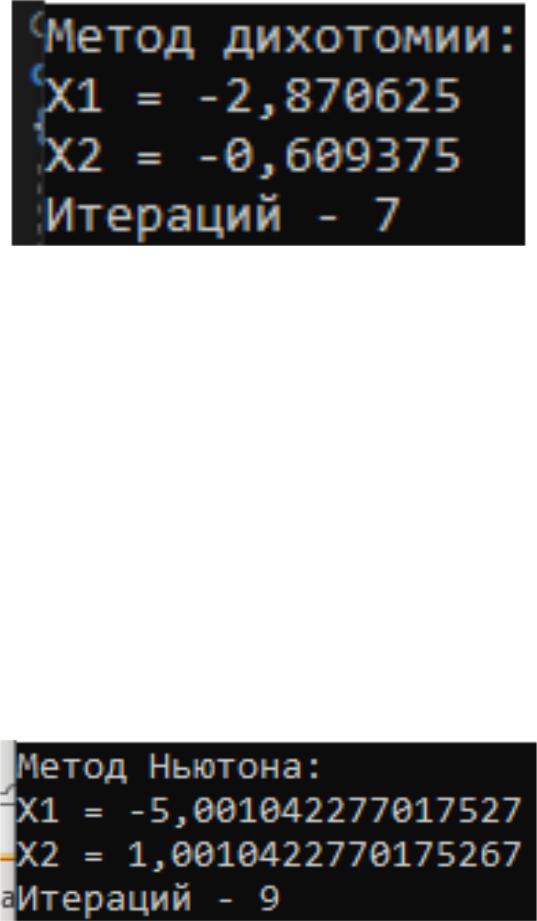
Рисунок 2.4 - Решение индивидульной функции
Листинг программы приведен в приложении А.
2.3Нахождение корня методом Ньютона
Вданном методе сначала проводят касательную к функции в отрезке,
выбранном пользователем, затем находится точка пересечения касательной с осью OX и эта точка будет первым приближением для искомого корня. Затем каждому последующему X присваивается разница между X на предыдущей итерации и делением функции от предыдущего X на первую производную.
Условие остановы определятся значением функции от X на текущей итерации,
если оно меньше E, которое равно 0.01.
На рисунке 2.5 представлено тестирование метода Ньютона, а на рисунке
2.6 решение индивидуальной функции.
Рисунок 2.5 - Тестирование методом Ньютона
5
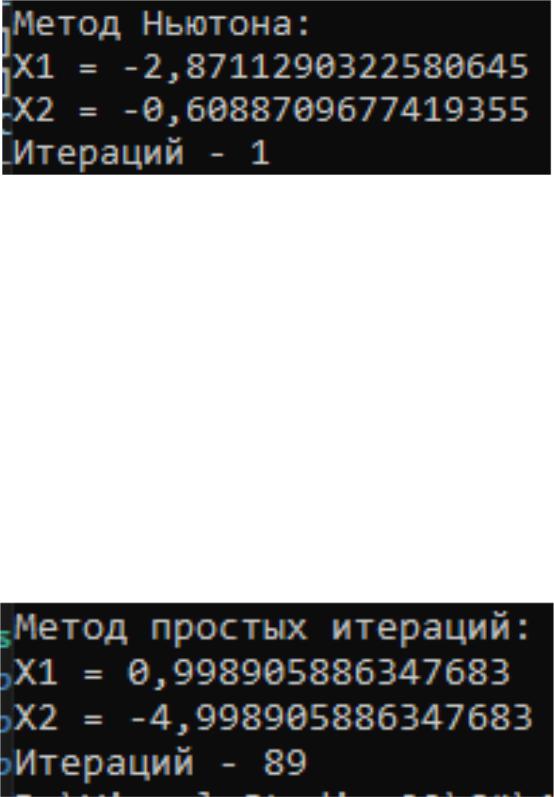
Рисунок 2.6 - Решение функции методом Ньютона
Листинг программы приведен в приложении Б.
2.4Нахождение корня методом простых итераций
Вданном методе X присваивается сумма X, на предыдущей итерации, и
произведения функции X, на предыдущей итерации и L, которое равно -2
деленому на первую производную от функции, X на прошлой итерации.
Программа останавливается, тогда когда модуль разности X будет меньше заданной точности.
На рисунке 2.7 представлено тестирование методом простых итерации, а
на рисунке 2.8 решение индивидуальной функции.
Рисунок 2.7 - Тестирование методом простых итераций
6
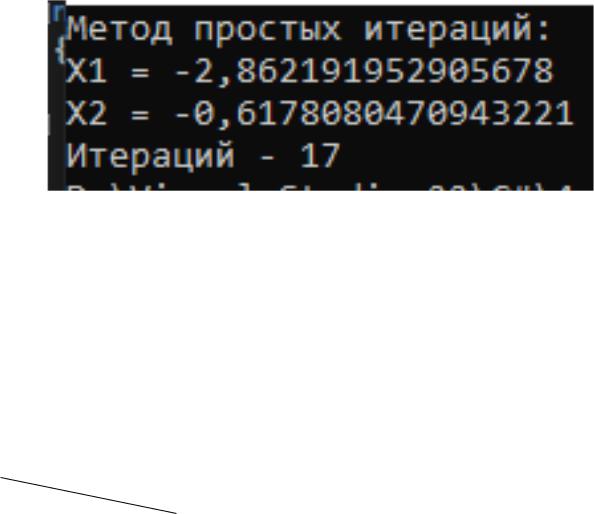
Рисунок 2.8 - Решение методом простых итераций
Листинг программы представлен в приложении В.
2.5Сравнительная таблица
Втаблице 1 показано сравнение методов решения нелинейных уравнений
содной переменной.
Таблица 1 – Сравнительная таблица методов
Результаты |
Начальная точка |
Число итераций |
Найденный корень |
Метод |
|
|
|
Метод дихотомии |
-0.5 |
7 |
-0.6094 |
Метод Ньютона |
-0.5 |
1 |
-0.6089 |
Метод простых |
-0.5 |
17 |
-0.6178 |
итераций |
|
|
|
7
3Заключение
Входе выполнения данной лабораторной работы были получены навыки решения нелинейного уравнения с одной переменной методом ньютона, простых итераций и методом дихотомии.
8
Приложение А
(обязательное)
Метод дихотомии
using System; namespace m4_2
{
class Program
{
static void Main(string[] args)
{
Console.WriteLine("Метод дихотомии:"); double[] X = new double[3];
double[] A = { 0.25, 0.87, 0.44 }; double CentreFun = -1.74;
X[0] = -1;
X[1] = 0;
X[2] = (X[0] + X[1]) / 2; double eps = 0.01;
int iteration = 0;
while (Math.Abs(X[1] - X[0]) >= eps )
{
double F = A[0] * X[2] * X[2] + A[1] * X[2] + A[2]; if (F > 0)
{
X[1] = X[2];
X[2] = (X[0] + X[1]) / 2;
}
if (F <= 0)
{
X[0] = X[2];
X[2] = (X[0] + X[1]) / 2;
}
iteration++;
}
X[0] = (CentreFun - X[1]) * 2 + X[1];
Console.Write($"X1 = {X[0]}" + "\n" + $"X2 = {X[1]}" + "\n" + $"Итераций - {iteration}");
}
}
}
9
Приложение Б
(обязательное)
Метод Ньютона
using System; namespace Nuton
{
class Program
{
static void Main(string[] args)
{
Console.WriteLine("Метод Ньютона:"); double F = 0;
double[] X = new double[3]; double[] A = { 0.25, 0.87, 0.44 }; double CentreFun = -1.74;
X[0] = -1;
X[1] = 0;
X[2] = (X[0] + X[1]) / 2;
double FSHT = 0.5 * X[2] + 0.87; double eps = 0.01;
int iteration = 0; do
{
F = A[0] * X[2] * X[2] + A[1] * X[2] + A[2]; X[2] = X[2] - F / FSHT;
iteration++;
} while (Math.Abs(A[0] * X[2] * X[2] + A[1] * X[2] + A[2]) >= eps); X[0] = (CentreFun - X[2]) * 2 + X[2];
Console.Write($"X1 = {X[0]}" + "\n" + $"X2 = {X[2]}" + "\n" + $"Итераций - {iteration}");
}
}
}
10
