3.2. Общие свойства обратимых и необратимых циклов

Термический КПД цикла Карно определяется из выражения (3.1) или (3.2), то есть в цикле Карно

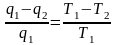или ; ; .

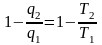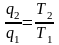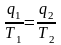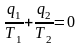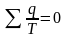В соответствии с принятым правилом знаков величина теплоты q₁, подводимой к рабочему телу, считается положительной, а теплоты q₂, отводимой от рабочего тела, считается отрицательной. Значит, последнее соотношение можно записать в форме или (3.4)

Из выражения (3.4) следует: в обратимом цикле Карно алгебраическая сумма приведенных теплот равна нулю. Рассмотрим произвольный обратимый цикл 1-2-3-4 (рис. 3.7).

Разобьем его с помощью адиабат на бесконечное множество элементарных циклов. Каждый из этих циклов образуется двумя адиабатами и двумя элементарными участками основного цикла, которые можно рассматривать как изотермы подвода и отвода теплоты.

Разобьем его с помощью адиабат на бесконечное множество элементарных циклов. Каждый из этих циклов образуется двумя адиабатами и двумя элементарными участками основного цикла, которые можно рассматривать как изотермы подвода и отвода теплоты. Таким образом, каждый элементарный цикл является элементарным циклом Карно, для которого в соответствии с выражением (3.4) можно записать:

.

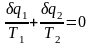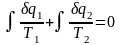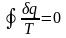Интегрируя это выражение по верхней ветви подвода теплоты и по нижней ветви отвода теплоты, получим или, по аналогии с выражением (3.4) можно записать интегральную сумму и заменить последнее равенство на круговой интеграл: (3.5)

В выражениях (3.4) и (3.5) температуры рабочего тела равны температурам источников теплоты, так как мы имеем дело с обратимыми процессами. Количество теплоты, отбираемой от источника, равно количеству теплоты, передаваемой рабочему телу, но знак δq берется относительно рабочего тела, то есть подведенная к рабочему телу теплота  положительная, отведенная от рабочего тела – отрицательная.

Интеграл (3.5) называется первым интегралом Клаузиуса, и его можно рассматривать как математическое выражение Второго закона термодинамики для обратимых циклов, так как отправным пунктом его доказательства является Второй закон термодинамики. Интеграл (3.5) показывает, что для превращения теплоты в работу нужно иметь горячие (δq>0) и холодные (δq<0) источники теплоты, иначе 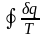не будет равен нулю.

Рассмортим необратимые циклы.

Термический КПД обратимого цикла Карно

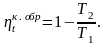
В этом выражении температура горячего источника Т₁ в процессе подвода теплоты равна температуре рабочего тела Т₁, температура холодного источника Т₂ равна температуре рабочего тела Т₂ в процессе отвода теплоты (это условие обратимости процессов).

В необратимом цикле Карно Т₁ > Т₁, а Т₂ < Т₂. Поэтому процессы подвода и отвода теплоты, а значит, и весь цикл, являются необратимыми. Необратимость вызвана отсутствием температурного равновесия между рабочим телом и источниками теплоты. КПД необратимого цикла Карно

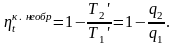
меньше термического КПД обратимого цикла Карно, осуществляемого в том же интервале температур:  .

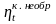
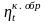Учитывая, что q₂  теплота отводимая, получим

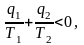(3.6)

где Т₁ и Т₂  температуры теплоотдатчика и теплоприемника; они не равны температурам рабочего тела при подводе и отводе теплоты. Неравенство (3.6) показывает, что в необратимом цикле Карно алгебраическая сумма приведенных теплот меньше нуля.

Как и в предыдущем случае, обобщим полученное неравенство на произвольный необратимый цикл. Для этого необратимый цикл с помощью адиабат разобьем на бесконечное множество элементарных необратимых циклов Карно. Для каждого из этих элементарных циклов можно применить неравенство (3.6) в виде

,

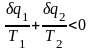После интегрирования по участкам подвода и отвода теплоты получим

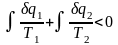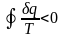, или (3.7)

В этом неравенстве, как и в неравенстве (3.6), температура относится не к рабочему телу, а к теплоотдатчикам и теплоприемникам, и знак q берется относительно рабочего тела. Неравенство (3.7) называется вторым интегралом Клаузиуса, и его можно рассматривать как математическое выражение второго закона термодинамики для необратимых циклов.

Объединяя формулы (3.5) и (3.7), получим неравенство

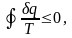(3.8)

называемое аналитическим выражением II закона термодинамики. Знак равенства относится к обратимым, а знак неравенства – к необратимым циклам.