
03 Определение удельной теплоты кристаллизации олова
.pdfЛАБОРАТОРНАЯ РАБОТА
Определение удельной теплоты кристаллизации
Цель работы: Определить удельную теплоту кристаллизации оловянного сплава и изменение энтропии в процессе его кристаллизации.
Приборы и оборудование: Лабораторная установка для плавления образца и измерения его температуры в процессе охлаждения.
Краткая теория.
Кристаллизацией называется процесс перехода вещества из жидкого состояния в твердое. Он относится к фазовым переходам первого рода и для химически чистых веществ сопровождается выделением теплоты при постоянной температуре. Температура кристаллизации для таких веществ равна температуре их плавления.
Количество теплоты, которое необходимо отвести от единицы массы жидкости при температуре кристаллизации для перехода жидкости в твердое состояние называется удельной теплотой кристаллизации Qкр. Первое начало термодинамики для данного процесса можно записать в виде:
Qкр=Uтв - Uж +р(Vтв - Vж) |
(1) |
Здесь Uтв и Uж - внутренние энергии единицы массы в твердом и жидком состояниях соответственно. Vтв и Vж – удельные объемы твердой и жидкой фазы; р – давление в процессе кристаллизации.
Поскольку при переходе из жидкого в твердое состояние удельные объемы металлических веществ изменяется незначительно, то:
|
р(Vтв - Vж) << Uтв - Uж |
|
Тогда: |
Qкр=Uтв - Uж |
(2) |
Энтропия – функция состояния термодинамической системы. Ее изменение в равновесном процессе равно отношению количества теплоты, сообщенной системе, к температуре, при которой она была передана.
dS |
Q |
(3) |
|
T |
|
Здесь δQ – элементарное количество теплоты полученное или отданное системой при бесконечно малом изменении ее параметров, когда Т можно считать неизменной.
Энтропия определяется с точностью до постоянной, но неопределенность в абсолютном значении энтропии в данном случае не важна, так как будет определяться ее изменение в процессе, т.е. разность энтропии конечного состояния и начального.
|
2 |
Q |
|
S2 S1 |
|
T |
(4) |
|
|
||
|
1 |
|
|
Описание установки и вывод расчетных формул.
Общий вид лабораторной установки для выполнения работы приведен на рис.1. В корпусе установки находится электрическая печь (не видна) и все электрические коммуникации. На переднюю панель корпуса выведен индикатор 1, высвечивающий температуру исследуемого образца, тумблер 7 включения нагрева печи и тумблер 8 – включения термометрической схемы. На корпусе укреплен защитный кожух, в котором располагается шток 2, по которому с помощью ручки 3 поднимается или опускается ампула 5 с исследуемым образцом.
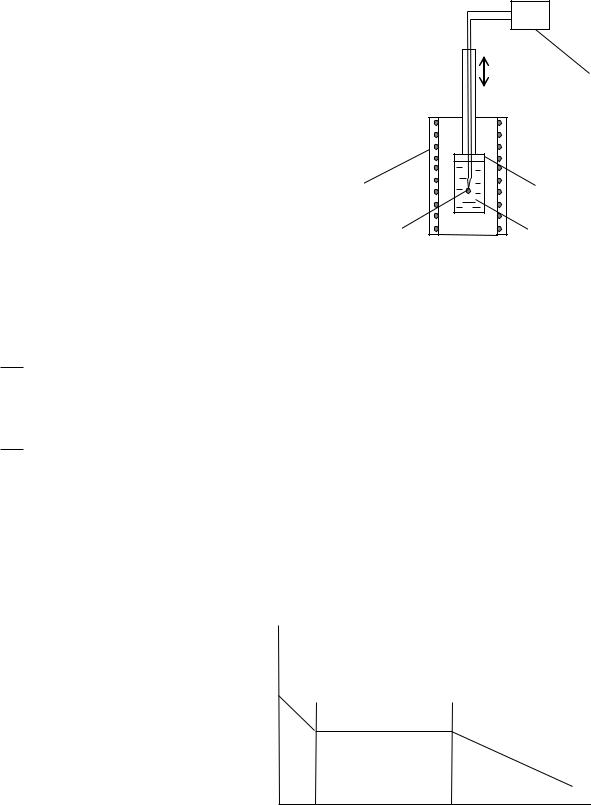
|
Принципиальная схема установки показана на рис.2. Исследуемый образец 1, в каче- |
|||||||
стве которого в установке используется сплав на основе олова, помещен в ампулу 2. Ам- |
||||||||
пула может вертикально перемещаться по штоку, который показан на рис.1. В нижнем |
||||||||
положении |
ампула размещается в печи 3, |
|
|
|
Т |
|||
нагревается до расплавления образца, а затем |
|
|
|
|||||
|
|
|
|
|||||
поднимается в верхнее положение, в котором |
|
|
|
|
||||
происходит |
охлаждение |
и |
кристаллизация |
|
|
|
5 |
|
сплава. Температура образца измеряется тер- |
|
|
|
|||||
|
|
|
|
|||||
мопарой 4 и высвечивается на индикаторе 5 в |
|
|
|
|
||||
градусах Цельсия. |
|
|
|
|
|
|
||
|
Простейшей моделью охлаждения нагре- |
|
|
|
|
|||
того тела является охлаждение в среде с посто- |
|
|
|
|
||||
янной температурой (в |
термостате) Тср. Эта |
3 |
|
|
2 |
|||
модель близка к реальному процессу охлажде- |
|
|
||||||
|
|
|
|
|||||
ния ампулы на воздухе комнатной температу- |
|
|
|
|
||||
ры. Поскольку процесс охлаждения происхо- |
4 |
|
|
1 |
||||
дит достаточно медленно, можно считать, что |
|
|
||||||
|
|
|
|
|||||
температура по объему образца одинакова в |
|
|
Рис. 2 |
|||||
любой точке. Т.е. реальный процесс охлажде- |
|
|
||||||
|
|
|
|
|||||
ния близок к квазистатическому, который по определению является обратимым. |
||||||||
|
В таких условиях можно предположить, что скорость выделения теплоты кристалли- |
|||||||
зации равна скорости теплоотдачи в окружающую среду. |
|
|
|
|||||
m |
Q , где t - продолжительность кристаллизации, m – масса образца, λ – удельная |
|||||||
t |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
теплота кристаллизации. |
Обозначив скорость |
теплоотдачи |
t |
Q |
можно записать: |
|||
m |
|
|
|
|
|
|
|
|
t |
Q , откуда определяется искомая величина: |
|
|
|
|
|||
|
|
|
|
t |
|
|
|
|
|
|
|
|
Q m |
(5). |
|
|
|
Т.к. в процессе кристаллизации температура образца не меняется, то скорость теплоотдачи в этот период не может быть измерена непосредственно. Оценить ее можно следующим образом. Поскольку скорость теплоотдачи при прочих равных условиях зависит только от разности температур нагретого тела и охлаждающей среды, определим ее до начала кристаллизации и после нее. Среднее значение полученных двух величин можно считать скоростью теплоотдачи в процессе кристаллизации. На рис. 3 в общем виде показан график изменения температуры
образца в процессе охлаждения. Про- |
Т,K |
|
|
|
|
|||||
цесс кристаллизации происходит с |
|
|
|
|
|
|||||
момента t1 до момента t2. |
|
|
|
|
|
|
||||
|
t2 - t1 = |
t |
|
|
|
|
|
|
||
Скорость изменения температуры, или |
|
|
|
|
|
|||||
скорость охлаждения |
на участках 1 |
|
|
|
|
|
||||
(охлаждение жидкой фазы) и 3 (охла- |
1 |
|
|
|
|
|||||
2 |
|
3 |
|
|||||||
ждение твердой фазы), определяется |
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
||||||
по наклону соответствующих прямых, |
|
|
|
|
|
|||||
как |
( T ) |
1 |
и |
(T ) 3 |
соответ- |
t1 |
|
t2 |
|
t,c |
( t ) |
|
|
|
|||||||
1 |
( t) 3 |
|
|
Рис.3 |
|
|
||||
|
|
|
|
|
|
|
||||
ственно.
Скорость теплоотдачи образца в процессе кристаллизации определяется по формуле:
|
(MC |
|
mC ) |
(T ) 1 |
(MC |
|
mC ) |
(T ) 3 |
|
|
|
||
|
|
|
|
|
|||||||||
|
M |
m (t) 1 |
M |
|
m |
(t) 3 |
|
||||||
Q |
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Где m и M - масса образца и ампулы соответственно; |
С |
и C |
- удельные теплоемко- |
||||||||||
|
|
|
|
|
|
|
|
m |
m |
|
|||
сти жидкого и твердого олова; CM - удельная теплоемкость материала ампулы.
Зная m, Δt и Q , по формуле 5 вычисляется удельная теплота кристаллизации, которая равна удельной теплоте плавления.
Изменение энтропии образца в процессе его охлаждения можно определить, основываясь на свойстве аддитивности энтропии. Поскольку образец остывает, т.е. отдает тепло в окружающую среду и в нем появляется упорядоченность в расположении атомов, энтропия должна убывать. Ее уменьшение можно представить в виде трех слагаемых:
S1 – уменьшение энтропии при остывании жидкого олова; S2 – уменьшение энтропии при кристаллизации олова;
S3 – уменьшение энтропии при остывании твердого олова. Общее изменение энтропии может быть найдено по формуле:
|
T |
|
|
m |
|
T |
|
|
||
S C m ln |
2 |
|
|
|
C m ln |
3 |
|
, (7) |
||
|
|
|
||||||||
m |
|
|
|
T2 |
m |
|
|
|
||
|
T1 |
|
|
|
T2 |
|
|
|||
которую студентам предлагается вывести самостоятельно.
Т1 – начальная температура образца (в момент включения секундомера); Т2 – температура кристаллизации; Т3 – конечная температура образца.
Порядок выполнения работы.
1.Подсоединить установку к лабораторной сети.
2.Опустить ампулу с образцом в печь.
3.Включить тумблеры «Нагрев» и «Термометр».
4.Нагреть образец до температуры (190 – 195)ºС.
5.Выключить тумблер «Нагрев».
6.Поднять ампулу наверх, включить секундомер и фиксировать температуру образца с интервалом 5 с.
7.Получив 160 – 200 экспериментальных точек выключить секундомер, выключить тумблер «термометр» и обесточить установку. Результаты занести в таблицу.
8.Построить график Т=f(t). По нему определить скорости изменения температуры на участках 1 и 3, а также время кристаллизации Δt.
9.По формуле 6 вычислить Q , а затем по формуле 5 – удельную теплоту кристаллизации.
10.По формуле 7 определить изменение энтропии образца в процессе остывания.
Данные для вычислений:
С = 268,8 Дж/кг.К
m
C = 247,8 Дж/кг.К
m
CM = 500 Дж/кг.К m = 55 г.
M =50 г.
Контрольные вопросы.
1.Что называется удельной теплотой плавления вещества? В каких единицах она измеряется?
2.Как изменится вид кривой Т=f(t), если температура окружающей среды понизится? Почему?
3.Охарактеризуйте процесс плавления и отвердевания кристаллического вещества с точки зрения молекулярно-кинетической теории.
4.Что называется энтропией системы, и каковы ее свойства?
5.Сформулируйте второе начало термодинамики с учетом изменения энтропии при различных процессах в изолированной системе.
6.Охарактеризуйте метод определения изменения энтропии, используемый в данной работе.
7.Выведите расчетные формулы 6 и 7.
|
|
|
|
|
|
|
Таблица. |
|
t, c |
t, oC |
t, c |
t, oC |
t, c |
t, oC |
t, c |
t, oC |
|
0 |
|
235 |
|
470 |
|
705 |
|
5 |
|
240 |
|
475 |
|
710 |
|
10 |
|
245 |
|
480 |
|
715 |
|
15 |
|
250 |
|
485 |
|
720 |
|
20 |
|
255 |
|
490 |
|
725 |
|
25 |
|
260 |
|
495 |
|
730 |
|
30 |
|
265 |
|
500 |
|
735 |
|
35 |
|
270 |
|
505 |
|
740 |
|
40 |
|
275 |
|
510 |
|
745 |
|
45 |
|
280 |
|
515 |
|
750 |
|
50 |
|
285 |
|
520 |
|
755 |
|
55 |
|
290 |
|
525 |
|
760 |
|
60 |
|
295 |
|
530 |
|
765 |
|
65 |
|
300 |
|
535 |
|
770 |
|
70 |
|
305 |
|
540 |
|
775 |
|
75 |
|
310 |
|
545 |
|
780 |
|
80 |
|
315 |
|
550 |
|
785 |
|
85 |
|
320 |
|
555 |
|
790 |
|
90 |
|
325 |
|
560 |
|
795 |
|
95 |
|
330 |
|
565 |
|
800 |
|
100 |
|
335 |
|
570 |
|
805 |
|
105 |
|
340 |
|
575 |
|
810 |
|
110 |
|
345 |
|
580 |
|
815 |
|
115 |
|
350 |
|
585 |
|
820 |
|
120 |
|
355 |
|
590 |
|
825 |
|
125 |
|
360 |
|
595 |
|
830 |
|
130 |
|
365 |
|
600 |
|
835 |
|
135 |
|
370 |
|
605 |
|
840 |
|
140 |
|
375 |
|
610 |
|
845 |
|
145 |
|
380 |
|
615 |
|
850 |
|
150 |
|
385 |
|
620 |
|
855 |
|
155 |
|
390 |
|
625 |
|
860 |
|
160 |
|
395 |
|
630 |
|
865 |
|
165 |
|
400 |
|
635 |
|
870 |
|
170 |
|
405 |
|
640 |
|
875 |
|
175 |
|
410 |
|
645 |
|
880 |
|
180 |
|
415 |
|
650 |
|
885 |
|
185 |
|
420 |
|
655 |
|
890 |
|
190 |
|
425 |
|
660 |
|
895 |
|
195 |
|
430 |
|
665 |
|
900 |
|
200 |
|
435 |
|
670 |
|
905 |
|
205 |
|
440 |
|
675 |
|
910 |
|
210 |
|
445 |
|
680 |
|
915 |
|
215 |
|
450 |
|
685 |
|
920 |
|
220 |
|
455 |
|
690 |
|
925 |
|
225 |
|
460 |
|
695 |
|
930 |
|
230 |
|
465 |
|
700 |
|
935 |
|
