3.2 Физический смысл производной

Предположим, что некоторая точка движется прямолинейно, и ее путь можно описать по закону х(t). То есть за определенное время t точка пройдет расстояние х. А теперь вспомним формулу скорости:   .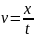

Чтобы найти среднюю скорость на каком-то участке пути точки, нужно разделить весь путь на все время, или 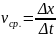. Таким образом, мы пришли к определению производной. 

Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t. x'(t) = v.

Глава 4. Применение производной в физике и химии

4.1. Применение производной в физике

1. Скорость как производная пути

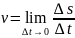
2. Ускорение как производная скорости a =

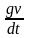
3. Скорость распада радиоактивных элементов = - λ N

А также в физике производную применяют для вычисления:

Скорости материальной точки

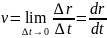
Мгновенной скорости как физический смысл производной

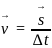
- мгновенная скорость, м/с

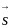- перемещение тела, м (если At-+0)

Δt - стремящийся к нулю интервал времени, с

Мгновенное значение силы переменного тока

Мгновенное значение ЭДС электромагнитной индукции

Максимальную мощность

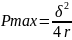
4.2 Применение производной в химии

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)

Понятие на языке химии	Обозначение	Понятие на языке математики
Количество в-ва в момент времени t0	p = p(t 0)	Функция
Интервал времени	∆t = t– t0	Приращение аргумента
Изменение количества в-ва	∆p= p(t0+ ∆ t ) – p(t0)	Приращение функции
Средняя скорость химической реакции	∆p/∆t	Отношение приращения функции к приращению аргумента

Таблица 1. – применение производной в химии

ЗАКЛЮЧЕНИЕ

Настоящая работа даёт учащимся новый подход к многим преобразованиям в математике, которые стандартным путём трудно разрешимы или разрешимы, но громоздкими способами. Рассмотренные подходы нестандартного характера для учащихся покажутся новыми и необыкновенными, что расширит их кругозор и повысит интерес к производной.

Итак, геометрический смысл производной: производная функции в точке x₀ равна угловому коэффициенту ка­сательной к графику функции, проведенной в точке с абсциссой x₀.

Физический смысл производной: произ­водная функции y = f(x) в точке x₀ - это скорость изменения функции f (х) в точке x₀

Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

Производная находит широкое приложение в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени; для нахождения наибольших и наименьших величин.

Производная является важнейшим инструментом экономического анализа, позволяющим углубить геометрический и математический смысл экономических понятий, а также выразить ряд экономических законов с помощью математических формул.

Наиболее актуально использование производной в предельном анализе, то есть при исследовании предельных величин (предельные издержки, предельная выручка, предельная производительность труда или других факторов производства и т. д.).

Производная применяется в экономической теории. Многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем

Знание производной позволяет решать многочисленные задачи по экономической теории, физике, алгебре и геометрии.