МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физики
Отчет по лабораторной работе №2
по дисциплине «Теоретические основы электротехники»
Студент гр. |
|
Преподаватель |
Константинова Е.В. |
Тема: Исследование свободных процессов в электрических цепях
Цель работы
Изучение связи между видом свободного процесса в
электрической цепи и расположением собственных частот (корней
характеристического уравнения) на комплексной плоскости; приближенная
оценка собственных частот и добротности RLC -контура по осциллограммам.
Задание
В работе предлагается исследовать свободные процессы в цепях, схемы которых представлены на рис. 1 и рис. 2.
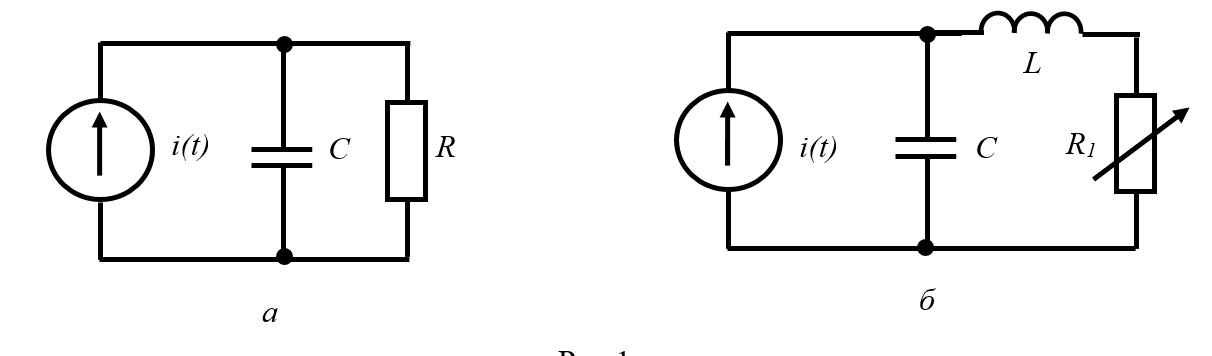
Рисунок 1. Цепи первого и второго порядка
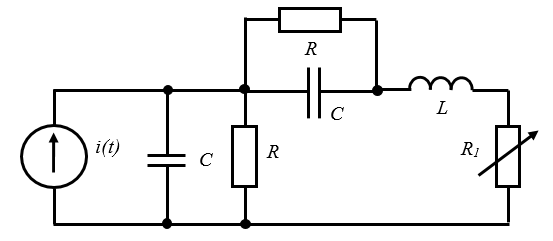
Рисунок 2. Цепь третьего порядка
Экспериментальные исследования с применением моделирующих компьютерных программных средств Multisim
1. Исследование свободного процесса в цепи первого порядка
Рисунок
3. Цепь первого порядка
помощью ключей S1,
S2
была собрана цепь, соответствующая
схеме на рис.1(а), где R
= 5000 Ом, С = 0.02*
= 20*
Ф.
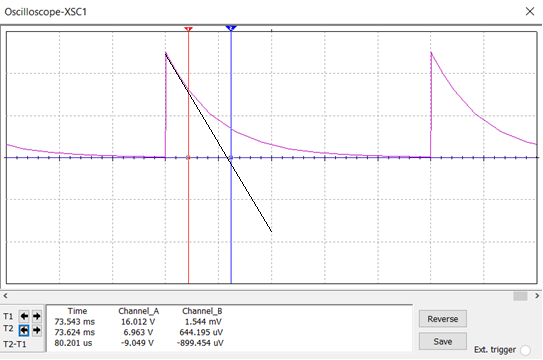
Рисунок 4. Показания осциллографа
По
методу касательной проводится касательная
из начала координат к графику (такая
касательная единственная). Считая, что
цена деления – 20*
,
делаем вывод, что касательная касается
оси х в точке ~ 115 *
с от начала координат, то есть τ
~ 1.15 *
c
Рассчитаем теоретическую собственную частоту:
p1
= -
= -1/(RC)
= -
τ =
с
Рассчитаем собственную частоту с помощью показаний осциллографа:
T = 80.201 * c (см. рис. 4)
p1
=-
=-
= -
= -10 383,013
=
= 0.963*
c
Рисунок 5. Расположение собственных частот
Вывод: практически полученные значения постоянной времени практически совпадают со значением, вычисленным теоретически, что говорит о высокой точности проделанных вычислений.
2. Исследование свободного процесса в цепи второго порядка
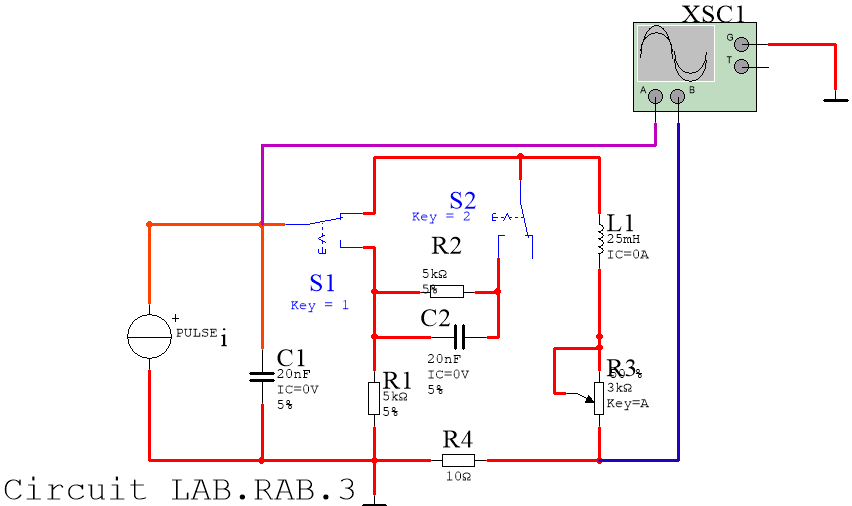
Рисунок 6. Цепь второго порядка
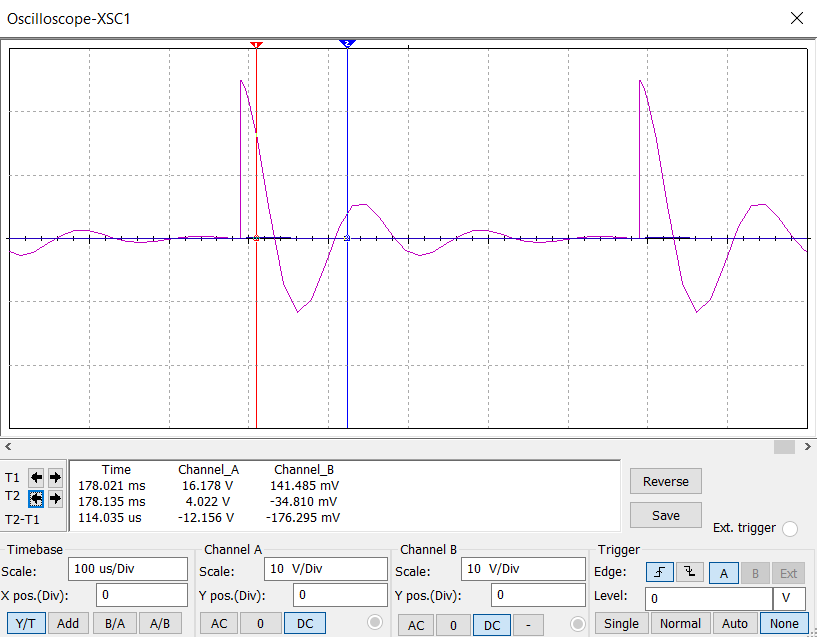
Рисунок 7. Колебательный режим
Рассчитаем теоретические параметры колебательного режима.
α
=
=
= 10000
ω0
=
=
= 44721
p1,
2 = -α
±
= -10000 ± j43588.6205
Q
=
= 2.236 > 0.5
Длительность
переходного процесса: T
= 3τ = 3
= 3 *
c
Экспериментально найденные параметры колебательного режима.
α
=
=
= 12 205,665
ω0
=
=
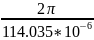= 55 098,744
Q
=
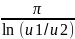= 2,257
Рисунок 8. Для колебательного режима
Вывод: практически полученные значения практически совпадают со
значением, вычисленным теоретически, что говорит о высокой точности
проделанных вычислений.
Рисунок 9. Апериодический режим
Рассчитаем теоретические параметры апериодического режима.
α
=
=
= 60000
ω0 = = = 44721
p1, 2 = -α ± = -60000 ± 40000
p1 = -20000, p2 = -100000
Q = = 0.37 < 0.5
Длительность
переходного процесса: T
= 3τ = 3
= 5 *
с
Рисунок 10. Для апериодического режима
Рисунок 11. Критический режим
Определим сопротивление R3, при котором соблюдается критический режим (то есть Q = 0.5)
R3[крит] = 2.235 кОм (74, 5%, точнее было бы 74.535%, но такие деления отсутствуют)
Рассчитаем теоретические параметры критического режима цепи:
α
=
=
= 44700
ω0 = = = 44721 ~ α
p1, 2 = -α ± ~ -44700 ± 0
Q = ~ 0.5 чтд
Длительность
переходного процесса 𝑇
= 3𝜏
=
= 0.67 *
c
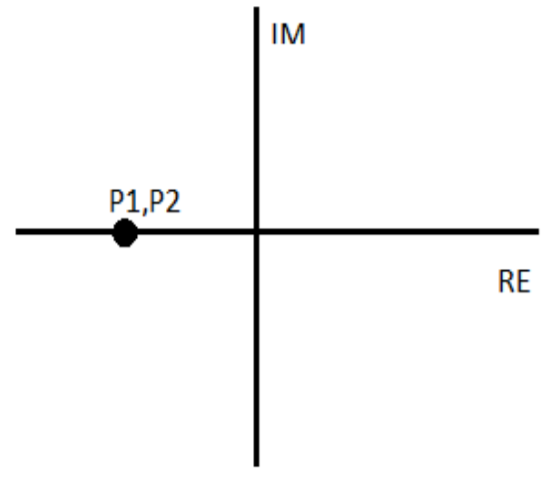
Рисунок 12. Для критического режима
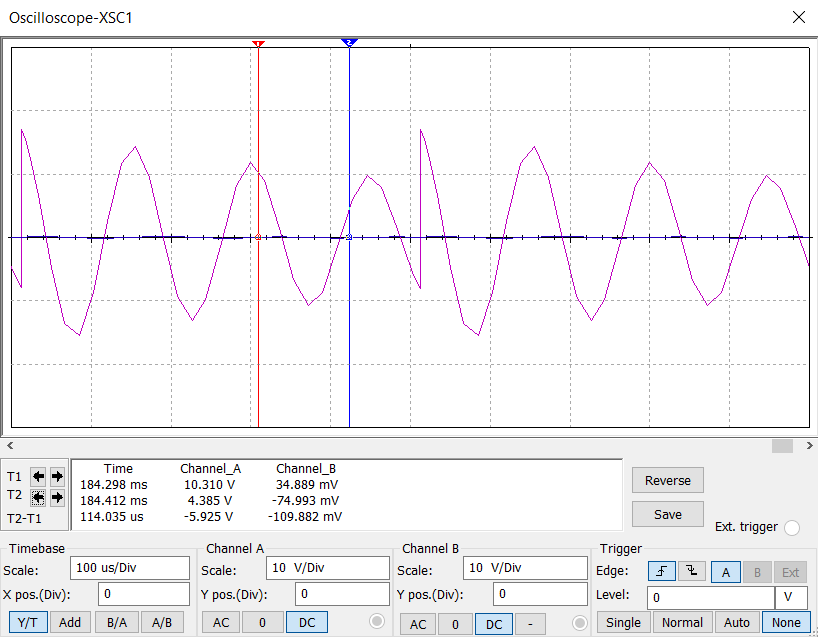
Рисунок 13. Цепь с высокой добротностью
Рассчитаем теоретические параметры цепи при высокой добротности:
α
=
=
= 600
ω0 = = = 44721
p1, 2 = -α ± = -600 ± j44716
Q = =37.2675
Длительность переходного процесса: T = 3τ = 3 = 0.005 c
Рисунок 14. Для цепи с высокой добротностью
2. Исследование свободного процесса в цепи третьего порядка
C = С1 = С2 = 0.02 мкФ, R1 = 𝑅2 = 5 кОм, R3 = 1 кОм, L = 25 мГн
Рисунок 15. Цепь третьего порядка
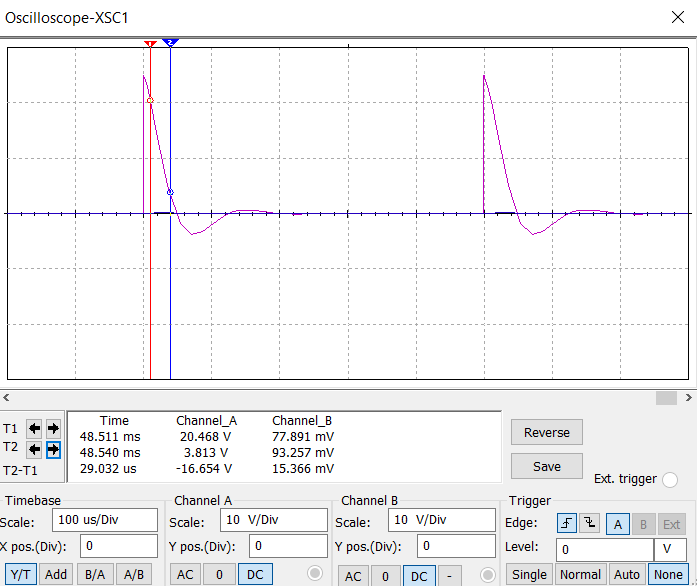
Рисунок 16. Цепь третьего порядка
Рассчитаем теоретически частоты собственных колебаний цепи
p1
= -
= -10000
=
(
+
)
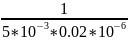= 25000
=
-25000
±
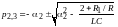= -25000 ± j61441
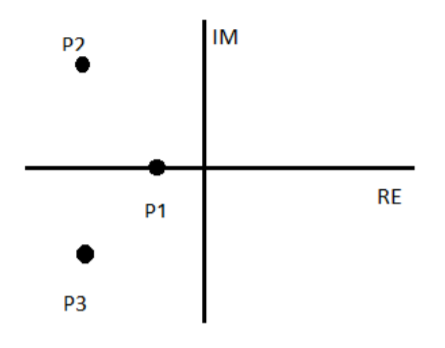
Рисунок 17. Расположение собственных частот
Вывод
В ходе выполнения лабораторной работы было проверено, что форма реакции цепи зависит от вида собственных частот: в случае если собственные частоты вещественные, то в цепи наблюдается апериодический режим, комплексно-сопряженные – периодический режим, кратные – критический апериодический режим.
Несовпадение теоретических и экспериментальных данных вызвано также неточностью измерений и неточностью номиналов элементов.
Санкт-Петербург
2021