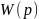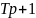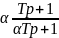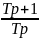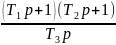Тау 6 семестр / лр 2 / Федоров лр2------------------------5-

Нижегородский Государственный Технический Университет

Имени Р.Е.Алексеева

Кафедра “Электрооборудование, электропривод и автоматика”

Отчет по лабораторной работе №2

“ Характеристики типовых корректирующих устройств”

Выполнил:

Федоров К.Р.

Проверил:

Мельников В.Л.

Нижний Новгород

2022 г.

Цель: теоретическое и экспериментальное определение и исследование характеристики типовых корректирующих устройств.

Программа работы:

1. Получить выражения передаточных функций корректирующих устройств при различных вариантах реализации.

2. Получить аналитические выражения переходных и частотных характеристик.

3. Разработать модели КУ в среде SamSim. Получить графики переходных и частотных характеристик (

4. С использованием модели в среде SamSim исследовать влияние гибкой обратной связи на переходные процессы колебательного звена.

Тип		Вар	5
ПД		Т	0.13
		α	0.1
ПИ		Т,Т1	0.13
		Т2	0.013
ПИД		Т1	0.13
		Т2	0.013
		Т3	0.13

Варианты исходных данных:

1.1

Тип – пропорционально-дифференциальное корректирующее устройство

Передаточная функция:

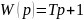
1.2

Переходная характеристика:

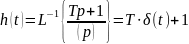
Частотные характеристики:

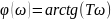
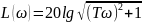
1.3

Модель, выполненная в SamSim:

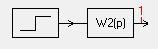
График переходной характеристики:

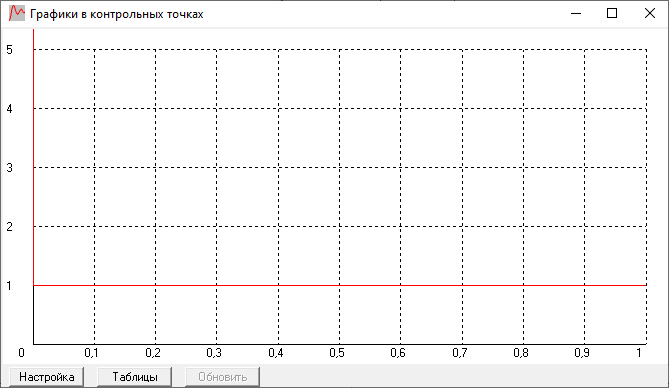
Годограф:

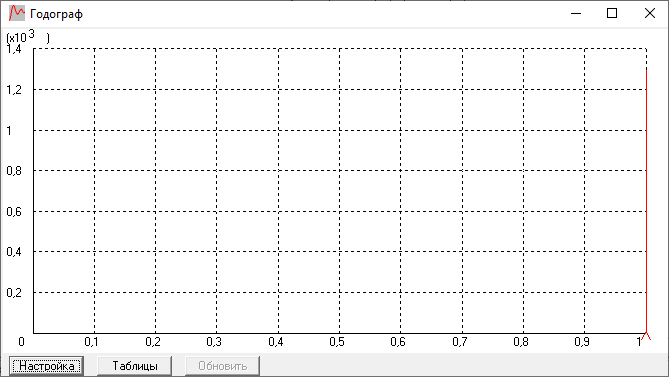
ЛАЧХ и ЛФЧХ:

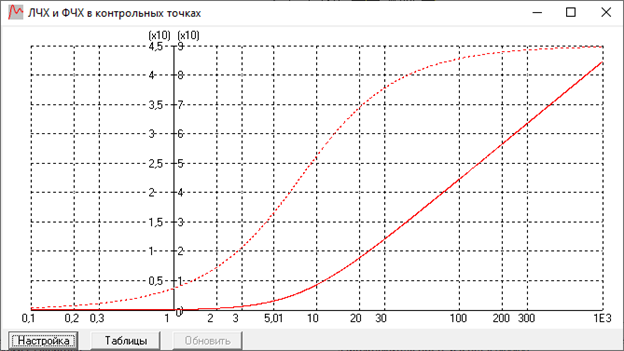
Вывод: рассчитанная переходная характеристика совпадает с полученной экспериментально. ЛАЧХ совпадает с осью на низких частотах, и имеет наклон +20 дб/дек при 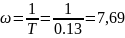. Годограф также соответствует ожидаемым результатам, берет начало из точки +1, и идет перпендикулярно вверх, из-за форсирующего звена.

2.1

Тип – пропорционально-дифференциальное корректирующее устройство

Передаточная функция:

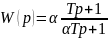
2.2

Переходная характеристика:

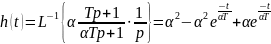
Частотные характеристики:

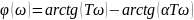
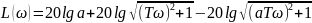
2.3

Модель, выполненная в SamSim:

График переходной характеристики:

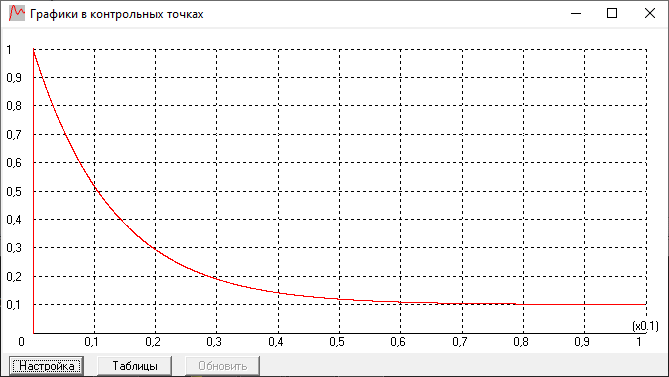
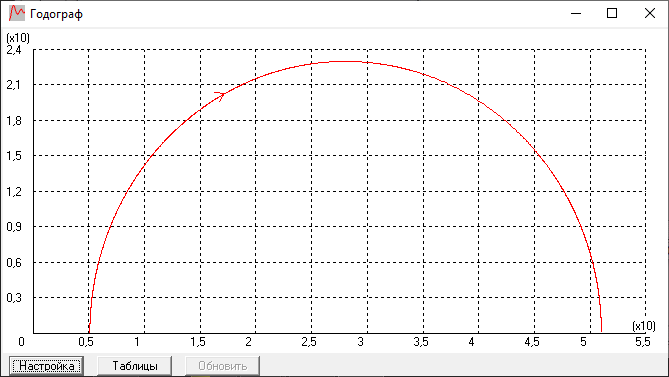
Годограф:

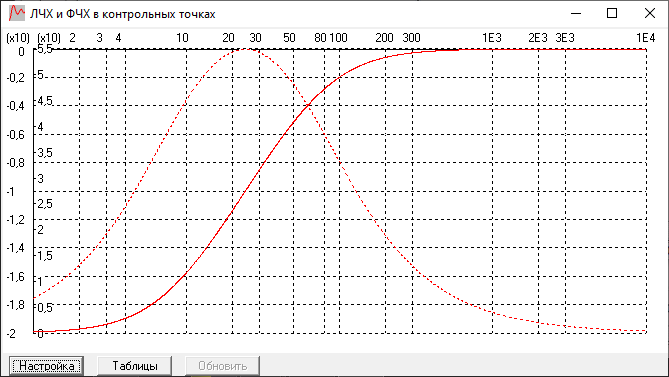
ЛАЧХ и ЛФЧХ:

Вывод: рассчитанная переходная характеристика совпадает с полученной экспериментально. ЛАЧХ берет начало из точки 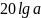, и имеет наклон +20 дб/дек при а затем 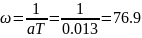имеет наклон 0 дб/дек. Годограф также соответствует ожидаемым результатам, имеет форму полуокружности из-за последовательно соединённых инерционного и форсирующего звеньев, причем T форсирующего > T иннерционного.

3.1

Тип – пропорционально-интегральное корректирующее устройство

Передаточная функция:

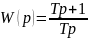
3.2

Переходная характеристика:

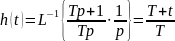
Частотные характеристики:

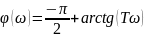
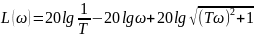
3.3

Модель, выполненная в SamSim:

График переходной характеристики:

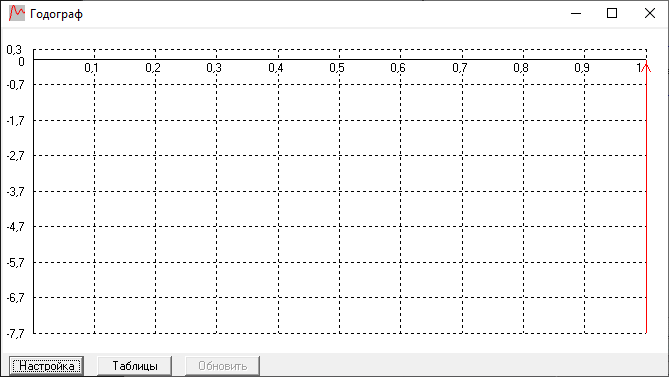
Годограф:

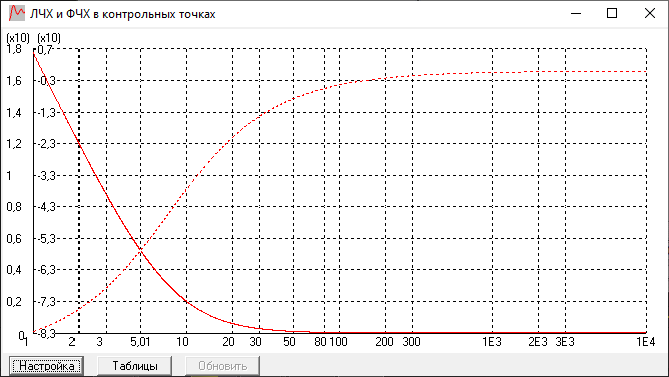
ЛАЧХ и ЛФЧХ:

Вывод: рассчитанная переходная характеристика совпадает с полученной экспериментально. ЛАЧХ берет начало из точки 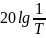, и имеет наклон -20 дб/дек на низких частотах, а затем при имеет наклон 0 дб/дек. Годограф также соответствует ожидаемым результатам, берет начало в IV четверти координатной плоскости, и идет перпендикулярно вверх, из-за форсирующего звена, к точке +1.

4.1

Тип – пропорционально-интегральное корректирующее устройство

Передаточная функция:

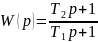
4.2

Переходная характеристика:

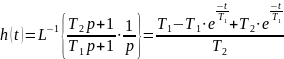
Частотные характеристики:

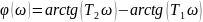
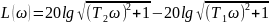
4.3

Модель, выполненная в SamSim:

График переходной характеристики:

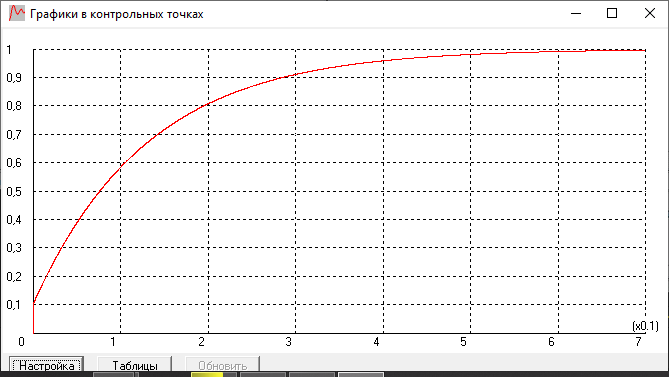
Годограф:

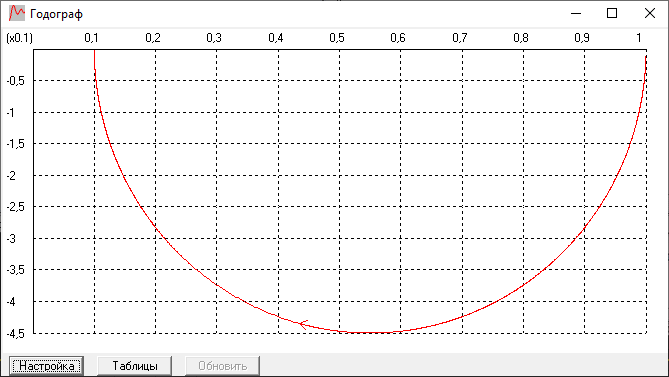
ЛАЧХ и ЛФЧХ:

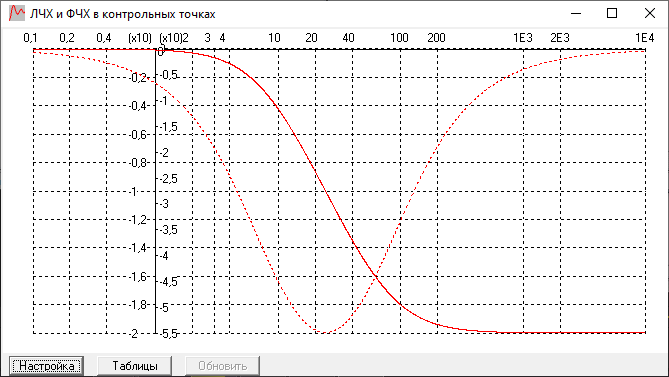
Вывод: рассчитанная переходная характеристика совпадает с полученной экспериментально. Изначально ЛАЧХ совпадает с осью, затем имеет наклон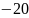 дб/дек при 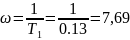а после при 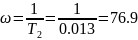имеет наклон 0 дб/дек. Годограф также соответствует ожидаемым результатам, имеет форму полуокружности из-за последовательно соединённых инерционного и форсирующего звеньев, причем T инерционного > T форсирующего.

5.1

Тип – пропорционально-интегрально-дифференциальный регулятор

Передаточная функция:

5.2

Переходная характеристика:

Частотные характеристики:

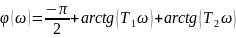
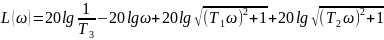
5.3

Модель, выполненная в SamSim:

График переходной характеристики:

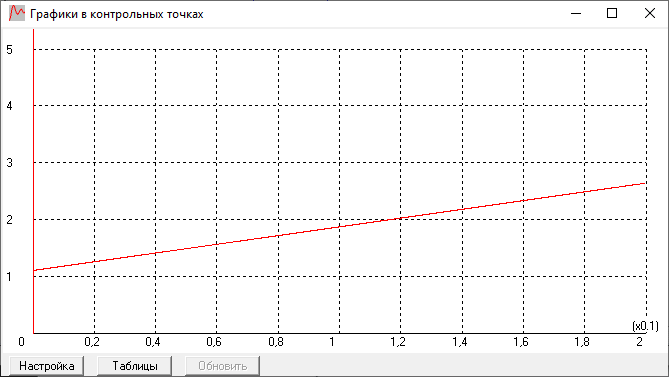
Годограф:

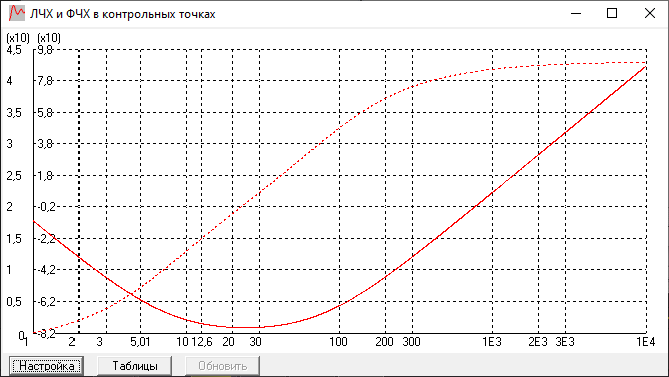
ЛАЧХ и ЛФЧХ:

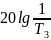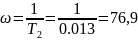Вывод: рассчитанная переходная характеристика совпадает с полученной экспериментально. ЛАЧХ берет начало из точки , и имеет наклон -20 дб/дек на низких частотах, а затем при имеет наклон 0 дб/дек. , а после при имеет наклон +20 дб/дек. Годограф также соответствует ожидаемым результатам, берет начало в IV четверти координатной плоскости, и идет перпендикулярно вверх, из-за форсирующего звена, к точке +1. И из-за второго форсирующего звена поднимается выше в I четверть.

6.

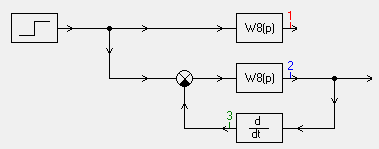
Исследование влияния гибкой обратной связи на переходные процессы колебательного звена.

Возьмем колебательное звено второго порядка с передаточной функцией:

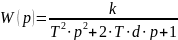
С параметрами: k = 1 ; T = 0.1 ; d = 0.25

А также дифференцирующее звено в цепи обратной связи:

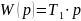
Модель, выполненная в SamSim:

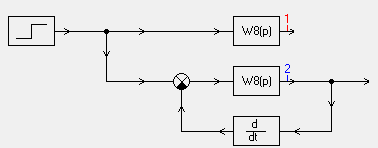
При T₁ = 0.1 имеем график:

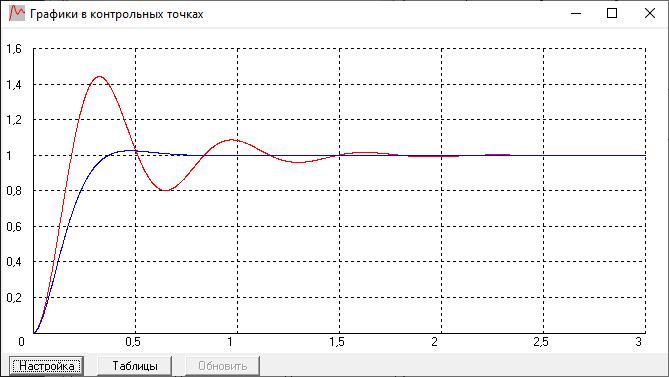
При T₁ = 0.05 имеем график:

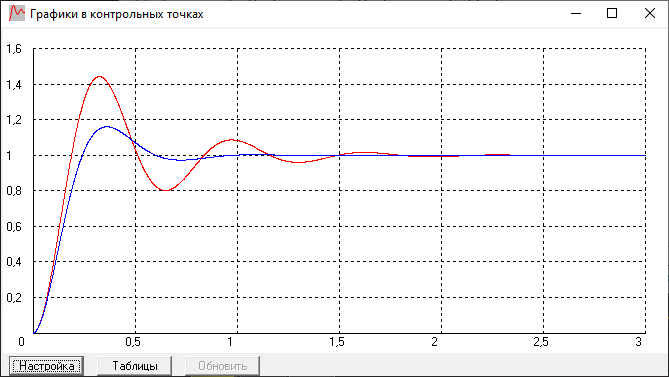
При T₁ = 0.2 имеем график:

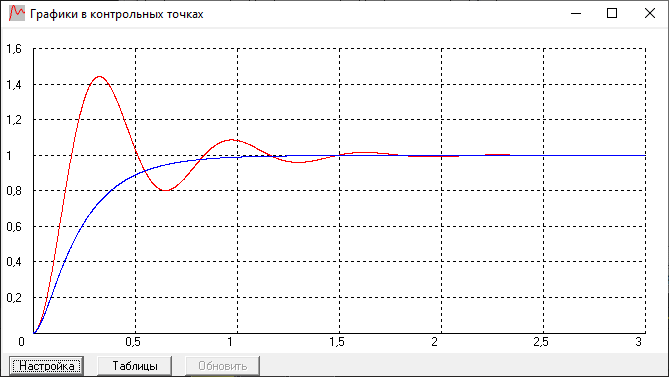
Вывод:

Оптимальный коэффициент для дифференцирующего звена в цепи обратной связи это T₁ = 0,1 так как при меньшем значении T₁ колебания составляют больше чем 4% от величины входного сигнала, а при большем значении T₁ мы получаем «вялый» график, который слишком медленно приходит к установившемуся значению.