
Раздел V. Атомная и ядерная физика. Глава 3. Простейшие задачи квантовой механики.
1.Туннельный эффект.
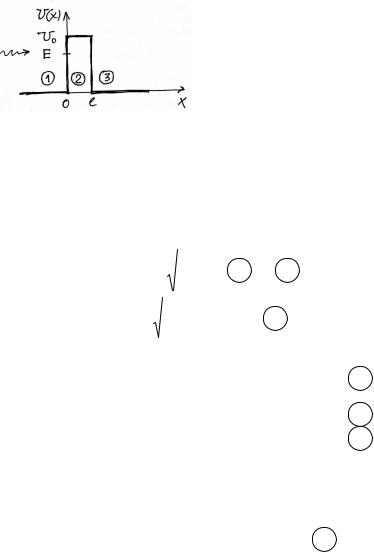
Частица движется на потенциальный барьер слева, энергия частицы меньше высоты потенциального барьера
EU0 .
Сточки зрения классической механики, такая частица не может пройти через барьер. В квантовой механике появляется отличная от 0 вероятность прохождения через барьер.
Стационарное уравнение Шредингера в соответствующих областях имеет вид:
|
d 2 |
2 |
|
|
|
|
2mE |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
, |
|
|
|
|
1 |
и 3 |
|
|||||
|
dx |
2 |
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
d |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
2m U0 E |
|
|
|||||||||||
|
|
|
0 , |
|
|
|
|
|
|
|
|
2 |
|
||||||
|
dx2 |
|
|
|
|
|
2 |
|
|
|
|
||||||||
Решения в соответствующих областях: |
|
||||||||||||||||||
|
1 |
(x) A ei x B |
e i x |
|
|
|
x<0 |
1 |
|||||||||||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||||
2 ( x) A2 e x |
B2e x |
|
|
|
0 x |
2 |
|||||||||||||
3 (x) A3ei x |
B3 i x |
|
|
|
x |
3 |
|||||||||||||
A1 - амплитуда падающей на барьер волны
B1 - амплитуда отраженной от барьера волны
A3 - амплитуда прошедшей через барьер волны
B3 0, так как отраженной волны в области 3 нет.
Волновая функция и ее производная обязаны быть непрерывными:
1(0) 2 (0) A1 B1 A2 B2
2 ( ) 3 ( ) A2 e B2 e A3ei
1'(0) 2 '(0) i A1 i B1 A2 B2
2 '( ) 3 '( ) A2 e B2 e i A3 e i
Из этих уравнений коэффициент прохождения

D |
| A |2 |
получается следующим: |
|||||||||
3 |
|
||||||||||
| A |2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
D D0e |
|
2m(U0 |
E) |
D0 |
~1 |
||||||
|
|||||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Если потенциальный барьер не прямоугольный, то:
2X2
2m U(x) E dx
D D0e X1
Коэффициент прохождения тем больше, чем ниже и уже потенциальный барьер.
Туннельный эффект лежит в основе многих явлений:- распад, спонтанное деление ядер, контактная разность потенциалов, холодная эмиссия электронов из металлов…
2.Квантование энергии частицы в потенциальной яме.
|
|
|
|
|
|
При 0<x<a стационарное |
||||||||||||||||
|
|
|
|
|
|
уравнение Шредингера: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
d2 (x) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E (x) |
|||||
|
2m |
dx2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
d |
|
2 0, |
|||||||||||||
|
|
|
|
|
|
|
dx2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2mE |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
Граничные условия: (0) 0, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(a) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Общий вид решения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) Csin( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
En |
|
|
2 2 |
|
|
n2 |
|
|||||||||
(0) 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2m |
|
a |
2 |
|
|
|
||||||||
(a) 0 a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n=1, 2, 3… |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Csin |
nx |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если нормировать волновые функции условием |
||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |2 dx 1, то C |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия частицы в потенциальной яме не может быть произвольной, а только из набора дискретных значений En . Этот эффект называется эффектом квантования. В
квантовой механике не только энергия, но и другие физические величины могут быть дискретными.

3.Эффект вырождения по энергии.
В трехмерном потенциальном ящике (U 0 внутри ящика, U вне)
энергия частицы и соответствующие волновые функции имеют вид:
|
|
2 |
n |
|
2 |
|
n |
|
2 |
|
n |
|
2 |
|
|
En1n2n3 |
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|||
2m |
|
a |
2 |
b |
2 |
c |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
n n n |
|
8 |
sin |
n1 x |
sin |
n2 y |
sin |
n3 z |
|
abc |
|
|
c |
||||||
1 |
2 |
3 |
|
a |
b |
||||
|
|
|
|
|
|
|
|||
n1,n2 ,n3 1, 2, 3…
При a=b=c вследствие симметрии U(x,y,z)
E112 E121 E211
E123 E321 E231 и т.д.
Явление, когда частица описывается различными волновыми функциями (различные квантовые состояния), а энергии одинаковы, называется эффектом вырождения по энергии. Это явление связано с симметрией потенциальной энергии частицы.
Вопросы.
1.Что такое туннельный эффект.
2.Что такое квантование энергии.
3.Что такое вырождение по энергии.
4.Спектр энергий частицы в потенциальной яме и ящике.
