§32. Расстояние от точки до прямой на плоскости

Для этого проведём прямую , проходящую через заданную точку и перпендикулярную заданной прямой . Пусть - точка пересечения прямых и . Тогда расстояние от точки до прямой совпадает с расстоянием между точками и (см. чертёж32.1).

Попутно мы решаем задачу получения уравнения прямой, проходящей через заданную точку и перпендикулярной заданной прямой.

Итак, пусть прямая задана уравнением (29.5) и – её нормаль .

Тогда , то есть получается как прямая, проходящая через точку и коллинеарная вектору . Согласно §29 (см. равенство 29.4), её уравнение имеет вид или (32.1)

Тогда - точка пересечения прямых, заданных уравнениями (29.5) и (32.1) и, по формулам (30.13) (для , и ), её координаты можно найти из уравнений:

(32.2)

рис.32.1

Тогда расстояние:

=

=

Итак, расстояние от точки M*(x*,y*) до прямой l, задаётся уравнением (29.5), можно найти по формуле:

(32.3)

ЗАДАЧА. Доказать, что координаты проекции точки M*(x*,y*) на прямую l, заданную уравнением (29.5), можно найти по формулам (32.2).

§§33 35 Кривые второго порядка

Пусть на плоскости задана прямоугольная декартова система координат.

        Определение 33.1. Линией второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка

ax2 + bxy + cy2 + dx +fy +g = 0

(33.1)

где a, b, c, d, f, g –– вещественные числа, и хотя бы одно из чисел a, b, c отлично от нуля.

Уравнение (33.1) в зависимости от коэффициентов может задавать только три типа кривых, а именно, эллипс (частным случаем которого является окружность), гиперболу и параболу. (Впрочем, могут быть также распадающиеся и вырожденные линии; более подробнее об этом в § 35).

§33 Эллипс, как кривая второго порядка. Его полуоси, эксцентриситет, фокусы и директрисы. Окружность в качестве частного случая эллипса.

33.1 Эллипс, как кривая второго порядка.

        Определение 33.2.   Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.         

Для эллипса можно дать еще несколько эквивалентных определений. Стоит отметить, что эллипс –– это кривая, получающаяся как проекция на плоскость π окружности, лежащей в плоскости, которая образует острый угол с плоскостью π.

В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат крайне сложно. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым, т.е. получаем каноническое уравнение эллипса.

Пусть F₁ и F₂ –– фокусы эллипса. Начало O системы координат расположим на середине отрезка F₁F₂. Ось O_x направим вдоль этого отрезка, ось O_y –– перпендикулярно к этому отрезку (рис. 33.1).

        Теорема 33.1. Пусть сумма расстояний от точки эллипса до фокусов равна 2a, а расстояние между фокусами –– 2c. Тогда в выбранной системе координат эллипс имеет уравнение

(33.2)

где

(33.5)

        Доказательство.     Пусть M (x; y) –– текущая точка эллипса. По определению эллипса F₁M + F₂M =2a. Из треугольника F₁MF₂ видно, что F₁M + F₂M > F₁F₂, то есть 2a > 2c, a > c, и поэтому число существует (см. рис 33.1).

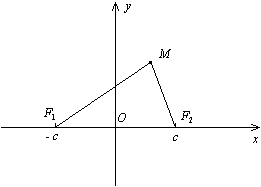
Рис. 33.1.

Ф окусами в выбранной системе координат являются точки F₁(-c; 0), F₂ (c; 0). Легко заметить, что

Тогда по определению эллипса

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что (33.5), имеем равенство

Наконец, разделив обе части на , получим уравнение 

(33.4)

Определение 33.3. Уравнение (33.4) называется каноническим уравнением эллипса.